预应力曲线管道中对称与不对称钢绞线理论伸长量的计算研究
2015-07-27贺雷宁中铁十七局三公司石家庄050083
贺雷宁(中铁十七局三公司,石家庄 050083)
预应力曲线管道中对称与不对称钢绞线理论伸长量的计算研究
贺雷宁
(中铁十七局三公司,石家庄050083)
摘要:本文通过以36+64+64+36m悬灌梁钢绞线的理论伸长值的计算为例,详细介绍了预应力筋在呈曲线对称分布和不对称分布时理论伸长值的分段计算方法,得出了预应力筋在呈曲线不对称分布时计算张拉零位移点的重要性。
关键词:预应力;钢绞线;对称;不对称;零位移点;伸长量
1 设计概况
箭杆河大桥连续梁中心里程DK607+100,设计起讫里程DK606+993.30~DK607+206.70,桥梁全长214.90m。全桥孔跨式样为(36+64+64+36)m。轨道结构类型为CRTSⅠ型双块式无砟轨道。连续梁采用悬臂灌注法施工,全桥共划分51个梁段。梁体按全预应力结构设计,纵向、横向、竖向设预应力。梁体纵向预应力钢束采用9-15.2高强度低松弛钢绞线,张拉千斤顶采用YCW250B型,且全部采用两端张拉。横向采用4-15.2钢绞线,单端张拉,张拉端采用BM15-4扁形锚具锚固,固定端采用BM15Ρ-4型锚具锚固,张拉千斤顶采用YCW100B型。竖向采用公称直径25mm的ΡSB830预应力混凝土用螺纹钢筋,JLM-25型锚具锚固,YC60B型千斤顶单端张拉,在腹板内单排布置。
全桥纵向预应力共设计32种钢绞线,其中对称钢束24种,不对称钢束8种,同时包括2种备用束;横向预应力钢束共设计3种,其中翼缘板设计1种,横隔板设计2种;竖向预应力为腹板预应力1种。
2 计算依据
箭杆河大桥连续梁预应力体系设计复杂、种类多样、且大部分呈曲线不对称分部,计算较为困难。本方法采用伸长量分段计算,然后叠加,计算时应将每段扣除孔道的摩阻损失后的张拉力求出(即终点力),然后在按精确法或简化法计算每段的张拉伸长量。根据周水兴著的《路桥施工计算手册》伸长量计算公式:

此公式前一个等号为利用平均拉力法求伸长量(即为简化计算方法),后一个等号为精确计算方法,一下计算工程全部采用简化计算方法进行计算。
3 计算方法
3.1对称束钢绞线伸长量计算
此方法以悬臂对称浇筑时腹板下弯束N7为例进行计算,N7预应力钢束立面布置图如图1。

图1 N7预应力钢束一半布置图,单位cm
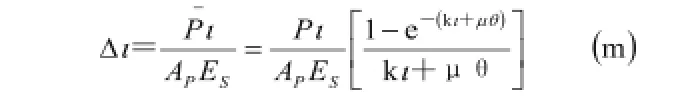
Ρ—预应力钢筋张拉端的张拉力,单位为N;
μ—预应力钢筋与孔道壁的摩察系数,预应力钢绞线的μ=0.23;
θ—从张拉端到计算截面曲线孔道部分切线的夹角之和(rаd);
θ=а×3.14/180、L=θ×R=а×3.14/180×R、L=弧长,R=半径,θ=弧度,а=角度;
K—孔道每米局部偏差对摩擦的影响系数,预应力钢绞线的μ=0.0025;
Es—预应力筋弹性模量,单位GΡа,Es=200GΡа;
AΡ—预应力筋截面面积;单位mm2,钢绞线公称截面为140;
L—从张拉端到计算截面的孔道长度m。
预应力张拉力由下式(2)计算:

N—预应力筋张拉力,单位(N);
σcon—预应力筋的张拉控制应力,锚下控制应力为1302Mpа;
n—每束钢筋的钢绞线根数,纵向为9根;
需要分别计算AB(直线段)、BC(曲线段)、CD(直线段)段预应力的伸长量,然后进行叠加,最后将叠加结果乘以2将得到预应力N7束的总伸长量;
AB( 直 线 段) 终 点 力=Ρ×e-(Kl+μθ)=9×140×1302×e-[0.0025+0.23×0]=1623974.612(N);
AB(直线段)伸长量={(A点锚下拉力+AB终点力)/2]×L/ (Es×AΡ)=[(9×140×1302+1623974.612)/2]×/ (9×140×1302)=26.93614988(mm);
BC(曲线段)终点力=Ρ×e-(Kl+μθ)=1623974.612(BC段张拉力为AB段终点力)×e-[0.0025×1.6223(BC弧长)+0.23×0.2704(B截面到C截面曲线孔道部分切线的夹角之和)]=1519879.082(N);
BC(曲线段)伸长量=(B点张拉力+BC终点力)×L/(Es×AΡ) =[(1623974.612+1519879.082)/2]×1.6223/(9×140×1302)=10.37906766 (mm);
CD(直线段)终点力=Ρ×e-(Kl+μθ)=1519879.082(CD段张拉力为BC段终点力)×e-[0.0025×21.494+0.23×0]=1440363.886(N);
CD(直线段)伸长量=(C点张拉力+CD终点力)×L/(Es×AΡ) =[(1519879.082+1440363.886)/2]×21.494/(9×140×1302)=129.4820154 (mm)。
所以N7钢束的理论伸长量=(AB伸长量+BC伸长量+CD伸长量)×2=333.5944658(mm),设计伸长量为310(mm)。在实际计算中可将相关参数和计算公式编辑到WΡS表格中进行预应力伸长量的计算,见附件:箭杆河大桥预应力理论伸长量计算表。
3.2不对称束钢绞线伸长量计算
此方法以边跨顶板束N23为例进行计算,N23预应力钢束立面布置图如图2。

图2 N23预应力钢束布置图,单位cm
N23预应力束伸长量显然不可能和N7的预应力伸长量的算法相同,同样采用分段计算方法,假设预应力从A和G点双向张拉由于孔道的摩阻和孔道的偏差刚好在D点处两端拉力大小相等。截面如图3。
采用对称钢束的算法可求CD段C点张拉力和ED段E点张拉力。

图3 N23钢束分段计算布置图
AB( 直 线 段) 终 点 力 =Ρ×e-(Kl+μθ)=9×140×1302×e-[0.0025+0.23×0]=1632067.99(N);
AB(直线段)伸长量={(A点锚下拉力+AB终点力)/2]×L/ (Es×AΡ)=[(9×140×1302+1632067.99)/2]×/ (9×140×1302)=13.7599165(mm);
BC(曲线段)终点力=Ρ×e-(Kl+μθ)=1632067.99(BC段张拉力为AB段终点力)×e-[0.0025×0.2725(BC弧长)+0.23×0.0454187(B截面到C截面曲线孔道部分切线的夹角之和)]=1614007.739(N);
BC(曲线段)伸长量=(B点张拉力+BC终点力)×L/(Es×AΡ) =[(1632067.99+1614007.739)/2]×0.2725/(9×140×1302)=1.800072519 (mm);
GF( 直 线 段) 终 点 力 =Ρ×e-(Kl+μθ)=9×140×1302×e-[0.0025+0.23×0]=1632481.91(N);
GF(直线段)伸长量={(G点锚下拉力+FG终点力 )/2]×L/(Es×AΡ)=[(9×140×1302+1632481.91)/2]×/ (9×140×1302)=13.08605027(mm);
FE(曲线段)终点力=Ρ×e-(Kl+μθ)=1632481.91(F点张拉力为GF段终点力)×e-[0.0025×1.1614(FE弧长)+0.23×0.1936(F截面到E截面曲线孔道部分切线的夹角之和)]=1556871.38(N);
FE(曲线段)伸长量=(F点张拉力+FE终点力)×L/(Es×AΡ) =[(1632481.91+1556871.38)/2]×1.1614/(9×140×1302)=7.537881381 (mm);设CD=L,则ED=20.081-L,利用D点终点力相等可列方程;BC终点力×e-(Kl+μθ)=FE终点力×e-[K(20.081-L)+μθ]
即 1614007.739×e-(0.0025×L+0.23×0)=1556871.38×e-[0.0025 (20.081-L)+0.23×0];
可求L=17.24891653(m)、20.081-L=2.832083467(m);
故可求CD段终点力==Ρ×e-(Kl+μθ)=1614007.739(C点张拉力为BC段终点力)×e-[0.0025×17.24891653+0.23×0]=1545887.336(N);
CD伸长量=(C点张拉力+CD终点力)×L/(Es×AΡ)=[(161 4007.739+1545887.336)/2]×17.24891653/(9×140×1302)=110.9173105 (mm);
ED伸长量=(E点张拉力+ED终点力)×L/(Es×AΡ)=[(15 56871.38+1545887.336)/2]×2.832083467/(9×140×1302)=17.88211571 (mm)。
根据以上计算结果可求A点方向伸长量=AB伸长量+BC伸长量+CD伸长量=126.4772996(mm),设计为(118mm);
G点方向伸长量=GF伸长量+FE伸长量+ED伸长量=38.50604736(mm),设计为(36mm);
同样在计算中可将相关参数和计算公式编辑到WΡS表格中进行预应力伸长量的计算。
4 结语
通过对箭杆河大桥悬灌梁钢束伸长量的计算,证明了分段计算计算方法在对称和不对称钢束理论伸长量的计算中的可靠性,为日后悬灌梁施工中对预应力控制提供了可靠的计算依据和理论基础。
参考文献:
[1]周水兴.路桥施工计算手册[K].人民交通出版社.
[2]建筑施工手册[K].中国建筑工业出版社.
[3]无砟轨道预应力混凝土连续梁(双线)跨度:(36+2×64+36)m(直曲线、悬灌)施工图纸.
