精密圆柱形貌重构及三维显示方法

2015-07-26郭媛媛李济顺隋新薛玉君马伟

轴承 2015年6期

郭媛媛，李济顺，，隋新，薛玉君，，马伟

（1.河南科技大学机电工程学院，河南洛阳 471003；2.河南省机械设计及传动系统重点实验室，河南洛阳 471003）

高档数控机床对轴承均有高速、高精度的要求，轴承的精度检测是技术难点之一。对于轴承内、外圈等零件，尤其在超精密的场合，圆柱形貌误差是重要的指标。特别是基于误差分离的圆度、圆柱度形状误差，其研究及应用备受国内外重视。圆柱度形状误差测量和分离的最终目的是对被测零件的圆柱度做出正确评判，同时得出被测零件的真实轮廓形貌，便于在线补偿加工的实施［1］。基于此，有必要对圆柱度形状误差的诸要素进行适当的重构，从而得出零件的具体形貌，然后利用相关计算机图形软件实现圆柱形貌的三维显示。

在圆柱形貌重构和三维显示的技术领域，文献［2］建立了重构基准模型，并简单介绍了基于OpenGL的圆柱度形状误差三维显示的相关参数以及绘制过程［3］，完成了圆柱度形状误差的网格状构建，但其只取得了一定的显示效果，并不是非常直观。与此同时，在科技研究中，数据场的可视化问题也越来越受到重视，选择好的渐变颜色表达和区分不同的、可见或不可见的数据场，对人视觉系统的分辨和识别极其有利［4］。因此，重点研究了精密圆柱形貌重构模型和三维显示模型，利用图形显示软件OpenGL图形库的强大功能，用颜色渲染的相应算法清楚地再现了带有颜色渐变的圆柱体的表面形貌，取得了良好的显示效果，使描述和评价圆柱度误差更加准确、直观。

1 三点法圆柱度误差测量和分离方法

圆柱度误差测量一般要求2个测量运动才能完成对圆柱体表面的计量，属于二维误差分离技术。圆柱度误差测量和分离的方法目前有3种：三点法、四点法和五点法。三点法模型得到了广泛认可，四点法、五点法模型仍需进一步探讨才能付诸使用，因此选择三点法圆柱度误差测量和分离模型进行研究。

由于圆柱度误差测量和分离的困难性、复杂性，在模型中将圆柱度形状误差分解成3个要素：（1）截面圆度形状误差，反映截面轮廓的圆度误差；（2）截面的尺寸偏差或者最小二乘圆半径差，反映零件被测截面基本尺寸变动量；（3）截面最小二乘圆圆心的位置，反映零件被测面在坐标系内的位置，也反映被测零件各个截面之间的相互位置关系。

测量时，同时使用3个传感器。参照三点法圆度误差分离技术，对圆柱上第j个截面的圆度误差进行时域计算，得到圆柱上该点的圆度误差值为

式中：M为被测截面个数。

若以测量的初始截面为考察标准，则各个被测截面的最小二乘圆半径差Δr（j）可表示为

式中：c0，c1，c2为误差分离权函数［1］。

由三点法圆柱度误差分离技术可知，截面最小二乘圆圆心与测量坐标系的原点重合，则可得到圆柱度形状误差测量的3个要素。

2 圆柱表面形貌重构

由上述测量和分离原理得到的圆柱度形状误差的3个要素是各自独立的，若要正确评价和描述圆柱度误差，就要对圆柱度形状误差的诸要素进行符合实际的、恰如其分的重构，从而获得能够表征被测零件逼真的表面形状的误差轮廓，即圆柱体的具体形貌［1］。

由于被测截面的圆度误差是以截面最小二乘圆圆心为基准进行描述，因此将截面的最小二乘圆圆心在绝对坐标系内的初始位置（aj，bj，wj）作为被测圆柱体形貌重构的基准。

各截面的圆度误差只是反应圆轮廓的变化量，故在重构时，各个截面的圆度误差需要加上常量C，使重构的圆柱体形貌更加逼真，而该常量只是改变圆柱体的半径，不影响对圆柱度的评定。由坐标平移定理可知，被测截面上点的坐标在绝对坐标系内的坐标为

式中：u（i，j），v（i，j），w（i，j）分别为重构点在绝对坐标系Oxyz下的坐标；（ai，bj）为第j号截面的最小二乘圆圆心坐标；H为圆柱的高。

综上，圆柱表面形状误差的重构已经完成，（5）式中重构的被测圆柱体形貌的所有点的坐标值，几乎可认为是圆柱体上各测点的真值，根据这些点的坐标值，就能容易地描述被测精密圆柱体的形貌。

3 圆柱形貌的三维显示

OpenGL是一个性能卓越的三维图形标准，提供了大量的预封装函数，其丰富的图形功能为三维图形的生成与显示提供了便利。在C＋＋Builder环境下实现圆柱表面形貌的三维显示，程序流程如图1所示。该程序的关键是彩色面的渲染以及用彩色区分圆柱表面的特征。

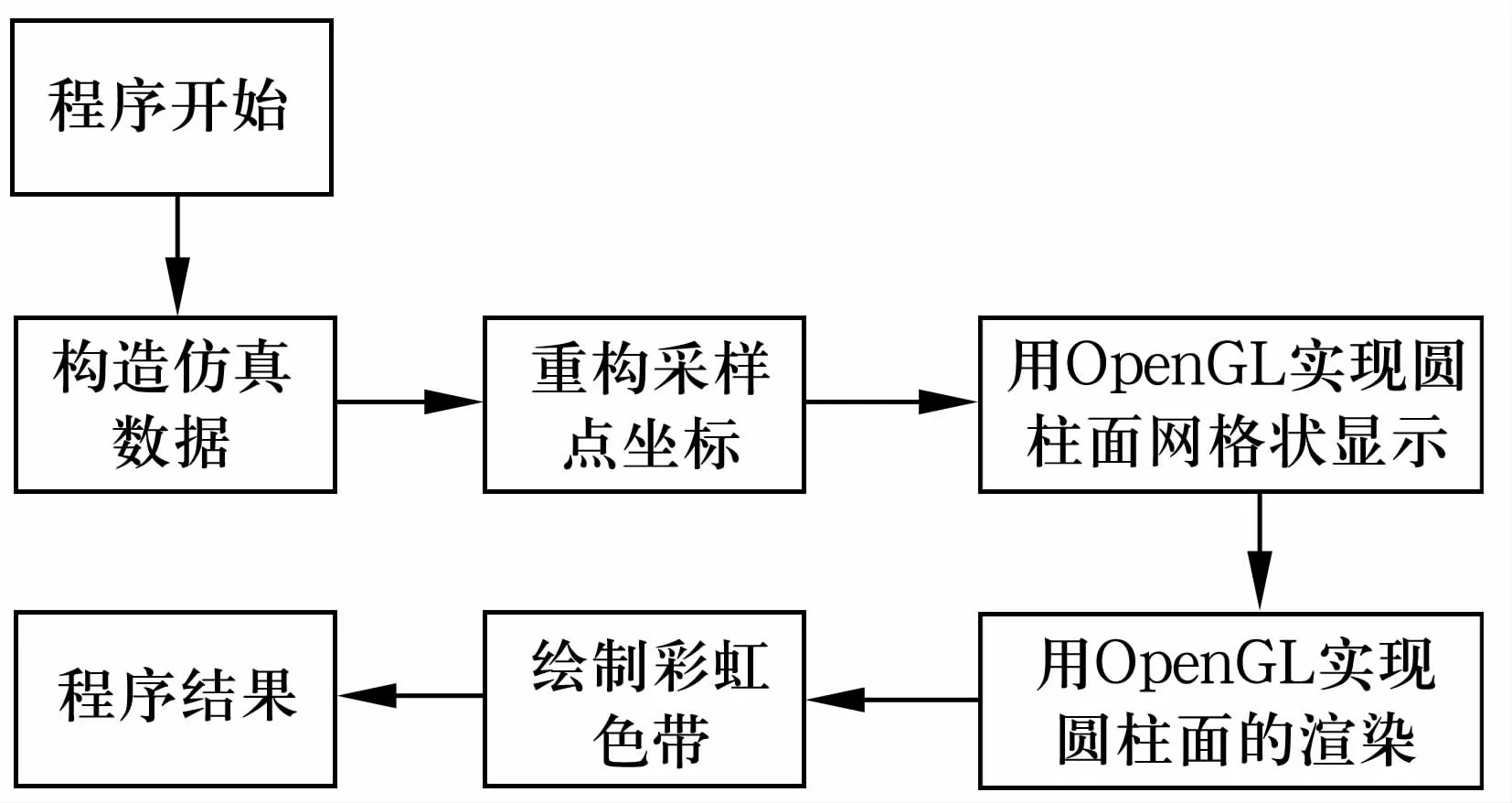
图1 圆柱表面形貌误差重构流程图

3.1 圆柱形貌空间网格的绘制

在绘制圆柱形貌之前，需要构造仿真数据。三点法圆柱度误差测量试验能够得出的测量数据是3个传感器对每个面的采样输出值，然后分离计算出每个截面的圆度误差值，最小二乘圆圆心坐标和半径差，并根据（5）式重构圆柱表面点的坐标。由于直接给出3个传感器输出的信号值相对复杂，直接给出重构所需的截面圆度误差值、截面之间半径差值、测量截面数及每个截面的采样点数，最小二乘圆圆心可根据（2）式求得，具体给定值及公式见表1。

表1 相关测量参数的给定值

为了清楚地描述圆柱面的渲染并与渲染后的圆柱面作对比，首先生成近似圆柱形貌的空间网格。具体方法如下：

根据重构点的坐标公式，实现点在空间直角坐标系下的坐标，然后以这些点的坐标为基础进行空间网格的绘制。绘制过程为：

（1）连接M个由N个点组成的空间圆线。选择OpenGL中的GL_LINE_LOOP绘制语句，该语句表明绘制闭合的直线段［6］。

（2）绘制N条由M个采样圆面对应点构成的线段。由于线段不需要闭合，所以连接直线段的函数使用OpenGL中的GL_LINE_STRIP绘制函数［6］。

在分别连接了M个圆面和上下相互对应的N条圆柱素线之后，就完成了圆柱面的空间网格的绘制。其显示结果如图2所示。

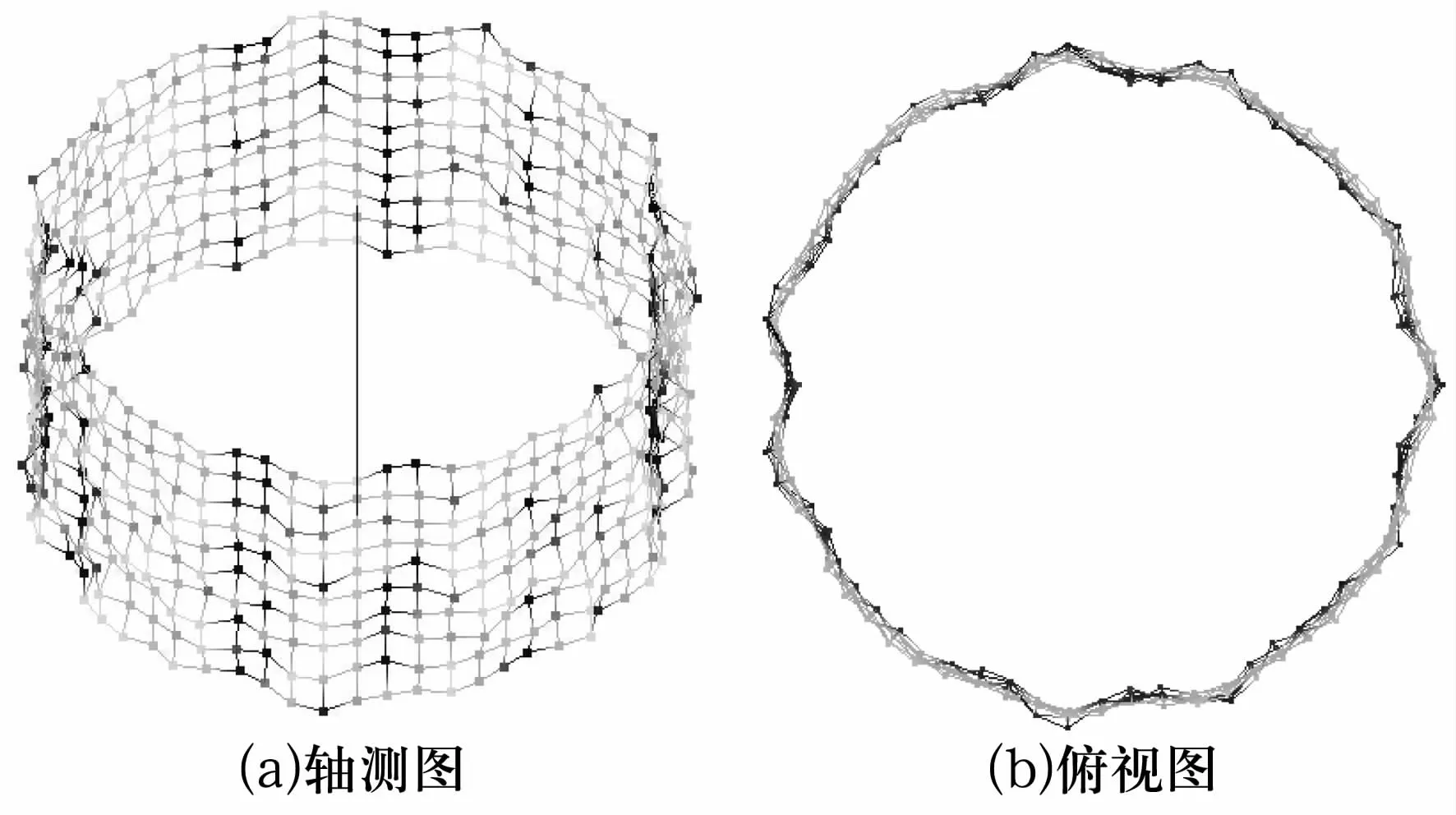
图2 圆柱形貌的空间网格

3.2 空间圆柱面的渲染

为了清楚地描述对圆柱形貌的网格状表面的渲染过程，截取圆柱形貌上的3个面，如图3所示。

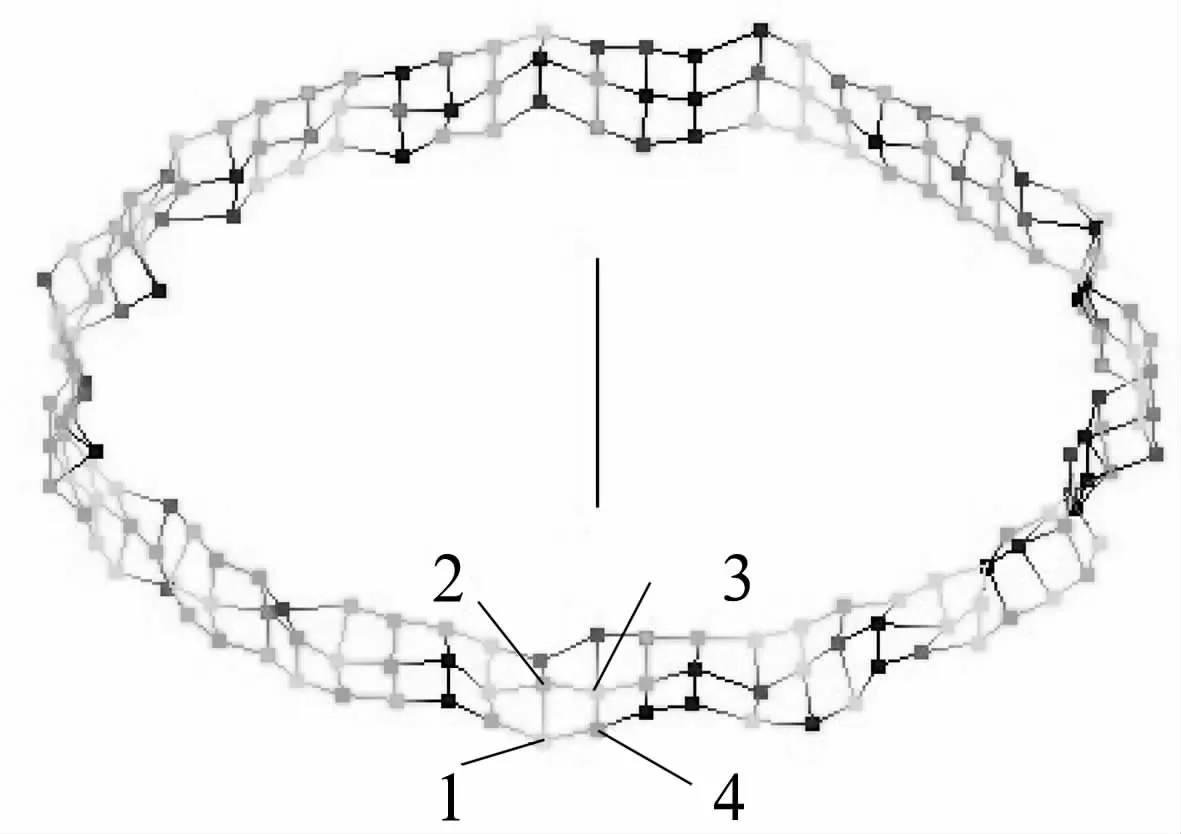
图3 圆柱形貌的空间网格片段

在将空间网格转化成面的渲染过程中，其具体实现步骤为：

（1）分别连接4个点使之成为由点1，2，3和点1，3，4组成的2个三角形面。在OpenGL函数库中的GL_TRIANGLE_STRIP语句下，用glVertex3f（）函数分别给出点1～4在直角坐标系下的坐标即可实现。

（2）嵌套C语言中的2个for循环语句就可以实现整个圆柱面上M×N个点的连接。

在连接了圆柱上所有点后，圆柱空间网格就转化成了空间圆柱面。但是，上述绘制过程实现的圆柱面是没有渐变颜色的。为了实现圆柱面的颜色渐变，需要了解OpenGL的颜色系统。在OpenGL中颜色系统采用RGB模式，该模式中每种颜色分量都是0～255，为了检索和存储方便，把这些整数换算成0.0～1.0之间的浮点数。使用的颜色函数为glColor3f（）。

要实现的圆柱表面颜色依据到圆柱中心线的距离远近依次渐变为：红色-黄色-绿色-青色-蓝色-紫色，距离最远呈红色，距离最近呈紫色。具体实现过程为：

（1）计算M×N个采样点到圆柱中心轴线的距离Distance［M］［N］，并且记下这些点到圆柱中心轴线的距离中最近和最远距离，用max和min表示。

（2）将max-min的值均分成5个区间段，即：［0，（max-min）／5］，［（max-min）／5，2（maxmin）／5］，［2（max-min）／5，3（max-min）／5］，［3（max-min）／5，4（max-min）／5］及［4（maxmin）／5，max-min］。

（3）判断Distance-min的值分别属于哪一段区间，从小到大每段对应的颜色渐变分别是紫到蓝渐变、蓝到青渐变、青到绿渐变、绿到黄渐变和黄到红渐变。然后根据颜色渐变的线性插值法，给每个点赋予相应颜色。

其中，判断点具体应该进行何种渐变的流程如图4所示。距离差指的是Distance-min，区间1～4分别是［0，（max-min）／5］，［（max-min）／5，2（max-min）／5］，［2（max-min）／5，3（maxmin）／5］和［3（max-min）／5，4（max-min）／5］。

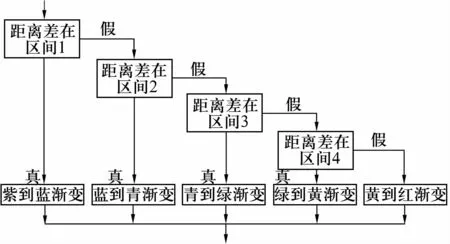
图4 圆柱表面上的点实现彩色渐变的流程

以紫到蓝渐变为例，判定若Distance的值在区间［0，（max-min）／5］中，则进行紫到蓝渐变。对应颜色渐变的线性插值法，Distance-min的最大高程值是（max-min）／5，对应的颜色是蓝色gl-Color3f（0.0，0.0，1.0），Distance-min的最小高程值是0，对应的颜色是紫色glColor3f（1.0，0.0，1.0），则区间内其他点的颜色就是glColor3f（1-（Distance-min）／（（max-min）／5），0.0，1.0）。同理，可以根据线性插值法对属于每个区间段的点进行相应的颜色渐变。由此，圆柱上每一个点的颜色由于到中心轴线的距离不同，所显示的颜色也不一样的。

在绘制圆柱表面时，将给每个点赋予颜色的程序段放在OpenGL函数库中绘制三角面片的语句GL_TRIANGLE_STRIP后面的每个glVertex3f（）语句前，即可实现带有颜色渐变的圆柱面渲染。

为了更加清晰直观地表征圆柱表面形貌，在渲染的圆柱表面绘制图中，同时绘制出彩虹色带。彩虹色带是用OpenGL函数直接绘制的带有渐变色的带状图形，圆柱表面上各个测量点的颜色与彩虹色带中的颜色源于同一个色彩空间，并且一一对应。带有彩虹带和颜色渲染的圆柱表面的显示效果如图5所示。