适于高超声速飞行器的三维非线性滑模制导律

2015-07-26彭双春朱建文汤国建陈克俊

系统工程与电子技术 2015年9期

关键词：超声速视线制导

彭双春，朱建文，汤国建，陈克俊

（国防科学技术大学航天科学与工程学院，湖南长沙410073）

适于高超声速飞行器的三维非线性滑模制导律

彭双春，朱建文，汤国建，陈克俊

（国防科学技术大学航天科学与工程学院，湖南长沙410073）

综合考虑高超声速飞行器末制导过程中的运动耦合和参数扰动问题，设计了一种适于高超声速飞行器的三维非线性伪最优滑模制导律。首先，针对运动耦合问题，定义视线旋量和视线旋量速度，构建了基于视线旋量和视线旋量速度的高超声速飞行器三维非线性制导参考模型；然后，针对参数扰动问题，基于变结构控制理论，推导出一种适于多约束制导要求的三维非线性滑模制导律，并通过理论推导证明了该制导律的稳定性；最后，引入伪控制变量，完成了制导参数的优化，从而完成三维非线性伪最优滑模制导律的设计。该制导律能够从理论上克服运动耦合和参数扰动问题，其制导参数又满足一定物理意义下的最优性。仿真结果验证了制导律的有效性。

高超声速飞行器；伪最优滑模制导律；旋量方法；运动耦合；参数扰动

0 引言

高超声速飞行器采用倾侧转弯（bank-to-turn，BTT）控制方式在三维空间中高速飞行，倾侧转弯控制方式使得飞行器－目标视线的俯仰、转弯通道存在运动耦合问题。在现有大多数制导律的推导过程中，一般都假设飞行器控制系统是稳定的，即飞行器的姿控系统使得飞行器稳定，视线的俯仰和偏航通道相互解耦，忽略了运动耦合对制导方法研究的影响，这将会造成较大的制导误差［1］。因此，如何恰当地描述飞行器目标视线通道间的运动耦合，构建合理的制导模型，是保证高超声速飞行器能够稳定飞行并最终实现对目标精确打击的基础。

同时，在高超声速飞行器末制导目标的过程中，其制导控制系统将会面临参数扰动问题［2］，如：风、温度、气流、空气动力等环境因素变化引起的参数扰动，导航制导系统观测噪声与估计误差，信号传输噪声等。此外，由于某些敌高价值慢速移动目标（如：航母、导弹发射车等）是高超声速飞行器的重点攻击对象，需要对其进行“点穴式”打击，所以在末制导过程中，需要考虑目标运动对其末制导的影响。事实上，目标运动亦可当作未知有界扰动来处理［23］。参数扰动问题使得制导系统参数存在不确定性，最终影响高超声速飞行器末制导效果。因此，需要在构建包含运动耦合模型的基础上，研究具有较强鲁棒性的制导算法，克服由于参数扰动和目标运动导致制导性能恶化的问题。

针对参数扰动问题，基于滑模变结构控制理论研究飞行器鲁棒制导问题是一种较常见的方法。近些年来取得了丰硕的研究成果：文献［4］针对空空导弹目标拦截问题，研究了变结构制导律设计问题。文献［5-8］基于平面线性制导模型，基于变结构理论开展研究，设计了最优滑模制导律和自适应滑模制导律。文献［1，3，9-10］针对导弹制导的三维模型，设计了三维变结构制导律。文献［11］针对导弹制导的落角约束要求，基于变结构理论设计了几种带落角约束的平面制导律。文献［12］将模糊变结构控制引入制导律设计过程，提出了一种自适应模糊滑模制导律。文献［13］针对有脉冲推力机动飞行器制导问题，提出了一种最优滑模制导律。文献［14］基于神经网络理论，设计了一种适于拦截器的鲁棒滑模制导律。文献［3］基于李群方法研究了一种适合BTT导弹的三维非线性滑模制导律，遗憾的是未能完成在实际工程仿真平台上的验证。

国内外研究成果为本文工作提供了良好的基础和依据，但针对高超声速飞行器末制导问题，当前研究工作仍存在不足：如文献［3，5-13］制导模型是双通道解耦模型或二维模型，文献［4，14］难以满足终端角度约束情况，并且对于三维非线性制导模型，文献［1，3，10］未完成制导参数的优化。

考虑到本文研究对象为高超声速飞行器，其飞行速度远远超过典型的慢速移动目标，参考文献［2］将慢速移动目标视作未知有界扰动，统一归纳为参数扰动问题。综合考虑高超声速飞行器末制导过程中的运动耦合和参数扰动问题，参照李群旋量结构，定义更具几何意义的视线旋量和视线旋量速度，构建关于视线旋量和视线旋量速度的高超声速飞行器三维非线性制导的参考模型，基于变结构控制理论，设计了一种适于高超声速飞行器的三维非线性滑模制导律。

1 三维非线性旋量模型

1.1 视线旋量与旋量速度

构建如图1所示的飞行器对目标进行俯冲攻击的示意图，取目标点T处的地理坐标系为目标坐标系O-xyz，目标T固定于坐标系的原点O，飞行器质心位置为M，速度为v，M′为飞行器质心M在水平面x Oz上的投影，qd和qt分别为视线高低角和视线方位角，ed和et分别为垂直于qd和qt所在平面的单位矢量，方向分别由qd和qt的符号确定，图示为qd和qt均为正的情况。

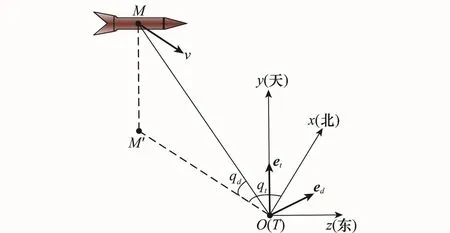
图1 飞行器对目标进行俯冲攻击示意图

定义视线旋量为

定义视线旋量速度为视线旋量的导数，记为~ω，则

~ω＝ˆ.σ （2）

从定义可以看出，视线旋量和视线旋量速度具有明确的物理意义，其三维矢量描述形式将降低制导模型构建的复杂度，便于构建飞行器制导的三维非线性参考模型。

1.2 旋量模型构建

旋量模型构建包括两方面：一是构建视线旋量变化模型，二是构建视线旋量速度变化模型。视线旋量变化模型可直接由式（2）给出，因此，旋量模型构建的关键是构建视线旋量速度变化模型。

对式（1）求二阶导数并结合式（2）可得

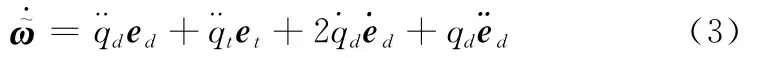
根据文献［15-16］，易知

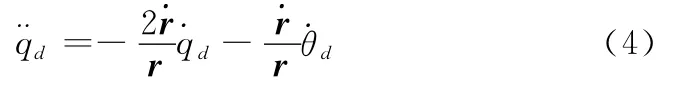
式中，r为飞行器目标视线距；θd为速度矢量在俯冲平面内的方向角。

令r1为飞行器投影－目标距离，参照式（4）可得

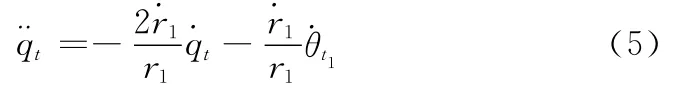
又由于r1＝r cos qd，则

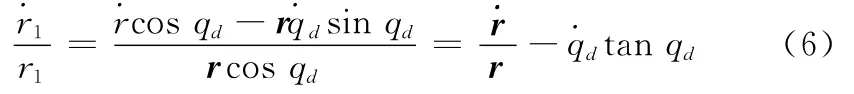
将式（6）代入式（5）得

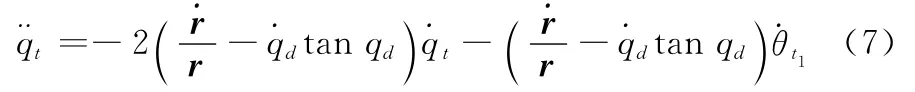
从图1可以看出，单位矢量ed始终保持在水平面x Oz内，其转动角速率与qt变化严格一致，故

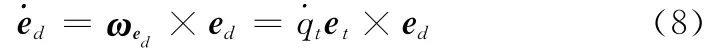
令ecet×ed，则有

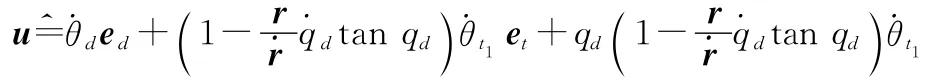
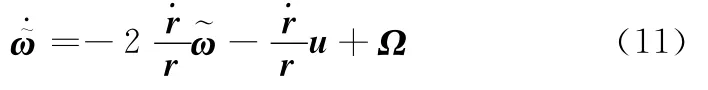
式中，u为制导控制项；Ω为运动耦合项。从其表达式可以看出，在飞行器进行高速大空域机动制导时，Ω将具有较大的值，在制导设计过程中不可简单忽略。

由此，基于视线旋量和旋量速度，可得三维非线性制导的参考旋量模型为

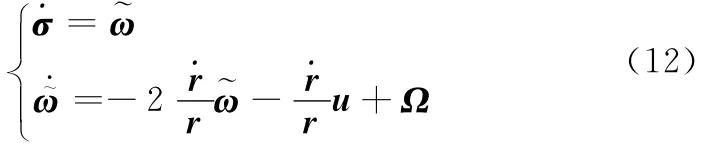
式（12）完整地描述了视线旋量和视线旋量速度之间的变化关系。

2 伪最优滑模制导律设计

三维非线性旋量参考模型较好地体现了运动耦合对飞行器制导的影响，完整地描述了飞行器制导过程的运动规律。但实际上，在高超声速飞行器末制导过程中，其制导控制系统不可避免地会受到各种扰动的影响，因而实际制导模型可以表达为

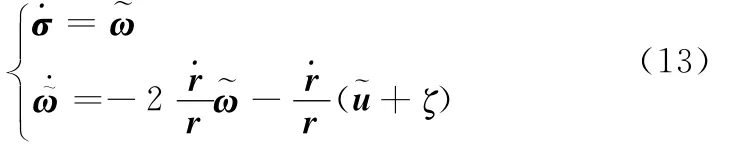
2.1 三维非线性滑模制导律设计

对于同时存在落角和入射方位角约束的问题，制导的目的是使视线转动到一个确定的方向，并保持视线角速度的稳定。根据视线旋量的视线旋量速度的定义，制导目的可以等价描述为

因而令滑模超平面切换函数为

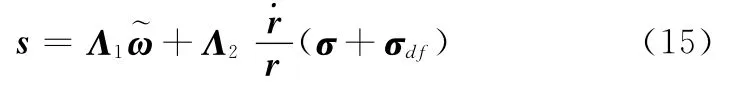
式中，Λ1三维正定常值对角矩阵；Λ2为三维非负常值对角矩阵。Λ1、Λ2分别代表和σ+σdf在滑模切换面中的权重。显然对于无终端角度约束情况，可令Λ2＝03×3。

对式（15）进行求导

为了改善滑动模态的动态品质，由于一般情况下有r＞0，.r＜0，在此采用趋近律的方法构造一种自适应指数趋近律

式中，Λd为三维正定常值对角矩阵；ε为小常值三维向量，该趋近律具有趋近速度快，抖振小的优点。

综合式（13）、式（16）和式（17）可得三维非线性变结构制导律的一般形式

2.2 稳定性证明

稳定性是保证系统正常工作的必要条件。在此依据李雅普诺夫稳定性定理，证明制导系统在所设计制导律作用下的稳定性。

依据滑模动态可达性，构造李雅普诺夫函数

式中，‖·‖1、‖·‖2分别表示向量的1范数和2范数，函数V满足李雅普诺夫稳定性判据。若~ω≠0且σ+σdf≠0，则

可知系统将在有限时间内可达。

2.3 制导参数优化

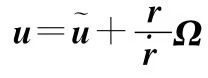
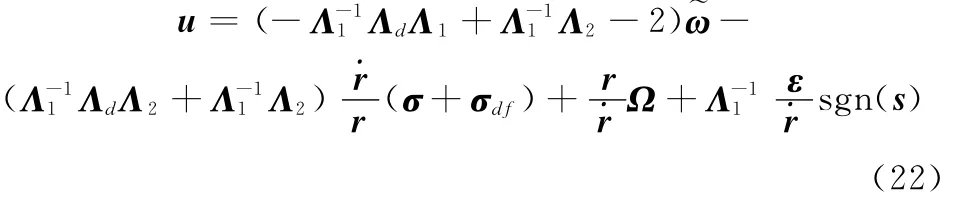
而当不考虑参数扰动情况时，旋量模型式（13）可以转化为

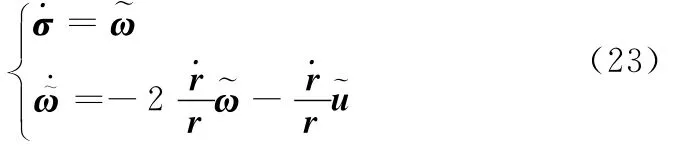
基于极大值原理可得最优伪控制变量。设计相应的二次型目标函数

（1）无终端约束情况

制导律设计中一个常用的等价准则是视线角速率趋于零，可以等价于视线旋量速度趋于零：~ω→0。对于无终端角度约束情况，可得状态方程

式中，P可由逆Riccati方程求解得到

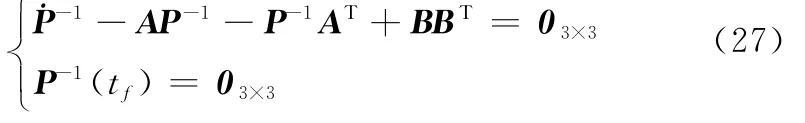
［15-16］，解式（27）得

从而

（2）有终端约束情况

从而得到形如式（25）的状态方程

式中

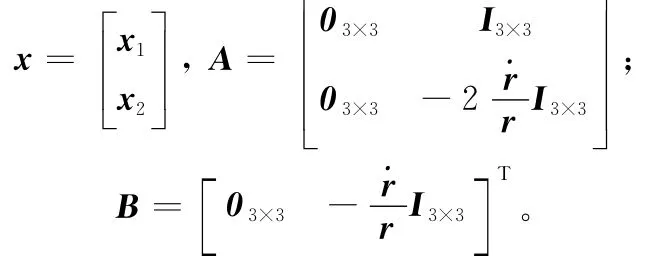
则最优控制为

式中，P可由式（33）的逆Riccati方程求解得到。

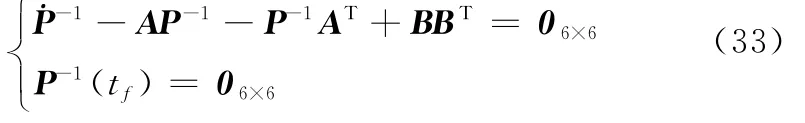
参考文献［15-16］，得

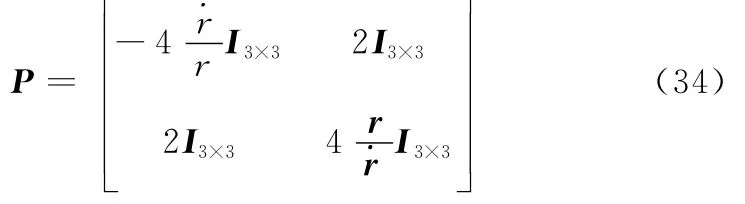
从而

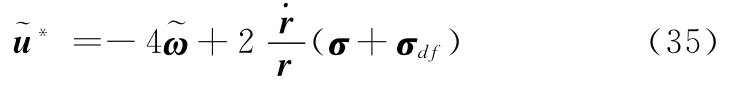
（3）参数设置

由式（29）、式（35）对照式（22）可知，当Λ1＝I3×3，Λd＝I3×3，Λ2＝03×3时，无终端约束条件下的伪最优滑模制导律为

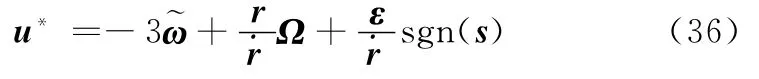
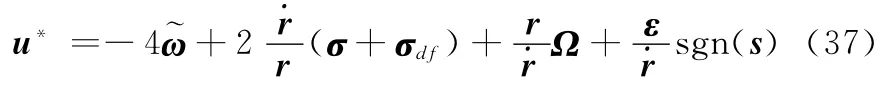
3 实验仿真

本节以某BTT-180型飞行器为对象进行相关验证实验，基本参数设置如表1所示。

表1 仿真基本参数

为了验证制导方法在扰动条件下的鲁棒性，在气动系数、大气密度、视线角度、视线角速率等基本参数上叠加高斯噪声，在此，将目标运动视作未知有界扰动，包含于视线角偏差和视线角速率偏差中，对应的偏差参数设置如表2所示。

表2 干扰偏差设置（3σ）

3.1 仿真算例1 无终端约束攻击目标

初始速度方向设为－30°（以正北为基准，逆时针为正），采用本文方法（式（36））进行仿真实验，经过500次模拟打靶，得到无终端约束情况下的仿真结果如图2和图3所示。从图2和图3可以看出，制导终端东向偏差和北向偏差均较小，脱靶量基本保证在1 m以内，因而在所施干扰条件下，该制导律能够保证高超声速飞行器实现对远程高价值目标的精确打击。

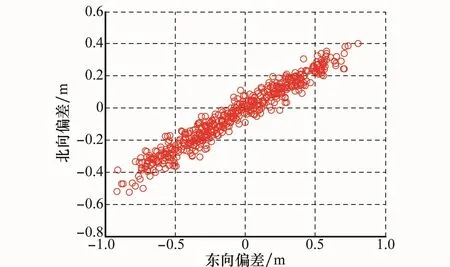
图2 无终端约束下的落点偏差分布

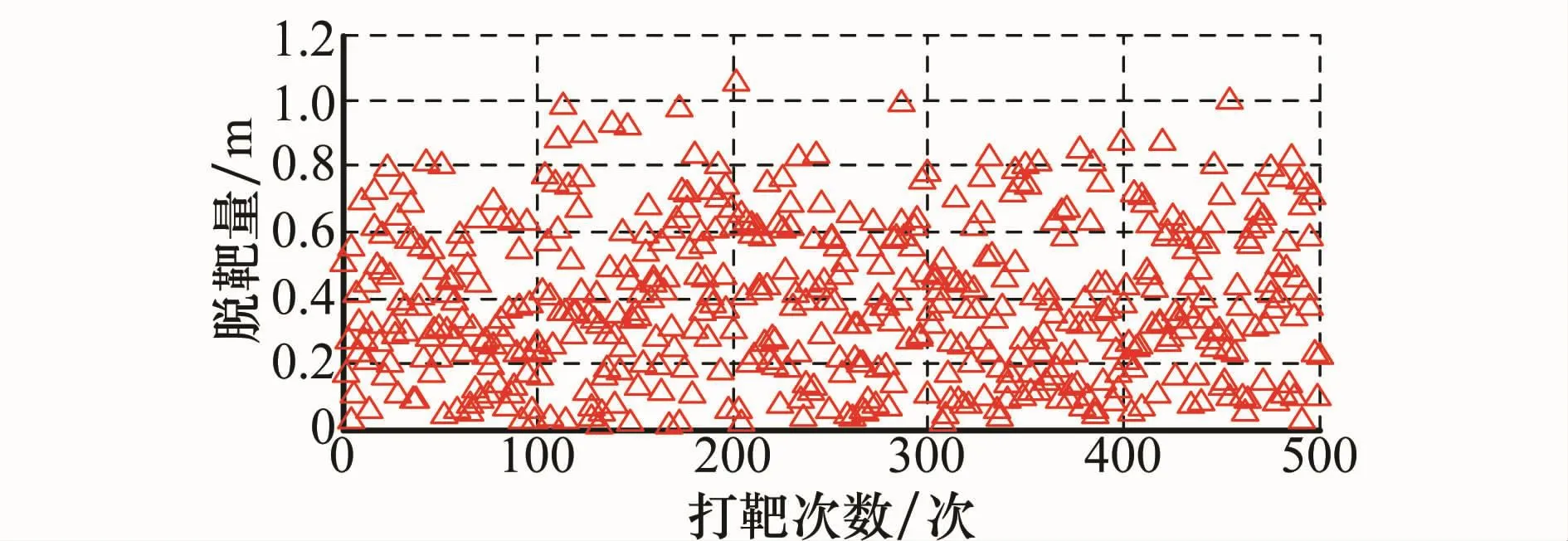
图3 无终端约束下的脱靶量分布

图4～图7为单项偏差在极限情况下的典型弹道仿真结果，从图4可以看出，在整个飞行过程中，飞行弹道光滑，且末段平直，这说明在本文所设计制导律的作用下，高超声速飞行器能够实现对目标的瞄准式攻击。从图5可以看出，升力系数偏差和大气密度偏差对无终端弹道影响较大，其次为实现高低角速率偏差，其他干扰因素对弹道影响较小。从图6（线条区分参照图5，下同）和图7可以看出，攻角、倾侧角在整个飞行过程中变化平稳，在飞行末段，攻角均收敛为较小值，这说明制导过程是鲁棒的。

通过仿真算例1可以看出，在有诸多扰动和噪声的情况下，本文所提出的伪最优滑模制导律依然能够保持较高的制导精度，制导鲁棒性较强，能够满足高超声速飞行器精确制导的需要。

图4 无终端约束下的全程三维弹道曲线

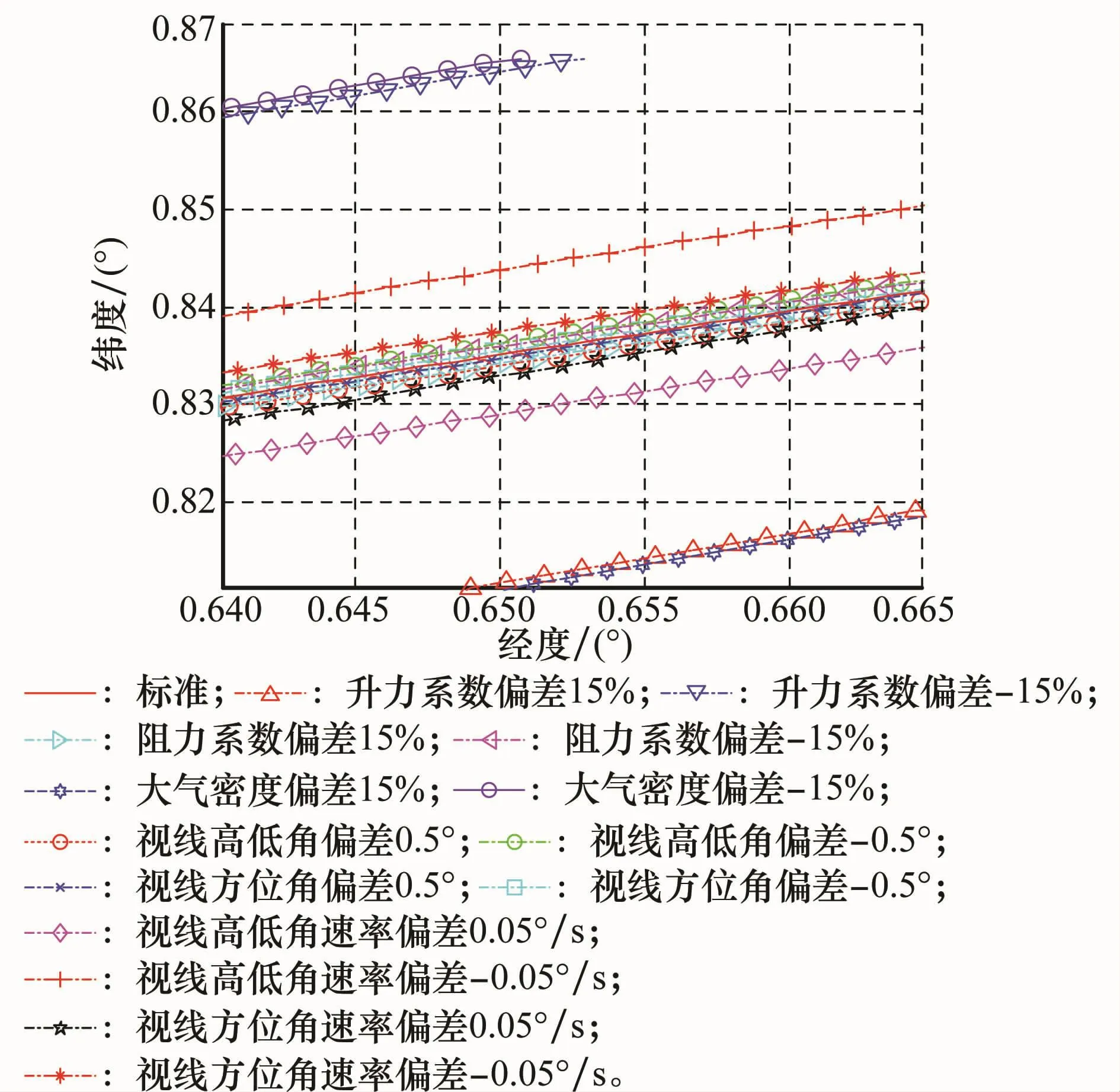
图5 单项偏差干扰下的局部三维弹道曲线

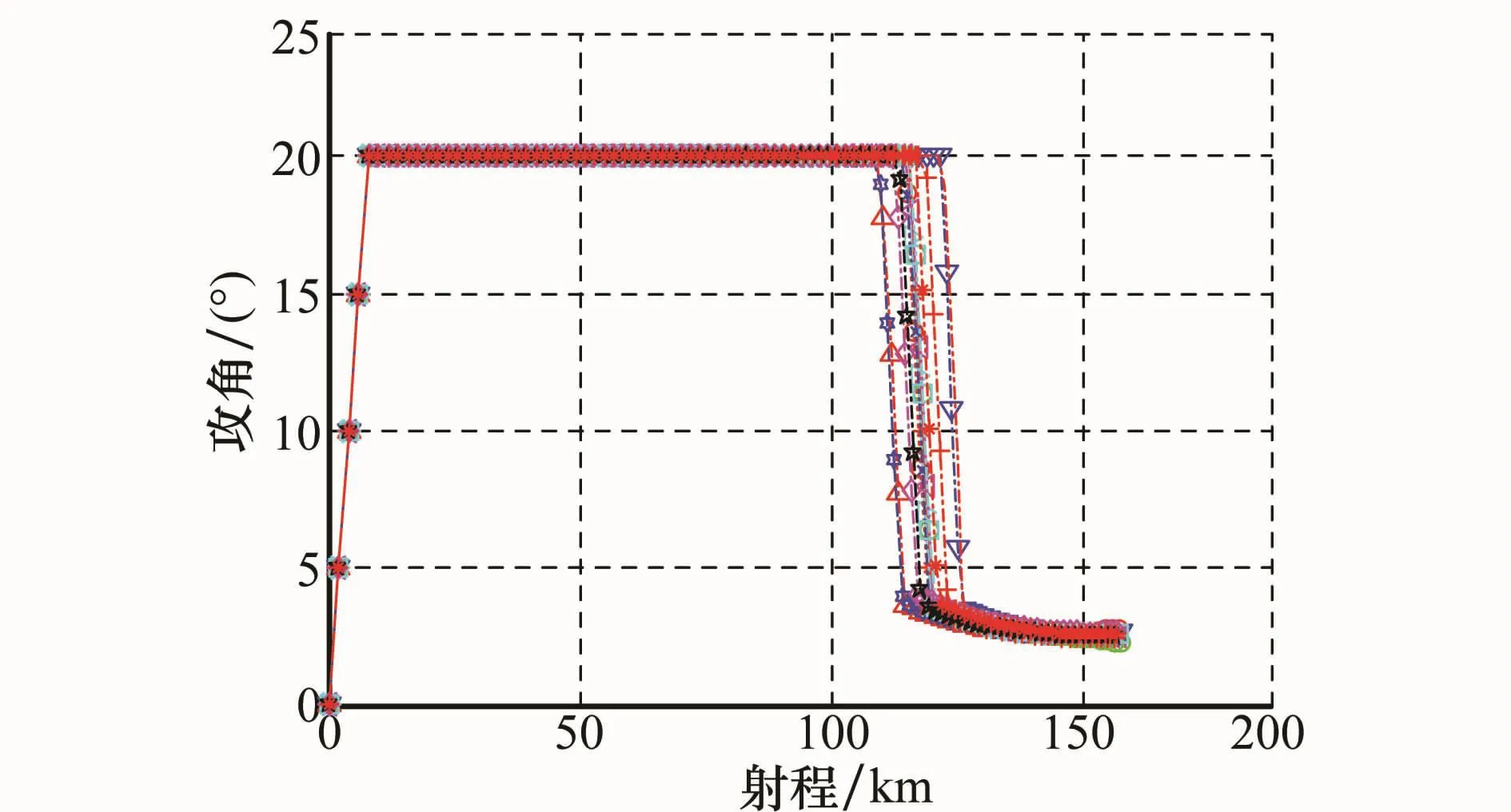
图6 无终端约束下的攻角射程曲线

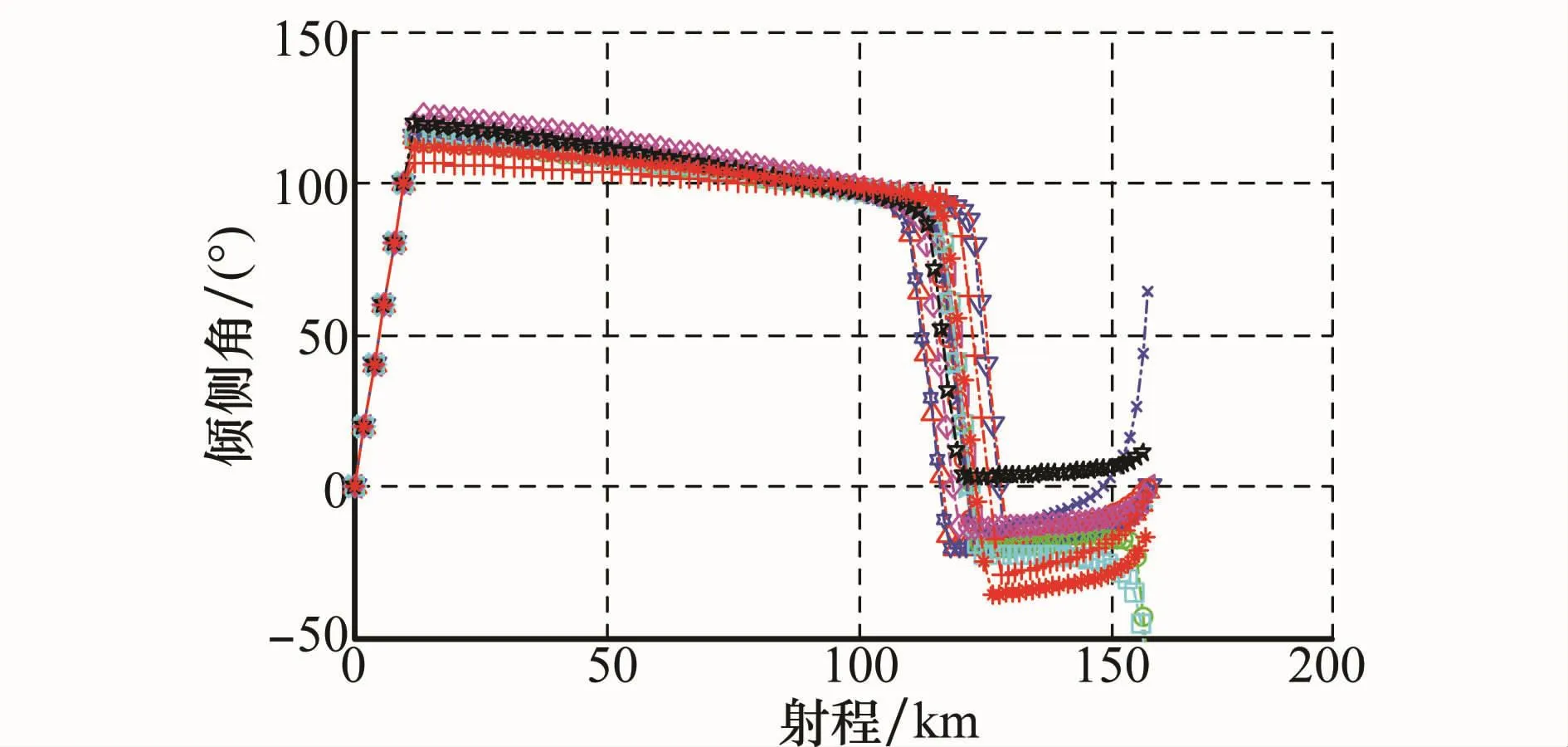
图7 无终端约束下的倾侧角射程曲线

3.2 仿真算例2 有终端约束攻击目标

初始条件同仿真算例1，假设目标位于山谷中，依靠山峰作为天然屏障，为了对目标实施有效攻击，需要避开山峰的障碍，采用式（37）的制导律，可以通过设置合适的入射方位角来降低对弹道落角的要求。设预定入射方位角为－30°，预定落角为－60°。通过500次模拟打靶，得到仿真结果如图8～图11所示。

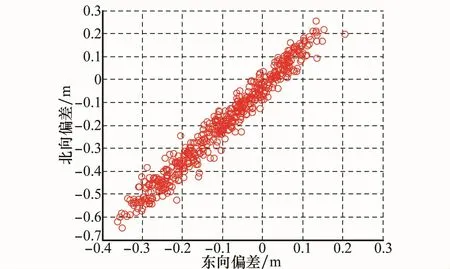
图8 有终端约束下的落点偏差分布

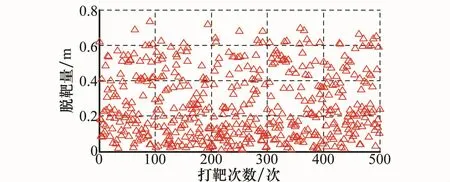
图9 有终端约束下的脱靶量分布

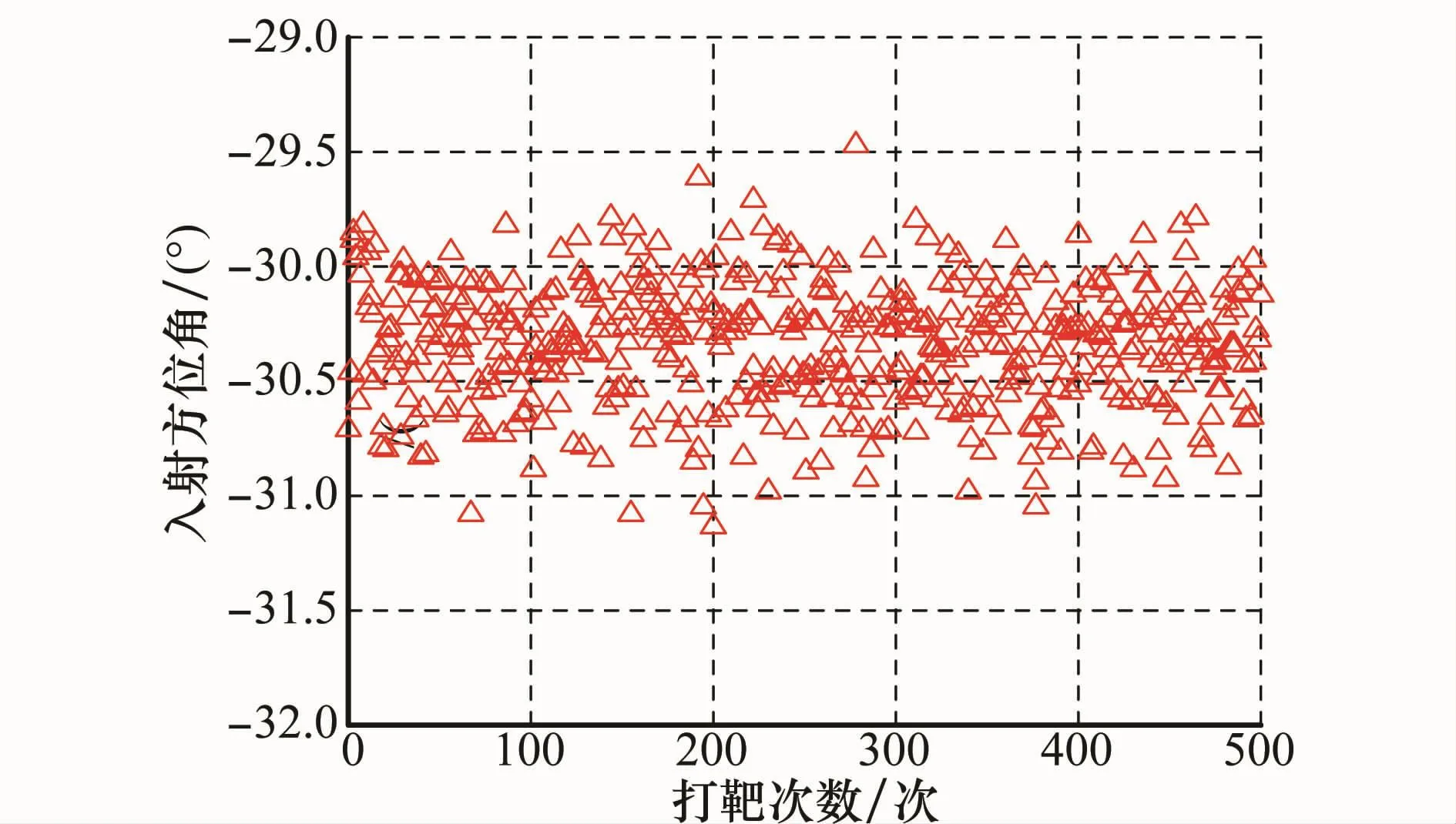
图10 有终端约束下的入射方位角分布

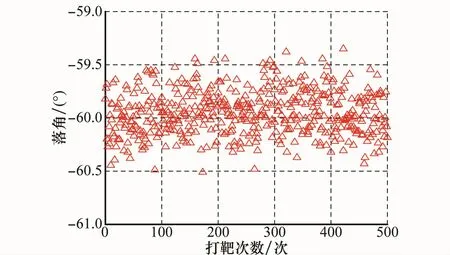
图11 有终端约束下的落角分布

从图8和图9可以看出，在有终端角度约束条件下，制导终端偏差较小，脱靶量小于1 m，满足制导精度要求。从图10和图11可以看出，入射方位角偏差和落角偏差均基本小于0.5°，角度控制精度较高，从而能够保证飞行器避开山峰障碍，使得飞行器从预定入射方位角和落角对目标实施精确打击。

图12～图17为单项偏差在极限情况下的典型弹道仿真结果，从图12可以看出，飞行弹道光滑平稳，飞行器有效地避开了山峰的障碍，能够从山峰之间对山谷目标实施有效的“点穴式”打击，图13所示的局部放大图更好地说明了这一点。从图14和图15可以看出，在终端约束条件下，弹道能够精确地调整到期望的入射方位角和落角，从而满足多约束情况下的精确打击需求。从图16和图17可以看出，攻角、倾侧角指令变化比较平稳，能够保证制导的稳定性。

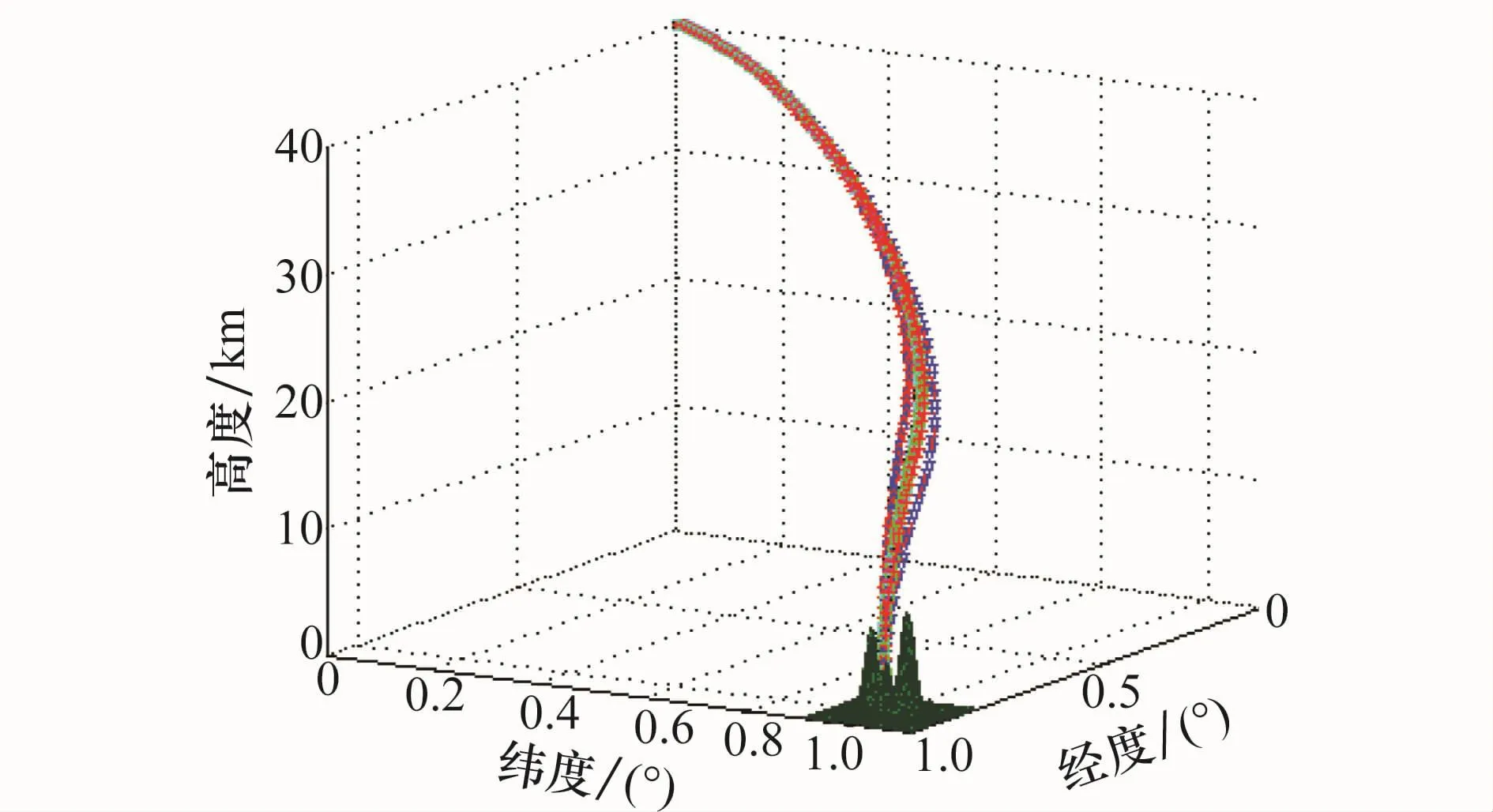
图12 有终端约束下的全程三维弹道曲线

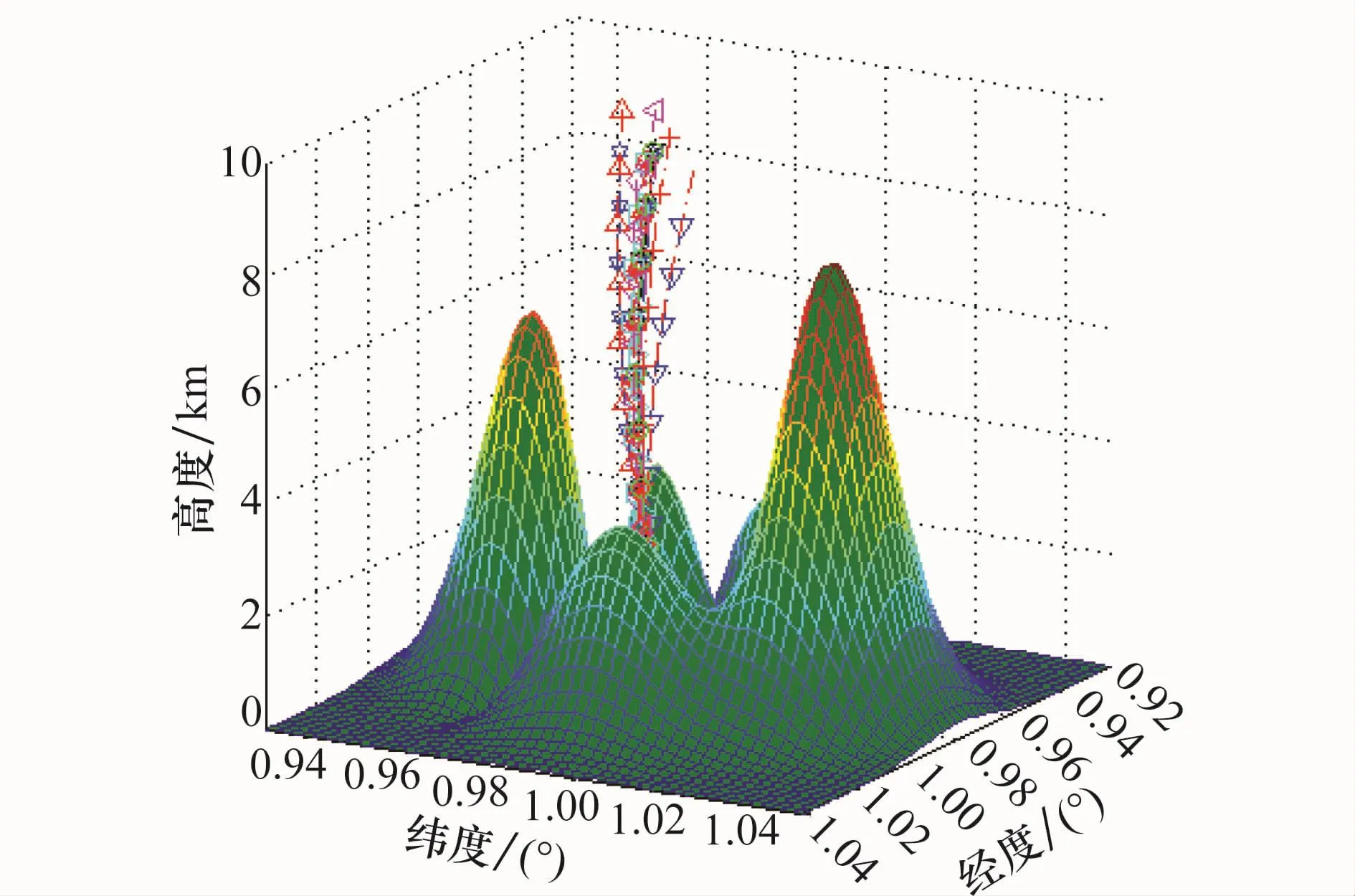
图13 单项偏差干扰下的局部三维弹道曲线

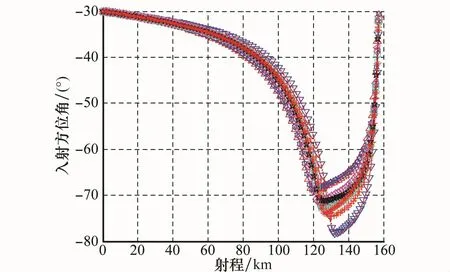
图14 有终端约束下的入射方位角射程曲线

图15 有终端约束下的落角射程曲线

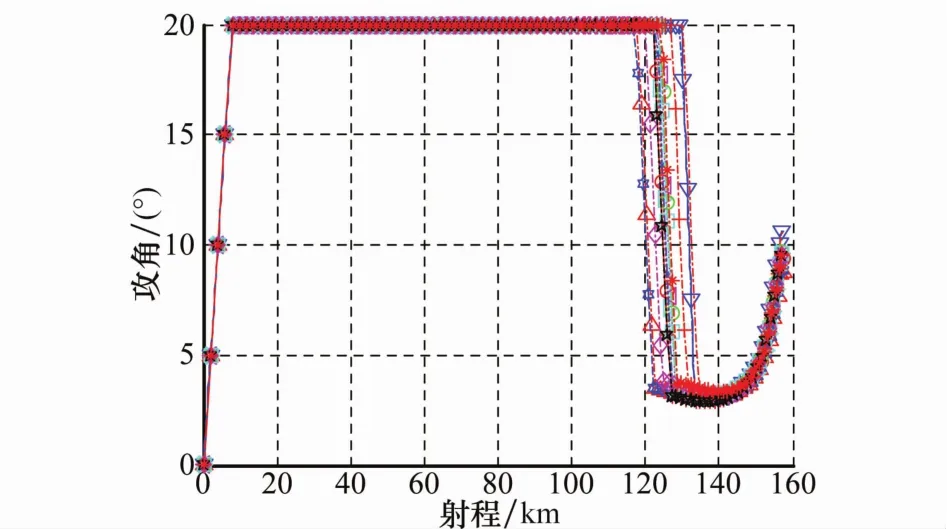
图16 有终端约束下的攻角射程曲线

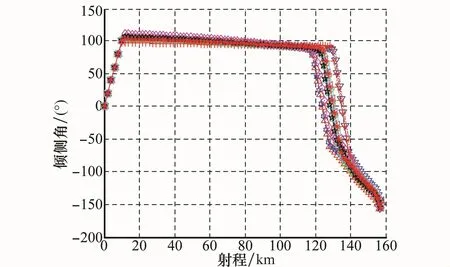
图17 有终端约束下的倾侧角射程曲线

通过仿真算例2可以看出，所提出的伪最优三维滑模制导律通过选择合适的入射方位角，能够降低传统制导律［15］对落角的高要求，满足多约束条件下精确制导的需要。在有诸多扰动因素的情况下，飞行器依然能够保持较高的制导精度，实现多约束条件下的精确制导。

图2和图8中落点偏差均呈“带状”分布，主要原因是本文为了验证制导律的有效性，仿真条件设置相对苛刻，初始射向相对偏离射面较大，飞行器在制导律的作用下，较长时间处于控制至飞行器-目标视线对准并稳定的过程，在快接近目标阶段完成对准，而此时，由于干扰因素的影响，干扰力和干扰力矩叠加在飞行器目标视线方向，因而使得飞行器落点呈“带状”分布。

4 结论

面向高超声速飞行器末制导过程中的运动耦合、参数扰动等突出问题，基于旋量方法完成了三维非线性伪最优滑模制导律的设计。通过仿真算例可知，在诸多干扰因素影响下，本文所研究的滑模制导律能够实现对目标精确攻击，满足终端多种约束要求，且控制变量均未出现明显抖动，鲁棒性较好。本文工作对于研究高超声速飞行器俯冲攻击制导具有较强的参考意义。

参考文献：

［1］She W X，Zhou F Q.Hig h precision 3D nonlinear variable structure guidance law for homing missile［J］.Journal of Astronautics，2004，25（6）：681-685.（佘文学，周凤岐.三维非线性变结构寻的制导律［J］.宇航学报，2004，25（6）：681-685.）

［2］Xiao Y L，Jin C J.The principle of flight in atmospheric disturbance［M］.Beijing：National Defence Industry Press，1993：1-72.（肖业伦，金长江.大气扰动中的飞行原理［M］.北京：国防工业出版社，1993：1-72.）

［3］Sun W M.Research on guidance law design with terminal impact angle constraints in air-to-surface guided weapon［D］.Changsha：National University of Defense Technology，2008.（孙未蒙.空地制导武器多约束条件下的制导律设计［D］.长沙：国防科技大学，2008.）

［4］Brierley S D，Longchamp R.Application of sliding-mode control to air-air interception problem［J］.IEEE Trans.on Aerospace and Electronis Systems，1990，26（2）：306-325.

［5］Zhou D，Mu C D，Xu W L.Adaptive sliding-mode guidance of a homing missile［J］.Journal of Guidance，Control，and Dynamics，1999，22（4）：589-594.

［6］Zhou D，Zou X G，Sun D B.A sliding-mode guidance law for homing-missiles breaking through defense with maneuver［J］.Journal of Astronautics，2006，27（2）：213-216.（周荻，邹昕光，孙德波.导弹机动突防滑模制导律［J］.宇航学报，2006，27（2）：213-216.）

［7］Zhou D，Hu H Z，Hu G H.An adaptive variable structure guidance law［J］.Journal of Astronautics，1996，17（4）：9-12.（周荻，胡恒章，胡国辉.一种自适应变结构制导律［J］.宇航学报，1996，17（4）：9-12.）

［8］Zhou D，Mu C D，Ling Q，et al.Study of optimal sliding-mode guidance law［J］.Chinese Juournal of Aeronautics，1999，12（4）：236-241.

［9］Sun W M，Zheng Z Q.3D variable structure guidance law on adaptive model-following control with impact angular constraints［C］∥Proc.of the 26th Chinese Control Conference，2007：61-64.

［10］Guo J G，Zhou F Q，Zhou J.Variable structure terminal guidance law based on zero miss-distance［J］.Journal of Astronautics，2005，26（2）：152-155.（郭建国，周凤岐，周军.基于零脱靶量设计的变结构末制导律［J］.宇航学报，2005，26（2）：152-155.）

［11］Kim B S，Lee J G.Homing guidance with terminal angular constraint against nonmaneuvering and maneuvering target［R］.American Institute of Aeronautics and Astronautics，Inc，AIAA-97-3474，1997.

［12］Lin C M，Hsu C F.Guidance law design by adaptive fuzzy sli-ding-mode control［J］.Journal of Guidance，Control，and Dynamics，2002.25（2）：248-256.

［13］Bahrami M，Ebrahimi B，Roshanian J.Optimal sliding-mode guidance law for fixed-interval propulsive maneuvers［C］∥Proc.of the IEEE International Conference on Control Applications，2006：1014-1018.

［14］Li D，Wang Q C.Robust sliding mode control guidance law for interceptor based on wavelet neural networks［C］∥Proc.of the 6th World Congress on Intelligent Control and Automation，2006：2199-2203.

［15］Chen K J，Zhao H Y.An optimal guidance law of maneuvering reentry vehicle attacking ground fixed targets［J］.Journal of Astronautics，1994，15（1）：1-7.（陈克俊，赵汉元.一种适用于攻击地面固定目标的最优再入机动制导律［J］.宇航学报，1994，15（1）：1-7.）

［16］Xu M L，Liu L H，Tang G J，et al.Design of dive trajectory of hypersonic near-space vehicle with minimum hinge moment［J］.Journal of Ballistics，2011，23（3）：1-6.（徐明亮，刘鲁华，汤国建，等.高超声速临近空间飞行器铰链力矩最小俯冲弹道设计［J］.弹道学报，2011，23（3）：1-6.）

Three-dimensional nonlinear sliding mode guidance law for hypersonic vehicle

PENG Shuang-chun，ZHU Jian-wen，TANG Guo-jian，CHEN Ke-jun
（College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China）

A novel three-dimensional（3D）nonlinear pseudo optimal sliding mode guidance law for hypersonic vehicle is proposed to resolve the motion coupling and parameter perturbation problems.Firstly，aiming at the motion coupling problem，a 3D nonlinear reference guidance model of hypersonic vehicle is constructed based on line-of-sight（LOS）twist and its rate after their concepts is defined.Secondly，in order to depress the influence of parameter perturbation，a 3D nonlinear sliding mode guidance law adapted to multi-constraint guidance is deduced based on variable structure control theory.Moreover，the stability of this guidance law is proved through theory deduction.Finally，a novel 3D nonlinear pseudo optimal sliding mode guidance law is designed，after its parameters are optimized by introducing pseudo control variable.With the novel guidance law，the motion coupling and parameter perturbation problems can be well avoided and optimal characteristic of guidance parameters is ensured as well.The validity of the guidance law is also validated through simulation experiments.

hypersonic vehicle；pseudo optimal sliding mode guidance law；twist technology；motion coupling；parameter perturbation

V 448 文献标志码：A DOI：10.3969／j.issn.1001-506X.2015.09.19

彭双春（1979-），男，博士，主要研究方向为精确制导、弹道设计。

E-mail：pengshuangchun＠sohu.com

朱建文（1987-），男，博士研究生，主要研究方向为精确制导。

E-mail：zhujianwen1117＠163.com

汤国建（1964-），男，教授，博士研究生导师，主要研究方向为飞行器动力学、制导与控制技术。

E-mail：tangguojian＠nudt.edu.cn

陈克俊（1956-），男，教授，主要研究方向为飞行器动力学、制导与控制技术。

E-mail：chenkejun＿nudt＠sohu.com

1001-506X（2015）09-2080-08

2014-10-24；