基于Nastran的球轴承接触问题有限元分析

段磊，陈晓阳，张涛

(上海大学 机电工程与自动化学院，上海 200072)

滚动轴承是机械传动中重要的零部件[1]，轴承接触应力影响着轴承的接触疲劳和磨损，决定着轴承的可靠性寿命。

滚动轴承内、外圈和滚动体之间的接触面为椭圆。目前Hertz理论法相对成熟[2]，但要求作用力与接触面垂直是其局限性，不能计算考虑摩擦问题的轴承接触问题。不少学者利用有限元软件对轴承进行接触分析[3-6]，当2个物体接触时，其最大接触应力、接触变形不同，且最大接触应力也不在接触点上，不符合Hertz接触理论。针对这一问题，文中首先利用Patran & Nastran软件,建立球-板有限元接触模型,探讨有限元网格的划分方法以及最大接触应力和接触区域形状不等的原因，然后以某型深沟球轴承为例，说明此有限元网格划分方法的可行性。

1 球-板模型有限元分析

1.1 建模和网格划分

对62306-2RS轴承进行建模分析，球半径为5 mm，板长宽高均为0.5 mm，作用力为200 N，材料均为GCr15，弹性模量为207 GPa，泊松比为0.3。由于球与板接触具有对称性，故只对1/4球-板模型进行分析，其模型如图1所示。

图1 球-板接触模型

为兼顾计算精度和速度，采用六面体划分网格，非接触区域网格划分较粗，接触区域网格划分较细。采用Patran软件对球体划分六面体网格的要求较严格[7]，如果直接在一个面上划分面网格，然后扫掠为体网格，则扫掠轴线位置为五面体网格；用自动生成网格功能划分则有四、六面体存在。因此，对1/4球体不能直接划为完全六面体网格。首先将球分割为2部分，中间部分用meshing中sweep>loft划分，另一部分可先在面上划分六边形网格，再旋转得到六面体网格。板为规则形状，可直接划分六面体网格。此外，采用布种子节点的方法来控制接触区域网格尺寸，如图2所示。通过调整网格数量，获得30组网格疏密不同的接触有限元模型，将求解结果与Hertz理论结果对比发现，当球的单个网格尺寸等于a/3.9时(a为椭圆接触区域的长半轴)，接触形状、最大接触应力和弹性趋近量最接近Hertz理论解。

图2 球-板接触模型网格划分

1.2 约束与载荷

将垂直于z轴的圆平面设为刚性面，然后在该平面上沿z轴施加50 N的载荷(1/4模型)。分别约束模型在x，y方向的位移以及板底面的位移。

1.3 接触和边界条件

球和板均设置为变形体；接触问题为边界非线性问题，未考虑摩擦因素，不设置摩擦类型和摩擦参数；接触区域应变很小，非线性几何影响因素设置为小位移小应变类型；设置输出节点和单元的力、位移、应力、法向接触力、法向接触应力。

1.4 结果分析

接触区域球的单个网格尺寸为a/3.9时，球-板模型接触区域应力云图如图3、图4所示。

图3 球应力云图

图4 板应力云图

由图可知，球的最大接触应力为 2 650 MPa，不在初始接触点(图2中黑点处)。板的最大接触应力为2 840 MPa，在初始接触点上。这与Hertz理论分析结果不同。其原因如下：有限元法是先把物体分为有限个单元体，计算出总体刚度矩阵K和所有节点的等效节点力矩阵F，然后根据F=Kδ得出所有节点的位移矩阵δ，最后利用应力矩阵σ=Sδε(S为常数矩阵，δε表示某个单元的节点位移矩阵，指数ε与单元有关)算出单元的应力矩阵σ，但计算结果要求得出单元节点的应力。根据有限元近似解性质[8]，应力和应变近似解一定是在精确解上下浮动，单元的应力在高斯积分点上，然后利用单元形函数将高斯节点的应力插值到单元节点上。这样相邻单元仅在相邻的节点与边界上变形连续，而非相邻的边界上并不一定相等，导致两相邻单元在相邻节点上计算的应力不连续，一般采用绕节点平均或应力磨平等方法进行处理。

通过Patran后处理提取球和板在接触面上接触区域的接触点编号及应力如图5、图6所示。图中，括号内为节点的法向接触应力，括号上面为对应的节点编号。

图5 球在接触区域的网格

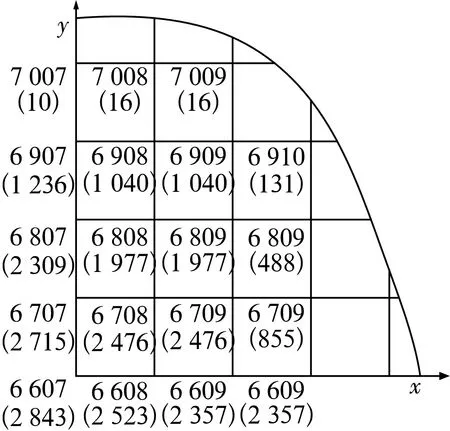
图6 板在接触区域的网格

由图可知，球和板的最大接触应力分别为2 645 MPa和2 843 MPa，分别在节点233和6 607上。通过有限元理论可知，节点233和6 607上的接触应力均是由对应网格上高斯节点的应力等效得到。单元上高斯点应力插值和绕节点平均或应力磨平等方法导致其最大接触应力不在初始接触点232上。因此造成球和板上最大接触应力数值不等和位置(初始接触点)不同。

球和板法向接触应力随边界变化如图7、图8所示。由图可知，球和板接触区域长半轴a分别为0.193 2 mm和0.211 4 mm。通过Patran后处理提取球和板接触面上接触应力可得，球和板所有节点的接触应力之和均为49.9 N，约等于施加的外力50 N，可以说明在接触面上球和板的等效节点力F基本相同，又由于球和板在接触区域的网格不同，则其刚度矩阵K不同，由F=Kδ可知，接触区域半径会有微小差别，因此造成球和板接触区域长半轴不等。

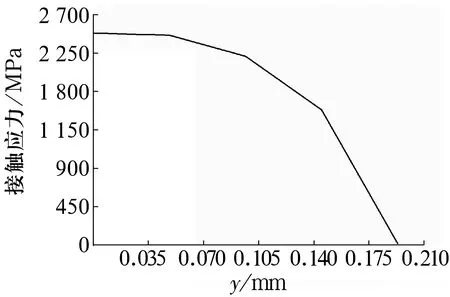
图7 球法向接触应力随接触边界变化图

图8 板法向接触应力随接触边界变化图

接触区域球的单个网格尺寸为a/3.9时，球-板模型接触区域位移云图如图9、图10所示。

图9 球位移云图

图10 板位移云图

由图可知，板的绝对最大位移为2.93 μm，在初始接触点6 007上，球的绝对最大位移为6.54 μm，在球心点上。则板的中心(无穷远处)相对于初始接触点的位移为2.93 μm，球的中心相对于初始接触点的变形量为3.61 μm。由Hertz接触理论可知，2个接触物体的弹性趋近量为初始接触点处各自所对应的圆弧中心在接触过程中所移动的距离之和，球-板接触模型的弹性趋近量为6.54 μm。

由于单元网格大小和形函数不同，最大接触应力值不同。球-板模型最大接触应力及接触半径取球和板的平均值，其与Hertz理论结果对比见表1。

表1 球-板有限元解与解析解

由表1可知，有限元解与 Hertz 理论解误差在工程允许的范围内，故利用有限元软件来解决接触问题是可行的。

2 实例计算

2.1 建模

以某型深沟球轴承模型为例，其参数为：外径D=9 mm，内径d=4 mm，宽度B=2.5 mm，球数n=8，球径Dw=1.3 mm，内外圈和球的材料为GCr15，弹性模量为207 GPa，泊松比为0.3，额定静载荷189 N，仿真中径向载荷取40 N。

由于轴承具有对称性，且仅有3个球受力，为减少网格数量，对其3/8模型进行有限元分析。利用上述方法进行网格划分得出其模型如图11所示。

图11 3/8轴承有限元模型

2.2 设置边界条件

为模拟轴对内圈的作用力，将内圈内表面设置为刚性，然后在轴承中心点上沿x轴(图11)方向施加40 N载荷。

外圈外表面所有节点约束x方向位移；内外圈端面所有节点约束z方向的位移；在柱坐标系下约束球与内外圈接触点连线上所有节点的周向和轴向自由度；约束球在xOy平面上所有节点，z方向的位移，如图 12所示。

图12 轴承有限元模型

2.3 结果分析

通过Nastran软件仿真计算后得到球与内圈接触的应力和位移云图如图13～图16所示。

图13 内圈上接触应力云图

图14 内圈上接触位移云图

图15 球上接触应力云图

图16 球上接触位移云图

由图可知，球与内圈的接触区域为椭圆，接触应力和变形由接触中心向外逐渐减小，符合实际情况。球与外圈接触情况与此相同。

轴承中受力最大球的最大接触应力及变形有限元解与解析解的对比见表 2。有限元解与解析解误差在工程允许范围内，故利用有限元软件来解决轴承接触问题能满足工程实际应用，而且可以图形的形式直观地显示接触应力、接触尺寸、弹性趋近量等。

表2 受力最大球有限元解与解析解比较

轴承中受力最大球相邻2个球的最大接触应力、变形有限元解与轴承解析解见表 3。

表3 受力最大球相邻球有限元解与解析解

通过对轴承中与受力最大球相邻的2个球的有限元解和解析解对比可知，其误差较大。这是由于接触区域网格是以最大球与内圈接触为基准划分的，相对相邻球接触区域网格划分更粗，误差相对较大。

3 结束语

通过有限元法与轴承解析法对比可知，利用有限元软件来解决轴承接触问题是可行的。

1)采用有限元软件对多组不同网格尺寸的球-板接触模型分析可知，当球的单个网格尺寸等于a/3.9时，得到最佳结果。

2)在有限元软件分析中，2个接触物体同一接触点最大接触应力不同和最大接触应力不在初始接触点是由于网格差异和软件插分算法引起的。

3)网格划分对接触区域、接触应力影响很大，为保证最大接触应力准确，对于轴承划分网格，应以受力最大球的接触区域为基准。

由于球-板模型和轴承模型弹性趋近量误差相对较大，需进一步分析原因。