基于HVD与1.5维Teager能量谱的滚动轴承故障诊断方法研究
2015-07-26孙熠李志农朱明
孙熠,李志农,朱明
(南昌航空大学 无损检测技术教育部重点实验室,南昌 330063)
滚动轴承是机械设备中应用最广泛的零件,也是最容易发生故障的零件[1]。如内、外圈表面的点蚀等常见的轴承缺陷都会激发出周期性冲击振动[2]。实际工程应用中存在着较多的噪声,故障的冲击特征并不明显,如何有效地提取故障特征频率一直是研究难点。
经验模态分解(EMD)及其扩展算法与Teager能量算子或1.5维能量谱相结合,均能有效提取故障特征频率[3-5]。然而,EMD缺乏严格的理论基础,存在模态混叠的缺陷[6],EEMD则存在计算量巨大,不适合进行在线分析的不足。Hilbert振动分解(Hilbert Vibration Decomposition,HVD)是一种自适应的信号分解方法[7],与EMD相比既保留了分解自适应性,又避免了样条拟合,运算效率及分辨率更高[8-9],在信号解析中能够取得更好的效果[10-14]。因此,将HVD与1.5维Teager能量谱相结合,应用于强背景噪声下的轴承微弱故障信号的特征频率提取中,并通过试验验证该方法的有效性。
1 Hilbert振动分解原理
HVD的实质是将一个复杂的信号分解为一系列幅值不同的分量和1个残余分量之和,为了更方便简单地讨论HVD,选择两分量信号进行说明,其具体的实现步骤如下:
1)对于信号x(t),首先求其Hilbert变换,得其解析信号z(t)。
(1)
(2)
式中:f1(t)为瞬时频率;f2(t)为快速变化不对称频率;a1(t)和a2(t)为瞬时幅值;θ1和θ2为初始相位;i为虚部单位。
则解析信号z(t)的瞬时幅值a(t)和瞬时频率f(t)为
(3)

(4)
当a1(t)>a2(t)时,(4)式中第2项在区间[0,T=1/(f2-f1)]上的定积分为0[7]。因此,可使用低通滤波器去除不对称振荡部分,估计出幅值最大分量的瞬时频率f1(t)[8]。
2)通过同步检波和低通滤波提取出当前幅值最大分量的瞬时幅值ar(t)和相位θr。以估计出的瞬时频率作为参考频率fr(t),将初始信号分别与2个参考正交信号相乘,同相输出z1(t)和正交相输出z2(t)为
(5)
(6)
通过低通滤波器滤除(5),(6)式的第2项,可得
(7)
则瞬时幅值ar(t)和相位θr为
(8)
(9)
3)从原始信号中减去当前检测出的幅值最大分量x1(t),得
xr(t)=x(t)-x1(t)。
(10)
将xr(t)作为新的待检信号替代原始信号,重复前2步,依次获得不同幅值分量,直到迭代结果满足迭代停止条件。
2 1.5维Teager能量谱
Teager能量算子是一种非线性差分算子,能够增强信号的瞬态特征,适合检测信号中的冲击成分。该方法的时间分辨率高,对信号的瞬时变化具有良好自适应能力,而且计算复杂性低,算法效率高。
对于任意连续实信号x(t),Teager能量算子定义为
(11)
应用差分代替微分的方法,可以将连续时间信号的Teager能量算子表示为离散形式
φ[x(n)]=[x(n)]2-x(n-1)x(n+1)。
(12)
1.5维谱定义为随机信号x(t)的三阶累积量c3x(τ1,τ2)的对角切片c3x(τ,τ)(其中τ1=τ2=τ)的Fourier变换。由于三阶累积量对噪声不敏感,因而,由三阶累积量得到的1.5维谱具有优良的噪声抑制能力,是非平稳、非线性、非高斯信号强有力的分析工具。
1.5维Teager能量谱定义为先对信号x(t)做Teager能量算子,然后进行1.5维谱运算。其结合了Teager能量算子能有效地提取冲击特征的特点和1.5维谱良好的噪声抑制能力的优点,特别适合轴承故障信号的特征提取。
在利用HVD 和1.5维Teager能量算子诊断轴承故障时,将HVD得到的各个分量进行相关分析,即将每个分量分别与原始信号进行互相关运算,求解相关系数,取前3个相关系数最大的分量的和信号作为重构信号,重构后的信号能有效地去除轴承的噪声和无关项,增强故障信号的冲击特征,然后,对重构后的信号求1.5维Teager能量谱。
3 试验研究
试验装置见文献[14],试验轴承为6205-2RS JEM SKF深沟球轴承,钢球数为9,钢球直径为7.94 mm,球组节圆直径为39.04 mm。在轴承内圈上应用电火花技术加工凹坑,模拟单点缺陷,故障直径为0.177 8 mm。在驱动端的轴承座上设置加速度传感器测试振动信号,电动机转速为1 790 r/min,相应的转轴频率为fr=29.3 Hz,采样频率fs=12 kHz。计算得轴承内圈故障特征频率为fi=158.2 Hz。
选取2 048个采样点进行分析,内圈故障信号的时域波形如图1所示。从图中可以看出,冲击特征受噪声的干扰比较严重。

图1 内圈故障振动信号的时域图
内圈故障信号的EMD和HVD结果如图2所示。从图中可以看出,EMD前2个分量的波形特征与原信号非常相似,由于EMD在强噪声条件下存在严重的模态混叠现象,原信号没有得到很好的分解;而HVD则将原故障信号有效地分解为若干个调幅调频信号,且局部的冲击特征比较明显。
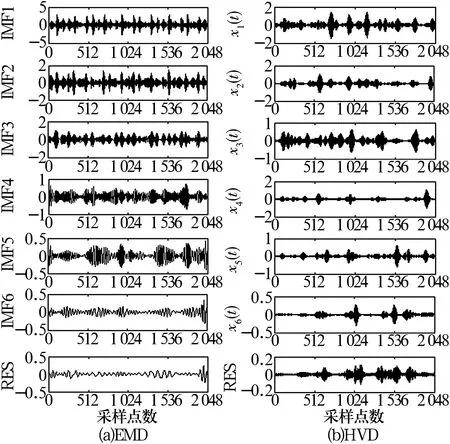
图2 内圈故障振动信号的处理
将上述分解信号进行重构,结果如图3所示。从图中可以看出,EMD重构信号的冲击特征明显不如HVD重构信号,噪声干扰大。
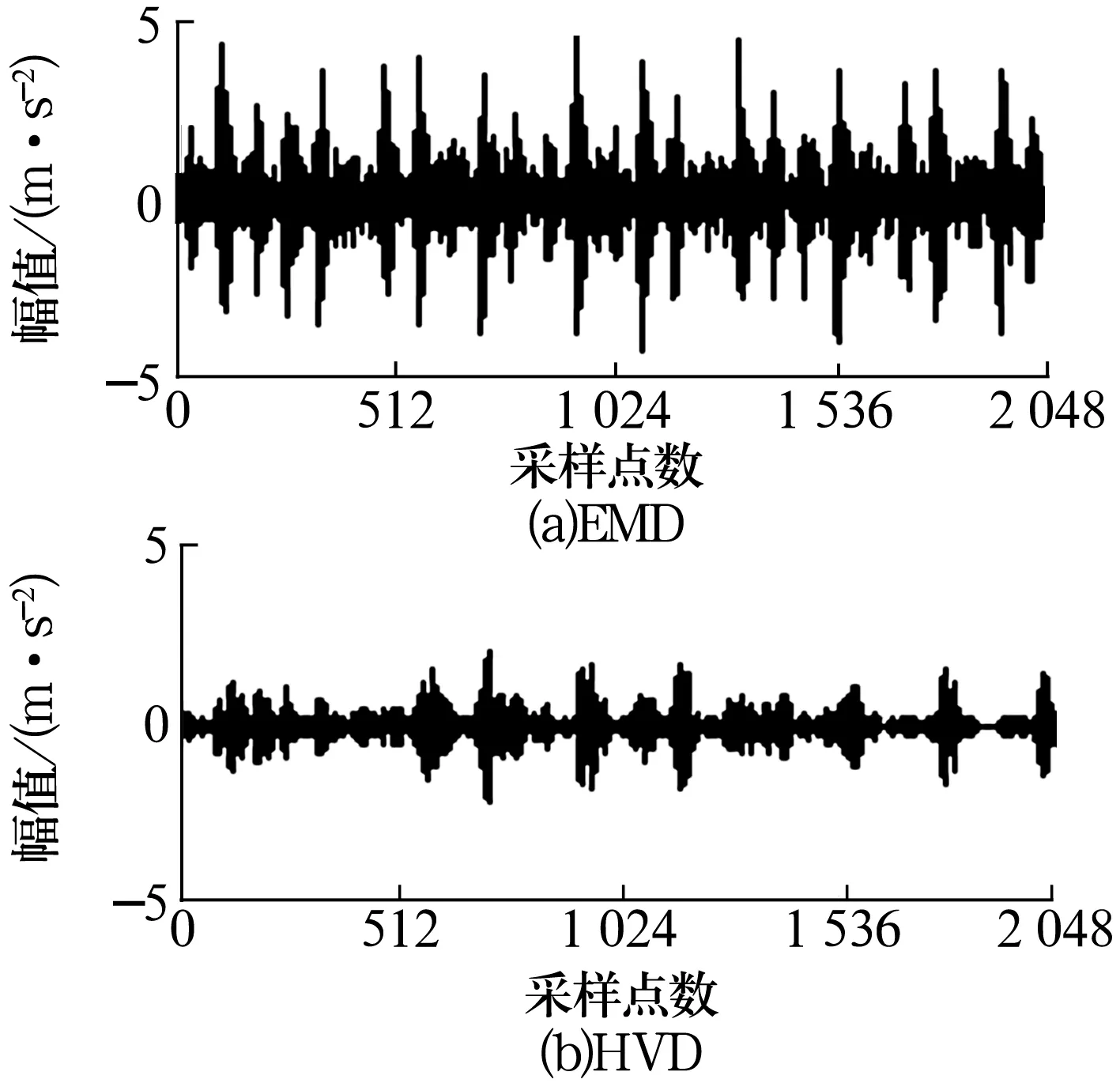
图3 内圈故障信号的重构
重构信号的1.5维Teager能量谱如图4所示。从图中可以看出,EMD在内圈故障特征频率158.2 Hz处存在明显的峰值,不能有效地体现转轴频率的调制频率;HVD在内圈故障特征频率158.2 Hz、轴承基频的二倍频(58.6 Hz)、频率fi-2fr(99.6 Hz)处均存在明显的峰值,其他频率的峰值则显得非常小。
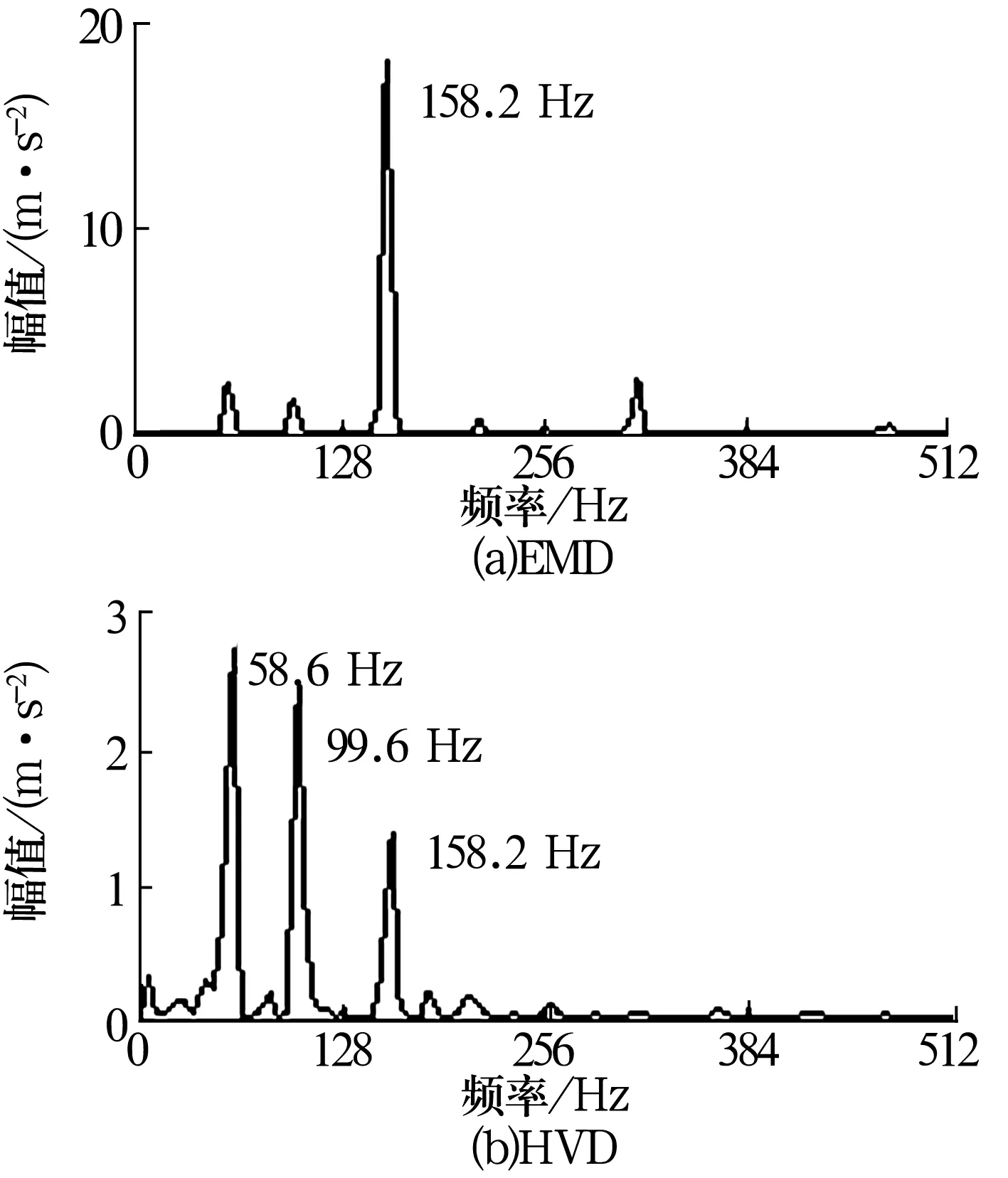
图4 内圈故障重构信号的1.5维Teager能量谱
4 结束语
针对强背景噪声下滚动轴承微弱故障信号特征难以提取的特点,首先通过HVD将故障振动信号分解成一系列调幅调频分量;然后采用相关系数法重构原始信号,增强轴承故障信号的冲击特征;最后分析重构信号的1.5维Teager能量谱,提取故障特征频率。试验结果表明:与EMD相比,HVD在增强冲击特征上有明显的优势,且不存在模态混叠现象,能有效地提取故障特征频率,分析出转轴转频的调制频率,且噪声非常小,效果非常明显。然而,该方法也存在HVD滤波参数的选择,如何更好地重构原始信号等问题,这些将是进一步研究的方向。
