基于SDCS－SVM的大坝安全监测模型

屠立峰 包腾飞 唐 琪 赵 斌

（1.河海大学 水利水电学院，南京 210098；2.河海大学 水资源高效利用与工程安全国家工程研究中心，南京 210098；3.南京南瑞集团公司 国际公司，南京 210003）

建立大坝原型观测模型一直是大坝安全监测的研究重点［1］.在使用过程中，常用的监测模型有逐步回归模型、神经网络模型、支持向量机（SVM）模型等［2］.逐步回归模型的缺陷为只适用于数据样本充分的情况，BP神经网络模型易出现过拟合和收敛过慢的不利现象，以至于限制了以上模型的适用范围和拟合预测精度.SVM模型是一种建立在统计学分析原理上的新型小样本机器学习方法［3］.研究表明，该模型对高维数、小样本问题的解决效果良好，且泛化能力优异.SVM模型预测精度的影响因素主要有惩罚因子c和核函数参数σ，所以惩罚因子和核函数参数的选择对支持向量机模型的建立至关重要.近年来，学者们已经提出了基于遗传算法、粒子群算法、蚁群算法等对SVM的参数进行寻优的优化算法.布谷鸟搜索算法（Cuckoo Search，CS）是一种新型的仿生学算法，该算法依据布谷鸟特殊的存窝产子方式而概括出的，现已在计算机智能系统、多资源均衡优化等方面运用广泛.该算法虽具有控制参数少、全局寻优能力强等优点，但是在计算后期易出现搜索速度过慢的现象［4］.本文遵循最速下降法的迭代修正原则而提出基于最速下降法的混合布谷鸟搜索算法（SDCS），该算法具有简单、高效、在概率选择和适应度的确定上具有自适应性和鲁棒性等优点.实测数据验证表明，通过SDCS算法对SVM模型的惩罚因子c和核函数参数σ进行全局寻优，SDCS－SVM模型较SVM模型和多元回归模型具有更高的精度和泛化能力.

1 支持向量机

支持向量机模型对解决分类和复杂的非线性回归问题卓有成效.SVM的主要思路为将某一输入空间的非线性变量参照内积函数映射到一个高维的空间，并在该高维空间进行线性回归［5］.n维向量样本可表示为：（x1，y1），（x2，y2），…，（xi，yi）∈（Rn×R），通过最优决策函数f（x）＝［ω，φ（x）］＋b将非线性映射φ（x）转化为更高维空间的线性函数.根据结构风险最小化原则寻找ω，b，最小二乘支持向量机在优化目标中的损失函数ε为误差ξi的二次项，优化过程与公式（1）等价［6］：

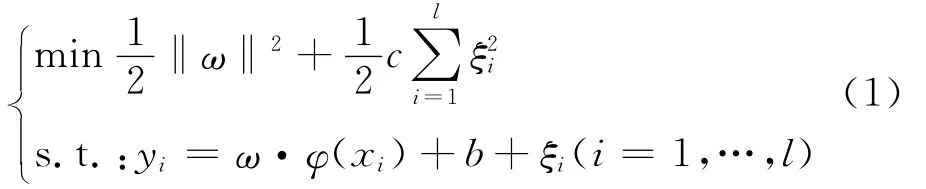
建立Lagrange函数优化上述问题：

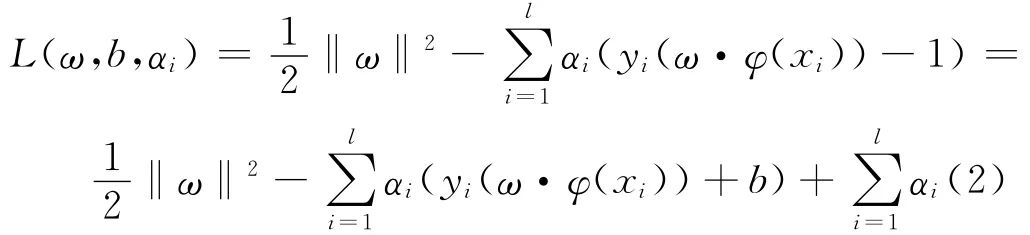
式中，ai＞0.那么以上问题就变为

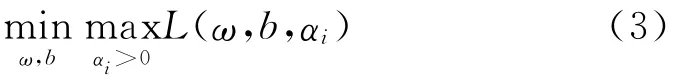
根据 KKT（Karush－Kuhn－Tucker）条件：

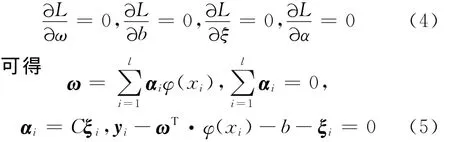
定义核函数k（x，xi）满足 Mercer条件，消去ξi和ω后，ξi和ω得到如下线性方程组：

式中：e＝［1，1，…，1］T；I为单位矩阵；α＝［α1，α2，…，αl］T；Qij＝K（xi，xj）；i，j＝1，2，…，l.

就核函数而言，能作为核函数的需满足Mercer条件.较为常用的核函数有如公式（7）所示的径向基核函数（RBF）：

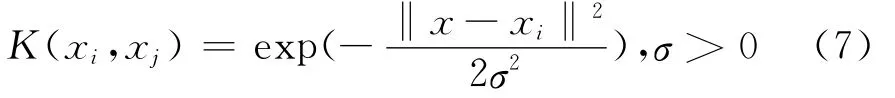
最后得到的回归模型如下：

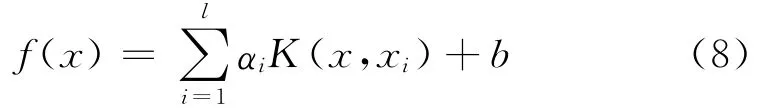
综上所述，SVM回归模型的关键在于惩罚因子c和核参数σ的选定，本文通过SDCS算法对参数c和σ进行全局寻优.

2 基于最速下降法的混合布谷鸟搜索算法

2.1 算法

Yang和Deb通过模拟布谷鸟随机寻找适合自己产卵的位置的特点，抽象出了布谷鸟搜索算法［7］.以下3条规则为布谷鸟搜索算法的前提：

规则1：每只布谷鸟每次只产一个卵，并随机选择鸟巢进行孵化［8］.

规则2：每次用于产卵的随机鸟巢中，产出最好蛋的鸟巢将会被存放至下一代.

规则3：可用于产卵的鸟巢总数n是一定的，称鸟窝主人发现鸟巢中含有外来蛋的概率为发现概率pa，则发现概率满足pa∈［0，1］.

在布谷鸟搜索算法中，每个随机的鸟巢都与每个最优解一一对应.第一步，基于当前解的基础之上，布谷鸟搜索以Levy flights的随机游动产生新解，评估完成后以最大限度的选择较优解.其次，根据发现概率pa放弃部分解以增加多样性.最后，采用偏好随机游动方式重新生成与被放弃解数量相同的新解，评价和保留较优解之后，完成一次迭代［9］.

当Levy flights组件生成新解后，代入式（9）生成F－化解Xt＋1，i：

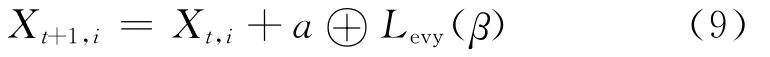
式中，α表示步长信息，Xt，i表示第t代第i个解.α用于确定随机搜索范围：

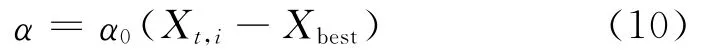
其中，α0是常数（α0＝0.01），Xbest表示当前最优解.

公式（9）中，⊕表示点乘积（entry－wise multiplications），Levy（λ）服从Levy概率分布：

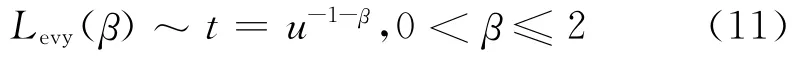
为方便计算，采用公式（12）计算Levy随机数：

其中，u，v服从标准正态分布，β＝1.5.

显然，归纳公式（9）～（13），在 Levy flights游动组件中，新解Xi的产生可通过公式（14）进行计算

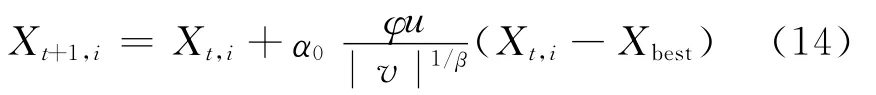
下面以发现概率pa放弃部分解.通过公式（15），布谷鸟搜素算法采用交叉操作和混合变异方式重新生成若干等数量的新解：

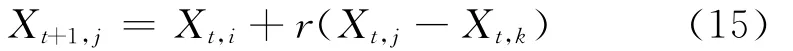
其中，r为（0，1）上均匀分布的随机数，称为缩放因子；Xj和Xk表示两个随机解.

2.2 SDCS算法

最速下降法作为最悠久的优化算法之一具有简单直观，有一阶收敛速度，目前更为行之有效的优化算法均建立在该算法的基础之上.为克服布谷鸟搜索算法之前所述的缺陷，利用最速下降法进行迭代修正，其迭代流程可按以下步骤表示：

第1步：选定初始点x0，预先给定停止误差ε＞0，令k：＝（）；

第2步：计算▽f（xk），若‖▽f（xk）‖≤ε，跳出迭代，输出xk.反之进行第3步；

第3步：取pk＝－▽f（xk）；

第4步：进行一维搜索，求tk，使得：

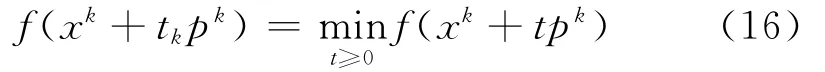
令xk＋1＝xk＋tkpk，k：＝k＋1转第2步.

通过布谷鸟搜索算法而保留得到鸟类孵出上代的最优解，并利用最速下降法简单灵活、善于解决n元函数的无拘束非线性规划问题的优点进行迭代，不断修正最优鸟巢的位置，最终获得最优解矩阵.

3 大坝变形SDCS－SVM预警模型建立

综合上述理论，大坝变形SDCS－SVM预警模型的流程图如图1所示.

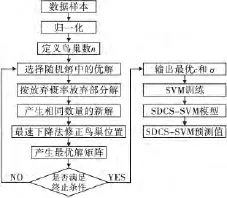
图1 流程图

4 实例分析

4.1 SDCS－SVM 模型建立

西南某混凝土双曲拱坝，坝顶高程1 245m，最大坝高293.5m，总装机容量420万kW.对其布置正垂线对大坝变形进行监测，选取大坝拱冠梁测点的监测资料，其中20100701～20120524共100组实际观测数据用于拟合，20120531～20120719共8组观测值用来预测.

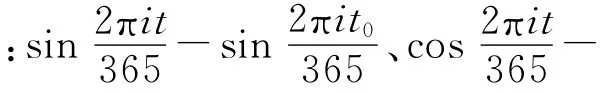
为加快学习的速度，需要标准化训练样本的数据.每组样本数据的最大、最小值用Xmax、Xmin表示，则标准化后变量如公式（17）所示：

下面定义鸟巢总数n＝25，发现概率pa＝0.25，最大迭代限制次数为100次，惩罚因子c的变化范围为［0.1，100］，核参数σ的变化范围为［0.01，10］.通过Matlab数学软件比较SDCS－SVM模型与多元回归模型的拟合以及预测情况.经过SDCS算法的寻优，支持向量机最优的惩罚因子c为0.998 4，核参数σ为0.987 5.

4.2 模型的比较分析

为了更为直观的展现SDCS－SVM模型拟合值的优越性，将其与多元回归模型的拟合值进行比较，如图2所示.

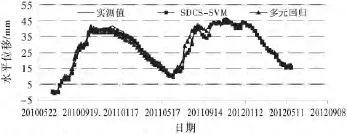
图2 模型拟合曲线图

图3为SDCS－SVM模型与多元回归模型预测值的比较.从图中可以清晰的看出，SDCS－SVM模型的预测精度高于多元回归模型.

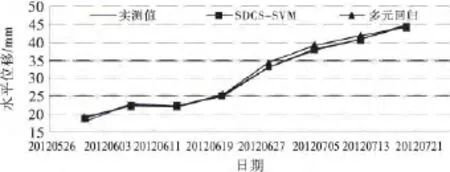
图3 模型预测曲线图

下面利用均方差（FMSE）来比较不同模型的拟合和预报精度，均方差越小表示拟合预测的精度也就越高.公式（18）为均方差的计算公式：

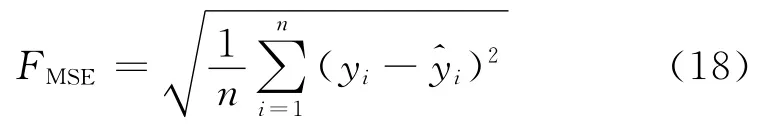
式中，n为样本数；yi为监测实值为模型计算值.SDCS－SVM模型、SVM模型、多元回归模型的拟合时段、预测时段的均方差见表1所示.

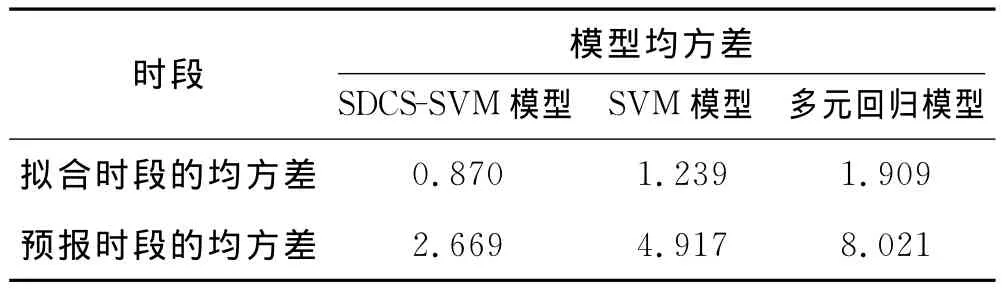
表1 模型均方差比较

从3种模型的拟合效果来看，SDCS－SVM模型效果最优，SVM模型效果其次，多元回归模型效果最差.从模型的预报效果来看，SDCS－SVM模型的泛化能力最好，多元回归模型的泛化能力最差.

5 结 论

为避免布谷鸟搜索算法在后期搜索速度过慢和搜索精度过低的缺陷，将其与最速下降法相结合，提出了基于最速下降法的布谷鸟搜索混合算法.再将其与支持向量机相结合，形成SDCS－SVM模型，并在大坝监测数据的拟合与预测上进行运用.从分析实例可以看出，SDCS－SVM预警模型相对于SVM模型和多元回归模型，具有更好的非线性拟合能力和泛化能力，可用于复杂的大坝安全非线性预警模型的建立.

［1］ 苏怀智，吴中如，戴会超，等.初探大坝安全智能融合监控体系［J］.水力发电学报，2005，24（1）：122－126，52.

［2］ Su Huaizhi，Hu Jiang，Wu Zhongru.A Study of Safety Evaluation and Early－warning Method for Dam Global Behavior［J］.Structural Health Monitoring，2012，11（3）：269－279.

［3］ 姜翠萍.支持向量机模型和算法研究［D］.大连：大连理工大学，2005.

［4］ 杜利敏，阮 奇，冯登科，等.基于共轭梯度的布谷鸟搜索算法［J］.计算机与应用化学，2013（4）：406－410.

［5］ 苏怀智，温志萍，吴中如，等.基于SVM理论的大坝安全预警模型研究［J］.应用基础与工程科学学报，2009，17（1）：40－48.

［6］ 李方方，赵英凯，颜 昕，等.基于Matlab的最小二乘支持向量机的工具箱及其应用［J］.计算机应用，2006，26（z2）：358－360.

［7］ 王 凡，贺兴时，王 燕，等.基于高斯扰动的布谷鸟搜索算法［J］.西安工程大学学报，2011，25（4）：566－569.

［8］ 吴 炅，周健勇.整数规划的布谷鸟算法［J］.数学理论与应用，2013（3）：99－106.

［9］ 胡欣欣，尹义龙.求解连续函数优化问题的合作协同进化布谷鸟搜索算法［J］.模式识别与人工智能，2013（11）：1041－1049.