钢管砼系杆拱桥模态参数识别及有限元仿真

于国军 陈灯红 操礼林 孙 虎

（1.江苏大学 土木工程与力学学院，江苏 镇江 212013；2.三峡大学 土木与建筑学院，湖北 宜昌 443002）

钢管砼系杆拱桥以纵梁作为拉杆，钢管砼拱与纵梁在拱脚处刚结，拱梁共同承受外部荷载，受力上类似于简支梁.它具有结构轻、跨度大、节约建材、结构形式简洁美观的优点，因此，近年来这种结构被广泛应用于公路工程［1］.

随着跨径的增大，作为主要受力构件的钢管砼拱肋、桥面纵梁和吊杆的强度、刚度和稳定性对全桥的结构安全至关重要.虽然采用钢管砼提高了拱桥的刚度，但是其重心高，自重大，钢管砼拱肋与桥面纵梁一般采用柔性吊杆连接，导致车辆荷载作用下振幅大，结构易发生下挠、开裂和结构的整体刚度下降等病害［2］.因此，对钢管砼系杆拱桥进行定期的健康监测是保证其在设计寿命有效期的安全运行的重要手段.本文以宁杭高速南河特大桥主桥—钢管砼系杆拱桥为研究对象，采用大型有限元软件ABAQUS建立桥梁结构的初始有限元模型，并利用环境激励下桥面的动力响应信号进行全桥的动力特性参数识别，结合实测的吊杆内力、桥梁线型等相关数据对桥梁结构有限元分析模型进行修正，而模拟结果也可以弥补实际监测数据的不足，最终建立适用于钢管砼系杆拱桥结构的有限元模型修正实用方法，服务于该桥梁的健康监测、状态评估［3－4］与损伤识别.

1 工程背景

学八路南河特大桥位于溧阳市新昌镇和蒋店镇交界处，为预应力砼系杆拱结构，采用刚性系梁刚性拱，计算跨径L＝126.28m，拱轴线为二次抛物线，矢跨比为1／5，矢高25.256m.设计荷载：汽车—超20级、挂车－120.拱肋均为钢管混凝土结构，上、下行线均独立成桥，每孔桥由两片钢管混凝土拱肋承重，主桥共有4片拱肋，拱桥全跨系杆设19组吊杆，每组两根吊杆吊起横梁两端与系梁搭接处.横梁为后张法预应力钢筋混凝土带牛腿矩形截面梁，系梁为后张法预应力钢筋混凝土箱形截面梁.在拱脚处，端横梁、拱肋和系梁固结.主桥下部结构为钢筋混凝土矩形墩、钻孔灌注桩基础，分离式承台.桥梁结构如图1所示，现场照片如图2所示.

图1 南河特大桥立面布置

图2 南河特大桥现场照片

2 基于环境激励的模态参数识别

由风荷载、车辆荷载、冲击波等环境激励引起的桥梁振幅扰动较小，但是其响应所涵盖的频率丰富.在进行桥梁结构的模态参数识别时，既不干扰桥梁正常运行，也不需要增加特殊量测设备，只要将桥梁响应数据测量出即可进行模态参数的识别［5－7］.其识别出的参数更符合实际情况和边界条件，并且实现对桥梁的实时安全和损伤检测.

峰值拾取法［8］（Peak Picking，PP）是基于结构的频响函数在固有频率处会有峰值的一种模态识别方法，环境激励下的桥梁振动响应的功率谱代替频响函数.此时，模态特征频率由平均正则化了的功率谱密度曲线上的峰值确定.

2.1 峰值拾取法基本理论

对于多自由度阻尼系统，系统振动的动力学方程为

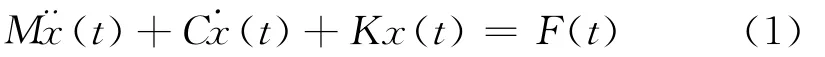
系统满足初始状态x（0）＝0，˙x（0）＝0，对式（1）做Laplace变换可转化为

式中，H（s）为传递函数.如果令s＝jω，则上述变换过程等同于傅里叶变换过程，传递函数H（s）就是频响函数：

上式进一步分解可得：

式中，N为模态阶数；φir、φkr分别为第r阶模态的振型在i和k点处的振型矢量；λr和分别为结构的一对共轭特征值.

结构上任意一点i的动态位移响应xi（ω）可以用k点激励力fk（ω）和结构频响函数Hik（ω）表示：

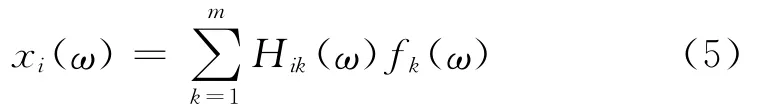
环境激励可以近似为白噪声，即功率谱密度函数在所有的频率范围内近似均匀分布，则结构上各处的输入满足：

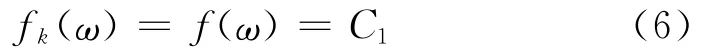
式中，C1为一个常数.因此，式（5）可简化为

由上式可知，结构的响应xi（ω）和结构系统的总频响函数是等价的，因此可以直接由相应谱xi（ω）得到结构的固有频率.

选择桥梁上的一个点作为参考点，建立响应点与参考点之间的传递率来识别结构系统的模态振型（结构的工作挠度）.响应点与参考点之间的传递率为

式中，αi（ω）为结构频率为ω时的变形情况，可近似看作系统的模态振型.将式（7）代入上式有：

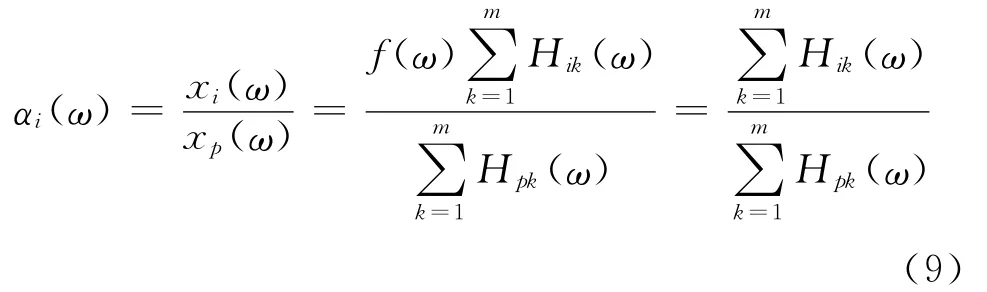
假定结构的各阶模态之间不存在耦合或者耦合度很小，那么由式（4）和式（9）可得：

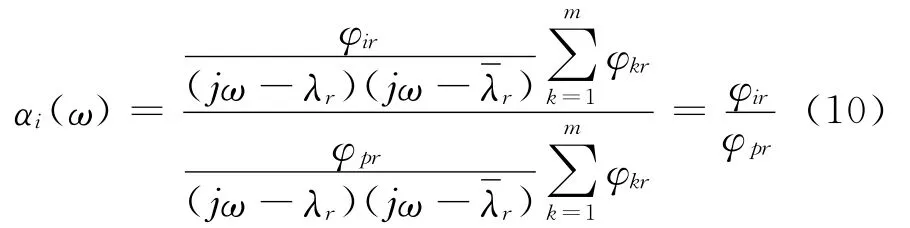
式中，由于点p作为参考点是固定的，因此对于一个确定的固有频率ωr处，φpr是一个定值，则上式简化为

可知：结构在频率ωr处的模态振型可通过读取传递率曲线αi（ω）直接得到.振型的大小可由传递率在固有频率处的幅值得到，此频率处的振型方向可由互功率谱在该处的相位或传递率实部的符号得到.

结合上述理论，桥梁的模态参数完全可以在不知道激励输入的情况下，利用测点之间的自、互功率谱，结合互谱相位、传递率等来估计得出，模态分析的精度取决于参考点的选择，以及数据采集的长度，数据分段大小和数量等因素.

2.2 钢管砼系杆拱桥桥面模态参数识别

根据峰值法的模态参数识别理论，钢管砼系杆拱桥桥面模态参数可以仅利用桥面的振动响应来识别［9］.根据系杆拱桥的一般振动特性，每跨桥布置7个测点，由于上、下行线均独立成桥，并完全相同，所以选取其中的下行桥进行测试，测试设备为891型拾振器、941型拾振器、东华DH5920动态数据采集系统，941型八线放大器.每个测点布置1台垂直拾振器和1台水平拾振器.测点布置如图3所示.

图3 桥面振动测点布置图

在测试系统安装、调试并校准之后，进行测试，在采集过程中，为了使信号在进行模态分析时更具一般性，要求每个测点采集时间在30min左右.模态参数识别的主要步骤如下：

1）构建钢管砼系杆拱桥桥面模型.

2）桥面节点赋值：建立数据文件，导入所采集的模态数据，并对模型的每个节点进行赋值，对于测点赋予测量的真实值，对于非测点，则由测点值对其进行插值.

3）选取峰值点：对数据进行FFT变换.由于模态测试中每个测点的数据采集时间为1 800s左右，采样频率50Hz，总共约90 000点数据，采用可以有效地减小信号泄漏的汉宁窗（hanning）函数进行加窗处理.可以得到自、互功率谱幅值、相位、相干函数、传递率，根据功率谱上的峰值确定桥梁的自振频率.

4）真实模态判别：构造模态置信因子矩阵，若为真实模态，则该矩阵中非对角元素应接近为0.根据该准则，桥梁垂直方向振动的固有频率为0.89Hz、1.75Hz和2.48Hz.其振型如图4所示.

图4 拱桥桥面振型图

3 拱桥有限元模型修正

利用大型有限元结构分析软件ABAQUS，并依据设计图纸建立钢管砼系杆拱桥的空间有限元模型.为提高数值模型的计算精度，数值建模采用杆单元与实体单元同时应用在计算模型中的鱼刺模型来模拟该拱桥［10］，并且模拟了桥梁的真实箱梁结构.主拱圈和吊杆均采用杆单元来模拟，桥面和拱脚采用六面体实体单元来模拟，模型总结点数是72 211，单元数是56 012，六面体实体单元数是54 800，杆单元数是1 132，如图5所示.

图5 钢管砼系杆拱桥有限元计算整体模型

由于拱桥中吊杆张紧力的大小对全桥的线性及振动特性都有很大的影响，为保证计算结果的可靠性，通过降温法将试验实测的索力施加到对应的吊杆上.吊杆内力采用振动法检测，即对拉索进行瞬时激振，用振动传感器测量出拉索的自振频率，由理论公式计算拉索的内力.振动检测设备为德国POLYTEC公司生产的激光测振仪PDV100.南河特大桥的吊杆平面如图6所示，其测试得到的吊杆力分布如图7所示.

图6 吊杆平面示意图

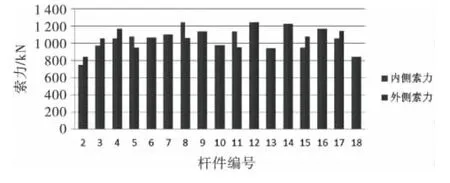
图7 吊杆力分布图

将所识别的桥面模态参数以及测得的吊杆内力结果与有限元计算的动力特性结果进行对比，修正钢管砼系杆拱桥的有限元模型，调整相关材料的参数与模型边界条件.本文选择将桥梁计算的频率和其识别值的相对误差最小作为目标，将有限元模型修正转化为优化问题进行迭代求解.通过修正计算，拱桥的自振频率见表1.拱桥的第一、第二、第三及第六振型如图8所示.

表1 拱桥的自振频率

图8 拱桥桥面仿真振型图

由表1及图4与图8的对比可知：拱桥有限元模型经修正后，其自振频率与模态识别的结果比较一致，第二阶频率与模态识别出频率相差9.0%，第三阶频率相差18.9%，第六阶频相差15.7%；有限元模型的第二、第三和第六阶振型与所识别出的第二、第三和第六阶振型比较一致.由于桥面布置的测点均沿桥面纵向布置，现场实测中对于第一、第四、第五阶的沿桥梁横向的垂直向振型和扭转振型未能有效识别.

4 结 论

通过现场测试和有限元仿真相结合的方法对南河特大桥主桥—钢管砼系杆拱桥进行模态参数识别及模型修正，结果表明：①峰值法简单迅速，且物理意义明确，适于分析环境激励下结构的模态参数，可得到比较精确的频率和振型结果；②经修正后的模型能更准确地反映结构的动力特性，可作为桥梁结构健康监测中损伤识别与安全评估研究工作的基准模型.

［1］ 林 伟，杨小旺，殷新锋，等.下承式钢管砼系杆拱桥缆索吊装系统分析［J］.公路与汽运，2015，166：159－164.

［2］ 高丽鹤.钢管混凝土拱桥健康监测系统研究［D］.郑州：郑州大学硕士学位论文，2014.

［3］ Li Zhijun，Li Aiqun，Han Xiaolin.Operational Modal I－dentification of Suspension Bridge Based on Structural Health Monitoring System ［J］.Journal of Southeast U－niversity（English Edition），2009，25（1）：104－107.

［4］ Vu V H，Thomas M，Lakis A A，et al.Identification of Modal Parameters by Operational Modal Analysis for the Assessment of Bridge Rehabilitation［C］.Proceedings of the 2nd International Operational Modal Analysis Conference，IOMAC 2007.

［5］ 韩建平，郑沛娟，骆勇鹏，等.一刚构－连续组合梁桥在环境激励下的模态参数识别［J］.工程力学，2013，30：99－103.

［6］ 樊江玲.基于输出响应的模态参数辨识方法研究［D］.上海：上海交通大学博士学位论文，2007.

［7］ Gentile C.Modal and Structural Identification of a R.C.Arch Bridge［J］.Structural Engineering and Mechanics，2006，22（1）：53－70.

［8］ Ren Wei－Xin，Zatar Wael，Harik Issam E.Ambient Vibration－based Seismic Evaluation of a Continuous Girder Bridge［J］.Engineering Structures，2004，26（5）：631－640.

［9］ 叶锡钧，颜全胜，李 健.基于环境激励的大跨度斜拉桥模态参数和索力识别［J］.振动与冲击，2012，31（16）：157－163.

［10］张国栋，朱 暾，张 峰.梁－拱共同工作的桥梁有限元分析［J］.三峡大学学报：自然科学版，2001，23（5）：410－412.