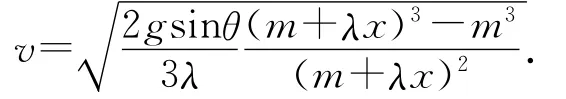百变柔软绳——质心运动定理的一个应用

郭 敏 王文涛 王庆勇

（1.东北师范大学物理学院，吉林 长春 130024 2.东北师大附中，吉林 长春 130024）

物理学致力于研究物质的基本结构及运动基本规律.在中学物理教学中，我们接触到的多是一个个诸如物块、小球等可视为质点的物体，对于生活中常见的绳子一般是作为某个或某几个研究对象的连接媒介出现，常常伴随的特点是质量可以忽略不计，一旦出现质量不能忽略的绳子，不仅学生无法解决，很多教师也对其束手无策.但是不得不承认这种有质量的绳子才是更贴合实际的，是每一个高中物理教师以及致力于物理奥赛的学生都有必要了解和掌握的.笔者结合自身经验对有质量的柔软绳问题设想了几种情况，现将其整理成习题，供大家一起探讨.

例.如图1所示，一质量为m、长为l的柔软绳两端竖直地悬挂在天花板上，某一时刻松开右端使其自由下落.求：在右端下落x时，天花板对左端的拉力T.

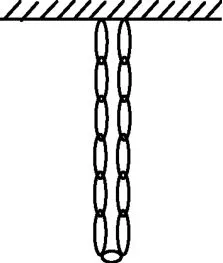
图1

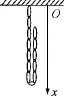
图2

方法1.质心运动定理的动量表达式.

其中

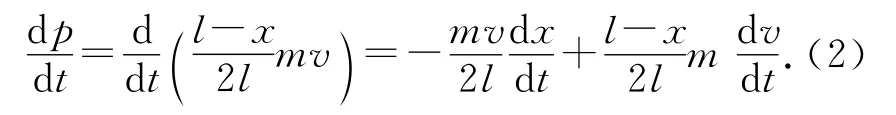
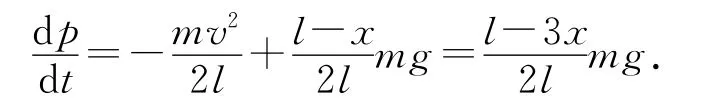
联立（1）、（3）式，得

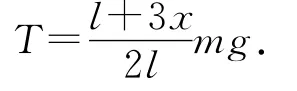
方法2.质心运动定理的加速度表达式.

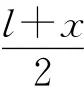
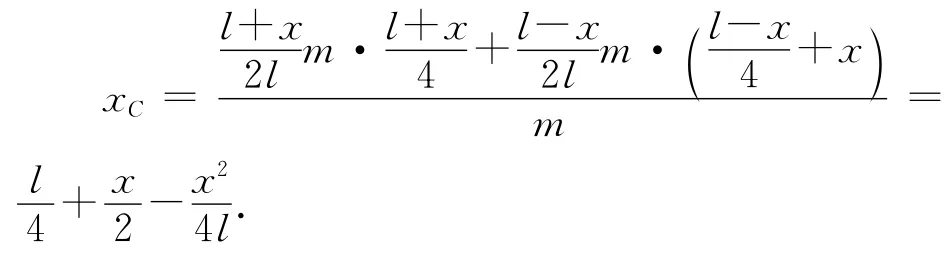
对质心坐标求一阶导数，有

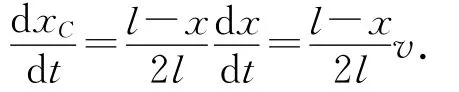
对质心坐标求一阶导数，有

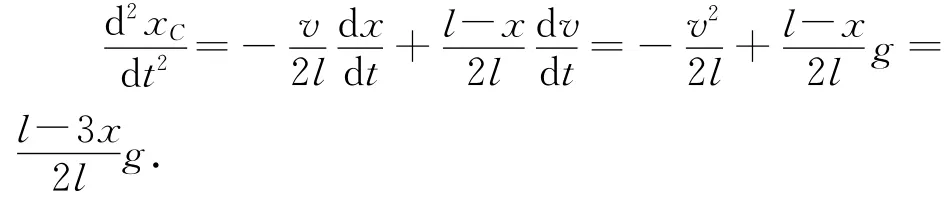
所以

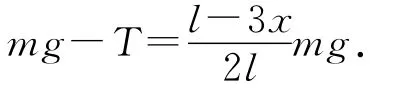
解得

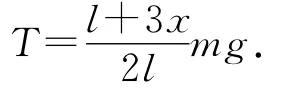
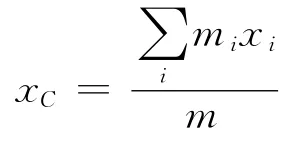
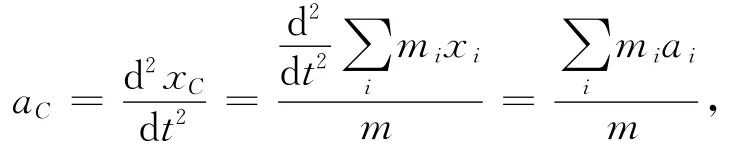
可用左右两侧绳子的加速度来求解整根绳子的质心加速度，即

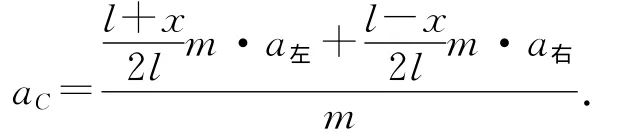
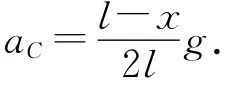
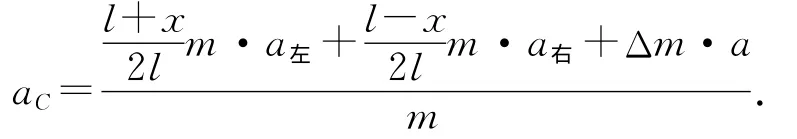
然而Δm和a都是不容易求出的，所以一般不选择此方法.

但是用质心坐标来计算质心加速度时，为什么没有考虑两侧接头处的微小质量呢？这是因为Δm所在处的位置坐标是有限值，一个无穷小乘以一个有限值，结果一定是无穷小.所以在利用质心坐标求质心加速度时可以忽略接头处的影响.如果绳子堆叠的形状不规则，质心坐标无法确定，我们也不能选用方法2来求解.因此解决此类问题最好的方法就是运用质心运动定理的动量表达式来求解，我们来看下面的例题.

图3

1 水平拉绳问题

如图3所示，单位长度质量为λ的柔软长绳盘在光滑水平面内，现用一水平力F作用于绳端，使绳端从静止开始以恒定加速度a运动，求拉力F的大小.

解析：以水平向右为正方向，当绳端向右运动x时，已运动部分绳子的动量为p＝λxv.以整根绳子为研究对象，根据质点系动量定理，有

其中

联立（1）、（3）式，得

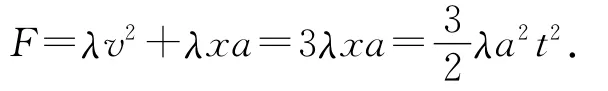
2 竖直落绳问题

一质量为m、长为l的柔软绳自由悬垂，下端恰与一台秤秤盘接触，如图4所示.某时刻放开柔软绳上端，求台秤的最大读数.

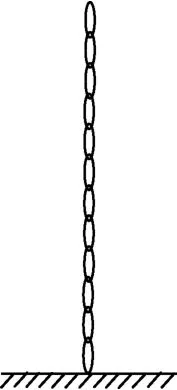
图4

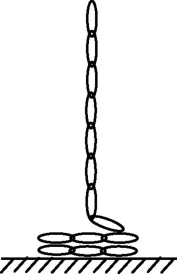
图5

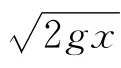
其中

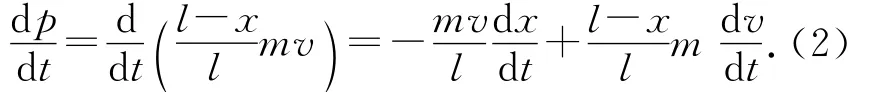
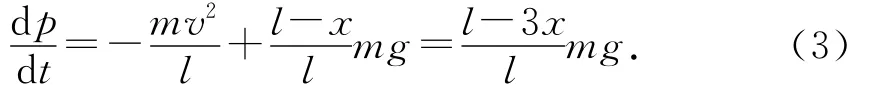
联立（1）、（3）式，得

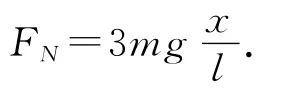
所以盘秤的最大读数为3mg，即出现在软绳将要全部掉到盘秤上时.

3 竖直抛绳问题

如图6所示，单位长度质量为λ的柔软长绳盘成一团置于地面上，绳的一端系着一质量为m球，若将球以初速度v0竖直上抛，球能上升多高？

解析：以竖直向上为正方向，当球上升x时，空中的绳子与球速度相等，将其视为一个整体，则动量为p＝（m＋λx）v.地上绳子的速度为0，动量为0.以整根绳子为研究对象，根据质点系动量定理，有

其中

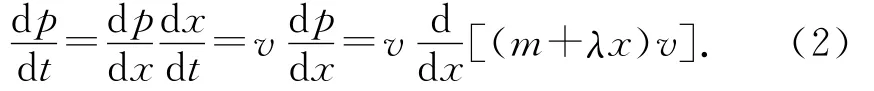
联立（1）、（2）式，得

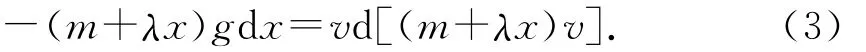
（3）式两边同时乘以（m＋λx），得

（4）式两边同时积分，得

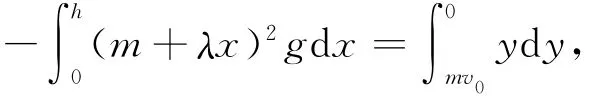
其中y＝（m＋λx）v.

解得

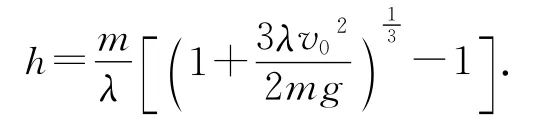
4 斜面滑绳问题

如图7所示，一质量为m的物体与单位长度质量为λ的柔软绳相连.开始时，物体静置于倾角为θ的光滑斜面的顶端，而柔软绳则盘放在斜面顶端边的平台上.释放物体，让其沿斜面滑下.求当它下滑距离为x时的速度v.

解析：以沿斜面向下为正方向，当物体下滑距离为x时，随物体下滑部分绳子与物块速度相等，将其视为一个整体，则动量为p＝（m＋λx）v.斜面顶端部分绳子的速度为0，动量为0.以整根绳子为研究对象，根据质点系动量定理，有

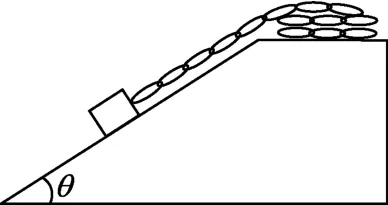
图7

其中

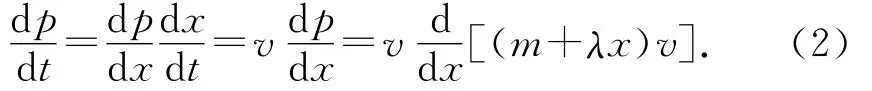
联立（1）、（2）式，得

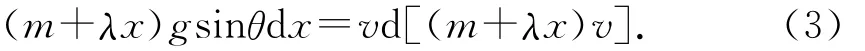
（3）式两边同时乘以（m＋λx），得

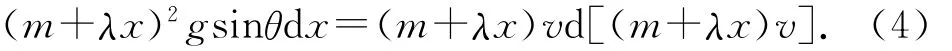
（4）式两边同时积分，得

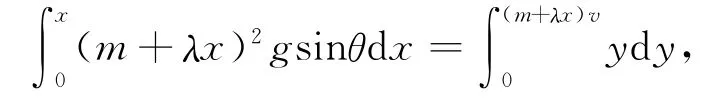
其中y＝（m＋λx）v.

解得