基于LS-DYNA的深沟球轴承动态仿真分析
2015-07-25刘江山宋丽陆超
刘江山,宋丽,陆超
(上海市轴承技术研究所,上海 201801)
球轴承是精密的机械零件,转动过程中各零件之间的力学关系复杂,对滚动轴承进行动力学分析和数值模拟研究已成为趋势[1]。随着计算机技术的发展,运用CAE技术对球轴承进行动态仿真,已经成为球轴承产品设计、制造、分析以及检测等领域不可缺少的工具,具有一定的工程意义。
1 动态特性仿真分析的基本理论
1.1 LS-DYNA动态仿真软件
文献[2]首先应用Hertz理论建立了球轴承的静力学分析模型,并推导出了钢球的最大承受载荷Qmax与径向载荷Fr的关系式。文献[3]中DYNA程序采用显式的中心差分格式,用于分析爆炸与高速冲击等过程中的大变形动态响应问题,该程序经过不断规范和完善,使得LS-DYNA程序系列的应用范围不断扩大,并建立起完善的软件质量保证体系,使其得到广泛使用,LS-DYNA程序的分析流程如图1所示。

图1 LS-DYNA分析流程图
1.2 LS-DYNA动态仿真基本理论
在求解滚动轴承动态特性仿真分析中,一般采用中心差分法,该方法不需要进行平衡迭代,也不需要直接求解切线刚度,因此求解速度快,节省计算时间[4]。
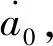
(1)
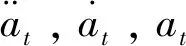
将位移at+Δt在t时刻进行Taylor展开,取最高的二次多项式,其近似值为
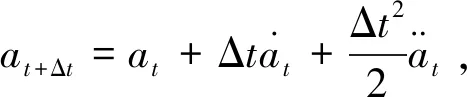
(2)
将(2)式进行求解后得到加速度与位移的关系为
(3)
速度与位移的关系为
(4)
将(3)式和(4)式代入(1)式可得中心差分法的经典公式为
(5)
由(5)式可知,若已知at-Δt和at,则可解出at+Δt,进而求出t时刻的速度和加速度。
2 有限元模型的建立
2.1 实体模型的建立
深沟球轴承是一种较具有代表性的滚动轴承,选择型号为608-2RS的深沟球轴承进行仿真分析,研究其转动过程中应力、应变场的变化以及振动情况,结构参数见表1。
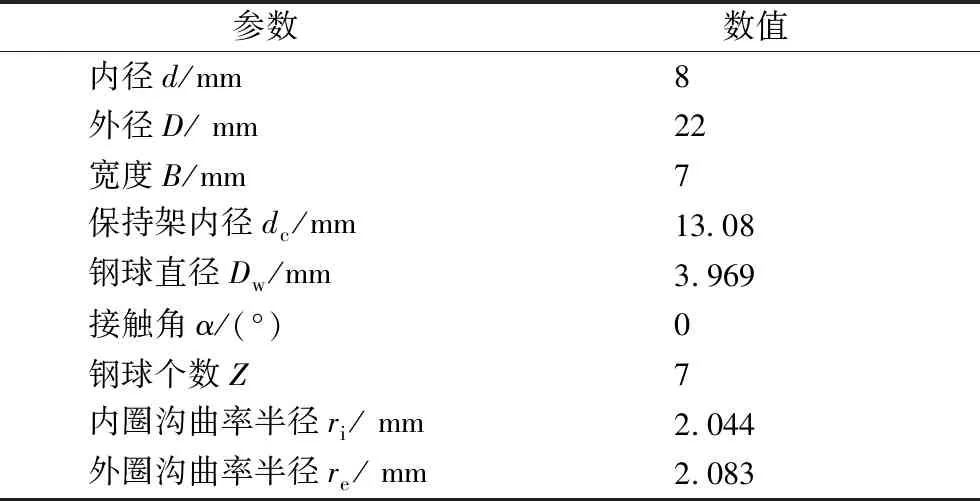
表1 608-2RS球轴承结构参数表
根据表中参数,在UG中建立球轴承三维实体模型,考虑到轴承实际模型的复杂性和现有计算机仿真的局限性,且轴承倒角、油膜等因素对整体动态特性影响很小,因此忽略轴承倒角、游隙以及密封防尘和润滑的影响。得到608-2RS深沟球轴承的三维实体模型如图2所示。
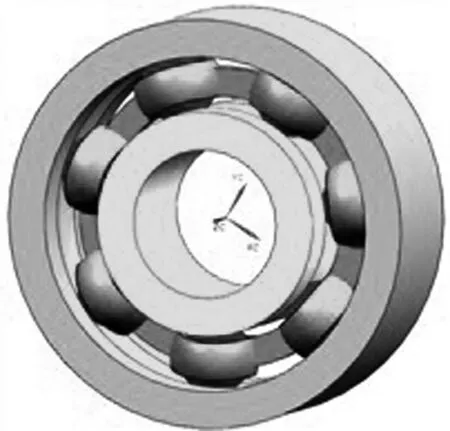
图2 608-2RS深沟球轴承三维模型图
2.2 有限元模型的建立
轴承实体模型导入LS-DYNA后,先定义显式单元Solid164和Shell163及其算法。定义内圈、外圈和钢球材料为GCr15,其弹性模量为208 GPa,泊松比为0.3;定义保持架材料为08F碳素钢,其弹性模量为219 GPa,泊松比为0.3。对内、外圈进行扫略划分网格,钢球进行映射划分网格,保持架进行自由网格划分,且钢球与保持架接触部位进行局部网格细化,有限元模型如图3所示。
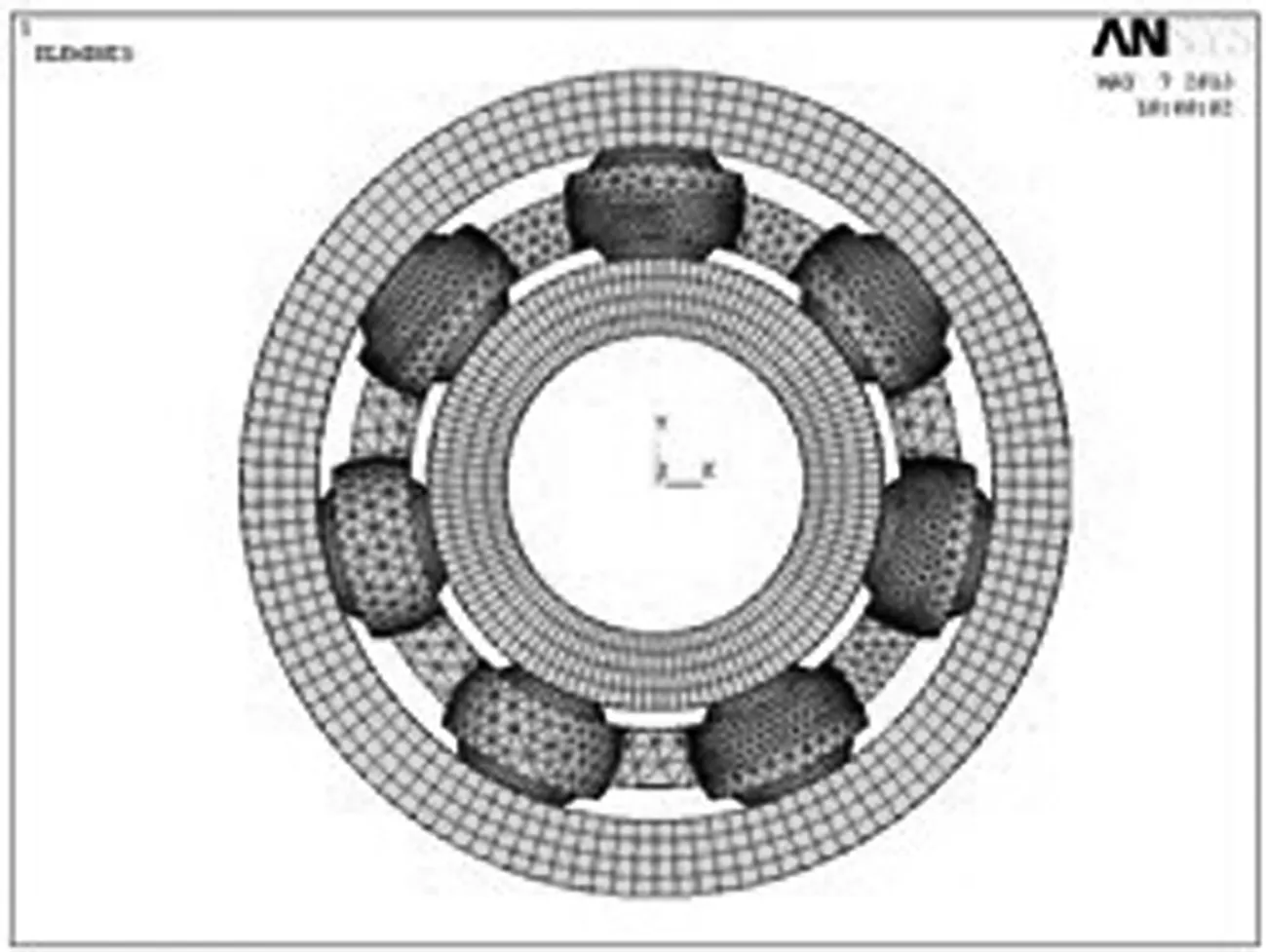
图3 608-2RS球轴承有限元模型
3 动态仿真及结果分析
假设轴承工作时承受的径向载荷Fr为500 N,轴承转速为1 800 r/min,为了模拟轴承实际承载过程,载荷施加在内圈下半部的刚性面上,转速施加在内圈刚性面上;在外圈外表面上间隔45°选取4个位置,分别对该位置上的节点施加x和y方向的移动约束以及x,y,z方向的转动约束,加载和约束后的有限元模型如图4所示。
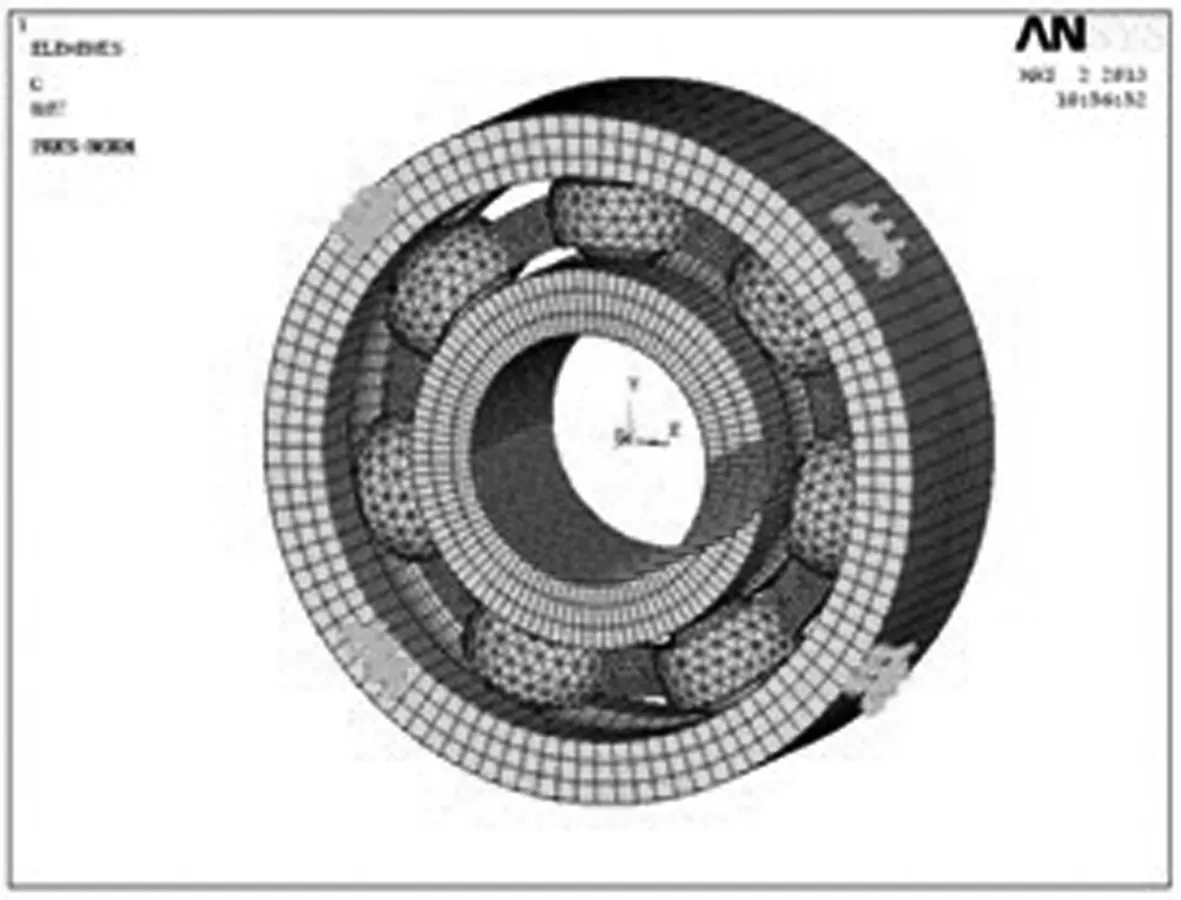
图4 加载和约束后的608-2RS轴承有限元模型图
3.1 等效应力分析
分别取4个时刻分析内圈速度和轴承应力,结果如图5所示。
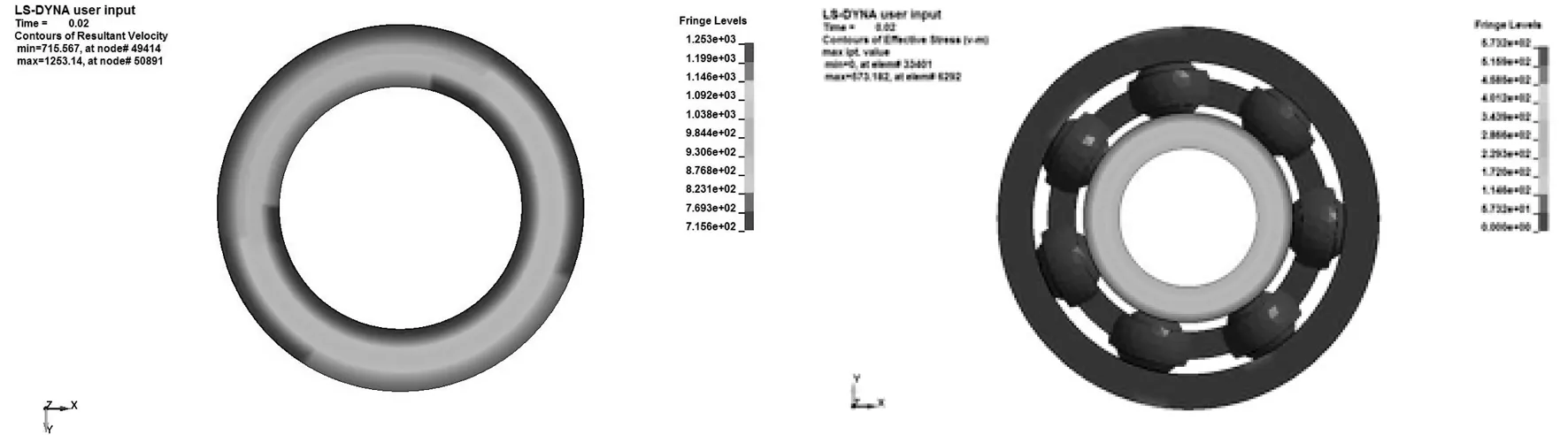
(a)0.02 s

(b)0.05 s
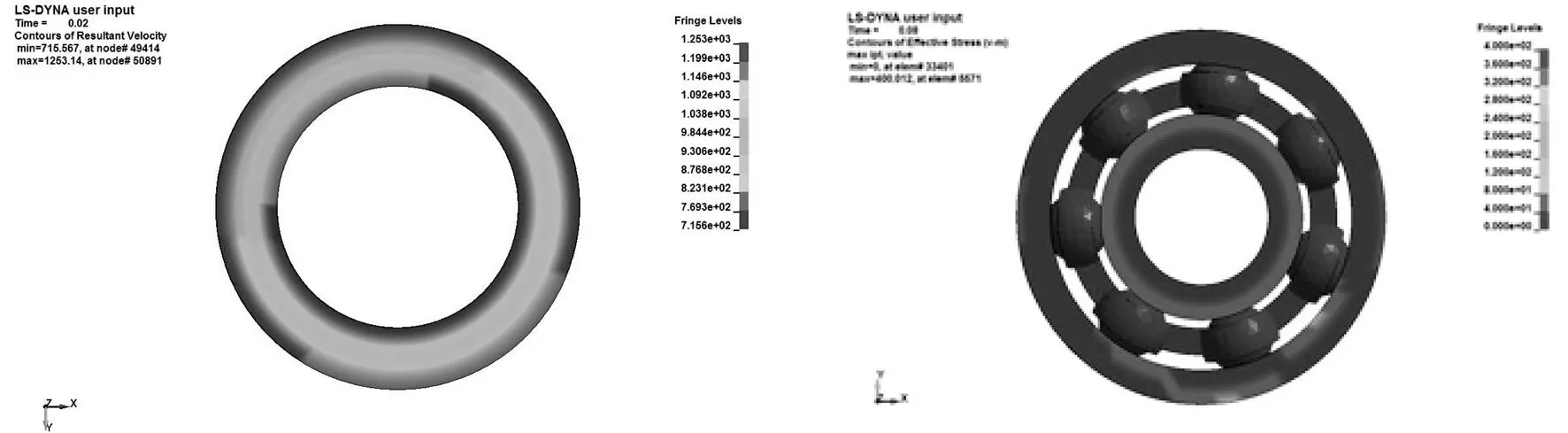
(c)0.08 s
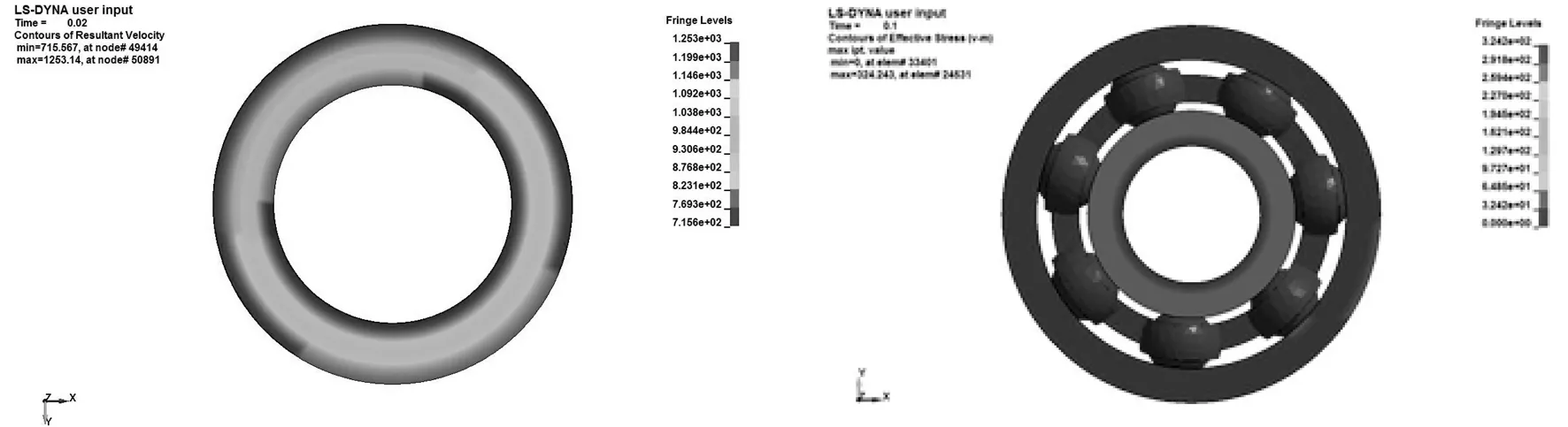
(d)0.1 s
由图5可知,在0.02 s时轴承承受的最大等效应力出现在内圈和轴的接触区域,其值为573.182 MPa;0.05 s时轴承承受的最大等效应力出现在钢球和内圈的接触区域,其值为496.063 MPa;0.08 s时轴承承受的最大等效应力出现在钢球和内圈的接触区域,其值为400.012 MPa;0.1 s时轴承承受的最大等效应力出现在钢球和外圈的接触区域,其值为324.243 MPa。钢球与内、外圈接触区域的应力较大,且最大应力值和其位置都会随着轴承的运转而发生变化。
3.2 切片应力云图分析
为了全面分析仿真过程中轴承内部的应力分布情况,对整个轴承进行切片处理,0.05 s时其应力云图如图6所示。

图6 0.05 s时轴承切片应力云图
由图6可知,最大应力出现在钢球和内、外圈接触表面以下的某一区域,并且其值由内向外逐渐减小,应力主要分布在轴承的承载区,承载区的应力明显大于非承载区,且应力分布区域呈椭圆形。
3.3 运动学分析
拾取钢球表面上的单元节点,绘制其沿x方向的速度时程曲线,结果如图7所示。
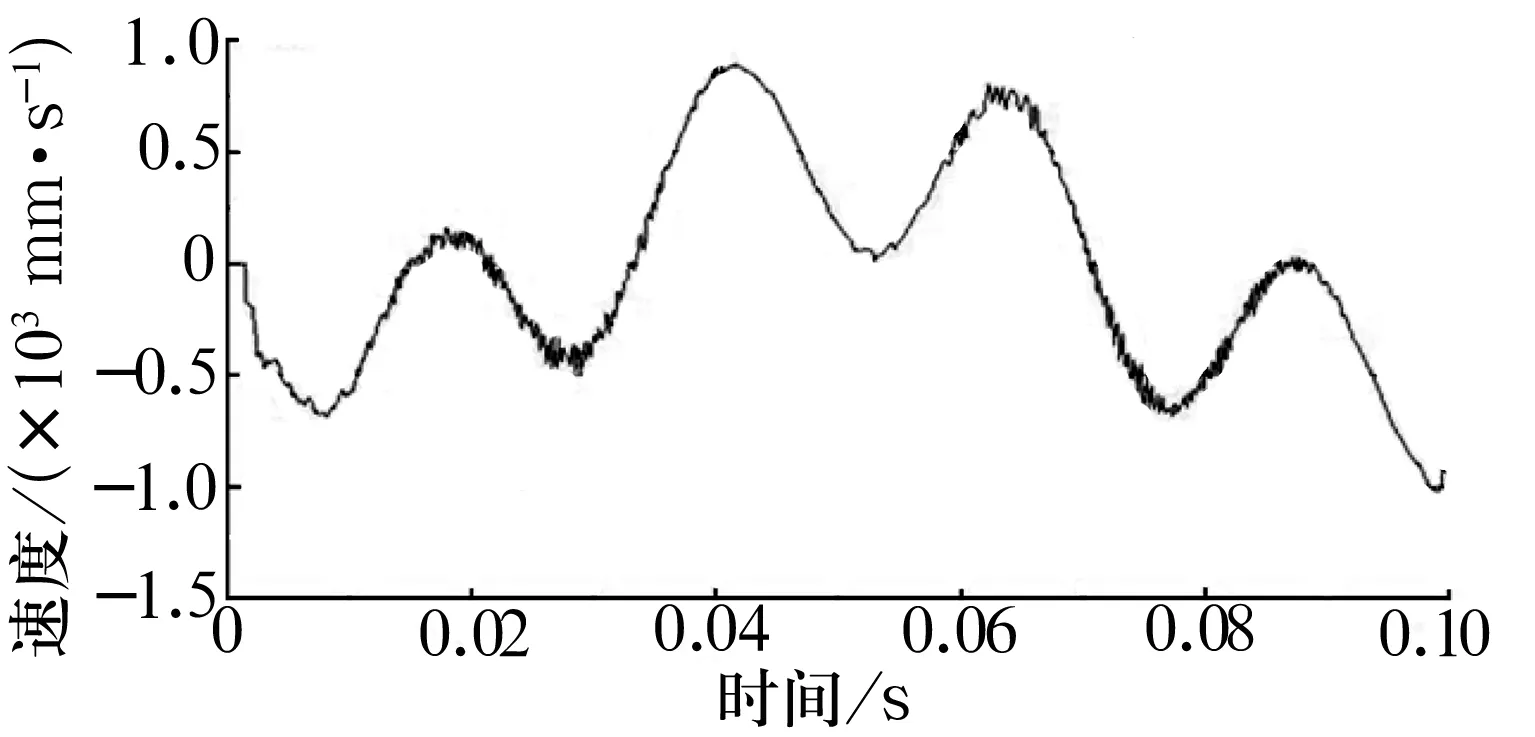
(a)沿x向的速度时程曲线
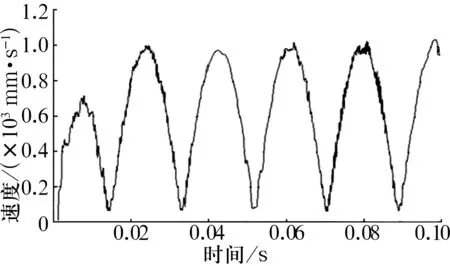
(b)综合速度时程曲线
由图7可以看出,钢球表面单元节点的速度曲线呈明显的周期性,周期约为0.037 5 s,单元节点在某些时刻附近x向的速度值为0,由于轴承在工作过程中内圈转动、外圈静止,此时钢球单元节点与内沟道接触时刻速度达到相应的最大值或最小值,与外沟道接触时刻速度为0,故此时钢球单元节点与外圈接触;该单元节点在0.043 s附近x方向的速度达到正的最大值为0.894 m/s,此时单元8节点与内圈下表面接触;单元节点在0.097 s附近x方向的速度达到负的最大值为-1.019 m/s,此时单元节点与内圈上表面接触。
根据上述分析,将提取的有限元结果与理论计算出的钢球自转角速度和质心线速度进行比较,结果见表2。

表2 线速度和自转角速度的理论值与仿真值
由表2可以看出,有限元解和数值解误差较小,表明采用ANSYS/LS-DYNA有限元法分析轴承的动态特征这一方法是可行的。
3.4 振动情况分析
为了反映轴承在转动过程中的振动情况,选取钢球接触区域的单元节点进行分析,其加速度的时程曲线如图8所示。
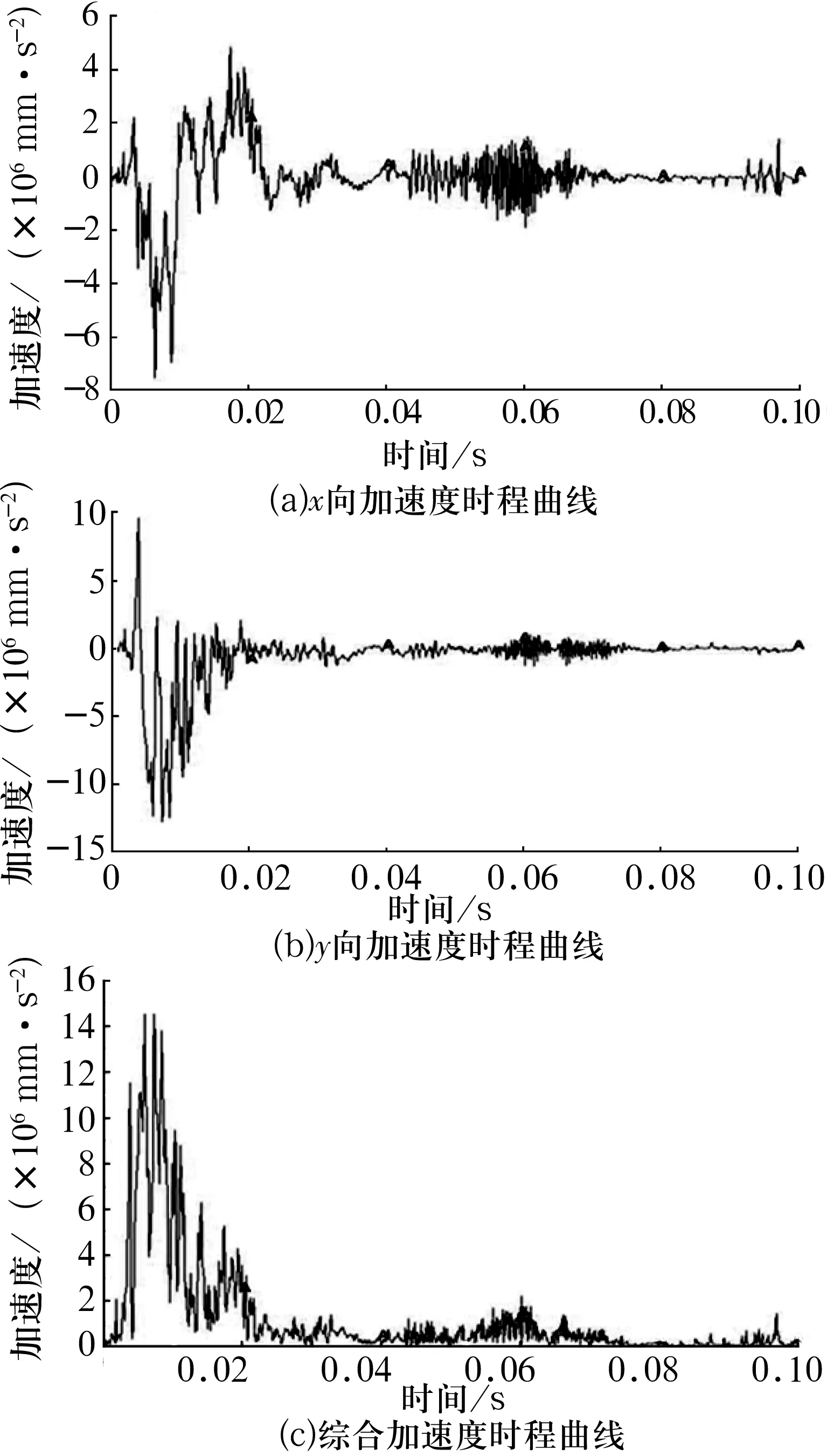
图8 接触区域钢球单元点加速度时程曲线
由图8可知,接触区域钢球上单元点在0~0.02 s加速度值波动较大,在轴承启动时,由于钢球受突加载荷的作用而产生强烈振动,而后又趋于缓和,但在0.06 s时钢球因受到突加转速的作用而使加速度值有小幅度的增加,轴承处于正常运转状态时,此节点处的加速度减小到约为零且趋于平稳变化状态。钢球加速度时程曲线没有明显的周期性,这种无规则的振动也说明轴承运转时产生较强的非线性特性,产生这种现象的原因是轴承在工作过程中产生非线性接触变形以及轴承元件运转时自由度的复杂性,同时由仿真可知,轴承的振动加速度随轴承转速的增大而增大。
3.5 实例应力计算对比
钢球承受的最大径向载荷为
(6)
将球轴承参数代入(6)式可得Qmax为357.14 N。
外圈、内圈以及钢球的曲率(凸面曲率值为正,凹面曲率值为负;下标xy,yz分别为轴向平面和径向平面)分别为

(7)

(8)

(9)
主曲率为
∑ρ=2ρw+ρxy+ρyz。
(10)
钢球与套圈接触椭圆的长、短半轴分别为
(11)
钢球与外圈接触时,代入相关参数可得主曲率∑ρ=0.417 9;利用插值法查询Hertz接触系数表可得接触椭圆系数ea=0.09,eb=0.01,εE=1。代入(11)式可得a=0.854 mm,b=0.095 mm。故最大接触应力Pemax= 3Qmax/2πab=986.8 MPa,平均接触应力Pem=Qmax/πab=657.87 MPa。
同理,钢球与内圈接触时,主曲率∑ρ=0.699 9,ea=0.106 6,eb=0.008 93,εE=1,a=0.852 mm,b=0.071 mm。最大接触应力Pimax=935.55 MPa,平均接触应力Pim=623.7 MPa。
钢球与内、外圈接触时应力的理论计算结果和有限元仿真结果见表3。由表可知,轴承应力的理论计算结果与仿真结果比较接近,验证了仿真的可行性。

表3 应力计算和仿真结果对比 MPa
4 结束语
文中以608-2RS型深沟球轴承为研究对象,首先运用建模软件UG建立了三维简化模型,再将其导入仿真软件LS-DYNA进行有限元分析,研究了深沟球轴承在运转过程中的接触应力、转速和振动的变化规律,通过与理论值的对比证明了仿真的可行性。
