关于内共振压电能量采集器
2015-07-25陈立群姜文安
陈立群, 姜文安
关于内共振压电能量采集器
陈立群a,b,c,姜文安b
(上海大学a.力学系,上海200444;b.上海市应用数学和力学研究所;c.上海市力学在能源工程中的应用重点实验室,上海200072)
内共振可以加强压电能量采集器.忽略电量的耦合,导出了内共振条件的解析表达式,与考虑电量耦合的精确情形相比,误差很小.数值计算输出电压的均方根表明,用该方法设计的内共振压电能量采集器在Gauss白噪声、2阶滤波产生的色噪声、窄带色噪声和指数相关色噪声激励下,都有良好的性能.
内共振;能量采集;随机激励
振动型能量采集器近年来成为研究热点[1],其中压电能量采集更受到广泛关注[2].振动型能量采集的工作原理是共振,因此只能采集特定频率成分的能量.如何使能量采集器在更广泛的外激励频率上工作成为改进能量采集效果的关键问题.解决该问题的一种途径是引入非线性,利用非线性振动系统的软特性或硬特性扩宽能量采集器工作频率范围,相关工作在文献[3]中有全面评述.这些工作都未涉及内共振的应用,而内共振也是非线性振动的突出特性.本文作者近期工作应用内共振的特性压电能量采集器[4]和磁电式能量采集器[5],分析内共振时,先要确定线性派生系统的频率,由此导出内共振时系统参数需要满足的条件.能量采集器系统的特点是机械量和电量互相耦合,因此只能用数值方法得到内共振时的特定参数[4],而无法得到内共振条件的显式表达.文献[5]中分析磁电式能量采集器时,忽略了电量耦合对频率的影响.本文研究压电式能量采集器,忽略电量耦合而得到内共振条件的解析表达式.与以往结果[4]比较,误差很小.数值仿真表明,在不同的随机激励下,该方法设计的内共振能量采集器比其他几种设计有更好的能量采集效果.
1 力学和数学模型
压电式振动型能量采集器如图1所示[4],以平衡位置为坐标原点,两个质量为m1和m2的物块相对于框架的位移分别为x1和x2,正方向向上,带压电环节的主质量m1通过刚度系数为k1的弹簧和黏性阻尼系数为c1的阻尼器与框架连接,主质量m1上还通过刚度系数为k2的弹簧和黏性阻尼系数为c2的阻尼器连接附加质量m2.3块磁铁,2块固定在框架上,1块固定在质量m1上,作用力方向如图1所示.压电部分,电阻、电容、输出电压和机电耦合系数分别为Rl、C、υ和θ.尽管系统的机械部分有2个自由度,但只有1个电回路,因此仍然是单模态的能量采集器.

图1 压电式振动型能量采集器Fig.1 Apiezoelectricvibrationbasedenergyharvester
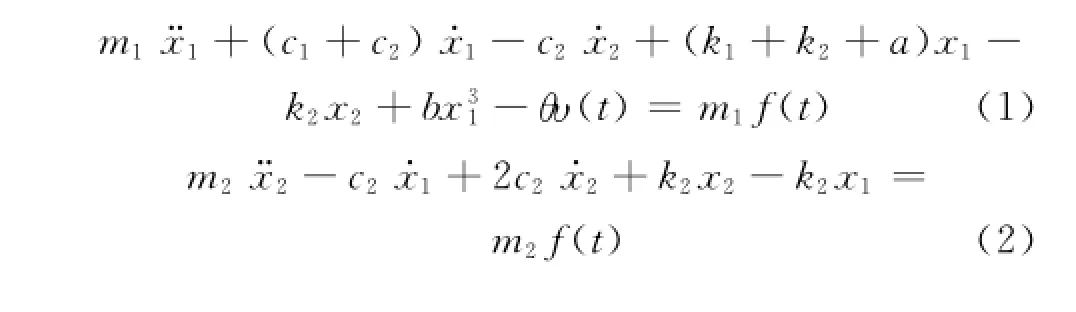

2 内共振条件
式(1)~(3)给出非线性振动系统,若该系统的线性派生系统固有频率成比例时,又可能出现内共振.在式(1)、(2)中略去非线性项、阻尼项和激励项,并忽略机电系统之间的耦合,得
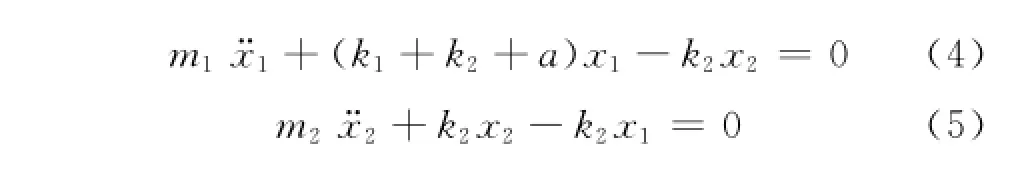
系统的频率方程为


即解得固有频率为
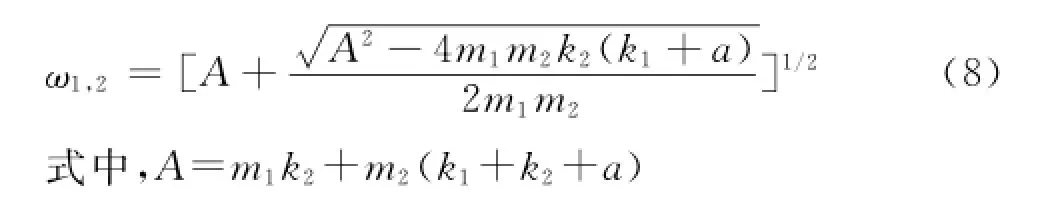
若有实数λ使得2个固有频率之间具有关系

则由式(8)可导出

3 不同类型随机振动的采集能量
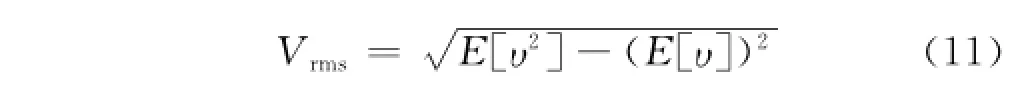
为说明内共振的优越性,在不同随机激励下计算压电能量采集器输出电压的均方根值:压电能量采集器考虑3种两自由度情形.固定参数m1=1.0,m2=0.2,k1=1.0,c1=0.01,c2= 0.005,a=1.0,b=0.5,θ=0.05,Rl=200和C= 0.1.两自由度情形,通过k2的选择使得2个固有频率ω2/ω1比为3和大于或小于3的无理数(见表1).作为比较,也考虑2种单自由度情形.1种不附加质量弹簧系统,即m2=0,k2=0,c2=0,此时ω1= 1.4142;另1种将质量m2直接固定在m1上,即质量由m1变为m1+m2,此时ω1=1.2910.
不忽略电量耦合时,文献[4]中得到了出现1∶3内共振所需要的参数值和相应的前2阶固有频率,两者比较如表2所示.因此忽略电量耦合产生的影响很小.
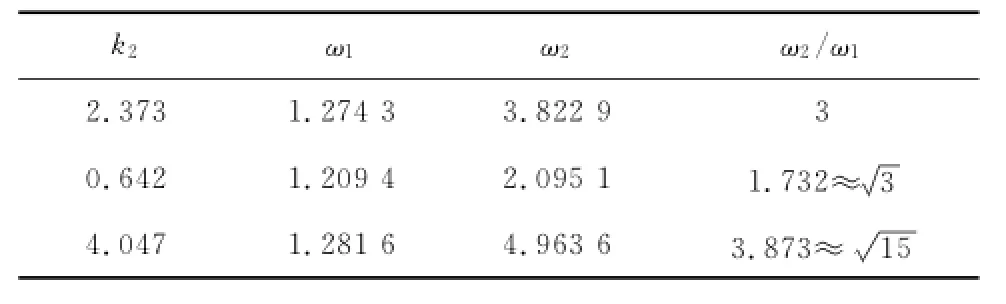
表1 两自由度能量采集器的不同参数Tab.1 Different parameters of the 2degreeoffreedom energy harvester
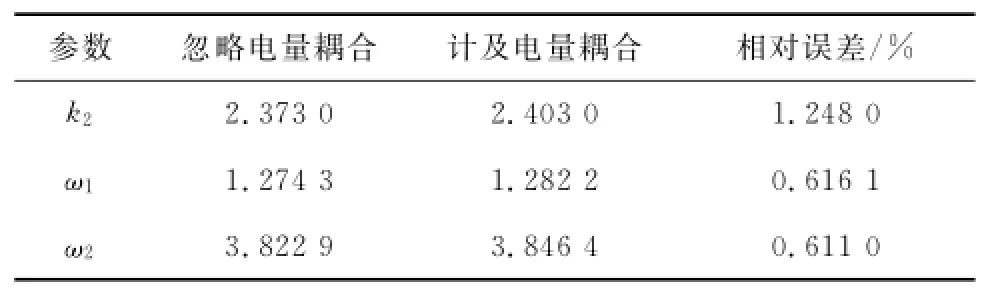
表2 电量耦合的影响Tab.2 The effects of electric coupling

数值仿真中,初始条件选为系统平衡位置,即)在给定初始条件下,可以用4阶Runge-Kutta法数值求解式(1)~(3).
3.1白噪声激励
基础激励为标准差为σf的随机激励f(t)[7].输出电压均方根值随标准差的变化如图2所示.当σf>0.07,内共振导致最大的输出电压.而当σf<0.07时,内共振的优势不明显.这可能是因为激励太小而不足以引发系统中的非线性效应.
3.22阶滤波定义的色噪声激励
色噪声随机激励f(t)由2阶滤波
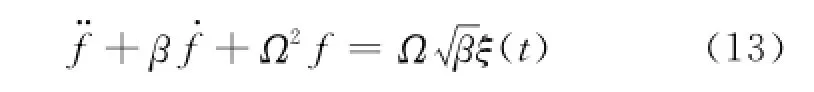
定义[8],式中:Ω为中心频率;β为带宽;ξ(t)为零均值和特定标准差σξ的白噪声.中心频率是影响能量采集的关键因素.当σξ=0.12和β=0.5时输出电压均方根随中心频率的变化如图3(a)所示,对于不同的设计,第1线性派生频率在1.274 3和1.414 2之间变化.由图可知,内共振产生的输出电压在靠近第1外共振,即1.0<Ω<2.0时远远大于其他设计,而且这一优点也保持到超过第2外共振,直到Ω=4.5.当Ω=2.0和β=0.5时输出电压随色噪声强度的变化如图3(b)所示,色噪声强度用式(13)中的白噪声ξ(t)的标准差表示σξ.结果表明,内共振导致最大的输出电压,只有在2个小区间[0.045,0.065]和[0.135,0.150]例外.带宽也影响输出电压,如图3(c)所示.除0.30和0.35之间的小带宽外,内共振导致最大的输出电压,特别是在0.6和0.9之间的带宽,优势更明显.

图2 不同参数下输出电压均方根随Gauss白噪声标准差的变化Fig.2 The averaged rootmeansquare output voltage versus the standard deviation of Gaussian white noise for different parameters
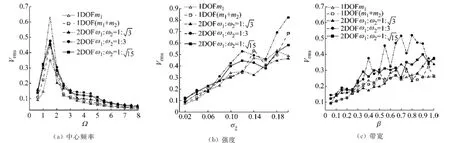
图3 不同参数下输出电压均方根随色噪声(13)中心频率、强度和带宽的变化Fig.3 The averaged rootmeansquare output voltage versus the center frequency,intensity and bandwidth of colored noise(13)for different parameters
3.3窄带噪声激励
考虑如下形式的窄带噪声激励[9]
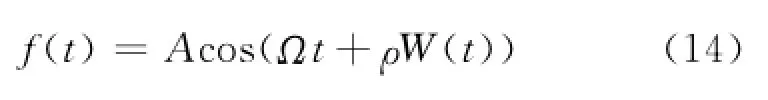
式中:A>0为确定性振幅;Ω为中心频率;ρ为频率带宽;W(t)为标准Wiener过程满足(t)=ξ(t);ξ(t)为零均值和特定标准差σξ的Gauss白噪声.不同参数下中心频率Ω对输出电压均方根值Vrms的影响如图4(a)所示,其中ρ=0.2和A=0.8.内共振导致最宽的外共振频率范围,该范围覆盖了另2种两自由度系统和2种单自由度系统的外共振范围;对于变化的中心频率,除个别例外,内共振也得到最大的输出电压.当Ω=2和A=0.8时,不同参数下输出电压均方根随频率带宽的变化,如图4(b)所示.在大部分频率带宽上,内共振产生的电压最大.
3.4指数相关噪声激励

指数相关色噪声激励f(t)由Ornstein-Uhlenbeck方程定义[6].式中:γ为噪声带宽;ξ(t)为零均值和特定标准差σξ的Gauss白噪声.式(15)中白噪声ξ(t)的标准差σξ可表示色噪声强度.当γ=0.5时,不同参数下激励强度σξ对输出电压均方根Vrms的影响见图5(a).除了激励强度非常小的情形,内共振都产生最大的输出电压.给定σξ=0.2,在不同参数下,对于变化的带宽γ,内共振都给出最大的输出电压,如图5(b)所示.
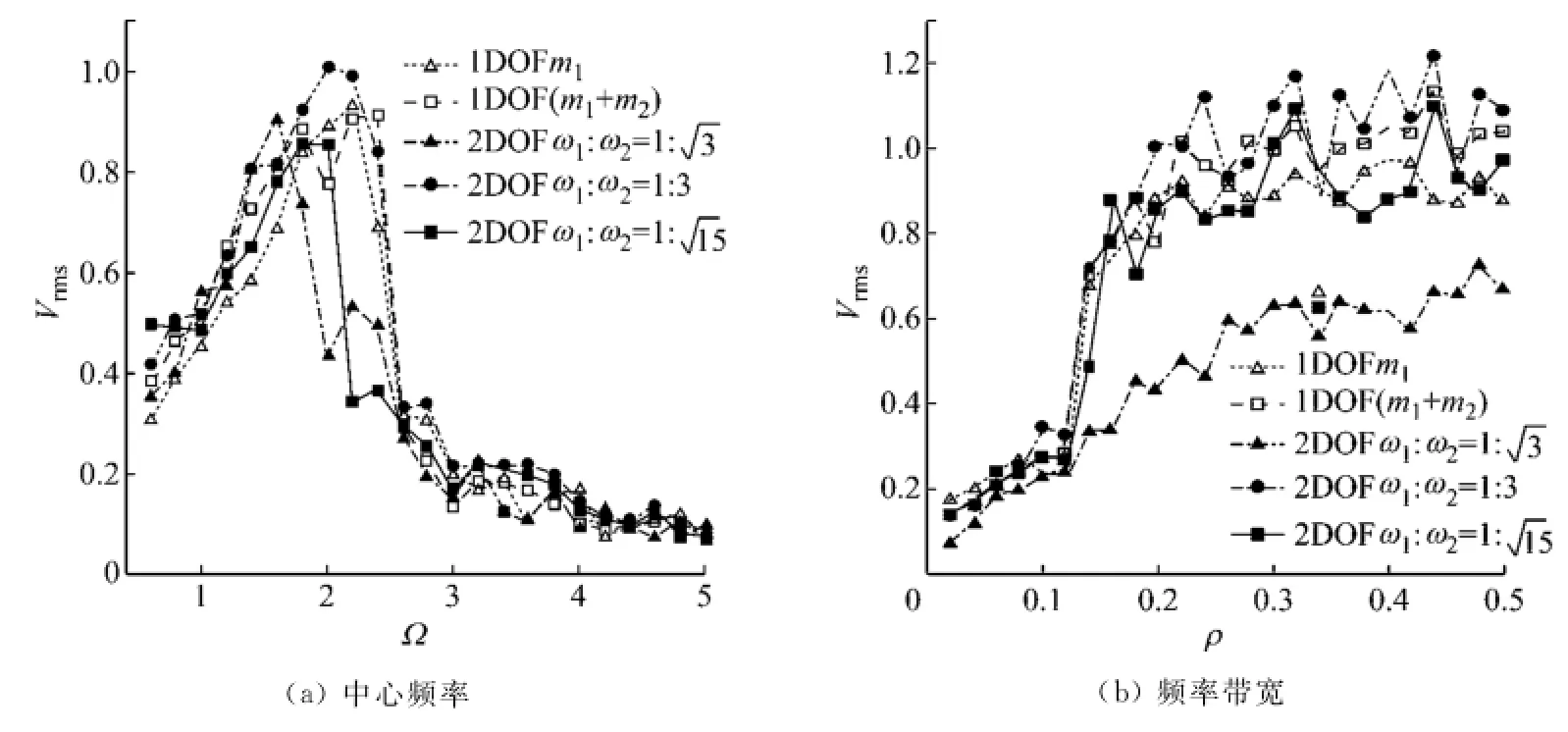
图4 不同参数下输出电压均方根随窄带色噪声(14)中心频率和频率带宽的变化Fig.4 The averaged rootmeansquare output voltage versus the center frequency and frequency bandwidth of narrowband colored noise(14)for different parameters

图5 不同参数下输出电压均方根随指数相关色噪声强度和带宽的变化Fig.5 The averaged rootmeansquare output voltage versus the intensity and bandwidth of exponentially correlated noise for different parameters
4 结 语
本文研究一类非线性压电能量采集器的设计中内共振的作用.通过忽略电量对机械系统的影响,得到了内共振条件的显式表达.数值仿真表明,在Gauss白噪声、2阶滤波给出的色噪声、窄带色噪声和指数相关色噪声4种激励下,处于内共振的能量采集器输出电压高于非内共振的情形.
[1]Priya N,Inman D J.Energy harvesting technologies [M].Berlin:Springer,2009.
[2]Erturk A,Inman D J.Piezoelectric energy harvesting [M].New Yorks:Wiley,2011.
[3]Daqaq M F,Masana R,Erturk A,et al.On the role of nonlinearities in vibratory energy harvesting:a critical review and discussion[J].Applied Mechanics Reviews,2014,66(4):040801-23.
[4]Chen L Q,Jiang W A.A piezoelectric energy harvester based on internal resonance[J].Acta Mechanica Sinica,2015,31(2):223-228.
[5]Chen L Q,Jiang W A.Internal resonance energy harvesting[J].Journal of Applied Mechanics,2015,82(3):031004-11.
[6]Daqaq M F.Transduction of a bistable inductive generator driven by white and exponentially correlated Gaussian noise[J].Journal of Sound and Vibration,2011,330(11):2554-2564.
[7]Green P L,Worden K,Atalla K,et al.The benefits of duffing-type nonlinearities and electrical optimization of a mono-stable energy harvester under white gaussian excitations[J].Journal of Sound and Vibration,2012,331(20):4504-4517.
[8]Daqaq M F.Response of uni-modal Duffing type harvesters to random forced excitations[J].Journal of Sound and Vibration,2010,329(18):3621-3631.
[9]Wedig W V.Invariant measures and lyapunov exponents for generalized parameter fluctuations[J].Structural Safety,1990,8(1-4):13-25.
(编辑吕丹)
On lnternal Resonance Piezoelectric Energy Harvesters
CHEN Liquna,b,c,JIANG Wen’anbb.S
(a.Department of Mechanics,Shang hai 2004 44,China;b.Shang hai Institute of Applied Mathematics and Mechanics;c.Shanghai Key Laboratory of Mechanics in Energy Engineering,Shanghai University,Shanghai 200072,Chin
Internal resonance can enhance piezoelectric energy harvesting. The explicit expression of internal resonance condition was derived via neglecting electric coupling.Compared with the exact vales with the account for the coupling,the errorswere small. Numerical calculations of averaged root-meansquare output voltages revealed that the piezoelectric energy harvester design via the approach performed well stimulated by the Gaussian white noise,the colored noise defined by a second-order filter,the narrow band noise,and exponentially correlated noise.
internal resonance;energy harvesting;random excitations
O 322
A
1671-7333(2015)03-0207-05
10.3969/j.issn.1671-7333.2015.03.001i
2015-04-13
国家自然科学基金重点资助项目(11232009)
陈立群(1963-),男,教授,博士生导师,主要研究方向为非线性动力学,连续体振动等.E-mail:lqchen@staff.shu.edu.cn
