网络数据流流量测量新方法

任高明,夏靖波,柏 骏,陈 珍

(空军工程大学信息与导航学院,陕西西安 710077)

网络数据流流量测量新方法

任高明,夏靖波,柏 骏,陈 珍

(空军工程大学信息与导航学院,陕西西安 710077)

针对现有的数据流流量测量概率多重计数方法空间复杂度高和空间利用率低的问题,提出了一种基于两层位域的数据流流量测量方法.该方法分为两个步骤:数据捕获阶段.将到达数据包采用两个独立的哈希函数分别映射至两层位域;数据恢复阶段.对位域恢复得到的两个虚拟矩阵按位取交集,消除哈希碰撞引起的误差.实验结果表明,和概率多重计数方法相比,两层位域方法在存储空间降低75%的前提下,仍具有高的数据流估算精度.

计算机网络;流量测量;数据流估算;位域

网络流量测量对流量计费、流量工程与异常检测等网络运营管理具有重要意义[1].随着以太网技术的迅速发展和40 GB/100 GB标准的发布,基础网络快速进入超高速时代.随着网络链路速率的增长,数据包到达频率越来越高,单位数据包的处理时间越来越短,测量每个数据包的信息变得越发困难[2-3].根据吉尔德定律,主干网的带宽每6个月增长1倍,其增长速度是莫尔定律预测的CPU增长速度的3倍.也就是说,用于网络测量的硬件性能和网络带宽之间的差距会越来越大,网络流量测量任务将越来越艰巨[4].

在网络流量测量初期,通用的方法是全数据测量,该方法测量准确.然而网络链路速率的提高暴露了该方法的缺点,即处理速度慢、产生数据量大和所需存储空间大等[5].网络流量抽样技术的应用很好地解决了全数据测量方法的缺点[6],大幅提高了网络流量测量设备的处理效率,同时,又能保证准确性在可接受的错误范围内[7].抽样方法很快得到普及应用,例如当前广泛使用的思科推出的网络设备Net Flow就采用了抽样技术[8].但是,数据包抽样技术由于测量不准确,随着链路速率的提高已难以满足需要[9-10].近年来,基于概率的网络流量测量机制方法以流(通常流的定义为,在测量时间内五元组相同的数据包组成的集合)为单位,其可满足当前网络线速处理要求,并能较为准确地估算出所有流的大小[11],受到越来越多的关注.

1 相关工作

在当前的高速网络中,准确测量每个流的大小非常困难,并且代价昂贵.根本原因是,网络带宽的增加,使得数据包到达频率越来越高,每个数据包的处理间隙越来越短.以40 Gbit/s链路为例,数据包处理间隙只有12 ns,也就是说,测量设备必须在12 ns内完成1个数据包的处理,因此,直接进行数据流流量的准确测量代价极高.目前,网络流量测量方法的时间复杂度通常以哈希映射和内存访问的次数来衡量,哈希映射和内存访问的次数越少,时间复杂度就越低.近年来,基于概率理论的数据流流量测量方法受到越来越多的关注.文献[12]提出一种新的计数器结构分层计数器(Counter Braids,CB),通过随机图编织分层的计数器和计数器共享,能较好地完成数据流流量的估算,但该方法时间复杂度高,处理每个数据包至少需要3次哈希映射和6次内存访问.文献[13]采用多个具有不同解析度的空间编码布鲁姆过滤器(Space-Code Bloom Filter, SCBF),每个SCBF对某一段值(流大小)有较高的精度.因此,对于一个任意大小的流,都有一个适合的SCBF,使得对它的估算达到一定的准确性.但上述两种方法都存在相同的缺点,即较高的时间复杂度限制了其扩展性.

文献[14]在FM sketches方法[15]的基础上提出概率多重计数(the Probability of Multiple Counting, PMC)网络数据流流量测量方法.该方法由流量捕获和流信息提取两个步骤组成,分别在实时测量阶段和后台分析时完成.其中,每个流对应一个虚拟矩阵,实现过程以流f为例说明.当属于流f的数据包p到达时,分别采用函数rand(m)和georand(w)确定p在对应虚拟矩阵VMf中的行和列.函数rand(m)生成范围是在[1,m]之间的均匀分布的随机整数;函数georand(w)生成服从几何分布的随机数,满足以下关系:

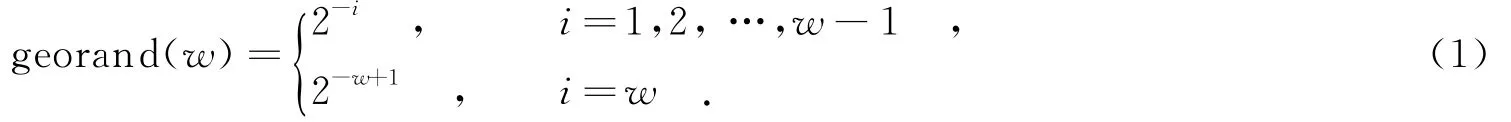
之后,p经哈希函数H(f,i,j)(f为流关键字,i和j分别为数据包在所属流对应的虚拟矩阵中的位置编号)映射至一个长度为L的位域(bit field)B中,并将B[H(f,i,j)]位赋值为1;在测量周期结束后,根据位域中存储的信息估算出每个流的大小.和其他方法相比,PMC方法的最大优势在于,将测量过程分为线上采集和线下恢复两个阶段,只需在线上采集时满足测量设备限速处理的要求即可,而对线下恢复阶段的效率不进行实质性的要求.同时,PMC利用位域存储特点,在采集时处理每个数据包只需1次哈希映射和1次内存访问,避免了根据流关键字信息去查找流所属的存储单元这一最消耗资源的操作,其处理速度足够快,可满足高速网络流量测量的线速处理需求.PMC方法的具体内容请参考文献[14],在此不再赘述.

然而PMC方法的不足之处在于,其估算误差由位域B的填充率惟一决定,对于同一组实验数据,位域长度越大,B的填充率越小,存储资源消耗越大,PMC方法的准确率越高.但在实际应用中,大量的存储资源意味着高昂的代价,因此,必须在准确性和实现代价之间做出合理的折中.为保持准确性,文献[14]提到,在一般情况下,PMC方法中位域的长度设置为几百万时是较合理的.但此时,算法的空间复杂度较高,且空间利用率低,极大限制了测量方法的灵活部署.基于此,找到一种所需存储空间小、单个数据包处理时间短,同时具有很高准确性的方法,成为当前流量测量工程应用中亟待解决的问题.

2 两层位域法

文中在保留PMC方法优势的基础上,提出一种新的网络数据流流量测量方法,在大幅降低所需存储空间的同时,仍保证更高的准确率.

PMC方法所需存储空间的大小由位域的长度L决定,减小存储空间的惟一方法就是缩短L.对相同的流量数据,L的缩短必然会增大哈希碰撞发生的概率,进而导致准确率的降低.在保证准确率的前提下,降低空间复杂度,似乎是不可能完成的任务.下面分析缩短PMC方法中位域长度L后导致测量误差变大的原因.

在测量时间段内,当流f包含的数据包全部到达后,对应的虚拟矩阵VMf将确定.假定位域L的长度无限大,哈希函数的散列性足够好,那么,虚拟矩阵VMf经哈希函数H(f,i,j)映射后,会将位域B中两两不同的位赋值为1,不会出现虚拟矩阵中不同的位置被映射至位域中相同位的情况.类似地,不同流对应的虚拟矩阵在被哈希函数映射后,相互之间也不会发生哈希碰撞.因此,在流信息提取阶段,对于流f,从位域恢复得到的虚拟矩阵V′Mf将和VMf相同.但在现实条件下,基于成本优化和实际硬件水平的考量,并不能满足理想条件,尤其在存储空间大幅减小的情况下,必然会引起大量的哈希碰撞,导致恢复得到的虚拟矩阵V′Mf和流f的虚拟矩阵VMf之间存在较大的误差.

假定虚拟矩阵VMf中(i,j)位为0,经哈希函数H(f,i,j)映射后,位域B中B[H(f,i,j)]位的值仍为0;那么,从位域中恢复虚拟矩阵VMf时,(i,j)位为0.类似地,若虚拟矩阵VMf中(i,j)位为1,经过存储至位域B后,再恢复虚拟矩阵时,仍然会得到V′Mf中的(i,j)位为1,并不会误判为0,即不会出现假阴性误判.而由于哈希碰撞的存在,可能会出现下面的情况:属于不同流的两个数据包映射至同一位,如H(f1,i,j)=H(f2, i′,j′),由于流f2的虚拟矩阵中(i′,j′)为1,导致恢复时,将流f1的虚拟矩阵中原本为0的(i,j)位确定为1,从而出现假阳性误判.

在此背景下,文中提出一种基于两层位域的数据流估算方法(D-BF),其基本出发点是通过减少恢复虚拟矩阵时的假阳性误判,保证在减小存储空间的同时,仍具有较高的准确率.该方法由两层长度为L′(L′＜1/(2L))的位域组成,基本思想如图1所示,包括网络流量的实时捕获和流信息提取两部分.

图1 D-BF方法结构

在流量捕获阶段,当属于流f的数据包p到达时,根据函数ran d(m)和georan d(w)确定到达的数据包在虚拟矩阵VMf中的位置(i,j)后,采用并行的哈希函数H1和H2将数据包分别映射至位域B1和B2中的B1(H1(f,i,j))和B2(H2(f,i,j))位,赋值为1,并保存.图2为流a和流b映射到位域B1和B2的示意图.

在流信息提取阶段,首先,对于给定的流f,将数据包关键字和虚拟矩阵的行与列分别组合,即根据不同的(f,i,j)组合(其中,i=1,2,3,…;j=1,2,3,…),分别使用哈希函数H1和H2,从位域B1和B2得到VM1和VM2;然后,对二者按位取交集得到虚拟矩阵VMinter,具体实现过程如算法1所示.

算法1 GET VMinter(f)

VM1=0,VM2=0,VMinter=0

for i=1…m do

for j=1…w do

if B1[H1(f,i,j)]=1 then VM1(i,j)←1

if B2[H2(f,i,j)]=1 then VM2(i,j)←1

if(VM1(i,j)==1)&&(VM2(i,j)==1)

then VMinter(i,j)←1

end for

end for

return VMinter(f)

对虚拟矩阵VM1和VM2取交集时,相同的位置同为1,则将虚拟矩阵VMinter中相同的位置为1;否则,置为0.

文中提出使用两层并行位域记录流信息,对从两层位域恢复得到的虚拟矩阵VM1和VM2按位取交集得到VMinter,其某一位置出现假阳性误判的前提条件是,VM1和VM2中相同的位置均出现假阳性误判.因此,误判概率大大降低,进而减小了虚拟矩阵VMinter和VM之间的误差.得到虚拟矩阵VMinter后,借鉴PMC方法计算出k和Z,估算出流大小.具体如下:在虚拟矩阵中,如果k/(1-p)＞0.3m,则可以估算出流f的大小(文中流的大小指流所包含的数据包个数),n=-2m log(k(m(1-p))),其中,k为虚拟矩阵中第1列中0的个数;否则,n=2Z/mm/φ(p),其中,Z为每一行初始的、连续的1的个数之和;φ的值取决于n,Flajolet和Martin证明,当n→∞时,φ=0.773 51.φ值收敛得非常快,在使用时,可认为是常量.具体计算Z的方法如算法2所示.

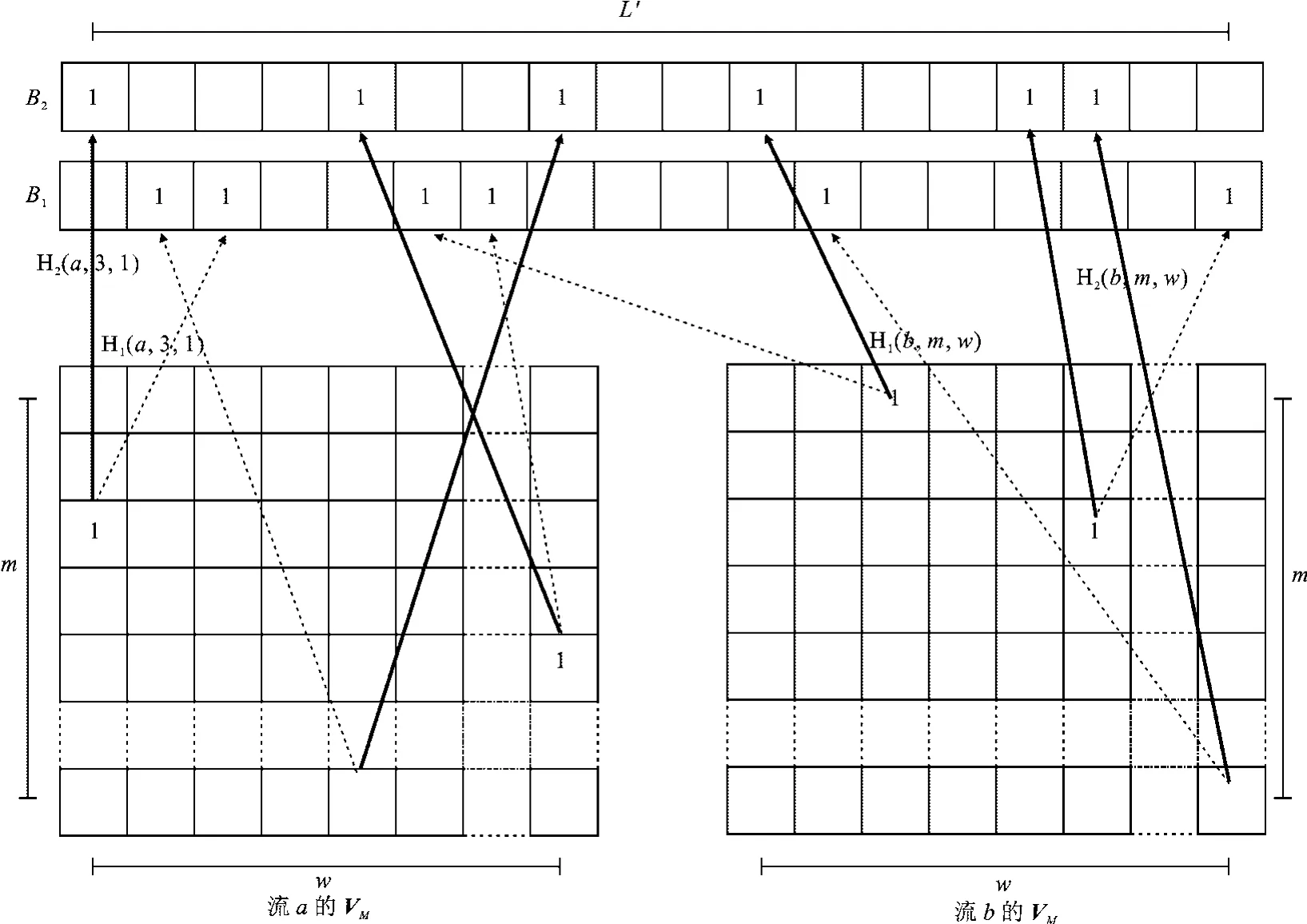
图2 D-BF方法映射示意图

算法2 GET ZSUM(f)

Z←0

for i=1…m do

For j=1…w do

if B[H(f,i,1)]=0 then break

end for

Z←Z+(j-1)

end for

return Z

3 理论分析

3.1 准确性分析

虚拟矩阵VM的维数为w×m,假定用于确定位置的函数rand(m)和georand(m)随机性足够好,不会出现碰撞,流f包含n个数据包.根据函数georand(m)易知,有数据包到达时,定位在前5列的概率可近似认为流f的数据包到达时,会全部落在前5列.假定位域B的长度为L,填充率为p.

(1)如果0.97n≥5m,则可近似为n≥5m,即B中5m个位置被置1,剩余(w-5)m个位置为0.在从位域B恢复的时候,每个位置被错误地置为1的概率为(Lp-5m)(L-5m),由于在实际测量过程中数据量巨大,可近似表示为p剩余(w-5)m个位置被错误地置为1的概率为

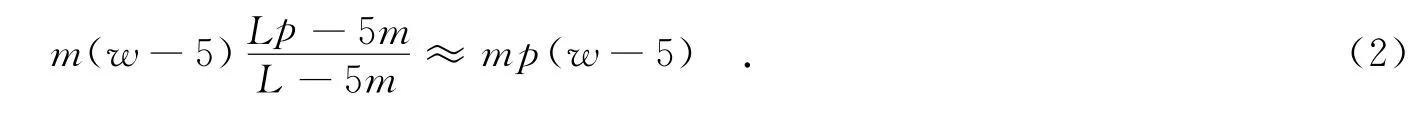
(2)如果0.97n≤5m,则可近似为n＜5m.在从位域B恢复时,每个位置被错误地置为1的概率为(Lp -n)(L-n),近似为p,类似地,剩余wm-n个位置被错误置为1的概率为

和PMC方法相比,D-BF方法减小存储空间后,位域长度由L减小为L′,对于同样的实验数据,位域的填充率将变大,假定在D-BF方法中,位域B1和B2的填充率均变为p′,易知p′=LpL′.D-BF方法在数据恢复时,发生错误的条件是VM1和VM2中同一个位置均被错误地置为1.可知,D-BF方法在从位域B1和B2恢复时,每个位置被错误地置1的 概率为((L′p′-5m)(L′-5m))2或者((L′p′-n)(L′-n))2,可近似表示为(p′)2.和PMC方法相比,保证D-BF方法准确性不会降低的条件是(p′)2＜p,结合式(3),可得到

同时,要保证D-BF方法的存储空间小于PMC方法的,需满足2L′＜L,易得出

只要L′满足上述条件,和PMC方法相比,D-BF方法在降低存储空间的同时,将会提高准确性.

3.2 时间复杂度分析

与前述一致,这里使用操作次数作为衡量方法时间复杂度的性能指标.由于恢复阶段的处理效率不会影响方法应对高速网络的执行效率,故借鉴文献[14]的分析方法,只考虑线上采集时的时间复杂度.表1列出了D-BF方法和PMC方法在处理每一个数据包所需要的操作次数.可以发现,D-BF方法处理每个数据包需要产生随机数两次、哈希映射两次和写操作两次.但由于两层位域的并行性,在实际应用时,可采用并行处理方法,同时处理两层位域的存储操作,这样并不会降低D-BF方法的处理效率,而且是切实可行的.

3.3 空间复杂度分析

和PMC方法类似,D-BF方法所需的存储空间同样取决于位域大小.PMC方法采用一层位域B,其所需空间为L bit.D-BF方法使用两层位域B1和B2,长度相同,均为L′bit,共需2L′bit.由于L′p′=Lp,可知D-BF方法需要的存储空间为2Lpp′.即D-BF方法与PMC方法所需存储空间的比值2L′L=2pp′.

为方便表示,定义位域B的长度L=RN,其中,N为实验所用的数据包个数,R为系数.假定PMC方法中采用的哈希函数效果良好,不会发生哈希碰撞,那么实验使用N个数据包,位域B中将会有N被置1,那么,位域B的填充率p=1R,与D-BF方法类似.表2为L′、L、p和p′取几种典型值时,D-BF方法和PMC方法所需空间之比.

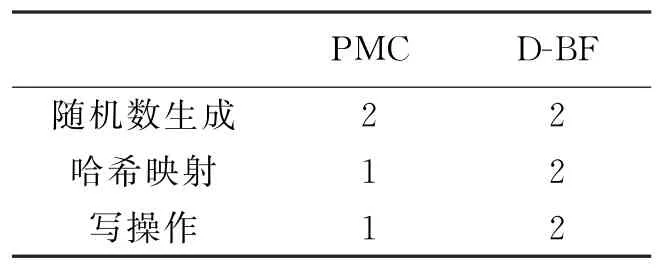
表1 两种方法的操作次数比较

表2 D-BF方法和PMC方法所需空间之比

4 仿真实验

选用文献[14]中的PMC方法作为参照,两种算法在相同的存储空间下的测量数据流流量的准确性进行比较.所用仿真环境如下:仿真工具为MATLAB R2010a;计算机CPU为Pentium(R)Dual-Core,主频为2.69 GHz;内存为3 GB;操作系统为Windows XP SP3.实验数据来自CAIDA提供的某2.5 GB链路的真实互联网流量.由于计算机性能受限,选择流量数据的前10万个数据包作为实验对象.

为保证实验的公平性,参照文献[14],m和w值分别取32和256.当m和w确定后,R系数的值决定了位域的长度,即所需空间的大小.

图3为PMC方法在不同R值条件下的估计误差示意图.可以看出,随着R系数的增大,PCM方法的误差在不断变小,原因是φ=0.77是在假定填充率1/R无限趋近于零时计算得到的.因此,R越大,位域B的填充率1/R越接近于零,更接近于假设条件,估计值越准确,误差越小;当R＞800时,误差变化幅度不大,原因是当位域B的填充率1/R非常趋近于零时,继续减小将不会明显降低测量误差.

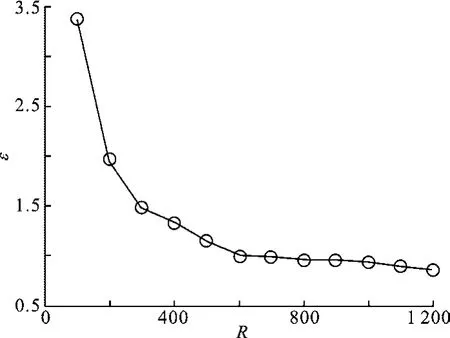
图3 PMC方法误差变化图

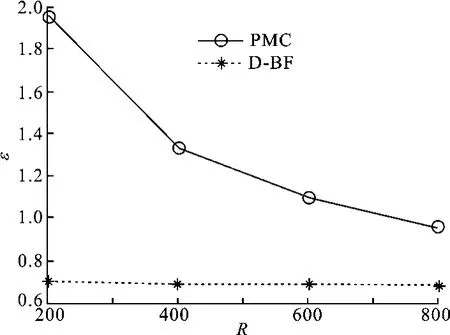
图4 PMC方法和D-BF方法误差比较图

图4为R系数的取值在[200,800]区间时,PMC方法和D-BF方法的误差比较图.给定PMC方法的存储空间L=RN bit,为保证两种方法存储空间相同,设定D-BF方法中两层位域的长度均为L′=RN2 bit.由图4可以发现,在[200,800]区间内,D-BF方法随着R系数的增大,测量误差基本恒定,并且均小于PMC方法的估计误差.

图5 PMC方法和D-BF方法实验效果图

图5为两种方法的R系数分别取200和800时,数据流流量的测量图.图5中的每个点代表1个流,x轴的值表示该流包含数据包的实际个数,y轴的值表示估算得到的数据包个数.理想状况下,测量完全准确时,图5中所有的点都应该在y=x的直线上.图5(a)和图5(b)分别表示R=200时,PMC方法和D-BF方法的数据流流量的测量图.可以发现,在相同的存储空间条件下,D-BF方法测量图中的点明显靠近于y=x直线;比较图5(c)和图5(d)可以得到相同结论.比较图5(a)和图5(c)、图5(b)和图5(d)可以发现,PMC方法取R=800时的准确率高于R=200时的准确率;而D-BF方法在R=200和R=800时,得到的效果图区别并不明显.

比较图5(b)和图5(c)可见,D-BF方法在R=200时的准确率明显高于PMC方法在R=800时的准确率,也就是说,和PMC方法相比,D-BF方法在存储空间降低75%的情况下,准确性仍优于PMC方法,这和图4分析得到的结论一致.

5 结束语

随着网络链路速率的不断增长,用于网络流量测量的硬件技术已无法满足需要.静态随机存储器速度足够快,但空间小、体积大、价格高;动态随机存储器能够提供足够的存储空间,但访问速度慢,无法满足当前线速处理的要求.因此,设计一种空间利用率高、计算速度快、误差小的网络流估算方法意义重大.

笔者提出一种基于两层位域的网络流估算(D-BF)方法,与已有的PMC方法相比,D-BF方法所需存储空间少,准确率高.采用实际网络采集的流量数据试验后发现,D-BF方法在存储空间节省75%的前提下,仍具有更高的准确性.尽管D-BF方法处理每个数据包需要的操作次数多于PMC方法的,但在实际应用时,可以采用并行处理方法同时处理两层位域的存储操作,并不会降低D-BF方法的处理效率.D-BF方法空间复杂度的大幅降低,使得其更适合于网络流量测量设备的工程应用,在只需要较小的SRAM的条件下,完成准确性较高的流量测量,增加了部署的灵活性.

[1]Huici F,Di Pietro A,Trammell B,et al.Blockmon:a High-performance Composable Network Traffic Measurement System[J].Computer Communication Review,2012,42(4):79-80.

[2]Kodialam M S,Lakshman T V.High-speed Traffic Measurement and Analysis Methodologies and Protocols:U.S. Patent 7,808,923[P].2010-10-05.

[3]孙昱,蒋馥蔚,夏靖波,等.一种改进的高速网络分布式流量抽样算法[J].西安电子科技大学学报,2013,40(3):160-165. Sun Yu,Jiang Fuwei,Xia Jingbo,et al.Improved Distributed Traffic Sampling Algorithm for High Speed Network[J]. Journal of Xidian University,2013,40(3):160-165.

[4]Aghdai A,Zhang F,Dasanayake N,et al.Traffic Measurement and Analysis in an Organic Enterprise Data Center[C]// Proceedings of IEEE 14th International Conference on High Performance Switching and Routing.Piscataway:IEEE Computer Society,2013:49-55.

[5]张震,汪斌强,张风雨,等.基于LRU-BF策略的网络流量测量算法[J].通信学报,2013,34(1):111-120. Zhang Zhen,Wang Binqiang,Zhang Fengyu,et al.Traffic Measurement Algorithm Based on Least Recent Used Bloom Filter[J].Journal on Communications,2013,34(1):111-120.

[6]周爱平,程光,郭晓军.高速网络流量测量方法[J].软件学报,2014,25(1):135-153. Zhou Aiping,Cheng Guang,Guo Xiaojun.High-speed Network Traffic Measurement Method[J].Journal of Software, 2014,25(1):135-153.

[7]Estan C,Varghese G.New Directions in Traffic Measurement and Accounting[J].Computer Communication Review, 2002,32(4):323-336.

[8]De Godoy S,Jeferson W,Ling L L.A New Binomial Conservative Multiplicative Cascade Approach for Network Traffic Modeling[C]//IEEE 27th International Conference on Advanced Information Networking and Applications.Piscataway: IEEE,2013:794-801.

[9]Gebert S,Pries R,Schlosser D,et al.Internet Access Traffic Measurement and Analysis[C]//Lecture Notes in Computer Science:7189.Berlin:Springer,2012:29-42.

[10]Chang C W,Liu H,Huang G,et al.Distributed Measurement-aware Routing:Striking a Balance between Measurementand Traffic Engineering[C]//Proceedings of IEEE Conference on Computer Communications.Piscataway:IEEE,2012: 2516-2520.

[11]Marold A,Lieven P,Scheuermann B.Probabilistic Parallel Measurement of Network Traffic at Multiple Locations[J]. IEEE Network,2012,26(1):6-12.

[12]Lu Y,Montanari A,Prabhakar B,et al.Counter Braids:a Novel Counter Architecture for Per-flow Measurement[J]. Performance Evaluation Review,2008,36(1):121-132.

[13]Kumar A,Xu J,Wang J.Space-code Bloom Filter for Efficient Per-flow Traffic Measurement[J].IEEE Journal on Selected Areas in Communications,2006,24(12):2327-2339.

[14]Lieven P,Scheuermann B.High-speed Per-flow Traffic Measurement with Probabilistic Multiplicity Counting[C]// Proceedings of IEEE Conference on Computer Communications.Piscataway:IEEE,2010:1-9.

[15]Flajolet P,Nigel Martin G.Probabilistic Counting Algorithms for Data Base Applications[J].Journal of Computer and System Sciences,1985,31(2):182-209.

(编辑:齐淑娟)

Novel per-flow traffic measurement algorithm

REN Gaoming,XIA Jingbo,BAI Jun,CHEN Zhen
(School of Information and Navigation,Air Force Engineering University,Xi’an 710077,China)

It is extremely difficult to measure traffic information with a growing network link speed.In recent years,increasing focus has been put on probabilistic algorithms which are fast enough to examine all packets and can provide estimates of the sizes of all flows.However,the previously proposed flow estimating algorithm of PMC has the drawbacks of poor space efficiency and large estimation error.To address the problem,a double bit field(D-BF)algorithm is proposed.The method is divided into two steps:the newly arrived packet is mapped to two bit fields using different hash functions in the data capturing stage;two virtual matrixes recovered from the bit fields have been intersected to eliminate errors caused by the hash collision in the data recovering stage.Experimental results show that the proposed D-BF is more accurate than PMC in flow estimate,while a reduction of 75%in memory space can be achieved.

computer network;traffic measurement;flow estimate;bit field

TP393

A

1001-2400(2015)05-0125-08

2014-05-07< class="emphasis_bold">网络出版时间:

时间:2014-12-23

国家自然科学基金资助项目(61202489);陕西省自然科学基础研究计划资助项目(2012JZ8005)

任高明(1986-),男,空军工程大学博士研究生,E-mail:gaomingr_928@126.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20141223.0946.022.html

10.3969/j.issn.1001-2400.2015.05.022