线性模式开关电容变换器的混沌控制

李先锐,朱彦丽,申 瑞,刘 茜

(1.西安电子科技大学电路CAD研究所,陕西西安 710071; 2.西安电子科技大学超高速电路设计与电磁兼容教育部重点实验室,陕西西安 710071)

线性模式开关电容变换器的混沌控制

李先锐1,2,朱彦丽1,2,申 瑞1,2,刘 茜1,2

(1.西安电子科技大学电路CAD研究所,陕西西安 710071; 2.西安电子科技大学超高速电路设计与电磁兼容教育部重点实验室,陕西西安 710071)

以反馈系数K为参数,研究线性模式开关电容DC-DC变换器的非线性行为并得到分岔图.当反馈系数比较大时,系统出现混沌现象.基于减小反馈系数、提高稳定性的思想,提出了在基准电压输入端添加基准电压调整模块的拓扑结构,增加的基准电压调整模块由两级运放组成.分析了增加基准电压调整模块前后变换器的反馈系数,并对其进行了仿真,得到了输出电压的时域波形和相图.仿真的结果表明,所加入的基准电压调整模块能有效地抑制混沌现象,改善系统的稳定性.

线性模式;开关电容DC-DC;混沌控制

DC-DC变换器含有开关元件,是一种强非线性系统.在一定的反馈条件下,DC-DC变换器会呈现丰富的非线性动力学行为,处于混沌状态[1-3].虽然可利用混沌序列良好的相关性和随机性以及混沌吸引子的稳定性和分形性优化系统性能,或利用混沌状态具有无穷多不稳定周期轨道来改善变换器中的电磁兼容性等,但一般来说,变换器处于混沌状态时,其性能恶化,难以预测,电压转换效率低[4-8]等.对变换器的混沌行为进行控制,是一个重要的研究课题.文献[9-10]中采用状态变量延迟反馈控制方式抑制DC-DC变换器的混沌现象;文献[11]应用自适应斜坡补偿控制策略抑制了DC-DC变换器的混沌现象.以上研究只是针对电感型DC-DC变换器,对于如何抑制开关电容DC-DC变换器的混沌现象,报道较少.

针对现有线性开关电容DC-DC变换器出现混沌现象的问题,笔者提出了一种抑制线性开关电容DC-DC变换器混沌现象的基准电压调整电路,对处于混沌状态的变换器施以控制,达到要求的稳定周期状态.

1 线性模式开关电容DC-DC

图1显示了线性模式开关电容DC-DC的电路图.阶段A为充电阶段,S1导通,S2关闭,电容C1被Vin充电;阶段B为能量传输阶段,S2导通,S1关闭,电容C1向输出电容C2放电.在电源电压或负载电流变化时,反馈环路通过控制运放来调节RC的值,从而稳定输出电压.

图1 线性模式开关电容DC-DC变换器电路图

设v1、v2分别为电容C1、C2上的电压,r为电容C1的等效串联电阻,S1、S2为理想开关(即导通电阻为零),D为CLK的占空比.可以得到线性模式控制开关电容DC-DC变换器的二维离散映射模型方程.将v1、v2作为状态变量的映射方程,分别写为

2 线性模式开关电容DC-DC变换器的分岔图

图1中的参数设置如下:Vin=6 V,VREF=3 V,C1=4.7μF,C2=4.7μF,RL=20Ω,T=1μs,r=0.1Ω, D=0.257 1,R=5Ω.

以反馈系数K为参数,用MATLAB对映射方程式(1)进行迭代计算.取K的步长为1,并去掉与初值有关的前300个迭代值,得到电压v2随K变化的分岔图,如图2所示.

由图2可以看出,当K大约为699时,系统出现倍周期分岔;当K大约为860时,系统出现4周期分岔;当K约为910时,系统进入混沌状态.

图2 电压v2随反馈参数K变化的分岔图

3 混沌控制的方法

在图1中,RC的值随着放大器(AMP)输出的变化而变化.设比例系数为l,放大器的输出为VAMP,则RC的值可以写为

RC的变化可以写为

VAMP和VREF的关系为

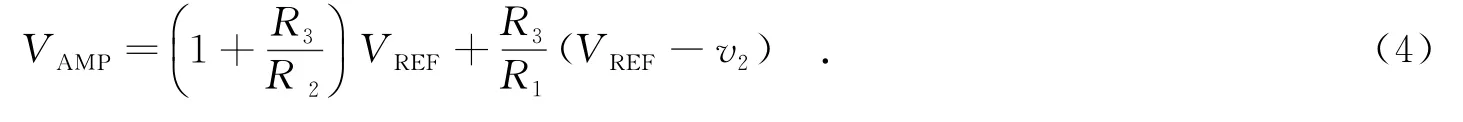
VAMP的变化可以写为

由式(3)和式(5)可得

根据RC=R-K[v2(n)-VREF],可得

由式(6)和式(7)可得

由图2可知,混沌现象与K的值有关.在相同的条件下,只要减小K的值就可以有效地抑制混沌现象.所以,可以使K的表达式变为

其中m、n为比例系数.只要调整m、n的值,就可以改变K的值,使它在稳定的范围内.

笔者在线性模式开关电容DC-DC变换器中设计了基准电压调整电路,改变K值实现了混沌控制.图3 (a)为添加了基准电压调整模块的原理图,图3(b)为基准电压调整模块的电路图.

图3 新的线性模式开关电容DC-DC变换器电路

基准电压调整电路中包括两个差分比例运算电路,差分比例运算电路1的输入电压为v2和VREF,输出电压v3的值为(R4=R6,R5=R7)

差分比例运算电路2的输入电压为v3和VREF,输出电压VREF1的值为(R8=R9=R10=R11)

VREF1的变化可以写为

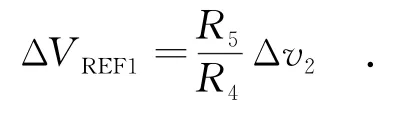
设放大器的输出为VAMP1,则VAMP1可以写为

假设R3≫R1,VAMP1的变化为

假设反馈参数为K1,根据式(3)和式(7),可得

在相同的条件下,可以调整R5和R4的值来改变K1的值,使它处在稳定工作的范围内.

4 仿 真

下面用Pspice软件仿真相同条件下图1和图3所示的电路.

电路的参数设置如下:Vin=6 V,VREF=3 V,C1=4.7μF,C2=4.7μF,RL=20Ω,T=1μs,r=0.1Ω,D=0.257 1,R2=9.9 kΩ,R3=100Ω,R1=0.1Ω,R8=R9=R10=R11=1 kΩ,R4=R6=10 kΩ,R5= R7=6.65 kΩ.仿真的时域波形和相图分别如图4和图5所示.

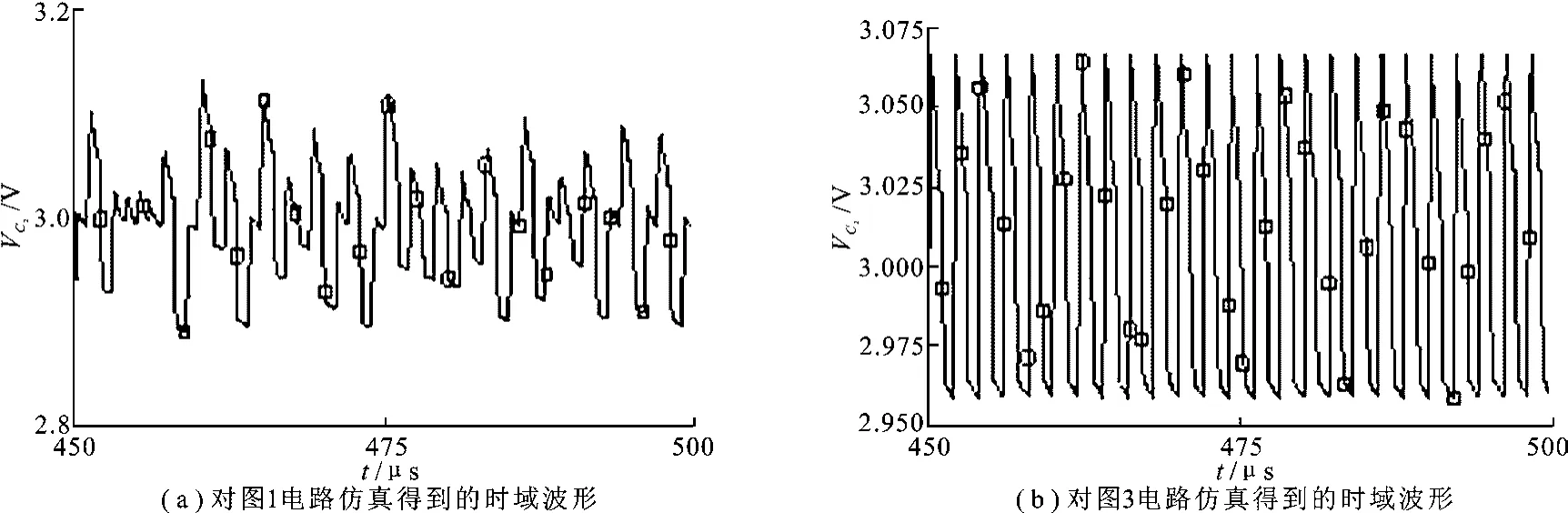
图4 有无混沌控制模块电路仿真时域对比图

图5 有无混沌控制模块电路的相图

由图4和图5可以看出,在相同条件下,加入基准电压调整模块能有效地抑制混沌现象.

改变R5的值,可以控制电路在倍周期和四周期状态下工作.倍周期的仿真图如图6所示,四周期的仿真图如图7所示.

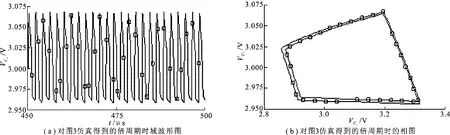
图6 对图3仿真得到的倍周期时域及相图

5 结束语

通过对线性模式开关电容DC-DC变换器的拓扑结构的研究,得到了分岔图,并在反馈参数比较大的时候,系统出现混沌现象.在减小反馈参数的思想下,笔者在线性模式开关电容DC-DC变换器的拓扑结构中添加了基准电压调整模块.在相同条件下,对增加和没有增加基准电压调整模块的变换器进行了仿真,仿真结果表明,所加入的基准电压调整模块能有效地抑制混沌现象,提高系统的稳定性.

图7 对图3仿真得到的四周期时的时域及相图

[1]来新泉,何惠森,许文丹,等.一种精简的高速率功率MOS驱动器[J].西安电子科技大学学报,2012,39(2):168-174. Lai Xinquan,He Huisen,Xu Wendan,et al.High-speed Gate Driver with a Simple Structure for Power MOSFET[J]. Journal of Xidian University,2012,39(2):168-174.

[2]李先锐,来新泉,王松林,等.高精度可编程恒流驱动白光LED芯片设计研究[J].西安电子科技大学学报,2009,36 (3):433-437. Li Xianrui,Lai Xinquan,Wang Songlin,et al.Design Research on the High-precision Programming Constant Current Driver of the White Light LED[J].Journal of Xidian University,2009,36(3):433-437.

[3]Deivasundari P,Uma G,Ashita S.Chaotic Dynamics of a Zero Average Dynamics Controlled DC-DC Cuk Converter[J]. IET Power Electrons,2014,7(2):289-298.

[4]Jiang X W,Ding L.Bifurcation and Chaotic Behavior of a Discrete-time Ricardo-Malthus Model[J].Nonlinear Dynamics,2013,71(3):437-446.

[5]张立森,王立志.PWM型开关电容DC-DC变换器的非线性动力学行为研究[J].电子学报,2008,36(2):266-270. Zhang Lisen,Wang Lizhi.Study on Nonlinear Dynamics Behavior in PWM Switched-Capacitor DC-DC Converter[J]. Acta Electronica Sinica,2008,36(2):266-270.

[6]Angulo F,Ocampo C,Olivar G.Rafael Ramos Nonlinear and Non-smooth Dynamics in a DC-DC Buck Converter:Two Experimental Set-ups[J].Nonlinear Dynamics,2006,46(3):239-257.

[7]姜建国,刘永青,尚海豹,等.一种改进的类电磁机制算法[J].西安电子科技大学学报,2013,40(3):87-94. Jiang Jianguo,Liu Yongqing,Shang Haibao,et al.Improved Electromagnetism-like Mechanism Algorithm[J].Journal of Xidian University,2013,40(3):87-94.

[8]金爱娟,邢军,赵东方,等.Buck变换器频率引起的混沌及其控制[J].控制工程,2014,1(61):66-73. Jin Aijuan,Xing Jun,Zhao Dongfang,et al.Chaos and Chaotic Control Varied with Frequency in Buck Converter[J]. Control Engineering of China,2014,1(61):66-73.

[9]Li H,Li Z,Zhang B,et al.The Stability of a Chaotic PWM Boost Converter[J].International Journal of Circuit Theory and Applications,2011,39(5):451-460.

[10]Feki M.Optimizing the Dynamics of a Two-cell DC-DC Buck Converter by Time Delayed Feedback Control[J]. Communications in Nonlinear Science and Numerical Simulation,2011,16(11):4349-4364.

[11]来新泉,李祖贺.基于自适应斜坡补偿的双环电流模DC-DC混沌控制[J].物理学报,2010,59(4):2256-2264. Lai Xinquan,Li Zuhe.Control of Chaos Indouble-loop Current-mode DC/DC Based on Adaptive Slope Compensation[J]. Acta Physica Sinica,2010,59(4):2256-2264.

(编辑:郭 华)

Control of chaos of the linear-mode switched-capacitor converter

LI Xianrui1,2,ZHU Yanli1,2,SHEN Rui1,2,LIU Qian1,2
(1.Research Inst.of Electronic CAD,Xidian Univ.,Xi’an 710071,China;2.Ministry of Education Key Lab.of High-Speed Circuit Design and EMC,Xidian Univ.,Xi’an 710071,China)

This paper studies the bifurcation and non-linear dynamic behaviors of the linear-mode switchedcapacitor DC-DC converter with the parameter K and the fact that the system appears chaotic when the feedback coefficient is relatively large.In this paper we propose converter topology by increasing a reference voltage regulator module in the reference voltage input,which improves the system stability.The reference voltage regulator module consists of the two stage amplifier.In this study,the feedback coefficients of the converter with and without the reference voltage regulator module are analyzed,respectively.The output voltage of the timedomain waveform and phase diagram are obtained through the simulation Simulation shows that the reference voltage regulator module added can effectively suppress the chaos and improve the system stability.

linear-mode;switched-capacitor DC-DC;chaos control

TN431.1

A

1001-2400(2015)05-0110-05

2014-04-29< class="emphasis_bold">网络出版时间:

时间:2014-12-23

国家自然科学基金资助项目(F040202);中央高校基本科研业务费专项资金资助项目(JB140210)

李先锐(1974-),女,副教授,博士,E-mail:lixr@xidian.edu.cn.

http://www.cnki.net/kcms/detail/61.1076.TN.20141223.0946.019.html

10.3969/j.issn.1001-2400.2015.05.019