平板式感应加热线圈磁场的分布特性

薛萍++孙浩++李雪娇++王宇

摘要：平板式感应加热加热死区的存在，使其不能广泛应用于工业领域.为了研究它的工业应用的潜力，文中对感应加热的核心部件——线圈进行了深入研究.依据经典电磁场理论，研究了线圈的磁场分布特性，先对圆环电流进行研究，计算它的磁场分布，进而对饼式线圈的磁场分布特型进行有限元计算，并与实验采集数据对比后，总结出饼式线圈的磁场分布特性，此特性表明，采用饼式线圈的平板感应加热，板上必然会出现加热死区.因此加热均衡性的实现需要对整个装置进行全方位的改进，以上结论可为平板式感应加热的后续研究提供参考.

关键词：平板式感应加热；电磁场；圆环电流；有限元分析；实验分析

DOI： 10.15938/j.jhust.2015.02.008

中图分类号：TM153+.1

文献标志码：A

文章编号：1007-2683（2015）02-0041-07

0 引 言

感应加热是热处理中自动化程度高、效率高、能耗最低的热处理技术，其特点是加热速度快，氧化脱碳少，工件变形小，无污染，易于实现局部加热和连续加热，便于实现机械化、自动化.中频或超音频感应加热电源的加热原理是靠感应线圈把电能传递到要加热的金属，然后电能在金属内部转化为热能.目前工业上感应加热多以线圈缠绕在料筒之上的形式广泛应用在拉丝机、吹膜机、造粒机、注塑机、挤塑机、热塑性塑胶管材、型材生产等加热领域，但是由于在平板式电磁感应加热技术领域中由于控制精度的不足和响应速度的缓慢，绕线方式对于磁场分布的干扰和钢板上面各点温度的一致性不易控制等难点，现在工业中平板式电磁感应加热技术大多应用在一些粗犷的恒温恒功率加热装置当中，这就对平板式电磁感应加热技术在温度控制的精度和响应速度上提出了更高的要求.本文主要讨论作为感应加热关键设备之一的感应圈中电磁场的分布情况，首先讨论圆环电流的磁场分布情况，然后以此为基础扩展到线圈的情况，其结果对感应圈的选择提供了理论根据，对感应热处理设备的配套有一定的作用.

1 平板式感应加热

1.1 现状及问题

感应加热国内发展起步较晚，而平板式感应加热的应用仅限于家庭烹饪等粗犷的加热环境中，而用于工业的精确可控的加热方面的研究还比较空白，我们目的就是完成对加热均衡性和控制精确性的研究，并将其应用于SMD等对加热环境要求较高的领域.

在研究中发现，利用传统的饼式线圈加热存在加热死区，如图1所示，所以本论文的目的就是研究饼式线圈的磁场分布，从而帮助我们了解加热时涡流的分布状况.

1.2 电磁加热的理论基础

1.2.1 麦克斯韦电磁场理论

表征电磁场的麦克斯韦方程组是整个电磁场理论的基础，它是由英国物理学家詹姆斯·麦克斯韦在19世纪建立的一组描述电场、磁场与电荷密度、电流密度之间关系的偏微分方程，方程组由4个定律组成，分别是安培环路定律、法拉第电磁感应定律、高斯电通定律和高斯磁通定律.求解电磁场实质就是以这些方程组为出发点来分析、研究与实验验证其中的各个参数.

1.2.2求解电磁场所需边界条件

求解电磁场需要设置边界条件，归纳为以下3种，分别是Neumann（诺依曼）边界条件、Dirichlet（狄利克雷）边界条件以及它们的组合.而电磁场微分方程的解，只有在边界条件和初始条件的限制下才有，这就是通常所说的边值问题和初值问题.

2 平板式感应加热线圈磁场的求解

2.1饼式线圈的简化

传统感应加热的饼式线圈，是以平面上的一个点为圆心，在这个平面上一圈一圈的缠绕而成，这样就可以把线圈看成是多个半径依次增大的圆环在同一个平面内环环相套而形成，因此，可以将线圈简化成单个圆环电流来研究，线圈的磁场就是多个圆环电流磁场的叠加.

2.2 圆环电流磁场分布的研究

圆环电流在空间的磁场分布是电磁学和电动力学的一个重要问题.用毕奥一萨伐尔定律可求得全空间的磁感应强度分布.

图2为一个在XY平面内以R为半径的圆环形电流，圆环关于Z轴对称，所以此电流激发的磁场也就以Z轴为对称轴，因而在求得YZ平面的磁场分布之后，全空间的磁场分布情况也可以类比得到.

dB是圆电流上任意电流元Id/在YZ平面上一点P（y，z）处激发的磁场元，根据毕奥‐萨伐尔定律呵得式中：R为电流元对原点的位置矢量；r为电流元到P点的位置矢量；r0为P点对原点的位置矢量，于是可以得到r=r0-R.

在直角坐标系中

电流元在P点激发磁场分别在X轴、y轴、Z轴上的分量可以通过把式（5）代人式（l）得到

分别对式（6）、式（7）、式（8）积分便可得到圆环电流在P点激发的磁场其中K（k）和E（κ）分别为第一类和第二类完全椭圆积分.

对于中心轴线上的磁场

圆环电流平面上的磁场

2.3 感应加热线圈的磁场分布

通过对圆环电流磁场的计算，运用叠加的思想，可以猜测出线圈磁场分布的大致情况：线圈产生的磁场，越靠近线圈，磁感应强度越大.在线圈平面上，其内部圆心处磁感应强度最小，沿径向靠近线圈感应强度逐渐增大，其外部沿径向远离线圈感应强度逐渐减小；在全空间，线圈附近磁感应强度最大，且圆环内侧略高于圆环外侧.

3 圆环电流及感应加热线圈磁场的仿真

3.1 圆环电流磁场的仿真

在这一部分中通过利用有限元软件的强大分析功能，对圆环电流的磁场分布进行仿真，可以直观的看到其分布情况.

这部分仿真使用二维谐波磁场分析方法，该线圈为圆形对称，产生的电磁场在线圈的任一竖直截而上是相同的，而对于截面上的电磁场是对称的，因此计算截面的1/4区域即可，建立的几何模型如图3所示.

整个模型共分为3个部分：线圈、空气与远场，并且分别使用PLANE53、带有CURR和AZ自由度的PLANE53、INFINIlO这3个单元来模拟这3个部分.分别赋予材料属性并划分网格，如图4所，所示

给线圈定义实常数并耦合线圈的电流白自由度，对y轴上所有节点施加磁力线平行边界条件，同时给线圈施加电压降载荷，之后进行求解.读人结果之后，观察磁场分布情况.分布如图5-7所示，

由仿真的结果可知，圆环电流产生的磁场，越靠近线圈，磁感应强度越大.在圆环平面上，圆心处磁感应强度最小，在全空间，圆环电流附近磁感应强度最大，且圆环内侧略高于圆环外侧.这与通过计算的结果猜想的分布情况一致.

3.2感应加热装置磁场的仿真

以上面的分析为基础，对平板式感应加热装置进行有限元分析.同样使用二维谐波磁场分析，由于对称，同样分析1/4部分，几何模型如图8所示，这个模型分为4个部分，与上面相比多了一个铁板，铁板使用PLANE53单元，其余与上面相同，赋予材料属性并划分网格后图如图9所示.

类似的，同样给线圈定义相应的实常数并耦合线圈的电流自由度，对Y轴上所有节点施加磁力线平行边界条件，同时给线圈施加电压降载荷，之后进行求解.读入结果之后，观察磁场分布情况.分布如图10-12所示.

由以上仿真可以得出，平板式电磁感应加热的饼式线圈产生的磁场也有类似的分布特性.在线圈平面，线圈中心处磁感应强度最小，在全空间，线圈附近的磁感应强度强度最大，量然在空间中加入了磁导率非常大的铁磁性材料之后，磁场在空间的分布情况发生了巨大的变化，但是磁场分布的趋势没有发生本质改变，依然与圆环电流磁场分布的大小趋势类似.由此可以推测，有磁场产生涡流并由涡流作用而产生热量的感应加热，在铁板上会出现加热死区.

4感应加热装置磁场的测量及数据的采集

4.1 直流模拟交流测量磁场

使用SS495A集成霍尔元件来测量感应线圈磁场，仪器连接如图13所示.

在本测量仪器中，SS3325起到为感应线圈提供稳定恒流源的作用，此电流产生感应磁场，95A型元件的工作电压由可调稳压源供给，数字万用表KETITHLEY2000用来实时测量霍尔元件的输出电压.给线圈中通以电流就可以利用直流电来静态的模拟交流电产生的磁场，将上图中的线圈进行相应的替换即可测量不同拓扑结构线圈的磁场分布特性.

3.2 试验方法及数据采集

参照图13连接实验器材，换上相应的椭圆形线圈并将其抽象为数学模型而后用上述方法测量其磁场分布，线圈与其数学模型如图14所示，

第1组实验是在椭圆线圈中以每次500mA的变化逆向通人恒定电流，电流变化范围是0-5.5A，起始电压为2.49991V，装置工作电压为4.98V，实验目的是测量距离图b1点上方21.49mm处的磁感应强度，测量数据如表1所示，

归纳表1数据，激励电流，的增大会促使线圈的感应强度B随之增加.这符合B与，的同有规律，也就验证了此测量方法的正确性，

第2组实验是测量磁场水平方向的分布情况.给定的起始输出电压为2.49992V，激励电流为3A，装置T作电压为4.99V，在线圈上方5cm处，从b2，点移动至b2，以每次改变lcm的方式在X轴上测量水平磁场的数值大小，对数据进行修正之后记录如表2所示，

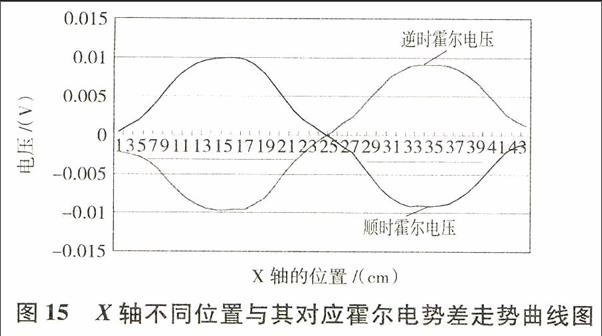
整理以上两表的数据，然后绘制X轴不同位置与其对应的霍尔电势差的走势曲线图，如图15所示.

归纳表2数据并观察曲线图，可以得出这样的结论：

1）分别通入正反向的直流电流能够反映交变电流的磁场分布情况，其磁场分布在径向上类似于正弦或余弦曲线，大小情况是中间及线圈外侧磁感应强度很小，主要集中在线圈及其附近，峰值出现在线圈当中.

2）实验的结果和仿真得出的结论“在线圈平面上，线圈中心的磁感应强度最小，沿径向逐渐增大，过了峰值之后，沿径向逐渐减小”一致.所以，由这个分布特性可以知道，涡流也会以这种方式分布在整块钢板上，所以采用饼式线圈的感应加热，加热死区必然会出现.

第3组实验是测量磁场在垂直方向上的分布情况，设置与先前相同的实验条件，在图14中的b.点，以每次lcm沿Z轴方向递增，分别记录通人正向与逆向的电流测量到的霍尔输出电压，如表3所示.

整理表3的数据并绘图，曲线图如图16所示，图中红线代表线圈中通入的是顺向电流，蓝线代表线圈中通入的是逆向电流，

总结表3数据并分析曲线图可以得出以下结沦：

1）线圈磁场在Z轴方向上随着距离的增加作非线性递减，衰减速度期初很快，随着距离的增大逐渐减小，到达一定高度时衰减趋于平缓，值也非常小，所以在工程实际中就必须控制铁板与线圈的距离以保证加热效果.

2）实验结果也验证了仿真的正确性，在全空问，线圈附近的磁感应强度最大，随着距离的增大，其值快速衰减.

4 结 语

通过理论计算、有限元分析和实验测量及对实验数据的整理得出，传统的平板式感应加热的饼式线圈磁场分布总是有这样一个趋势：在线圈平面，磁感应强度在线圈内部从线圈向圆心逐渐递减，圆心处为线圈内部的最小值，同时，磁感应强度在线圈外部从线圈向外逐渐递减，且向外向内磁感应强度衰减速度极快，磁感应强度的最大值出现在线圈附近，线圈内部的值略大于外部的值；在全空间，磁场主要分布在线圈附近，以线圈为中心在空问上向外衰减且衰减速度极快，由于饼式线圈的磁场分布存在这样的特性，所以在使用饼式线圈的平板感应加热装置对工件等进行加热时，加热部分——铁板，一定会存在加热的死区.

因此，在加热精度和加热均匀程度要求较高的场合，我们就需要改进线圈和平板的结构、优化影响加热的参数和采用更好的控制策略等来尽量达到加热精度和均匀程度的要求.