小型无人机航路规划及自主导航算法研究
2015-07-20蒋志华陶德桂
蒋志华,陶德桂
(中国人民解放军92419部队,辽宁 兴城 125106)
在20世纪90年代由美国主导的海湾战争和科索沃战争中,无人机卓有成效地执行了多种军事任务,其突出的战绩令世界各国刮目相看[1]。随着高新技术的发展,各国相继投入巨资发展无人机产业以满足军事需求和其他领域的应用,我国近年来更是迎来无人机发展的井喷期。军事领域是无人机应用的主要领域,军用无人机的主要用途包括:战术侦察和地域监视、目标定位和火炮校射、电子侦察和干扰、空中通信中继、战况摄录和态势评估、靶机和实施攻击等[2]。针对执行不同的使命任务,无人机可选择不同的飞行模式,包括遥控飞行模式、程控飞行模式、自主导航飞行模式以及它们的组合飞行模式等,其中作为靶机的无人机要求其具有航路规划和自主导航飞行功能,使其能按照预先装定的航线精确飞行。某小型无人机采用GPS接收机设计了自主导航系统实现了上述功能。
1 航路规划设计
该小型无人机采用的是程控+遥控+自主导航的飞行模式,可通过遥控指令在后两种飞行模式间进行切换。无人机起飞并经过一段时间的程控飞行后自动转入自主导航飞行模式。当自主导航飞行模式下的无人机高度不满足任务要求时,可以通过发送遥控指令对无人机的飞行高度进行调整,调整完后重新选定需要进入自主导航飞行模式下的航点号,并切回自主导航飞行模式继续飞行。自主导航的基本设计思想是利用无人机机载GPS接收机接收到的位置信息作为无人机的当前位置,通过计算准实时求得无人机偏离预期航线的侧偏距及侧偏距的变化速率,根据导航控制律解算出舵翼偏角,经由飞控系统产生指令控制副翼动作,从而修正飞行航迹,最终消除侧偏距。为此,需要在飞行前规划好航路并装定存储在无人机内。由于GPS系统采用的是WGS⁃84坐标系[3],为了描述无人机自主飞行的运动轨迹和飞行状态,必须选用适当的导航坐标系。考虑到小型无人机的飞行距离和可用GPS接收机的精度,定义如下二维导航坐标系:起飞点为坐标原点,x轴为正东方向,y轴为正北方向,单位为m,则WGS⁃84坐标系转换为导航坐标系的公式为[4]:
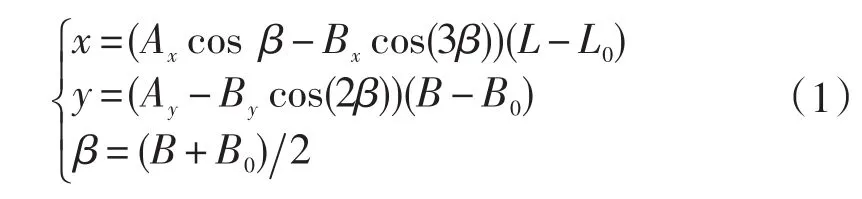
式中:(L0,B0)、(L,B)分别为导航坐标系原点及无人机当前位置在WGS⁃84坐标系下的经度和纬度值,由GPS接收机获取,单位为rad,Ax=6 383 487.606 m,Bx=5 357.31m,Ay=6 367 449.134m,By=32 077.0m。
预期飞行航线通常是由直线段和圆弧段组成,装定的飞行航线数据则为飞行航线中的一些特征点,简称航点,其结构为:
typedef struct_flypoints{
int nPt; 航点号
double dLon; 经度
double dLat; 纬度
double dR; 半径(直线段为0,圆弧段不为0)
double dArc;
圆弧角(左转为正,右转为负)或航向角(直线段)
}flyPoint;
这样,就可以定义一条由N个点组成的航线fly⁃Point flyPt[N],如果当前航点n(n<N)经由直线到达下一航点n+1,则当前航点的半径和圆弧角均为0,如果当前航点n经由圆弧到达下一航点n+1,则该段圆弧与由航点n-1和航点n组成的直线段和由航点n+1与航点n+2组成的直线段相切,如图1所示。
在设计圆弧段航线时应确保其半径大于无人机的最小转弯半径,无人机的转弯半径可采用以下方法计算:假设飞行空速为v,转弯倾斜角为γ,则协调转弯半径为[5⁃6]一条完整的航线还应该包括起点和终点,通常起点即为发射点,而终点则应该是回收点,在自主导航飞行模式下,无人机飞到终点附近后将自动执行停车开伞指令。以上航点数据是录入时的格式,为了减轻飞行解算时的CPU负荷,提高自主导航的实时性,这些数据在录入时通过程序及时转换为导航坐标系下的数据并进行存储,其存储格式与上述格式类似,只是经、纬度值变为导航坐标系下的横、纵坐标值,直线段的航向角经由以下公式计算得到(真北为0°):

图2为一条典型的飞行航线示意图。
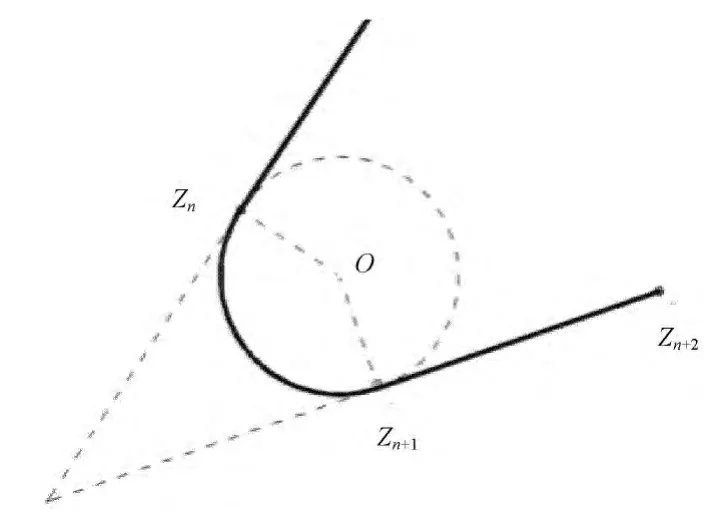
图1 圆弧段与直线相切

图2 典型飞行航线示意图
2 导航系统设计
对于该小型无人机,选用数据刷新率为5 Hz的机载GPS接收机,无人机飞行速度约为200 m/s,导航系统的控制律解算周期取20 ms,则在一个解算周期内,无人机飞行距离约为4m,考虑GPS单点定位精度及飞控系统和气动力反应时间,无人机的飞行误差可以控制在100m之内,能够满足精度要求。由于起飞前机载设备已经加电并处于正常工作状态,GPS接收机正常输出数据,导航系统中存放的数据会不断刷新,但GPS接收机的数据更新周期大于导航系统控制律解算周期,且当无人机进行机动飞行时,可能会出现GPS接收机的信号中断或者不连续的情况,则GPS信号不能准确反应无人机的实时位置,需对无人机的当前位置进行推算,可采用两点式航路推算公式近似计算,其计算方法如下:
设飞机在tM时刻和tN时刻的GPS位置数据分别为(LM,BM)和(LN,BN)(注意:tM<tN,tM时刻和tN时刻可以直接从GPS接收机的输出信息中获取),转换为导航坐标系下的位置分别为(xM,yM)和(xN,yN),自tN时刻开始计时,则t时刻无人机的位置(xt,yt)可计算为:
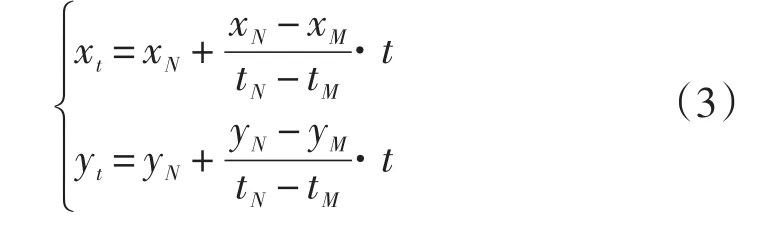
由此可见,导航系统至少需要保存两组最新得到的GPS数据信息,为了减小误差,可以保存更多组最新得到的GPS数据信息,比如10组,分别为tN-9,tN-8,…,tN-1,tN时刻的GPS位置数据,则可取tM=tN-9。
GPS接收机正常工作与否直接关系到无人机自主导航的飞行精度,在GPS接收机短暂失效的情况下虽然可以按上述公式进行位置推算,但随着中断或不连续时间的延长,积累误差会越来越大。解决这种问题的办法可以通过采用高品质的GPS接收机或者增加GPS接收机备份的措施,也可以设置当GPS信号中断时间超过某一数值后自动在原地盘旋,或者转入遥控飞行模式通过外测手段获取无人机地理位置信息完成任务。
3 控制律设计
该小型无人机导航控制律采用常用的比例微分控制,导航的目的就是使飞机能按预定航线飞行,不会出现偏离航线现象。当飞机偏离航线时,导航计算机就会根据设计的控制律计算出相应的偏转舵角,交由飞控计算机控制副翼舵执行偏转动作,使飞机重新回到预定航线飞行。除此之外,设计的控制律还应保证飞机能在各种可能情况下准确地进入航线。副翼舵的偏转大小和方向又与飞机当时的速度v、偏航距d以及航迹角误差Δψ有关,在直线飞行段时其控制律可采用偏航距d和飞机速度垂直航线的速度分量d v来设计:

式中速度垂直于航线的分量dv事实上就是飞机到航线距离的一阶微分。因此,式(4)正是飞控系统中常用的比例加一阶微分式控制律[7⁃8],其中Δδa为副翼舵偏角,规定其使飞机向左转为正,向右转为负;当飞机在航线右侧偏航时,偏航距d为正,否则为负;Δψ=ψ-ψi(ψ为GPS实时测得的当前无人机飞行航向角),右偏为正,左偏为负;k1和k2为比例系数且均大于0,调整其大小可以改变副翼舵变化的灵敏度。
当无人机进入圆弧段飞行时,则可以利用航点的转弯半径和公式tgγ=v2(Rg),通过查表法得到转弯倾斜角,此即为副翼舵偏角,其正负参考该航点的圆弧角正负值确定。查表法较之解算超越函数arctg()运算速度更快,且减少CPU运算量。
4 算法实现
要实现控制律算法,首先需要计算飞行偏航距。航线一般包括直线段和圆弧段,当要求无人机沿着直线段飞行时,应该首先判断无人机是否在该直线段范围内,如果无人机处于该线段的两侧延伸范围,则按照点到直线的距离公式所计算的偏航距肯定不符合实际情况。如图3所示,当无人机当前位置Z处于直线段Zn-1Zn范围外时,则∠ZZnZn-1>90°,否则∠ZZnZn-1<90°,为了避免解算超越函数arccos(),通过计算判断即的关系就可知道无人机是否飞出直线段Zn-1Zn范围外了。
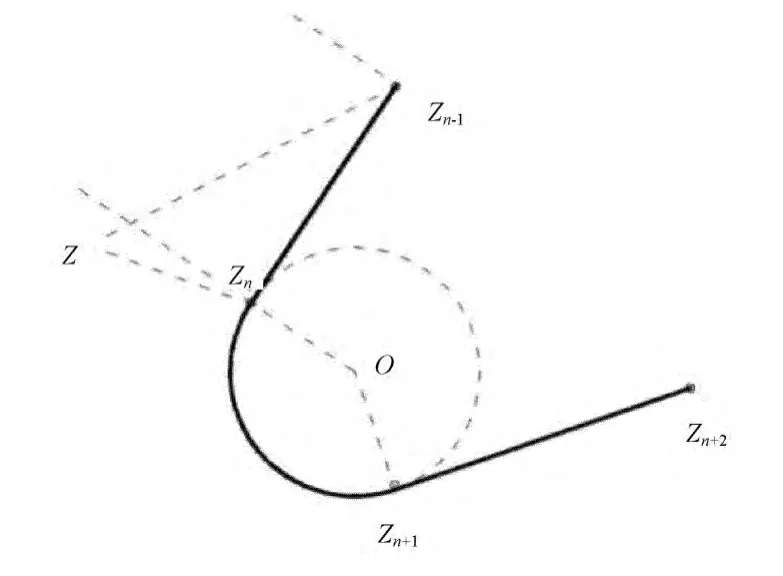
图3 当前位置Z处于直线段Zn-1 Zn范围外的情况
当确定无人机当前位置处于直线段范围内时,可以通过如下方法计算与直线段的偏航距:
对于航线中的直线段,采用以下直线方程表示:
Ax+By+C=0
假设Zn-1(xn-1,yn-1)、Zn(xn,yn)为航线直线段的两个端点坐标,则 A=yn-1-yn,B=xn-xn-1,C=xn-1yn-xnyn-1,无人机从Zn-1点飞向Zn点,无人机当前的位置为Zt(xt,yt),则偏航距为[9]:
式中:sign(B)为取符号函数,下同。
当无人机处于圆弧段飞行时,其偏航距与在直线段时的计算方法是不一样的。如图3所示,已知Zn点的航点数据,可以求出圆心O的坐标,其计算公式为:
当 |xn-xn-1|>0.1时,
则圆心O的坐标为O(xo,yo):

当前点Zt(xt,yt)的偏航距为:

当 | xn-xn-1|≤0.1时,则可认为直线方程为x=xn-1=xn,此时k1=0,上述公式仍然有效。
为了避免超越三角函数的计算,在判断无人机是否飞出圆弧段时可采用计算无人机是否进入到下一直线段范围内的方法完成,其计算方法同上。根据控制律公式,还需要计算偏航距的微分[10]。对于直线段,可根据公式 dv=v·sin(Δψ)(其中 Δψ 为航迹偏差角),对于圆弧段可以采用其离散近似公式代替[11]:dv=Δd Δt=(dt-dt-1) Δt,其中dt和dt-1分别表示当前时刻和前一时刻的偏航距,Δt为采样间隔时间。
5 结语
某小型无人机采用比例微分式导航控制律设计,控制机理成熟可靠。其对于航线的确定、偏航距及其微分的计算等都采用了较为理想的算法。同时,它应用GPS全球定位系统的定位信息,定位精度和可靠性大幅提高;这些设计方法和措施提高了该无人机的自主导航控制精度和稳定性,使其具有良好的飞行品质。
[1]邹湘伏,何清华,贺继林.无人机发展现状及相关技术[J].飞航导弹,2006(10):9⁃14.
[2][美]法斯多姆.无人机系统导论[M].吴汉平,译.北京:电子工业出版社,2003.
[3]袁建平,方群,郑谔.GPS在飞行器定位导航中的应用[M].西安:西北工业大学出版社,2000.
[4]屈蔷,梅劲松,袁家斌.小型无人机GPS自主导航算法的研究与实现[J].大众科技,2006(3):47⁃48
[5]祝小平.无人机设计手册[M].北京:国防工业出版社,2007.
[6]贾玉红.航空航天概论[M].北京:北京航空航天大学出版社,2013.
[7]刘亮亮,胡延霖,易牧,等.无人机半实物仿真系统研究[J].兵工自动化,2008,27(3):44⁃45.
[8]梁振东,李华英,管军.小型无人机SINS/GPS组合导航系统研究[J].科学技术与工程,2013,13(3):290⁃295.
[9]郭锁凤.先进飞行控制系统[M].北京:国防工业出版社,2003.
[10]吕晓林,罗纯哲.无人机低空小捷径飞行研究[J].宇航计测技术,2013,33(6):84⁃87.
[11]王昱辉,雷金奎,田力.基于SmartFusion的无人机飞行控制系统设计[J].现代电子技术,2012,35(10):137⁃139.
