船用高功率密度永磁发电机损耗及温度场计算

杜翔宇，胡 萌，胡嘉磊，李旭光

（上海交通大学，上海 200240）

0 引言

船舶电力系统的规模与容量随着船舶行业的不断发展而升级，船用发电机的容量也相应提高。永磁同步发电机具有功率密度高、效率高、结构简单的优点[1]，相较于其他种类电机更加适于应用在船舶电力系统中。

船用永磁同步发电机的工作环境较为恶劣。海上空气湿度较大，同时空气中盐分较高，因而需要船用发电机对湿热、盐分、霉菌有较高的耐受能力[2]。同时，由于湿度较大，极大地降低了空气的散热能力，而过高的工作温度，会造成永磁体的不可逆退磁，因而需要保证永磁发电机的工作温度保持在适宜的范围内。因此船用永磁同步发电机的损耗及温度场计算对保证其正常运行有着重要意义。

国内外学者对船用高功率密度永磁发电机的温度场分布进行了大量研究。2001年M·Negrea研究了一台用于船舶推进系统的径向磁通永磁同步电机，并在确定了冷却系统的情况下，对电机进行了二维的电磁场分析和三维温度场有限元计算[3]。2005年，周峰等人通过有限元法对定子通风沟内流体流动及热交换进行了研究，并对定子部分进行了温度场计算[4]。2008年，JNerg采用T型集总参数模型对高功率密度径向磁通电机的温度场进行了热分析，特别考虑了不同转速下气体的对流换热[5]。2011年，李伟力对高功率密度、高压永磁同步电机整体温度场进行了研究[6]。然而，当前研究通常仅针对电机的一部分进行温度计算，忽略了电机各个部分之间温度场的影响；同时，将温度场的计算与流场的计算分开计算，忽略了实际中流场与温度场之间的耦合情况，流体的传热过程与实际情况可能存在差距。

本文针对一台260 kW高功率密度永磁同步发电机进行流场⁃温度场分析。首先通过建立二维有限元模型，采用时步有限元方法计算电机电磁损耗，根据损耗确定热源，然后建立三维流场⁃温度场耦合模型，通过计算水套流场温度，计算等效散热系数，从而实现流场⁃温度场耦合，进而得到电机内部温度分布，最后分析了冷却水流速对电机温升的影响。

1 永磁电机电磁损耗计算

永磁电机的电磁损耗包括定子铁耗、转子涡流损耗与定子铜耗。当前，对于中小型电机，定子铜耗可以通过常规的工程计算方法进行准确计算，本文不再赘述。定子铁耗与转子涡流损耗的计算较为复杂，是当前研究热点之一。目前，通常通过有限元计算的方法对定子铁耗和转子涡流损耗进行计算。

1.1 永磁电机定子铁耗计算

本文采用等效椭圆法对定子铁耗进行计算。首先，通过有限元法计算各个单元节点的矢量磁位A，进而求取磁密B、磁场强度H等其他场量，依据这些场量求取定子铁耗。将铁耗进行分离[7]，可得：

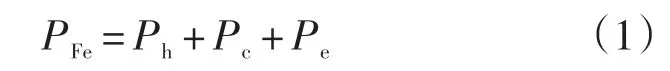
式中：Pk为磁滞损耗；Pc为涡流损耗；Pe为附加损耗。

静态磁滞回线中，可以将磁场H分解为可逆分量Hrev与不可逆分量Hirr，则磁滞损耗可以表示为：

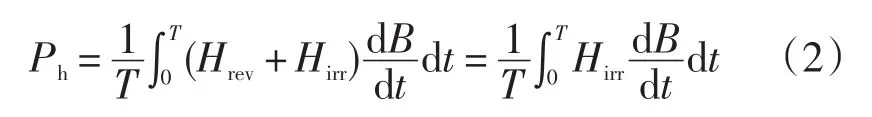
通过时步有限元方法，计算并记录每个单元的磁密波形，根据该波形绘制等效椭圆，从而计算可逆分量Hirr[8]，则瞬态磁滞损耗为：

瞬态涡流损耗为：

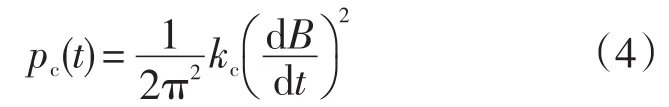
瞬态附加损耗为：

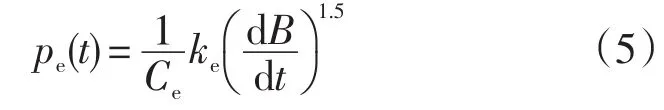
1.2 永磁电机转子涡流损耗计算

虽然永磁同步电机中，普遍认为转子与空间磁场同步旋转，然而，空间磁场会因为定子开槽等原因存在谐波。因而，在电机转子中仍会存在涡流损耗。通过有限元方法计算涡流损耗[9]，假设材料均匀、各向同性，并且忽略位移电流、端部效应，则可将电机模型简化为二维有限元模型进行计算。模型中电流密度与矢量磁位仅含z轴分量，将垂直于电机轴的平行平面场域Ω上的电磁场问题表示为边值问题：

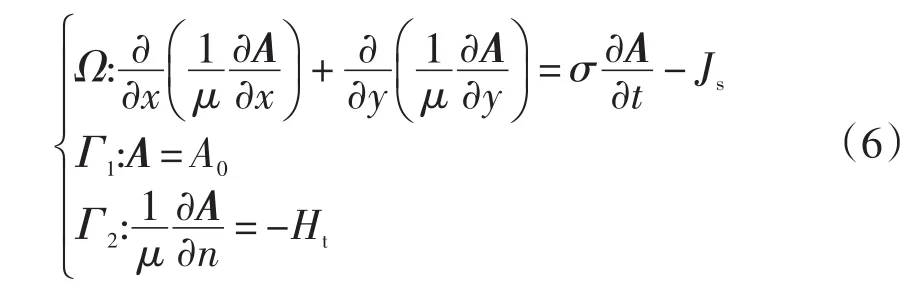
式中：μ为磁导率；A为矢量磁位；σ为导电材料电导率；Ht为永磁材料矫顽力；Js为源电流密度；Γ1，Γ2分别表示第一类和第二类边界条件。则涡流密度为：

转子旋转部件的涡流损耗为：

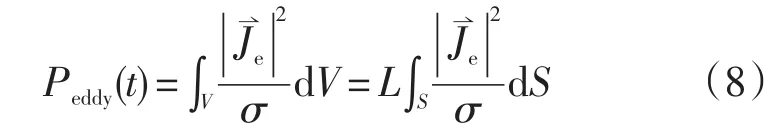
式中：S为涡流切面面积；L为部件的轴向长度。

2 永磁电机流场⁃温度场计算

通过计算电机损耗，可以确定电机内部热源的分布。虽然通过给定相应的边界条件，可以同时求解流场与温度场，但采用该方法对计算机的处理能力要求很高，目前尚不现实。

本文首先对流场进行计算，通过流场计算得出的流体流速，转换为流体与固体界面的散热系数，然后计算相应的温度场，上述过程进行多次迭代直至流场、温度场计算结果均收敛。该过程将流场与温度场进行耦合计算的过程转为顺序计算，从而降低耦合场计算需求。

2.1 冷却系统流场⁃温度场耦合计算

电机冷却结构由定子铁心外水套与风套组成。水套与电机定子紧密接触，辅助电机定子进行散热；电机转轴安装轴流风扇，通过转子通风孔对电机转子部分进行空气散热，形成循环风套，其热量也通过水套进行吸收。建立三维模型，并通过商业有限元软件FLUENT进行计算。

为了简化计算，对计算模型做出以下合理假设：

（1）忽略风套外壁的自然对流散热；

（2）忽略水套与风套中焊点等不规则区域；

（3）材料热物理特性稳定，不随温度变化而变化。

由于水套中流体的温度不均匀，无周期性规律，不能对其进行周期性分解。

水套流场⁃温度场耦合计算的边界条件为：

（1）环境温度298.15 K（25 °C）；

（2）水套入水口流速1m/s，初温298.15 K；

（3）水套外表面热通量。

流场主要为气体与液体流场，假设上述流体不可压缩，并且忽略重力对流体的影响，则各个节点的能量、动量与质量是守恒的。因此，流场计算的约束方程为以下形式[10]：

质量守恒：

动量守恒：

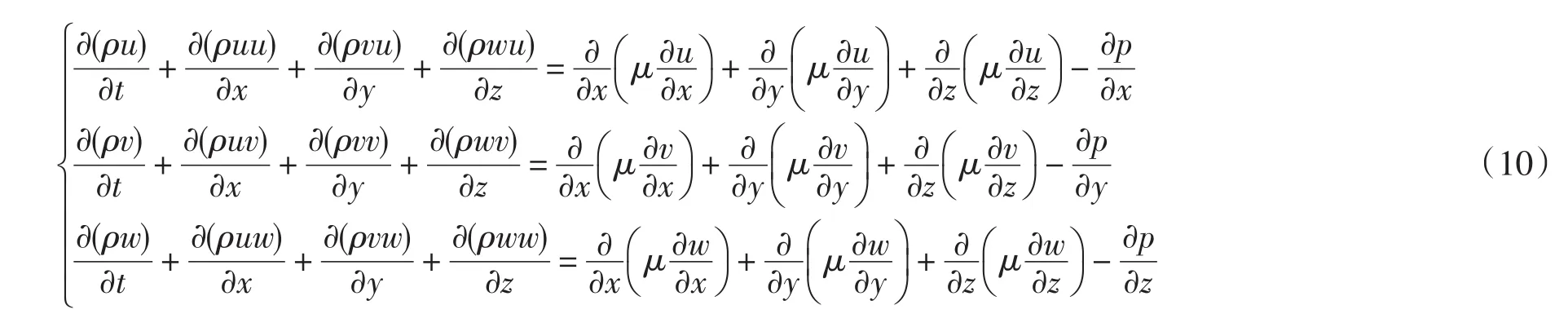
能量守恒：

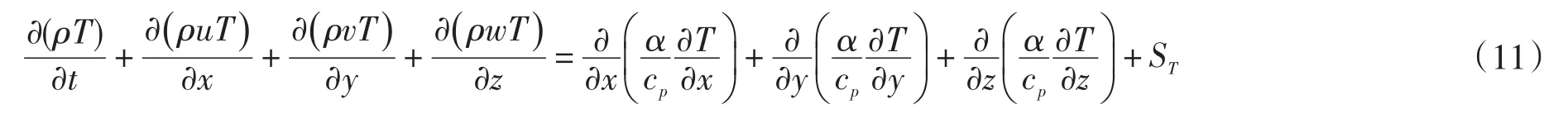
2.2 电机温度场计算

与冷却系统计算不同，电机结构满足周期性的规律，同损耗计算类似，可以对其1 4模型进行简化的计算，以提高计算速度。

通过水套流场⁃温度场耦合计算，将水套对电机的散热转化为散热系数，其等效的散热系数为[11]：

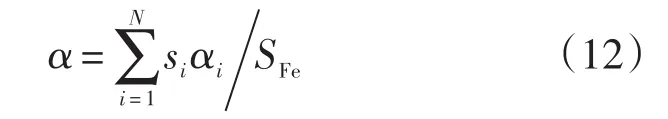
式中：si为冷却水道内壁单元面积；αi为内壁单元的散热系数（通过数值计算方法求解水套流场获得），SFe为定子铁心外圆面积。从而将水套的冷却作用等效为对流散热面，将计算进行简化。

电机温度场计算的边界条件为：

（1）水套1 4模型内壁等效散热系数，由水套流场⁃温度场耦合按照式（12）计算得到；

（2）水套1 4模型内壁附近等效对流换热介质温度，取水套流场⁃温度场计算得到的最大冷却水温度；

（3）电机1 4模型各结构生热率为损耗计算得出的各结构损耗。

根据损耗热源，与散热系数，对电机的温度场进行计算。热传导方程为：

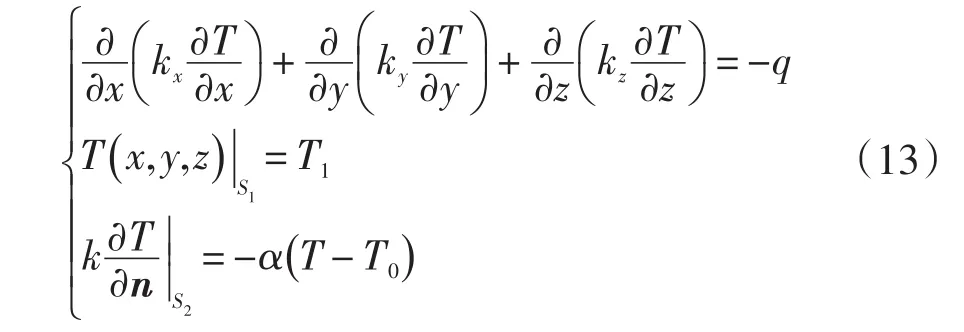
式中：T为边界上已知的温度值；T0为边界S2周围介质的温度；kx，ky，kz分别为 x，y，z方向的导热系数（单位为W/m·K）；q为热源密度（单位：W/m3）；α为边界S2上的表面散热系数；k为边界S2法向导热系数；T1为边界S1上的给定温度，n为边界面S1和S2上的法向矢量。

3 结果分析

本文对260 kW高功率密度永磁同步发电机进行了温度场仿真计算，样机的基本参数如表1所示。

表1 260 kW样机基本参数

3.1 损耗计算结果

通过商业有限元软件Maxwell建立样机的二维模型，根据电机的对称性，对其1 4模型进行分析计算，稳定运行状态下的磁密分布计算结果如图1所示。

图1 260 kW样机磁密分布计算结果

根据磁密分布，通过时步有限元方法，计算各个元件的电磁损耗。图2为各部分损耗随时间变化的曲线。稳定运行时，定子铁耗的总损耗为1 322W，转子涡流总损耗为566W。

3.2 样机流场⁃温度场耦合计算结果

3.2.1 水套流场⁃温度场耦合计算结果

设水流流速为1 m/s，入水口水温为25℃，电机损耗产生的热量完全由水套吸收，则水套的热通量为：H=电机总损耗(W )水套外表面面积（m2）=7 5521.212 3=6 229.48W/m2。

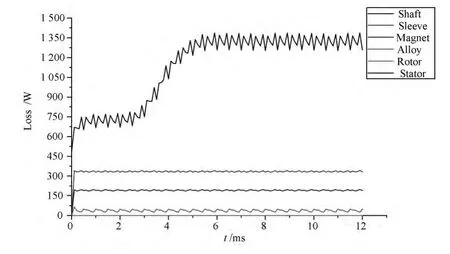
图2 样机各部分损耗计算结果

水套流速计算结果如图3所示。由于水套结构曲折，水套流速不均匀，并在弯道处形成涡流，导致水套温度场分布不均匀。水套内表面温度场分布如图4所示，可以看出，水套中涡流区域由于冷却水滞留，其热量也随冷却水滞留，因而温度较非涡流区域高。

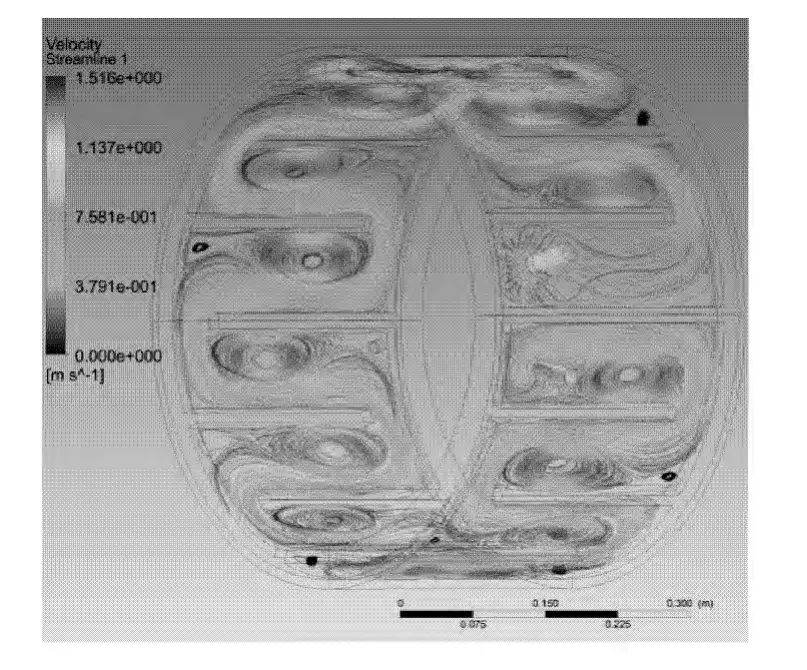
图3 冷却水流速度场

图4 水套内壁面温度分布

3.2.2 电机本体温度场计算

图5为电机本体温度场计算结果。由图5可见，绕组部分温度较高，而由于风冷系统的存在，靠近风扇的绕组部分温度远低于远离风扇的一端。

图5 样机本体固体区域温度分布

样机各部分温升计算结果如表2所示。由表2可知，电机本体中绕组端部温升最高，这是由于绕组端部未与定子铁心接触，仅可通过风套进行冷却，导致其散热效果较差。

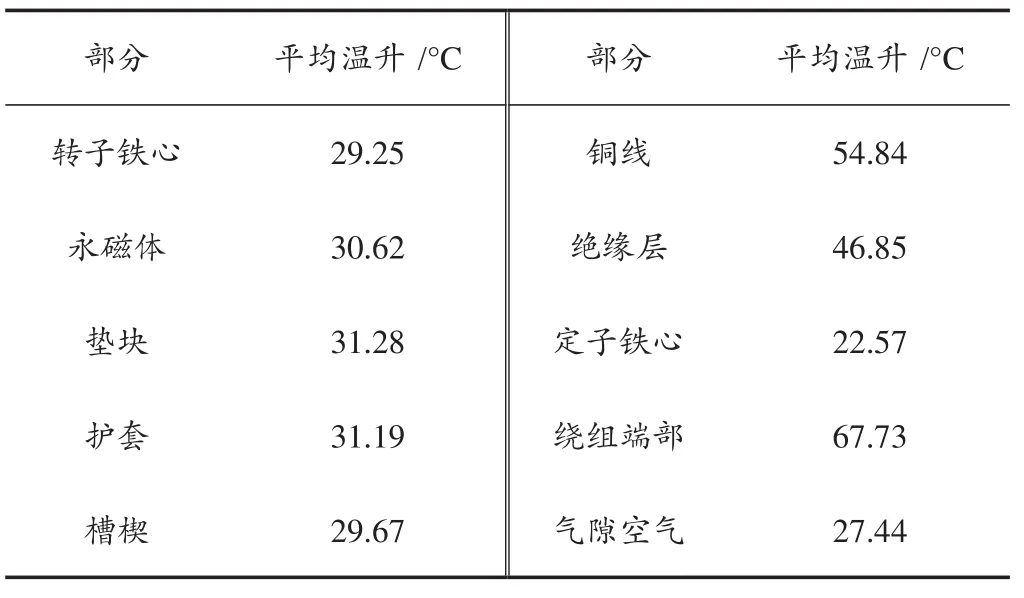
表2 260 kW样机本体各部分平均温升（1 m/s，25°C）

3.2.3 水套入口流速与温升关系计算

改变水套入口端冷却水流速，重复上述计算过程，可以得到一系列电机各部分温升随流速变化的结果，如图6所示。

图6 260 kW样机各部分平均温升随水套入水口流速的变化曲线

由图6可知，电机各部分温升随水套流速增加而降低，当流速大于2m/s时，温升随流速增加的变化趋于稳定，因而，对样机的水套冷却系统，将流速控制在2m/s左右较为理想，可以为水套冷却系统水泵选择的依据之一。

4 结语

本文采用有限元软件Maxwell，计算了船用高功率密度永磁同步发电机各部分的电磁损耗，作为电机温度场计算中的热源，同时用Fluent软件计算水套中流体的等效散热系数，实现流场⁃温度场的耦合计算，得到电机本体温度场分布。电机水套与本体的耦合场，特别是温度场的计算结果对永磁同步发电机的本体与冷却系统设计有一定参考价值。水套温度场计算结果显示，水套中也存在涡流，其温度场分布并不均匀，且涡流区域温度较高，散热情况不佳，因而水套设计原则上应考虑减小涡流。电机本体温度场计算结果表明，温升最高的部位在绕组端部，在电机设计时应当进行针对性处理。最后计算得到冷却水流速与电机温升关系曲线，表明对该型电机，冷却水流速为2m/s时最为合理。

[1]唐任远.稀土永磁电机发展综述[J].电气技术，2005（4）：1⁃6.

[2]寿海明，冀路明，马守军.现代船用推进电机技术研究[J].船电技术，2007，27（1）：36⁃39.

[3]NEGREA M，ROSU M.Thermal analysis of a large permanent magnet synchronousmotor for different permanentmagnet rotor configurations[C]//IEEE 2001 International Electric Machines and Drives Conference.Cambridge，MA：IEEE，2001：777⁃781.

[4]ZHOU Feng.Numerical calculation of 3D stator fluid field for large electricalmachine aswellas influenceson thermal field dis⁃tribution[J].Proceedingsof theCSEE，2005，25（24）：128⁃131.

[5]NERG Janne， RILLA Marko，PYRHONEN Juha.Thermal analysis of radial⁃flux electrical machines with a high power density [J]. IEEE Transactions on Industrial Electronics，2008，55（10）：3543⁃3554.

[6]LIWei⁃li.Analysis on solid rotor 3⁃D temperature field in high voltage PMSM[J].Proceedings of the CSEE，2011，31（18）：22⁃25.

[7]BERTOTTIG.Space⁃time correlation properties of themagneti⁃zation process and eddy current losses[J].Journal of Applied Physics，1983，54（9）：5293⁃5305.

[8]Lin D，Zhou P，Fu W N，et al.A dynamic core lossmodel for soft ferromagnetic and power ferritematerials in transient finite element analysis[J].Magnetics，IEEE Transactions on，2004，40（2）：1318⁃1321.

[9]王晓远，李娟，齐立晓，等.盘式永磁同步电机永磁体内涡流的有限元分析[J].微电机，2007，40（1）：5⁃9.

[10]王福军.计算流体动力学分析⁃CFD软件原理与应用[M].北京：清华大学出版社，2004.

[11]XIA hai⁃xia，TAO Li，NIGuang⁃zheng.Analysis of ventila⁃tion fluid field and rotor temperature field of a generator[J].Electric Machines and Control， 2007，11（5）：472⁃477.