一种改进的K⁃Modes聚类算法

石隽锋，白妙青

（山西大学 计算中心，山西 太原 030006）

0 引言

聚类技术广泛应用于数据挖掘、统计模式识别、机器学习、信息检索等领域[1⁃2]。它是将一个数据集划分为若干个子类，使得类内对象尽可能相似，类间对象尽可能相异[3]。随着分类型数据的出现，分类型数据聚类成为亟待解决的问题。K⁃Modes算法[4]是在K⁃means算法[5]基础上扩展而来的，其算法简单、高效，被广泛应用于各个领域，但是它采用在每个属性域中采用频率较高的属性值作为类中心，其他数据和类中心进行0⁃1匹配，确定它们所属的类别，以及目标函数中各数据和类中心的距离也是0⁃1匹配，这些显然是不合理的。

人们针对该问题进行了改进，白亮等人提出了基于新的距离度量的K⁃Modes算法，在选取类中心时，能够较精确计算对象的距离，从而更精确地选取初始类中心，提高了算法的执行效率[6]。文献[7]提出了基于频率的加权度量方法，有效地提高了算法的聚类效果。Ng等人利用基于相对频率的相异度度量对传统的K⁃Modes聚类算法进行了改进，有效地提高了算法效率[8]。文献[9]采用新的相异度度量方法改进K⁃Modes算法，有效地提高了算法性能。然而这些算法都隐含假定类中各数据对象具有一样的重要性，没有充分考虑分类型数据的特点，因而不能准确计算数据间的距离。文献[10]采用期望熵来判断各种分类方案的好坏，它依序处理数据，并对分得不好的数据重新标记类别。

本文提出了改进的K⁃Modes算法，将期望熵引入到K⁃Modes算法中来，采用期望熵最小的方法对各数据归类，并且定义了基于期望熵的目标函数，在选择初始类中心时，通过简单0⁃1匹配选取最不相同的数据作为类中心。这些改进可以将分类型数据更有效地归类，从而提高了算法的效率。

1 传统K⁃M odes聚类算法

K⁃Modes聚类算法是通过对K⁃Means聚类算法的扩展，使其应用于分类属性数据聚类。它采用简单匹配方法度量同一分类属性下两个属性值之间的距离，用Mode代替K⁃Means聚类算法中的Means，通过基于频率的方法在聚类过程中不断更新Modes。

定 义 1[4]：设 S=( )U,A是一个分类信息系统，U={x1,x2,…,xn}，A={a1,a2,…,am}，xi,xj∈U(1≤ i,j≤ n)，xi,xj分别被A描述为 xi=(f(xi,a1),f(xi,a2),…,f(xi,am))和xj=(f(xj,a1),f(xj,a2),…,f(xj,am))，xi和 xj的距离定义为：

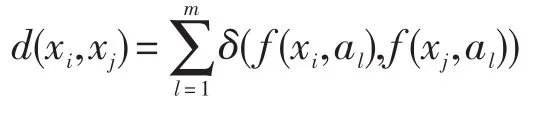
式中：

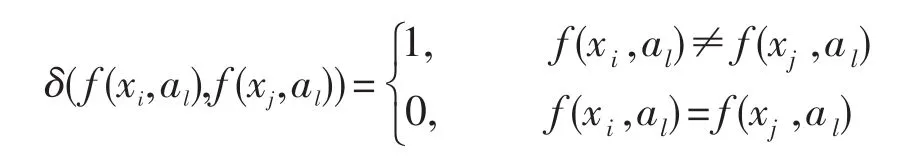
Huang为实现K⁃Modes聚类算法定义目标函数为[4]：

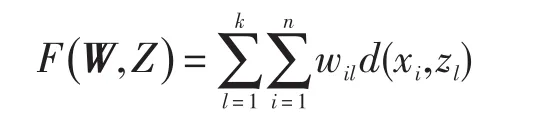
式中：

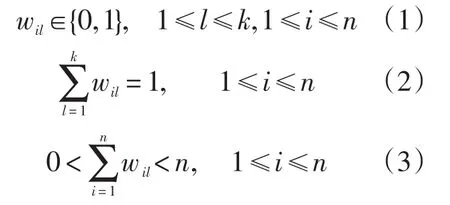
W 是一个n×k的{0，1}矩阵；n表示对象集U所包含的对象个数；k表示聚类的个数，wil=1表示第i个对象被划分到第l类中，Z={z1,z2,...,zk},zl(1≤l≤k)是第l类的中心。

为了使目标函数F在满足约束条件式（1）～式（3）下达到极小化，K⁃Modes聚类算法基本步骤如下：

Step1：从数据集中随机选择k个对象作为初始类中心，其中k表示聚类个数；

Step2：应用简单匹配方法计算对象与类中心（Modes）之间的距离，并将每个对象分配到离它最近的类中去；

Step3：基于频率方法重新计算各类的类中心（Modes）；

Step4：重复上述Step2，Step3过程，直到目标函数F不再发生变化为止。

2 改进的K⁃M odes算法

K⁃Modes聚类算法利用简单匹配方法对每个对象分类必然效果较差，因为用频率来选取类中心比较粗糙，再用0⁃1匹配决定所属类别也不太合理。文献[9]提出了基于期望熵（Expected Entropy）的分类方法比较适合分类型数据，因此，这里将该方法结合到K⁃Modes算法中来，进一步提高算法的运行效率。期望熵的定义如下：

定义2：设 S=(U ,A)是一个分类信息系统，U={x1,…,xi,…,xn}，A={S (a1),…,S(aj),…,S(am)}，S(aj)表示第 j个属性所有属性值的集合，数据对象xi可表示成xi={xi1,…,xim}，假定分为k类，C={c1,…,cl,…,ck} ，期望熵的定义如下：

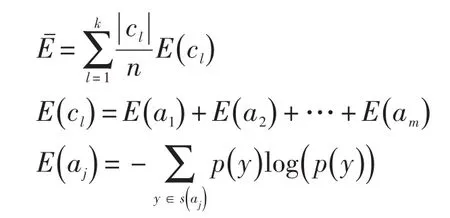
假定三个数据对象，v1={" red","heavy"},v2={"red","medium"},v3={" blue","light"}要分为两类，有三种分类方案如表1所示。

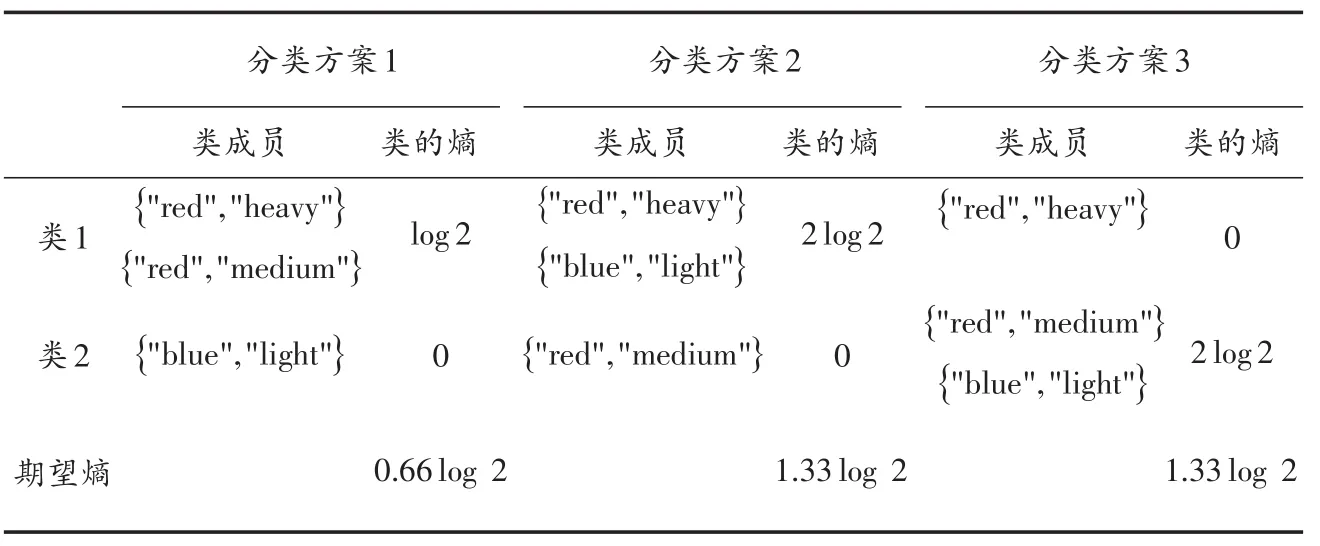
表1 对数据集{v1，v2，v3}不同的分类方式及期望熵

从表1可以看出，分类方案1的期望熵最小，该分类方案也是最好的分类方式。因此，可以将期望熵作为目标函数。同时，确定了类中心后，对每个对象分类也可以采用该方法，假定初始类中心为：{" red","heavy"}，{"blue","light"}，向量{" red","medium"}有两种归类方式，即方案1和方案3，方案1的期望熵较小，并且该方案是较好的分类方式，因此，可以通过取最小期望熵对每个对象进行分类。

另外，在数据集中随机选取类中心也不合理，假定选取的类中心在一个类中，将其他对象归到这k个类中，重新计算各类中心，再次归类，可能使得目标函数不再变化，得不到好的聚类效果，如图1所示。假定数据集中有四个对象，选取数据1，2作为初始类中心，将数据3和4归类后，新的类中心为数据5，6，再次对四个数据归类，分类结果可能不变，目标函数不再发生变化，而该分类结果并不是理想的分类结果。因此，初始化时，应找到k个最不相同的数据作为初始类中心。首先找到最不相同的两个数据 xc1，xc2，使得，分别作为两个类的中心，再依次找到其他类中心，假定已经找到了 j-1个类中心，第j个类中心为xcj，使得当数据集比较大时，先取样再寻找类中心。

图1 经典K⁃Modes算法错误的分类情况

改进的K⁃Modes聚类算法基本步骤如下：

Step1：从数据集中选择k个最不相同对象作为初始类中心，其中k表示聚类个数；

Step2：应用期望熵最小方法将每个对象分类；

Step3：基于频率方法重新计算各类的类中心（Modes）；

Step4：重复上述Step2，Step3过程，直到目标函数F不再发生变化为止。

3 实验分析

下面分别从分类正确率（Accuracy）、类精度（Preci⁃sion）和召回率（Recall）三方面来分析算法的聚类质量：Ac⁃curacy（AC），Precision（PE），Recal1（RE）分别定义如下：

式中：n表示数据集的对象数；ai表示正确分到第i类的对象数；bi表示误分到第i类的对象数；ci表示应该分到第i类却没分到的对象数；k表示聚类个数。从UCI数据集中挑选了2组数据Mushroom和Breast Cancer，Mushroom数据集有一列属性中包括不确定属性，因此，这里分两种情况处理，即移除该属性列和将不确定属性值用特定属性值取代。3组数据描述如表2所示。

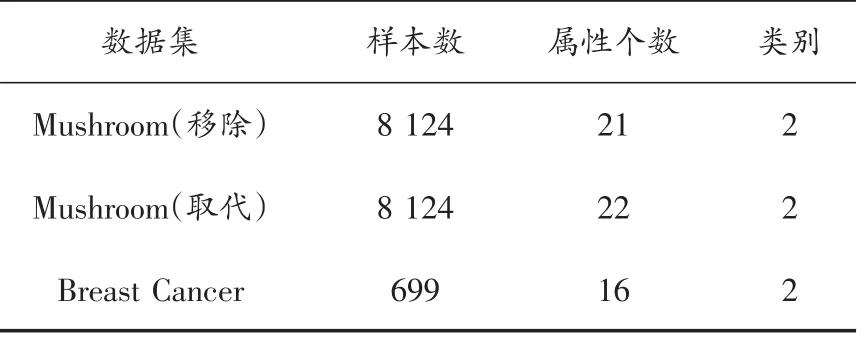
表2 数据集描述

表3～表5是改进的K⁃Modes算法和Huang的K⁃Modes聚类算法在3个数据集上的性能比较。

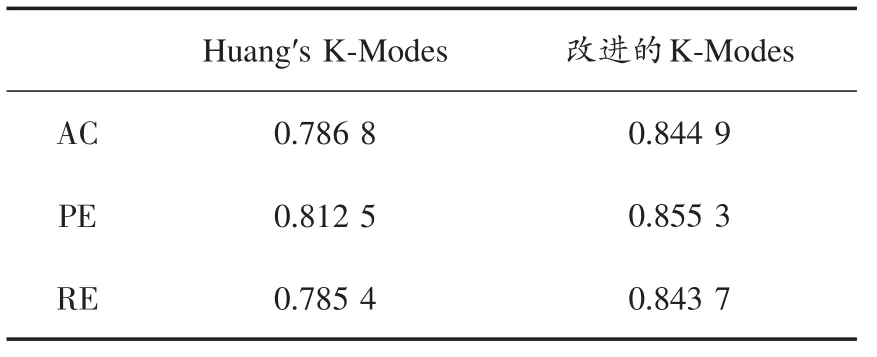
表3 在M ushroom（移除）数据集上算法的性能比较

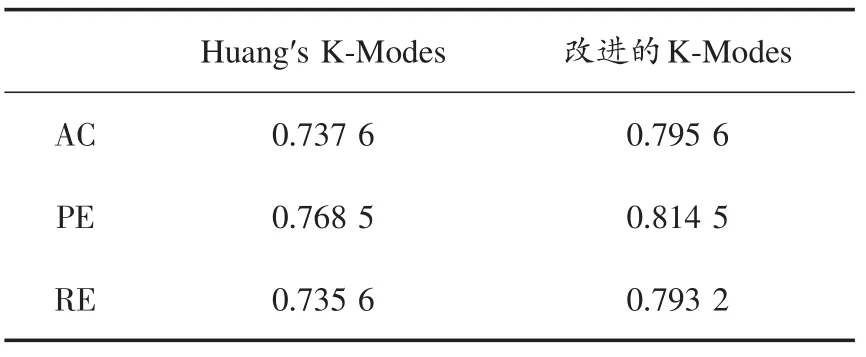
表4 在M ushroom（取代）数据集上算法的性能比较

表5 在Breast Cancer数据集上算法的性能比较

通过分析表3～表5，在数据Mushroom和Breast Can⁃cer上，改进的K⁃Modes聚类算法得到了较好的聚类效果，优于传统的K⁃Modes聚类算法。

4 结语

本文提出一种改进的K⁃Modes算法，首先采用简单匹配方法依次选取最不相同的k个类中心，其他数据采用期望熵较小的方法进行归类，并且定义了基于期望熵的目标函数。通过实验和传统的K⁃Modes算法进行比较，结果表明在相同的实验环境下，改进的K⁃Modes聚类算法在准确率、类精度和召回率上都优于传统的K⁃Modes聚类算法。

[1]CHEN M S，HAN J，YU P S.Datamining：an overview from a database perspective[J].IEEE Transactions on Knowledge and Data Engineering，1996，8（6）：866⁃883.

[2]JAIN A K，DUIN R P，MAO J.Statistical pattern recognition：a review.[J].IEEE Transactions on Pattern Analysis and Ma⁃chine Intelligence，2000，22（1）：4⁃37.

[3]BERKHIN P.Survey of clustering data mining techniques[R].San Jose，CA ：Accrue Software，2002.

[4]HUANG Zhe⁃xue.Extensions to the k⁃means algorithm for clustering large data sets with categorical values[C]//Pro⁃ceedings of Data Mining and Knowledge Discovery.Nether⁃lands：Kluwer Academic Publishers，1998：283⁃304.

[5]HAN Jia⁃wei，KAMBER M.Data mining concepts and tech⁃niques[M].San Francisco，USA：Morgan Kaufmann，2001.

[6]梁吉业，白亮，曹付元.基于新的距离度量的K⁃Modes聚类算法[J].计算机研究与发展，2010，47（10）：1749⁃1755.

[7]HE Zeng⁃you，DENG Sheng⁃chun，XU Xiao⁃fei.Improving K⁃modes algorithm considering frequencies of attribute values in mode[C]//Proceedings of the International Conference on Com⁃putational Intelligence and Security.Berlin：Springer⁃Verlag，2005：157⁃162.

[8]NG K N，LIM J，HUANG JZ，et a1.On the impact of dis⁃similarity measure in k⁃modes clustering algorithm[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2007，29（3）：503⁃507.

[9]CAO Fu⁃yuan，LIANG Ji⁃ye，LIDe⁃yu.A dissimilarity mea⁃sure for the k⁃Modes clustering algorithm[J].Knowledge⁃Based Systems，2012，26：120⁃127.

[10]BARBARA D，COUTO J，LIY.Coolcat：an entropy⁃based al⁃gorithm for categorical clustering[C]//Proceedings of ACM 11th International Conference on Information and Knowledge Management.[S.l.]：ACM，2002：582⁃289.