基于总体冲突概率和三维布朗运动的冲突探测算法

石 磊吴仁彪黄晓晓

①(中国民航大学智能信号与图像处理天津市重点实验室 天津 300300)

②(天津大学电子信息工程学院 天津 300072)

基于总体冲突概率和三维布朗运动的冲突探测算法

石 磊①②吴仁彪*①黄晓晓①

①(中国民航大学智能信号与图像处理天津市重点实验室 天津 300300)

②(天津大学电子信息工程学院 天津 300072)

随着空中交通流量的增加，冲突探测在空中交通管理系统中的作用越来越重要。该文提出了一种概率型冲突探测算法，计算向前看时间内的总体冲突概率。基于飞机3维布朗运动模型，飞机的预测航迹可以表示为确定航迹外加布朗运动扰动。对于两飞机速度为常值的运动情况，冲突概率可以表示为做布朗运动的飞机进入运动的飞机保护区的概率，使用坐标变换和Bachelier-Levy定理进行估计；对于两飞机运动为非匀速运动情况，预测航迹则可以使用足够多速度为分段常值的片段来近似，计算出每一片段内的冲突概率，并给出了向前看时间内总体冲突概率的上下界。与蒙特卡罗仿真结果比较，算法满足冲突探测精度要求，对及时发现冲突和冲突解决具有重要意义。

空中交通管理系统；总体冲突概率；3维布朗运动；坐标变换；Bachelier-Levy定理

1 引言

空中交通管理的基本要求是保证飞行的安全。空域中飞行的安全是以飞机之间发生冲突的次数来衡量的。当飞机之间的距离小于等于最小安全间隔时则认为发生飞行冲突[1]。最小安全间隔分为最小水平间隔和最小垂直间隔，它们构成了一个以飞机为中心的圆柱形保护区。航路区的最小水平间隔为9.3 km，终端区的最小水平间隔为5.6 km。在未实行缩小最小垂直间隔(RVSM)之前，飞机飞行高度在8.8 km以上时，最小垂直间隔为610 m，飞机飞行高度在8.8 km以下时，最小垂直间隔为305 m[2]；实行RVSM之后，最小垂直间隔标准均为305 m。

随着民用和通用航空运输业的快速发展，空域中飞行密度大大增加，如何高效地利用有限空域并保证飞行安全成了空中交通管理系统的一个巨大挑战。飞行冲突探测成为了空中交通管理系统保障飞行安全高效的一个重要工具。飞行冲突探测的基本思路就是利用雷达数据、ADS-B数据以及交通管制信息等，提前探测出可能的飞行冲突，并给予管制员提示，让管制员有足够的时间通知飞行员来避免飞行冲突的发生。

飞行冲突探测包括确定型冲突探测和概率型冲突探测[3]。确定型冲突探测根据飞机当前位置和速度不考虑其它因素的影响预测飞机未来航迹并进行冲突判断，而概率型冲突探测则考虑飞机受到导航、跟踪控制精度以及风等因素影响，预测航迹具有不确定性，从而导致冲突结果为概率。关于概率型冲突探测，国内外研究者进行了一系列的研究。Prandini等人[4,5]提出了计算飞行冲突概率的随机化方法；刘小龙等人[6]提出了一种改进的Prandini概率型冲突探测算法，提高了运算效率；梁海军等人[7]提出了3维坐标系下的冲突探测算法，使用蒙特卡罗方法计算冲突概率并分析了一系列参数对冲突概率的影响；文献[8]提出了基于位置空间离散化思想的快速算法来计算冲突概率；文献[9]提出了基于航迹预测的位置预测模型，使用概率分布函数估计法估计冲突概率。以上方法基于瞬时冲突概率，瞬时冲突概率反映了在某一时刻两飞机冲突的可能性，并不能直接代表一段时间内两飞机冲突的可能性，并且瞬时冲突概率对于两飞机预测航迹误差较为敏感，当预测航迹误差协方差很大时，冲突概率会变小，有可能导致漏警。而总体冲突概率则是向前看时间内两飞机冲突的概率，更能反映两飞机在向前看时间内冲突的可能性。文献[10]提出了自由飞行情况下飞机航迹预测模型，使用不同的概率密度描述飞机动态参数，并使用蒙特卡罗方法求解冲突概率；文献[11]使用多级分解以及序贯蒙特卡罗的方法计算冲突概率，来减小计算量。不过蒙特卡罗方法计算量依然较大，不太适合于工程应用。文献[2,12]提出了飞机位置预测误差模型以及一种估计方法求冲突概率，适用于航路上匀速飞行的飞机，但并不适合飞机飞行状态改变的情况。文献[5,13]提出了基于布朗运动的冲突探测算法，求向前看时间内的冲突概率；李丹等人[14]对基于布朗运动的方法进行改进用于减小误警率，不过文献[5,13,14]提出的冲突探测算法仅仅适用于2维空间两飞机匀速直线运动的情况，对于3维空间中飞机改变飞行方向等情况则不适用。

针对上述问题，本文提出了一种基于总体冲突概率思想的冲突探测算法，适用于3维空间中飞机运动不仅仅为匀速直线运动的情况，并提出了一种冲突概率的估计方法。飞机运动模型基于3维布朗运动，飞机冲突概率可以表示为做布朗运动的飞机进入运动的飞机保护区的概率。对于两飞机相对运动为匀速直线运动情况(相对速度为常值)，使用坐标变换和Bachelier-Levy定理来估算冲突概率。对于相对运动为非匀速直线运动的情况，则可以使用足够多相对速度为分段常值的片段来近似，求出每一片段的冲突概率，则向前看时间内总体冲突概率上下界可以由每个片段的冲突概率给出。

2 飞行冲突概率模型

2.1 飞机运动模型

本节建立飞机运动模型，预测在[0,T]时间段内的飞机航迹，其中T为向前看时间。建立以xyz为坐标轴的惯性坐标系，其中xy为水平面坐标轴，z为垂直方向坐标轴。

飞机在飞行中会受到风等一系列不确定因素的影响。这些因素对飞机地面速度dX(t)/dt 的扰动可以认为呈高斯分布[5,13]，即

其中()tX和()tu为t时刻飞机的位置和空速，()tω为高斯分布的随机变量。考虑飞机在3维空间中飞行，t时刻飞行方向在水平面的投影与惯性坐标系x轴正向夹角为()tθ，则飞机位置()tX可以用随机微分方程表示。

其中B(t)为标准布朗运动；Σ=diag(σa,σc,σv)，其中,,分别是飞机水平航向、水平侧向和垂直方向速度扰动的功率谱密度。R(θ(t))为t时刻的旋转矩阵，由于风对飞机水平速度和垂直速度影响可以认为是独立的，因此R(θ(t))为[12]

2.2 飞机速度为常值时的冲突概率

不妨考虑飞机A和B，其中飞机A在0t=时刻位于惯性坐标系原点，飞机B在=0t时刻位于0Δx。飞机A速度为Au，速度矢量在水平面投影平行于x轴正向；飞机B速度为Bu，速度矢量在水平面投影与x轴正向夹角为θ，则两飞机位置()AtX和()BtX可以表示为

其中()AtB和()BtB分别为标准布朗运动，2Σ为飞机速度扰动的功率谱密度，()θR为飞机B的旋转矩阵。

两飞机相对位置()tΔX可以由式(4)可得

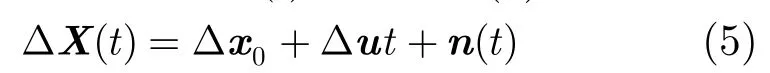
其中ΔX(t)=XB(t)-XA(t), Δu=uB-uA, n(t )=R(θ)ΣBB(t)-ΣBA(t )。

假设两飞机在向前看时间[0,]T内发生冲突的事件为(0,)TC，则

其中A

D是由最小安全间隔构成的以飞机A为中心的圆柱形保护区，保护区半径为r，高度为h。

两飞机冲突概率CP为事件(0,)TC发生的概率，即

2.3 飞机速度为分段常值函数时的冲突概率

对于飞机进行转弯等非匀速直线运动，可以使用足够数量的匀速直线运动片段来近似，即速度为分段常值函数。假设飞机A和B速度矢量为uA(t)和uB(t)，两飞机位置XA(t)和XB(t)可以使用随机微分方程来表示。

两飞机相对位置ΔX(t )可以由式(8)得到。

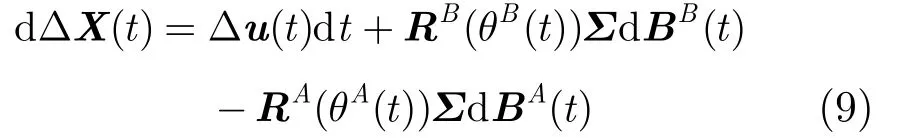
其中ΔX(t)=XB(t)-XA(t ),Δu(t)=uB(t)-uA(t )。

由于飞机A和B的速度为分段常值函数，因此将两飞机各段速度的起始和终点时刻TiA和TjB按照从小到大进行排序可得Tk，其中0≤k≤l,l为合并后速度片段的个数。则

其中T0=0并且Tl=T,Δuk为[Tk,Tk+1)时间段的相对速度矢量，为常值矢量。

假设在t∈[Tk,Tk+1)时间段内，两飞机发生冲突的事件为C(Tk,Tk+1)，则

假设两飞机在向前看时间[0,]T内发生冲突的事件为(0,)TC，则

因此，两飞机冲突概率CP可以定义为

为了表述方便，令Ck=C(Tk,Tk+1)。由概率论基本知识可得

对于两飞机相对飞行路线分为多个片段的情况，一般在两飞机飞行路线交叉的时间片段内冲突概率最大，并且其它时间片段内飞行冲突概率很小，因此可以使用两飞机飞行路线交叉的时间片段内的总体冲突概率来衡量两飞机在向前看时间内的冲突可能性，即PC≈max(P(Ci))。

3 冲突概率估计算法

3.1 飞机速度为常值时冲突概率的估计

由式(5)可知飞机A在原点做随机运动n(t)，飞机B以Δx0为起点做速度为Δu的运动。两飞机冲突概率则可以看作在原点做随机运动的飞机A进入运动的飞机B保护区的概率，假设飞机B运动着的保护区为，则两飞机冲突概率为

对于式(15)可以使用蒙特卡罗方法进行计算，但计算量很大，这里给出一种方法估计PC的值[15]。

(1)非正交变换 由于n(t)=R(θ)ΣBB(t) -ΣBA(t)，并且假定BA(t)和BB(t)是不相关的，随机运动n(t)的协方差为

随机运动n(t)可以通过非正交变换矩阵L-1变为标准的布朗运动(t)，即

由式(16)和式(17)可得

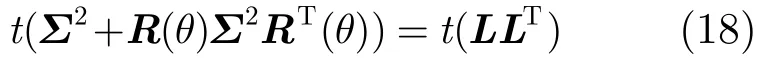
矩阵L的具体计算见文献[15]。

式(5)两边乘以矩阵1-L得

将随机运动n(t)变换为标准布朗运动n(t)后，进行正交变换使得相对速度v的方向与坐标系某一个坐标轴平行。

(2)正交变换 建立以z1z2z3为坐标轴的惯性坐标系，其中z1z2轴组成水平面，z3轴垂直于水平面向上。为了便于计算冲突概率，需要正交变换将相对速度矢量v=[v,v,v]T旋转到与z坐标轴平行。

1231其中正交变换包括水平旋转和垂直旋转，具体计算见文献[15]。

假设水平旋转和垂直旋转的矩阵分别为R1和 R2，则经过两次旋转变换，式(19)变为

其中z(t)=R2R1ΔZ(t ), a=R2R1Δz0,ω=R2R1v ，标准布朗运动(t)对于旋转变换R2R1是不变的。

(3)冲突概率的估计 令Mt为飞机B经过非正交和正交变换后的保护区。由式(20)可知，变换后的保护区是以a为起点，速度为ω进行匀速运动的一个椭圆柱体，如图1所示。

图1 经过非正交和正交变换后的保护区

此时两飞机冲突概率CP表达式变为

冲突概率PC可以看作一个在原点开始的标准布朗运动(t)进入一个初始位置在a速度为ω的运动椭圆柱保护区的概率。

在图1中，pt是经过保护区Mt的中心且垂直于相对速度ω的平面。是保护区Mt在pt平面的投影，为不规则的形状，St是边长分别平行于z2和z3轴的包含的最小矩形，如图2所示。其中Δz2和Δz3分别是St两边边长的一半。

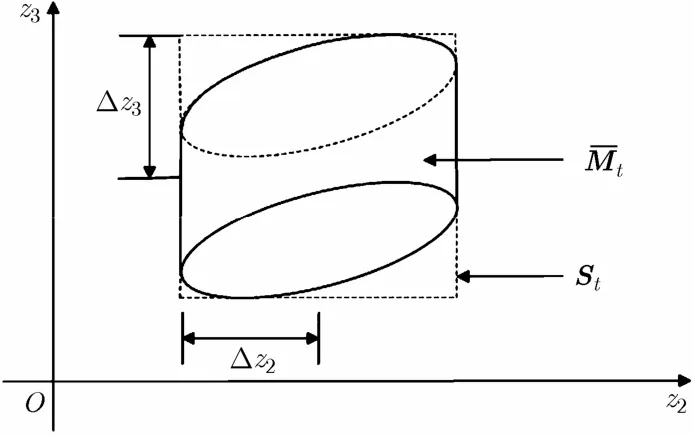
图2 非正交和正交变换后的保护区在tp平面的投影

针对式(21)中PC的计算，本文提出了一种估计方法。当标准布朗运动n(t)首次击中运动着的平面pt，其落在矩形St内的概率是对PC很好的估计。

令初始位置a的坐标值为(a1,a2,a3)T，速度ω大小为ω，则基于Bachelier-Levy定理，n(t)首次击中运动着的平面pt的概率密度函数为

那么冲突概率CP的估计表达式为

其中P(z(τ)∈St|τ=t )是t时刻布朗运动n(t)击中平面pt时候在矩形St内的概率。当τ=t时刻，标准布朗运动(t)在平面pt内呈2维高斯分布，其均值是0，方差为tI2。则P(z(τ)∈St|τ=t)可以表示为

其中

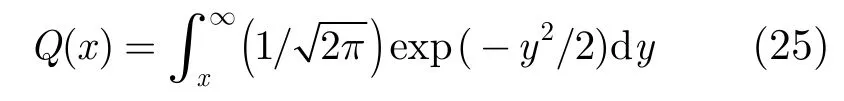
有关2zΔ和3zΔ的计算见文献[15]。

首中时间τ的均值为

由于首中时间τ的概率密度集中于t0:=E[τ]附近，因此对P(z(τ)∈St|τ=t)在t0处进行0阶泰勒展开，即可获得很高的估计精度[16]，则得

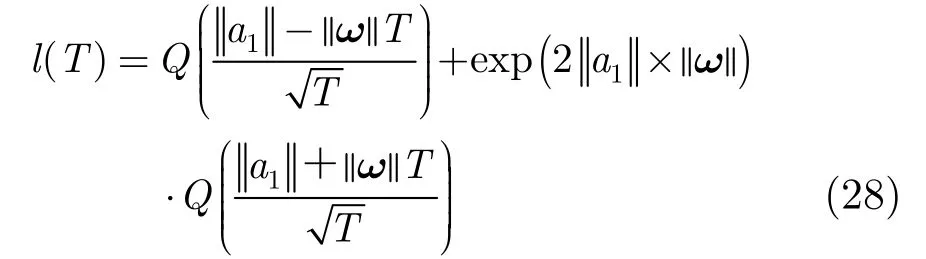
其中()Qx见式(25)。

由式(27)和式(28)可得

3.2 两飞机速度为分段常值函数情况下冲突概率的估计

计算两飞机在速度为分段常值情况下的冲突概率，需要计算冲突事件C(Tk,Tk+1)的概率。由式(11)可知，事件C(Tk,Tk+1)表示在t∈[Tk,Tk+1)时间段内，两飞机相对位置在飞机A保护区DA内的事件。

由式(2)可知，在Tk时刻两飞机相对位置服从高斯分布，假设均值为Δxk，协方差为ΣTk，如图3所示。我们将相对位置Δxk以t∈[Tk,Tk+1)时间段内的速度Δuk按照时间向前线性逆推到0时刻得Δ。起始位置为Δ的布朗运动在T时刻的位置k服从均值为Δx协方差为的高斯分布。相对速

图3 相对飞行速度为两段情况下两飞机相遇几何

k度Δuk与前一段的相对速度Δuk-1速度方向改变不大时，协方差和相差不大，并且对于求t∈[Tk,Tk+1)一段时间内的冲突概率来说，Tk时刻相对位置协方差对求[Tk,Tk+1)时间段内总体冲突概率影响并不大，影响其概率的是两飞机在[Tk,Tk+1)时间段内的最小距离以及到达最小距离的时刻。

因此求P(C(Tk,Tk+1))可以使用式(23)，不过对时间的积分上下限需要变为Tk+1和Tk，即

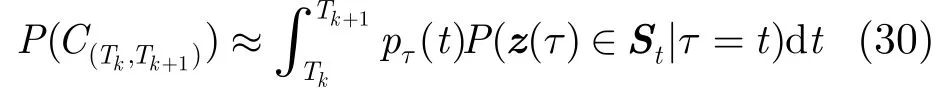
由式(27)和式(29)得

由式(31)和式(14)可以求出向前看时间段[0,]T内冲突概率CP的上限值和下限值。

4 仿真与分析

4.1 飞机速度为常值情况下的仿真

设置向前看时间为10 min，圆柱形保护区半径为5.6 km，高度为610 m。考虑两架飞机A和B，其中飞机A初始位置为坐标系原点，速度A=u (123.5,0,0)Tm/s，飞机B的初始位置为Δ，速度为uB，其水平速度大小为154.3 m/s，垂直速度为7.6 m/s，飞机B水平速度方向与坐标系x轴正向夹角为θ。如图4所示。

图4 两飞机相遇几何

改变0Δx和θ值，使得两飞机最小距离、到达最小距离时刻以及水平面上相遇角度不同，在这些情况下，本文算法求出的冲突概率与蒙特卡罗仿真结果的误差如表1所示。

其中使用蒙特卡罗仿真次数105次。本文计算结果平均绝对误差小于0.01，最大绝对误差为0.042，满足冲突探测对精度的要求[2]。最大绝对误差出现在两飞机水平速度夹角较小并且两飞机最小距离是保护区半径5.6 km时，原因是飞行速度夹角较小时，两飞机位置的布朗运动相关性大，而本文忽略两飞机位置布朗运动的相关性。

4.2 飞机速度为分段常值情况下的仿真

设置向前看时间为10 min，圆柱形保护区半径为5.6 km，高度为610 m。考虑两架飞机A和B在同一水平面内飞行，其中飞机A初始位置为坐标系原点，速度Au大小为123.5 m/s，速度方向与x轴正向夹角为60°，预计飞行3 min后，速度大小不变，但速度方向与x轴正向夹角变为30°。飞机B的初始位置为(35.7,0,T0)km，飞行速度Bu大小为123.5 m/s，速度方向与x轴正向夹角为132°，预计两飞机在第4 min到达最小距离且最小距离为0。这里设置飞机B在第2 min进行水平协调转弯改变飞行速度方向，转弯率为2.5/s°，其中可以进行右转弯或者左转弯，转过一定角度后继续直线飞行，如图5所示。

表1 本文结果与蒙特卡罗仿真结果的误差

图5 两飞机相遇几何

本文分别仿真飞机B向左或者向右转弯角度为5°至50°的情况。本文中将转弯分为两个直线片段来近似，则这种情况下两飞机相对飞行路线可以分为5段，分别是0时刻至飞机B开始转弯的时间片段([0,2] min)，转弯2个时间片段，转弯后至飞机A改变飞行速度方向的时间片段以及飞机A改变飞行速度方向后至向前看时间的片段([3,10] min)。

前4个时间片段，两飞机最近距离远大于5.6 km，求出的两飞机冲突概率为0。在[3,10] min片段内，也即两飞机飞行路线交叉片段，两飞机最近距离随着转弯角度的变大而从0变大。两飞机飞行路线交叉时间段[3,10] min内的冲突概率本文算法和蒙特卡罗仿真结果如图6所示。

其中使用蒙特卡罗仿真次数为510次，本文结果与蒙特卡罗仿真结果最大绝对误差为0.034。平均绝对误差小于0.01。当飞机B向左或者向右转弯40°时，两飞机预计最小距离为7.6 km和8.5 km，两飞机冲突概率均小于0.05，则一定程度上可以认为没有冲突。

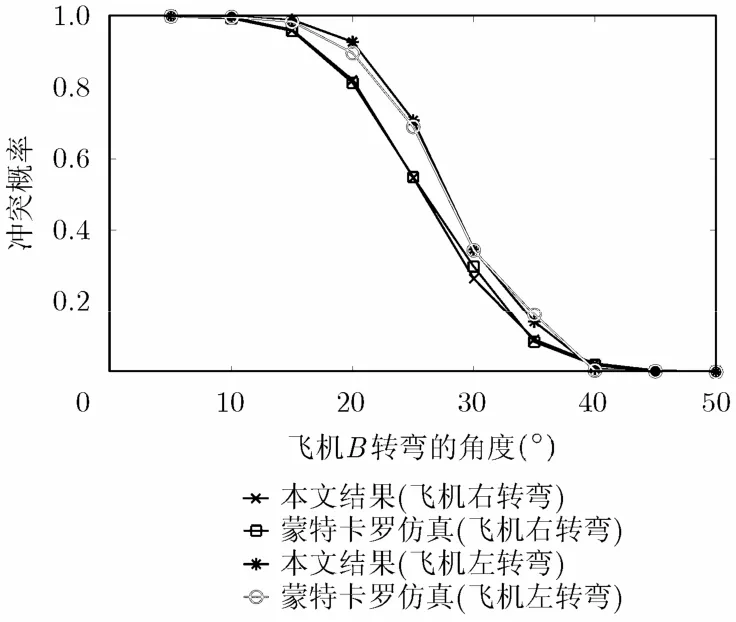
图6 飞行路线交叉片段的冲突概率

5 结论

本文根据飞机布朗运动模型和总体冲突概率思想提出了一种适用于3维空间中飞机运动不仅仅为匀速直线运动情况下的冲突探测算法。对于飞机速度为常值情况，使用坐标变换和Bachelier-Levy定理来估算冲突概率。对于飞机速度是分段常值情况，求出了每个时间片段内的冲突概率并给出了向前看时间内冲突概率的上下限。仿真结果验证了本文算法的精度满足冲突探测精度的要求，对空中交通管理系统发现冲突以及进行冲突解决有重要意义。

[1] Federal Aviation Administration. Aeronautical information manual-official guide to basic flight information and ATC procedures[R]. Washington, D.C., 2012.

[2] Paielli R A and Erzberger H. Conflict probability estimation for free flight[J]. Journal of Guidance, Control and Dynamics, 1997, 20(3): 588-596.

[3] Kuchar J and Yang L. A review of conflict detection and resolution modeling methods[J]. IEEE Transactions on Intelligent Transportation Systems, 2000, 1(4): 179-189.

[4] Prandini M, Lygeros J, Nilim A, et al.. Randomized algorithms for probabilistic aircraft conflict detection[C]. Proceedings of the 38th IEEE Conference on Decision and Control, Berkeley, CA, USA, 1999, 3: 2444-2449.

[5] Prandini M, Hu J, Lygeros J, et al.. A probabilistic approach to aircraft conflict detection[J]. IEEE Transactions on Intelligent Transportation Systems, 2000, 1(4): 199-220.

[6] 刘小龙, 罗以宁, 赵喜求, 等. 一种改进的Prandini概率型中期冲突探测方法[J]. 计算机技术与发展, 2013, 23(1): 214-216. Liu Xiao-long, Luo Yi-ning, Zhao Xi-qiu, et al.. An improved medium-term conflict detection methods of Prandini probability type[J]. Computer Technology and Development, 2013, 23(1): 214-216.

[7] 梁海军, 杨红雨, 肖朝, 等. 3维坐标系下的飞行冲突探测算法[J]. 四川大学学报(工程科学版), 2013, 45(2): 88-93. Liang Hai-jun, Yang Hong-yu, Xiao Chao, et al.. Flight conflict detection algorithm based on the three dimensional coordinate system[J]. Journal of Sichuan University (Engineering Science Edition), 2013, 45(2): 88-93.

[8] 石磊, 吴仁彪. 预测位置空间离散化的多航路中期冲突探测算法[J]. 信号处理, 2012, 28(11): 1521-1528. Shi Lei and Wu Ren-biao. Multi-route mid-term conflict detection algorithm based on discretization of predicted position space[J]. Signal Processing, 2012, 28(11): 1521-1528.

[9] Liu W and Hwang I. Probabilistic trajectory prediction andconflict detection for air traffic control[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(6): 1779-1789.

[10] Yang L and Kuchar J. Prototype conflict alerting system for free flight[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(4): 768-773.

[11] Prandini M and Watkins O. Probabilistic Aircraft Conflict Detection[R]. Distributed Control and Stochastic Analysis of Hybrid Systems Supporting Safety Critical Real-Time Systems Design (HYBRIDGE), 2005.

[12] Paielli R and Erzberger H. Conflict probability estimation generalized to non-level flight[J]. Air Traffic Control Quarterly, 1999, 7(3): 1-12.

[13] Hu J, Lygeros J, Prandini M, et al.. Aircraft conflict prediction and resolution using Brownian motion[C]. Proceedings of the 38th International Conference on Decision and Control, Berkeley, CA, USA, 1999: 2438-2443.

[14] 李丹, 崔德光. 基于布朗运动的空中交通短期冲突探测[J]. 清华大学学报(自然科学版), 2008, 48(4): 477-481. Li Dan and Cui De-guang. Air traffic control conflict detection algorithm based on Brownian motion[J]. Journal of Tsinghua University (Science & Technology), 2008, 48(4): 477-481.

[15] Shi Lei and Wu Ren-biao. A probabilistic conflict detection algorithm in terminal area based on three-dimensional Brownian motion[C]. Proceedings of the 11th International Conference on Signal Processing, Beijing, 2012: 2287-2291.

[16] Hu J. A study of conflict detection and resolution in free flight[D]. [Master dissertation], Berkeley: University of California, 1999.

石 磊： 男，1985年生，博士生，研究方向为飞行冲突探测等.

吴仁彪： 男，1966年生，教授，研究方向为自适应信号处理及其应用等.

黄晓晓： 女，1989年生，硕士生，研究方向为飞行冲突探测等.

Conflict Detection Algorithm Based on Overall Conflict Probability and Three Dimensional Brownian Motion

Shi Lei①②Wu Ren-biao①Huang Xiao-xiao①

①(Tianjin Key Laboratory for Advanced Signal Processing, Civil Aviation University of China, Tianjin 300300, China)
②(School of Electronic Information Engineering, Tianjin University, Tianjin 300072, China)

With the increasing of the air traffic flow, conflict detection plays an increasingly important role in air traffic management system. A probabilistic conflict detection algorithm is proposed. Overall conflict probability in look-ahead time is calculated. The aircraft predicted trajectory is expressed as deterministic trajectory plus a Brownian motion perturbation. For the case of constant aircraft speed, conflict probability is expressed as the probability of an aircraft with Brownian motion perturbation entering a time-varying moving protection zone, the probability is approximated using coordinate transformation and Bachelier-Levy theorem. For the case of aircraft with non-constant speed, predicted trajectory can be approximated by a large enough number of constant speed segments. Conflict probability of each segment is calculated and the overall conflict probability bounds in look-ahead time are given. Compared with Monte Carlo simulations, the proposed algorithm is accurate for conflict detection and it is useful to detect and avoid conflicts in air traffic management system.

Air traffic management system; Overall conflict probability; Three dimensional Brownian motion; Coordinate transformation; Bachelier-Levy theorem

TP391

A

1009-5896(2015)02-0360-07

10.11999/JEIT140363

2014-03-19收到，2014-09-17改回

国家科技支撑计划(2011BAH24B12)和国家自然科学基金委员会与中国民航局联合资助项目(U1233109)资助课题

*通信作者：吴仁彪 rbwu@cauc.edu.cn