基于复数因子分析模型的步进频数据压缩感知

徐丹蕾 杜 兰刘宏伟 王鹏辉 丛玉来

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

基于复数因子分析模型的步进频数据压缩感知

徐丹蕾 杜 兰*刘宏伟 王鹏辉 丛玉来

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

认知雷达发射高距离分辨率步进频信号通常需要较长的观测时间。为了节省时间资源，该文提出一种贝叶斯重构算法，用较少的步进频信号脉冲得到的频点缺失频域数据，重构出相应的全带宽频域数据。首先利用复数贝塔过程因子分析(Complex Beta Process Factor Analysis, CBPFA)模型对一组全带宽频域数据进行统计建模，求解得到其概率密度函数；然后在目标被跟踪且姿态变化不大的情况下，只发射步进频信号的部分脉冲，根据先前CBPFA模型得到的概率密度函数，对频点缺失的频域数据利用压缩感知理论和贝叶斯准则解析地重构出相应的全带宽频域数据。基于实测1维高分辨距离(High Range Resolution, HRR)数据的重构实验，证明了该文提出方法的性能。

认知雷达；步进频；贝叶斯重构算法；压缩感知；因子分析模型

1 引言

增加雷达发射信号的带宽可以提高雷达距离分辨率，从而获得更多目标信息，但瞬时带宽的增加必将提升对硬件的要求，在现有硬件条件下调频步进信号是一种工程实用、方便灵活的高距离分辨率形式[1]。调频步进波形是一组载频以固定频率增量变化的窄带脉冲串，每个脉冲调制为线性调频。利用带宽信号合成技术[1]，可以将调频步进信号中各个子脉冲的子带宽组合成一个大的全带宽信号，从而实现距离维的高分辨率。

尽管调频步进信号可以实现距离维的高分辨率，但步进调频雷达是以时间资源换取系统带宽，有观测时间长的缺点[2]。现代雷达通常多功能多模式协同工作，不仅发射高分辨宽带信号，还要完成搜索、跟踪等重要工作。实际中，雷达一般交替发射宽窄带信号，在利用窄带进行跟踪或扫描时停止发射宽带信号，因此对目标的宽带观测时间非常有限且不连续[2]。因此考虑只发射调频步进信号的部分脉冲，得到频点缺失的频域回波数据，然后利用得到的频点缺失频域数据恢复出相应的全带宽的频域数据，即能减少宽带观测时间。

压缩感知(Compressive Sensing, CS)[3-5]理论指出当对信号用远低于奈奎斯特采样定理要求的速率采样时，它仍能实现准确的信号重构。∈CL×1表示未知信号，则信号采样模型可以表示为：y= Φx +，其中y∈CJ×1表示观测信号，∈CJ×L是观测矩阵，J≪L,ξ∈CJ×1表示噪声。CS理论表示如果信号x能够稀疏地用某些字典Q∈CL×E表示，也即x=Qg,g∈CE×1表示稀疏的系数，那么它就能高概率地被准确地重构出来。在传统的CS稀疏编码过程中，字典Q通常是固定和给定的。利用CS理论可以很容易解决上述频点缺失频域数据重构问题，在该问题中，y表示已知的频点缺失频域数据，x表示待重构的全带宽频域数据，即为从x中抽取部分元素的抽取矩阵[6]。

本文提出了一种不同于传统CS的重构算法，主要应用于认知雷达(cognitive radar)[7,8]。认知雷达是近几年提出的一种全新的信号处理系统，如今已成为雷达技术领域的一个研究热点，它具备对环境和目标信息的在线感知和记忆能力，结合先验知识，可以实时优化雷达发射和接收处理模式，达到和目标及环境的最优匹配，获得更好的目标探测性能。本文针对跟踪到的目标，首先发射一组完整的调频步进信号，得到该目标的一组全带宽的频域数据，并用于学习；然后利用能自动学出因子个数的CBPFA模型对其进行统计建模，并计算相应的概率密度函数，作为反馈信息；接着在目标姿态变化不大的情况下，进行发射信号调整(即只发射调频步进信号的部分脉冲)，得到频点缺失频域数据；最后利用反馈的全带宽频域数据概率密度函数，结合压缩感知理论和贝叶斯准则，对频点缺失频域数据进行解析的重构，得到全带宽的频域数据，实现节省时间资源的目的。与只能利用固定字典和观测样本潜在稀疏性进行重构的传统CS算法相比，本文提出的统计压缩感知算法不仅能自动学习字典，而且利用了一组全带宽频域数据作为先验知识，因此能得到更好的重构效果。

2 全带宽频域数据的CBPFA(Complex Beta Process Factor Analysis)模型

2.1 调频步进信号分析

当发射调频步进信号[1]时，假设合成后全带宽信号载频为fc，带宽为Bp，调频率为γ，脉冲长度为Tp，子脉冲信号带宽为BM，脉冲长度为TM，频率步长为fs，步数为M，则子脉冲载频为

脉冲串的第m个子脉冲的发射信号为

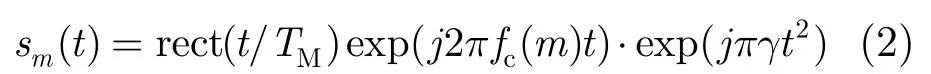
对单点目标，信号回波为

其中τ=2R/c表示目标回波的时间延迟，R为目标距雷达的距离，c为光速。与回波信号混频的参考信号为sref_m(t)=exp(j2πfc(m)t)，混频后：

对sm(t)进行脉冲压缩，得到脉冲压缩后频域信号：

带宽合成技术是调频步进信号的一个重要技术，它是将多个频率步进的窄脉冲信号通过一定算法，使其等效为一个大带宽信号，以获得高距离分辨率的处理技术，例如常用的频域拼接合成技术[1]，即将子脉冲频谱sm(f)在频域频移，叠加为一个大带宽信号，从而得到一个全带宽频域数据x=(f-(m-1/2-M/2)f)，拼接后的信号总 s带宽为Bp=MBM。

2.2 全带宽频域数据的CBPFA模型

认知雷达先发射一组完整的调频步进信号，得到一组全带宽的频域数据X=，用作先验知识，其中第n个样本为xn=[xn1,xn2,…,xnL]T, L为样本维度。通常可近似认为步进频回波数据服从复高斯分布[9]，因此采用因子分析(Factor Analysis, FA)模型对这组全带宽的频域数据进行建模。传统FA模型需要事先确定因子个数，但如果因子个数设置过大，则会导致过匹配，若设置过小，则不能充分描述数据的统计分布。因此，本文在传统因子分析模型的基础上加入了能根据数据自动学习因子个数的Beta-Benoulli先验[1012]-。另外，在雷达数据中，回波的相位信息对于成像或识别等应用都有很重要的意义[13]，但是传统因子分析模型只能描述实数据，在对雷达数据建模过程中丢掉了相位信息。基于此，本文提出一种非参数贝叶斯结构(即CBPFA)去完成复数全带宽频域数据的统计建模。第n个全带宽频域数据可以表示为

其中A=[A1,A2,…,AK]∈CL×K表示这一组全带宽频域数据的共享因子加载矩阵；K为预设的因子个数；εn︵=[,εn2,…,εnL]T∈CL×1表示噪声变量；=[,,…,]T∈CK×1表示稀疏权值，它由两部分组成：权值w=[w,w,…,w]T和二进制

nn1n2nK分配变量zn=[zn1,zn2,…,znK]T，其中wn只表示的权重，没有稀疏信息，而二进制变量zn∈{0,1}则用来实现稀疏，只在对应于A的一部分列向量的位置上非0，符号⊙表示两个向量的点乘。

本文假设噪声εn服从均值为零，方差为τ-1IL的复高斯分布，即

其中CN()·表示复高斯分布。

文献[10-12]为参数nw加上一个零均值的复高斯先验分布：

其中超参数α用来控制nw的分布。为了规范层次化的先验，需要对权重和噪声的精确度(α和τ)分别定义超先验[1012]-，合适的先验分布为Gamma分布：)

其中()Γ·为Gamma函数，0a,0b,0c和0d为Gamma分布的参数。

对于因子加载矩阵A，对它的每一列定义零均值的复高斯先验：

对二进制变量nz，为了让它实现稀疏，这里使用Bernoulli-Beta先验，它是Beta过程的一个有限近似[1012]-：

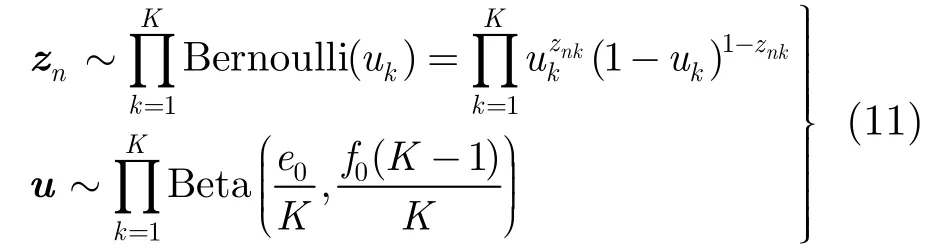
其中Bernoulli()·和Beta()·分别表示伯努利分布和贝塔分布。通常设置K为一个比较大的数，因此ku的期望，，近似为0，也即意味着p(znk=1)非常小，实现了zn的稀疏(大部分元素为0)。当zn中某些元素为0时，A中相应的列和wn中相应的元素就会为0，也即实现了因子个数的自动选择。

为了更形象描述CBPFA模型，图1给出它的有向无环图。

2.3 变分贝叶斯(Variational Bayes, VB)推导

为了满足准确性和有效性的折中，本文采用VB[14]方法推导CBPFA模型。

在给定观测数据D和超参数θ的情况下，贝叶斯推导力图估计出隐变量Ψ的后验分布：

图1 有向无环图表示一组全带宽频域数据的CBPFA模型

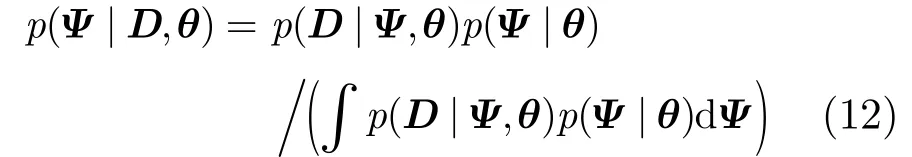
其中ΚL(q(Ψ)|p(Ψ|D,θ))是q(Ψ)和p(Ψ|D,θ)之间的Kullback-Leibler距离。因为KL(q(Ψ)|p(Ψ|D, θ))≥0，也即L(q(Ψ))是lnp(D|θ)的一个严格下界。因此通过最小化ΚL(q(Ψ)|p(Ψ|D,θ))，就能得到q(Ψf)的最优参数估计结果。

2.4 全带宽频域数据的概率密度估计

对CBPFA模型进行VB推导后，下面利用隐变量的后验分布求解这一组全带宽频域数据的概率密度函数：

表1 基于VB推导的CBPFA

因为wn的后验分布为q(wn)=CN(μn,Σn)，因此的后验均值和协方差可以表示为

通常可以近似认为一组全带宽频域数据的均值近似为零[13]，而且实测数据的实验结果也符合该结论，因此，这里为了简化模型，设定服从零均值的复高斯分布，即

把式(17)代入式(14)，再利用共轭特性，就能得到该组全带宽频域数据的概率密度函数：

3 频点缺失频域数据的压缩感知重构

在被跟踪目标姿态变化不大(如目标回波中散射点不发生严重越距离单元走动[9])的情况下，只发射调频步进信号的部分脉冲，得到频点缺失的频域数据y*，假设它对应的全带宽频域数据为x*，则y*=Φx*+ξ*。下面介绍如何从y*中解析地重构出相应的x*。

假定噪声ξ*服从均值为零，协方差为B-1IJ的复高斯，因此p(y*|x*)=CN(y*;Φx*,B-1IJ)。根据贝叶斯准则，y*给定情况下x*的条件分布[11]为

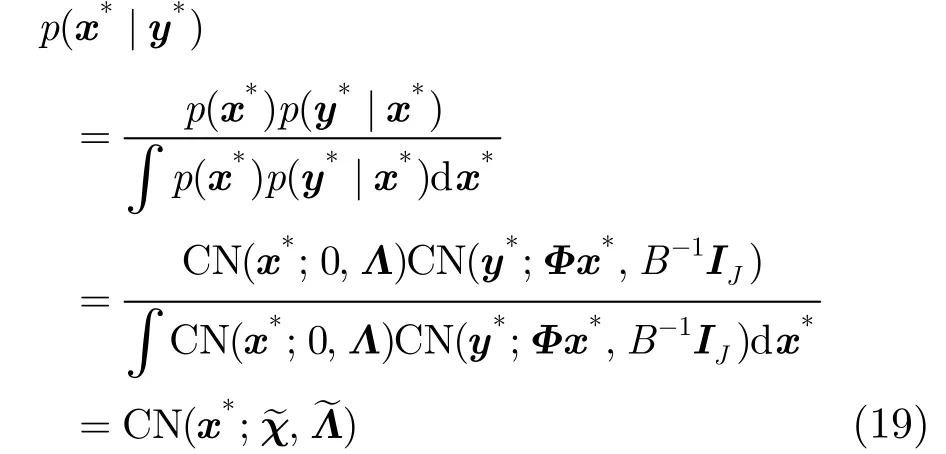
其中

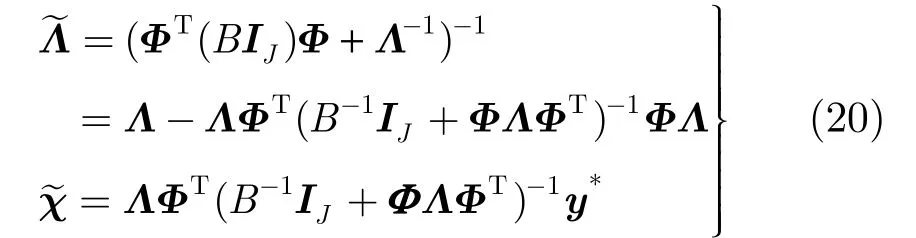
式(19)中用CN(x*;0,Λ)代替p(x*)，也即认为x*与之前的一组全带宽频域数据服从同样的统计特性，这也就是为什么一直强调在目标姿态变化不大的情况下调整发射信号，得到频点缺失频域数据。在后面的实验部分，主要考虑B-1趋于0的情况，也即认为观测到的频点缺失频域数据y*是无噪的。

从式(20)中可以看到，求解p(x*|y*)需要的所有参数，都可以从p(x)的先验学习中得到，因此就可以解析地重构出频点缺失频域数据相应的全带宽频域数据。另外，通过贝叶斯模型得到的是p(x*|y*)的全概率模型，而不仅仅是对x*的点估计。在实际的操作中，可以把p(x*|y*)的均值χ~当作重构的全带宽频域数据x*。

4 实验结果分析

由于本文算法直接应用于步进频合成后的频域数据，并不需要考虑步进频合成的过程，因此，我们在实验中直接使用国内某研究所的逆合成孔径C波段雷达测量飞机数据[9,15]，该数据每个HRR样本包含256个频点，也即L=256。

4.1 全带宽频域数据的学习结果分析

这里设定用作先验知识的全带宽HRR频域数据的个数为N=1024。在对该组全带宽的HRR频域数据进行CBPFA建模前，首先需要对HRR数据进行敏感性处理[9]。图2给出了其中一组全带宽HRR频域数据的因子选择结果，也即的学习情况。从图2中可以看到，这一组全带宽HRR频域数据学出的因子个数要明显小于我们预设的因子个数K=100，证明了CBPFA模型能实现自动确定因子个数。

4.2 随机抽取的频点缺失频域数据的CS重构结果分析

下面通过实验来验证本文方法对频点缺失HRR频域数据的重构效果。均匀地从所有样本中选取1500个HRR频域数据作为实验对象，遍历所有目标和方位，待重构样本的前面1024个全带宽HRR频域数据作为它们的先验知识。本文采用相对重构误差，也即来量化重构的性能，其中I=1500表示待重构样本的个数，∈CJ×1表示第i个待重构的频点缺失HPP频域数据，表示对应的真实全带宽HRR频域数据，表示在给定观测数据y的情况下重构的第i个全带宽HRR频域数据的条件期望。

在引言中已经讲到设置观测矩阵Φ为抽取矩阵，因此本节采用最常用的随机抽取方式[6,12]重点讨论观测样本维度J对重构效果的影响。设定J的大小从50到140，间隔为10，则它们相对于全带宽HRR频域数据维度256L=的比例/JL分别为：0.20, 0.23, 0.27, 0.31, 0.35, 0.39, 0.43, 0.47, 0.51和0.55。

与本文方法比较的有正交匹配追踪(Orthogonal Matching Pursuit, OMP)[5]和贝叶斯压缩感知(Bayesian Compressive Sensing, BCS)[16]两种传统CS方法。对于这两种CS方法，它们需要预先知道字典Q。根据HRR的散射点特性，选择Q为超完备傅里叶基[2]，相应的维度为800 E=。

图3给出了随着观测样本维度的变化，3种重构方法对这1500个频点缺失HRR频域数据的相对重构误差的变化比较。从图3中可以看出本文方法的重构性能要明显好于BCS和OMP，这表明了本文方法利用全带宽的HRP频域数据作为先验信息，以及贝叶斯自动学习字典的有效性，同时BCS的重构效果好于OMP，也验证了贝叶斯方法的优越性。另外，从图中可以看出，随着观测样本维度的增加，3种方法的相对重构误差都趋于变小，表明了在一定程度上观测样本维度越高，重构效果越好。

图4给出了一些HRR频域数据重构的例子。为了同时验证本文方法对HRR频域数据幅度和相位的重构性能，这里把重构的HRR频域数据进行逆快速傅里叶变换(Inverse Fast Fourier transform, IFFT)，得到时域实数的1维高分辨距离像(High Range Resolution Profile, HRRP)。这里给出图3中10个例子的其中2个：抽取比例/JL为0.27和0.47。另外，针对每一个抽取比例，均给出一个时域HRRP例子。图4中，图4(a), 4(c), 4(e)为抽取比例0.27时，本文方法、OMP和BCS对同一个样本在时域的重构结果以及它们各自的相对重构误差，图4(b), 4(d), 4(f)为抽取比例0.47时，3种比较方法对另一个样本在时域的重构结果以及它们各自的相对重构误差。从图4中可以看出，抽取比例为0.27时，3种方法相对重构误差分别为0.1536, 0.3295, 0.2155，抽取比例为0.47时，3种方法相对重构误差分别为0.1668, 0.2673, 0.2232。可见，不管抽取比例为0.27或0.47，本文方法的重构效果都要好于OMP和BCS，本文方法把HRRP散射点的细节基本都重构出来了，而通过OMP重构的样本有许多虚假点，BCS重构出的样本准确度要低于本文方法。因此本文方法具有很好的重构效果。

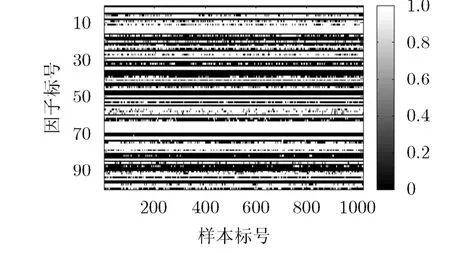
图2 一组全带宽HRR频域数据的因子选择结果

图3 观测样本维度(抽取比例) 与相对重构误差的关系

图4 当抽取比例分别为0.27和0.47时，本文方法、OMP和BCS对复HRR频域样本重构后的时域实数HRRP样本示例

5 结束语

本文提出了一种利用全带宽的频域数据作为先验知识，然后再利用压缩感知理论和贝叶斯准则，对频点缺失的频域数据解析地重构出相应的全带宽频域数据的方法。通过实测HRR数据对比了本文方法和传统的CS方法，证明了本文方法重构的有效性。另外，实验部分只给出了最常见的随机抽取方式，但是如何抽取才能以最少的观测样本得到最好的重构效果是现在研究的热点和难点，因此下一步的工作就是定性分析各种抽取方式的优劣。

[1] 高昭昭. 高分辨ISAR成像新技术研究[D]. [博士论文], 西安电子科技大学, 2009. Gao Z Z. New technologies of high resolution ISAR imaging [D]. [Ph.D. dissertation], Xidian University, 2009.

[2] Zhang L, Qiao Z J, Xing M D, et al.. High-resolution ISAR imaging with sparse stepped-frequency waveforms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4630-4635.

[3] Candes E J, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[4] 马坚伟, 徐杰, 等. 压缩感知及其应用: 从稀疏约束到低秩约束优化[J]. 信号处理, 2012, 28(5): 609-623. Ma J W, Xu J, et al.. Compressive sensing and its application: from sparse to low-rank regularized optimization[J]. Signal Processing, 2012, 28(5): 609-623.

[5] Tropp J A and Wright S J. Computational methods for sparse solution of linear inverse problems[J]. Proceedings of the IEEE, Special Issue on Applications of Compressive Sensing & Sparse Representation, 2010, 98(6): 948-958.

[6] Hu L, Shi Z G, Zhou J X, et al.. Compressed sensing of complex sinusoids: an approach based on dictionary refinement[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3809-3822.

[7] Chavali P and Nehorai A. Scheduling and power allocation in a cognitive radar network for multiple-target tracking[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 715-729.

[8] 黎湘, 范梅梅. 认知雷达及其关键技术研究进展[J]. 电子学报, 2012, 40(9): 1863-1870. Li X and Fan M M. Research advance on cognitive radar and its key technology[J]. Acta Electronica Sinica, 2012, 40(9): 1863-1870.

[9] Du L, Liu H W, Bao Z, et al.. A two-distribution compounded statistical model for radar HRRP target recognition[J]. IEEE Transactions on Signal Processing, 2006, 54(6): 2226-2238.

[10] Paisley J and Carin L. Nonparametric factor analysis withBeta process priors[C]. International Conference on Machine Leaning (ICML), 2009: 777-784.

[11] Chen M, Silva J, Paisley J, et al.. Compressive sensing on manifolds using a nonparametric mixture of factor analyzers: algorithm and performance bounds[J]. IEEE Transactions on Signal Processing, 2010, 58(12): 6140-6155.

[12] Zhou M, Chen H, Paisley J, et al.. Nonparametric Bayesian dictionary learning for analysis of noisy and incomplete images[J]. IEEE Transactions on Image Processing, 2012, 21(1): 130-144.

[13] 王鹏辉. 基于统计建模的雷达高分辨距离像目标识别方法研究[D]. [博士论文], 西安电子科技大学, 2012. Wang P H. Study of radar high resolution range profile target recognition based on statistical modeling[D]. [Ph.D. dissertation], Xidian University, 2012.

[14] Beal M J. Variational algorithms for approximate Bayesian inference[D]. [Ph.D. dissertation], University of London, 2003.

[15] Du L, Liu H W, Wang P H, et al.. Noise robust radar HRRP target recognition based on multitask factor analysis with small training data size[J] IEEE Transactions on Signal Processing, 2012, 60(7): 3546-3559.

[16] Ji S H, Xue Y, and Carin L. Bayesian compressive sensing[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2346-2356.

徐丹蕾： 女，1985年生，博士生，主要研究方向为雷达目标识别、机器学习、统计信号处理.

杜 兰： 女，1980年生，教授，博士生导师，主要研究方向为统计信号处理、雷达信号处理、机器学习及其在雷达目标检测与识别方面的应用.

刘宏伟： 男，1971年生，教授，博士生导师，主要研究方向为雷达信号处理、MIMO雷达、雷达目标识别.

王鹏辉： 男，1984年生，讲师，主要研究方向为统计机器学习理论、基于一维高分辨距离像的雷达自动目标识别.

丛玉来： 男，1988年生，博士生，主要研究方向为雷达信号处理、雷达参数估计.

Compressive Sensing Using Complex Factor Analysis for Stepped-frequency Data

Xu Dan-lei Du Lan Liu Hong-wei Wang Peng-hui Cong Yu-lai
(National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China)

It usually takes a long observing time when a cognitive radar transmits the High-Range-Resolution (HRR) stepped-frequency signal. To save time, partial pulses of the stepped-frequency signal are transmitted to obtain the incomplete frequency data, and a Bayesian reconstruction algorithm is proposed to reconstruct the corresponding full-band frequency data. Firstly, the Complex Beta Process Factor Analysis (CBPFA) model is utilized to statistically model a set of full-band frequency data, whose probability density function (pdf) can be learned from this CBPFA model. Secondly, when the target is tracked and its attitude changes not much, the cognitive radar can just transmit the partial pulses of the stepped-frequency signal, and the corresponding full-band frequency data can be analytically reconstructed from the incomplete frequency data via the Compressive Sensing (CS) method and Bayesian criterion based on the previous pdf learned with CBPFA model. The reconstruction experiments of the measured HRR data demonstrate the performance of the proposed method.

Cognitive radar; Stepped-frequency; Bayesian reconstruction algorithm; Compressive Sensing (CS); Factor analysis model

TN958

A

1009-5896(2015)02-0315-07

10.11999/JEIT140407

2014-03-27收到，2014-08-29改回

国家自然科学基金(61271024, 61201296, 61322103)和全国优秀博士学位论文作者专项资金(FANEDD-201156)资助课题

*通信作者：杜兰 dulan@mail.xidian.edu.cn