几种常用扩频序列的性能分析及仿真
2015-07-18张莉
张 莉
(南京航空航天大学 金城学院, 江苏 南京 211156)
几种常用扩频序列的性能分析及仿真
张 莉
(南京航空航天大学 金城学院, 江苏 南京 211156)
扩频码对扩频通信的性能起着重要作用,一般用计算机实现扩频码的设计与性能仿真.利用Matlab工具编制了m序列、Gold序列和Kasami序列的生成程序及自相关、互相关函数的计算程序.程序简单,只需输入线性移位寄存器的反馈系数,即可输出相应的扩频码,进而得出扩频码的相关性、平衡性等性能指标.
扩频通信; 扩频码; m序列; Gold序列; Kasami序列; 仿真
0 引言
扩频通信与常规通信的根本区别是信息在发送之前进行了频谱扩展.频谱扩展是通过高速的扩频码与低速的信息码直接相乘实现的.扩频通信具有信号频谱宽、波形复杂、安全隐蔽等显著特点,大大增加了对信号进行截获、检测、测向定位和干扰的难度. 扩频码对扩频通信的性能具有决定性的重要作用,抗干扰、抗噪声、抗截获、信息数据隐蔽和保密、抗衰落、多址通信、实现同步与捕获等都是与扩频码的设计密切相关的.
扩频通信对扩频码的要求是:
1)具有尖锐的自相关函数,而互相关函数应接近于零;
2)有足够长的码周期,以确保抗侦破、抗干扰的要求;
3)序列平衡性好;
4)工程上易于产生、加工、复制和控制.
扩频码选用伪码(PN码)用于扩展频谱通信.所谓伪码,即伪随机编码,也称伪随机序列、伪噪声码,是由近似随机出现的、有一定规律并可复制的、1和0数目大致相等的序列组成.
在扩频系统中,对伪随机序列而言,最关心的问题就是其相关特性,包括自相关性及互相关性.下面给出这些相关函数的定义.
设有两条长为N的序列{a}和{b},序列中的元素分别为ai,bi,(i=1,2,3,…,N).则序列的自相关函数定义为:
(1)
序列{a}和{b}的互相关函数定义为
(2)
1 常用伪码相关性的仿真分析
本文主要讨论由线性移位寄存器产生的线性移位寄存器序列,包括m序列、Gold序列和Kasami序列.
1.1 m序列的相关性仿真分析
如果一个n级线性移位寄存器产生的序列的周期P=2n-1,那么该序列就叫做最长线性移位寄存器序列,简称m序列.
m序列的平衡性较好,在每个周期内,0比1少出现次数少一次.根据式1,可推出其自相关函数为
这个公式说明,m序列具有双值自相关函数特性.下面给出了6级m序列a的自相关函数的Matlab仿真图(图1),为了更好的说明m序列的自相关特性,图中绘出了m序列2个周期的自相关函数.

图1 6级m序列a的自相关函数
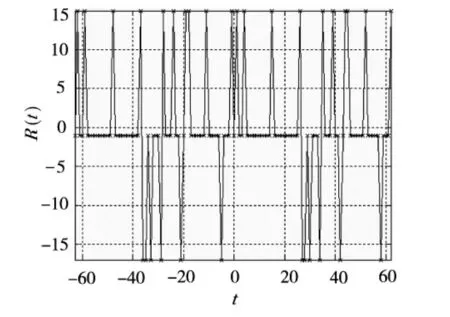
图2 6级m序列a和b的互相关函数
由图1可以看出,m序列的自相关函数呈三角形.具有这种自相关函数的伪码,在通信和测距系统中是很有用的.例如,只要有两个通信系统的码序列相移在1个bit以内时,则它们就可以同时工作,这就能够实现同一发射频域内的多址通信.在测距系统中,利用相关峰值作为测量标记,可以保证距离测量精确到1bit之内.在测量中,只要调整相关检测器,使它在±1bit检测电平之间识别,而对其他的较低和较高的电平不识别,就能达到测量高度精确的目的.
但是m序列(周期相同)之间的互相关性不够理想,当作为扩频码使用时,会增大多址干扰.图2是由Matlab程序产生的6级的m序列a和b的互相关函数图像.从图2中可以看出,它们的互相关函数值包括3个:{-1,-17,15},并且-1所占的比例很小,这样能组成互相关函数值小的m序列集的数量很少,无法满足多用户的需求.
1.2 Gold序列的相关性仿真分析

图3 Gold序列生成器
Gold序列是m序列的组合序列,由同步时钟控制的一对m优选对逐位模2加得到,Gold序列的周期为P=2n+1.其产生模型如图3所示.
Gold序列虽然是由一对m序列模2加得到的,但它已经不是m序列了,不过仍然具有与m序列近似的相关特性,各个序列之间的互相关特性与原来两个m序列之间的互相关特性一样,最大的互相关值不会超过原来的两个m序列最大互相关值.Gold序列的特性主要有以下三点:
1)周期为P=2n+1,具有比m序列大得多的独立码组.
2)一周期内任意一对序列的互相关函数值都是三值的,其可能值为{-1,-t(n),t(n)-2},其中t(n)如下式:
3)Gold序列的每个码组的自相关函数也从集合{-1,-t(n),t(n)-2}中取值,因此自相关函数的峰值以t(n)为上界.
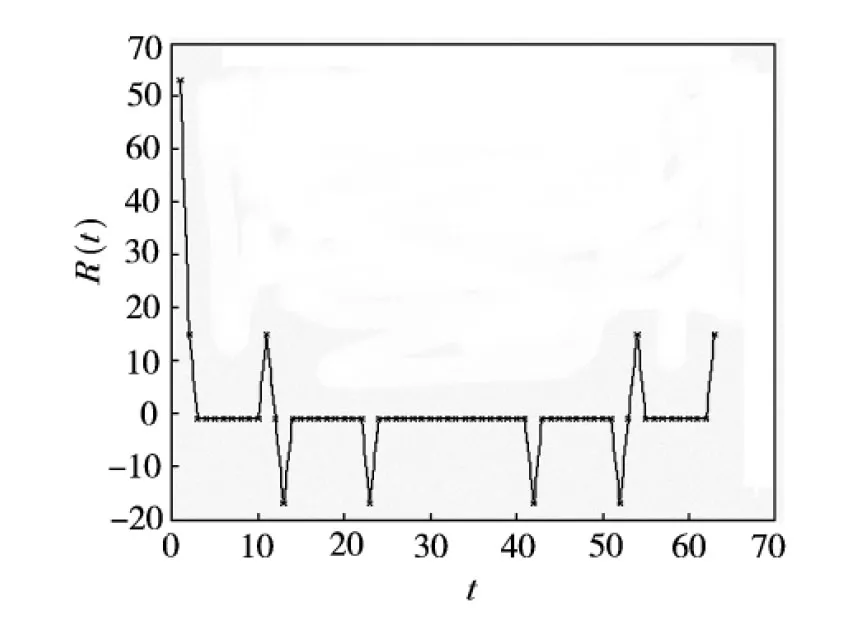
图4 6级Gold序列a的自相关函数

图5 6级Gold序列a和b的互相关函数
Gold序列虽然具有平衡性良好、序列数量较多、自相关特性良好,但其互相关特性与m序列类似,即互相关值小的Gold序列集合较少.
1.3 Kasami序列的相关性仿真分析
Kasami序列与Gold序列类似,也是一种在m序列基础上构造出来的扩频序列.它继承了m序列的良好的随机特性,同时又具有自、互相关特性均较好的的特点,且数量也很可观.Kasami序列有大小两类,前者序列数较多,后者较少.Kasami序列的相关性能比较好,其中Kasami小集合序列的相关性能比Kasami大集合序列还要好.限于篇幅,本文只讨论Kasami小集合序列的的相关性.
Kasami小集合序列的自相关函数和互相关函数值都在下列集合中:{-1,-s(n)),s(n)-2}(其中s(n)=1+2n/2).当n=6时,s(n)=9,因此其自相关函数和互相关函数的取值范围是{-9,-1,7},图6和图7是由Matlab程序产生的6级的Kasami小集合序列的自相关函数和互相关函数图像.

图6 6级Kasami序列a的自相关函数
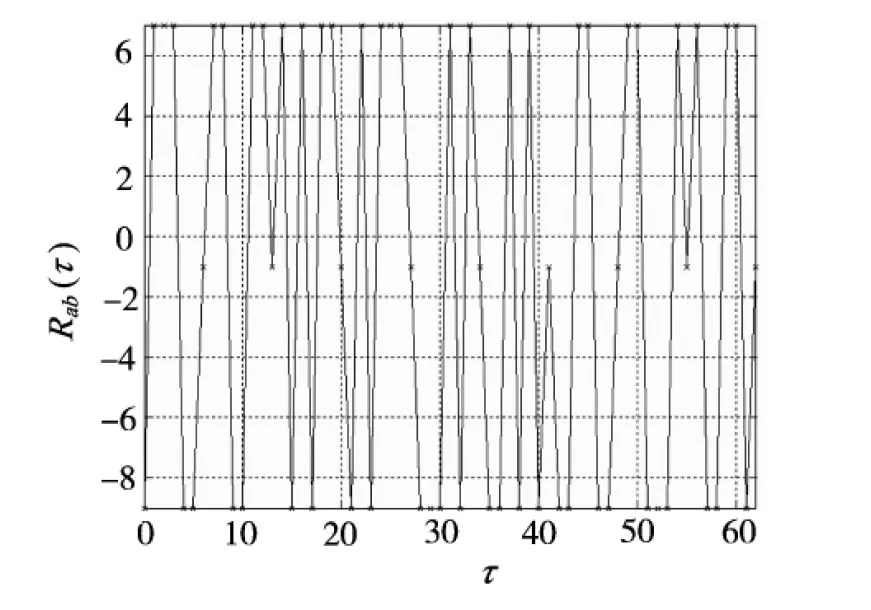
图7 6级Kasami序列a和b的互相关函数
由图6和图7可以看出,Kasami小集合序列的互相关峰值较前两者小,互相关特性更为优良.
2 结论
本文从扩频通信中对扩频码的基本要求入手,讨论了扩频码中常用的m序列、Gold序列和Kasami序列,并用Matlab对以上序列的相关性进行了仿真.本文内容对工程技术人员具有较强的参考价值,对开展相关领域研究也具有一定的借鉴意义.
[1]霍姆斯J K.相干扩展频谱系统[M].北京:国防工业出版社,1991.
[2]李承恕,赵荣黎.扩展频谱通信[M]. 北京:人民邮电出版社,1993.
[3]张冬辰,周吉.军事通信[M]. 北京:国防工业出版社,2008.
[4]张志涌,徐彦琴.Matlab教程[M]. 北京:北京航空航天大学出版社,2001.
[5]王会华,李宝平.m序列发生器的设计与实现[J].北京电子科技学院学报,2007,15(2):58-62.
[6]张莉.Kasami序列的产生与性能分析[D]. 南京:南京航空航天大学,2007.
[责任编辑:蒋海龙]
AnalysisandSimulationofSevralSpreadSpectrumCodes
ZHANG Li
(Jincheng College, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu 211156, Chian)
Spread spectrum codes play an important role in spread spectrum system.In this paper,we use MATLAB to generate some common spread spectrum codes and analyse their auto correlation and cross correlation,such as M sequences, Gold sequences and Kasami sequences.
spread spectrum; spread spectrum codes; m sequence; gold sequence; kasami sequence; simulation
2014-12-24
张莉(1982-),女,江苏沛县人,讲师,硕士,研究方向为车载通信等.E-mail: kasami11@163.com
TN79
: A
: 1671-6876(2015)02-0130-04
