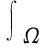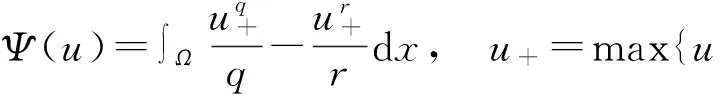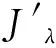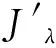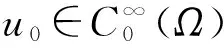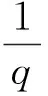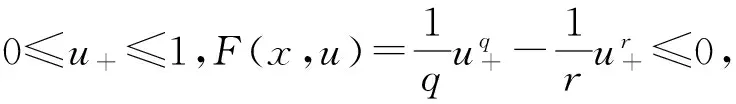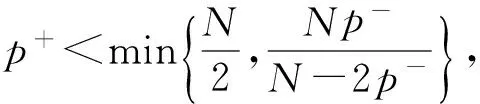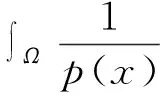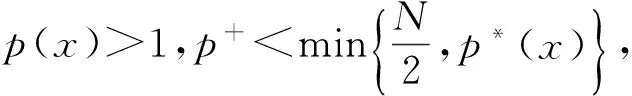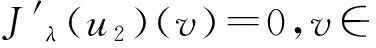带p(x)-双调和算子的四阶椭圆型问题的多解性
2015-07-18缪清
缪 清
(云南民族大学 数学与计算机科学学院, 云南 昆明 650500)
带p(x)-双调和算子的四阶椭圆型问题的多解性
缪 清
(云南民族大学 数学与计算机科学学院, 云南 昆明 650500)
利用极值原理结合山路定理研究了一类带Navier边值条件的四阶椭圆型问题至少存在两个非负、非平凡的弱解.
p(x)-双调和算子; Navier边值条件; 多解性; 山路定理
0 引言
令Ω为RN(N≥1)中的具有光滑边界的有界子集,本文讨论了一类p(x)-双调和方程的多解性,
(1)
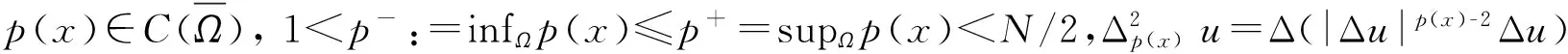
近年来,双调和问题的解的存在性和多解性引起了许多学者的兴趣[1-4]. 由于p(x)-双调和算子是非齐次的,因此很多适用于p-双调和算子的方法则不能直接应用于p(x)-双调和算子.Yin[1]利用Ricceri’s三临界点定理,推广了Li[2]的结果,研究了p(x)-双调和问题
的多解性.Li[3]利用了等价的Ricceri’s三临界点定理,研究了问题带Navier边值条件的p(x)-双调和问题的多解性.Kong[4]应用临界点定理研究当非线性项f(x,u)为b(x)|u|γ(x)-2u-c(x)|u|β(x)-2u时p(x)-双调和问题非平凡解的存在性.Amrouss[5]应用了Ricceri变分原理研究了不同边值条件下p(x)-双调和问题的多解性.
本文我们主要考虑问题(1)中当非线性项为
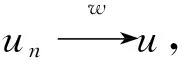
时,其中1 令 当空间Lp(x)(Ω)赋予如下范数时 则(Lp(x)(Ω),|·|p(x))为Banach空间,称之为广义的Lebesgue空间.定义空间Wm,p(x)(Ω), Wm,p(x)(Ω)={u∈Lp(x)(Ω)|Dαu∈Lp(x)(Ω),|α|≤m}, 范数‖u‖a,‖u‖,|Δu|p(x).在X中是等价的[7].为表述方便,记X中的范数为‖u‖a. (c)‖u‖a→0⟺ρ(u)→0. 定义1u∈X称为问题(1)的弱解如果对任意的v∈X满足 定义函数Jλ:X→R为 Jλ(u)=Φ(u)-λΨ(u), 其中 则函数Jλ∈C1(X,R),且有 因此,Jλ的临界点为问题(1)的弱解.如果u∈X为Jλ的临界点,则有 因此可以得到u≥0. 引理1[4]存在常数λ1>0,使得 引理2 函数Jλ是强制的,且有下界. 证明因为1 则对任意的λ>0,存在常数Cλ使得 其中λ1在引理1中给出,因此,对所有的‖u‖>1,有 因此Jλ是强制的,且有下界. 由引理2可知,存在u1∈X为函数Jλ的全局最小值.接下来的结果将说明当λ>0充分大时,u1≠0. 引理3 存在λ*>0,当λ≥λ*时有infu∈XJλ(u)<0. 证明令Ω0为Ω的一个紧子集,且|Ω0|>0.选取实数t0>1使得 由于 因此,存在充分大的λ*>0,使得对任意的λ∈[λ*,∞),有Jλ(u0)<0.进而当λ≥λ*充分大时,有Jλ(u1)<0,u1为问题(1)非负、非平凡弱解. 接下来将证明当λ>λ*时,函数Jλ满足山路定理的几何结构,问题存在第二个弱解u2∈X. 引理4 存在ρ∈(0,‖u1‖a),常数γ>0,使得u∈X,‖u‖a=ρ有Jλ(u)≥γ. 因此可得 因为1 引理5 函数Jλ满(PS)条件. 证明令um⊂X使得 (2) 其中X*为X的对偶空间.因为函数Jλ是强制的,由式(2)可知,{um}是有界的.因此存在一个子列记为{um}弱收敛到u∈X,因此{um}在Lq(Ω),Lr(Ω)中强收敛到u∈X. 由Holder不等式,可得 另一方面,由式(2)可知 (4) 由式(2)~(4)可知 limm→∞Φ′(um)(um-u)=0 (5) 由于{um}弱收敛到u∈X,则有 limm→∞Φ′(u)(um-u)=0 (6) 由式(5)和式(6),可知 limm→∞(Φ′(um)-Φ′(u))(um-u)=0. 因为Φ′:X→X′为型,则可得{um}强收敛到u∈X.因此函数Jλ满足(PS)条件. 证明由引理2和引理3,问题存在一个非负非平凡的弱解u1.记 其中 L:={l∈C([0,1],X):l(0)=0,l(1)=u1}, [1]Yin H, M Xu. Existence of three solutions for a Navier boundary value problem involving thep(x)-biharmonic opera-tor[J]. Ann Polo Math,2013,109(1): 47-58. [2]Li C, Tang C L. Three solutions for a Navier boundary value problem involving thep-biharmonic[J]. Nonlinear Anal, 2010,72(3-4): 1339-1347. [3]Li L, Ding L, Pan W W. Existence of multiple solutions for ap(x)-biharmonic equation. Electronic Journal of Diff Equat, 2013,139:1-10. [4]Kong L. On a fourth order elliptic problem with ap(x)-biharmonic operator[J]. Applied Math Letters, 2014,27:21-25. [5]Amrouss A R EI, Ourraoui A. Existence of solutions for a boundary problem involvingp(x)-biharmonic operator[J].Bol Soc Paran Mat,2013, 31(1):179-192. [6]Fan X L, Zhao D. On the spacesLp(x)(Ω)andW1,p(x)(Ω)[J]. Math Anal Appl 2001, 263(2): 424-446. [7]Zang A, Fu Y. Interpolation inequalities for derivatives in variable exponent Lebesgue-Sobolev spaces[J]. Nonlinear Anal, 2008, 69(10):3629-3636. [8]Ambrosetti A, Rabinowitz P H. Dual variational methods in critical points theorey and applications[J].J Funct Anal,1973, 14(4):349-381. [责任编辑:李春红] MultipleSolutionsforaFourthOrderEllipticProblemwithap(x)-BiharmonicOperator MIAO Qing (School of Mathematics and Computer Science, Yunnan Minzu University, Kunming Yunnan 650500, China) Using the minimum principle combined with the mountain pass theorem, wo obtain at least two non-negative,non-trivial weak solutions to a fourth order elliptic problem with ap(x)-biharmonic operator and the Navier boundary conditions. p(x)-biharmonic; navier boundary condition; multiple solutions; mountain pass theorem 2015-01-24 国家自然科学基金资助项目(11461083); 云南省应用基础研究资助项目(2013FD031) 缪清(1984-),女,云南马龙人,讲师,博士,研究方向为偏微分方程及其应用. E-mail: miaoqing-0404@163.com O175.6 : A : 1671-6876(2015)02-0095-051 预备知识及引理
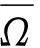
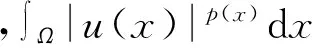
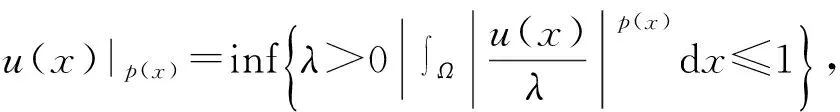
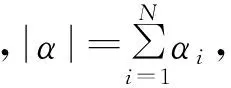
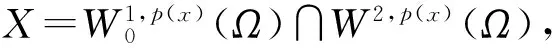
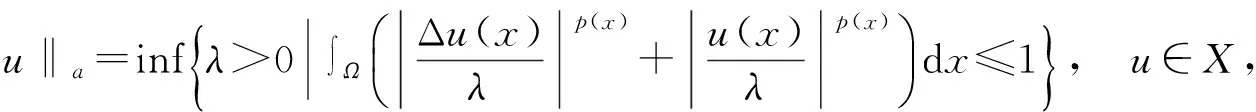
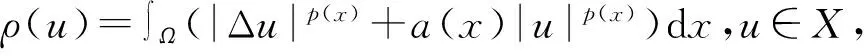
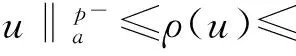
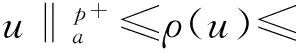
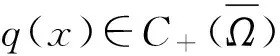
2 主要结果