二阶常微分方程Sturm-Liouville问题的正解的存在性
2015-07-18王伟
王 伟
(南京财经大学 应用数学学院,江苏 南京 210046)
二阶常微分方程Sturm-Liouville问题的正解的存在性
王 伟
(南京财经大学 应用数学学院,江苏 南京 210046)
运用Krasnoselskii不动点定理对二阶常微分方程Sturm-Liouville问题的正解存在性证明进行了推广.
微分方程; 边值问题; 正解; 不动点定理
0 引言
非线性常微分方程边值问题是微分方程研究中的一个重要的领域.1833~1841年间,Sturm和Liouville合作讨论了二阶线性齐次方程的边值问题和Sturm-Liouville特征值问题,他们将二阶线性微分方程化成
(p(t)x′)′+λq(t)x=0,p(t),q(t)>0,
它满足的边值条件为
x′(a)-αx(a)=x′(b)+βx(b)=0,α,β>0,
现在称为Sturm-Liouville边值条件,且得到了Sturm-Liouville特征值问题的一系列结果,形成了Sturm-Liouville理论.
马如云[1]研究了如下二阶边值问题
u"+f(t,u)=0,0 (1) αu(0)-βu′(0)=0,γu(1)+δu′(1)=0 (2) 在条件(i)f0=0且f∞=∞或,(ii)f0=∞且f∞=0,下的正解的存在性. 本文对其证明进行了推广,其中u(t)是问题(1)~(2)的正解是指当t∈(0,1)时,有u(t)>0,且u(t)满足微分方程(1)和边值条件(2). 且本文总假定: (A1)f∈C([0,∞),[0,∞)); (A2)α∈C([0,1],[0,∞))且在(0,1)内的任一子区间内α(t)不恒为0; (A3)α,β,γ,δ≥0及γβ+αγ+αδ>0 以下我们介绍本文所需要的一些概念及结果[2-3]. 定义1[2]我们称P是一个锥,如果P是E中某非空凸闭集,并且满足如下两个条件: (i)x∈p,λ≥0⟹λx∈p; (ii)x∈p,-x∈p⟹x=0. (B1)‖Au‖≤‖u‖,u∈K∩∂Ω1且‖Au‖≥‖u‖,u∈K∩∂Ω2或 引理2 (Arzela-Ascoli定理[3])设X是紧集,C(X)是X上连续函数形成的Banach空间,若Φ⊂C(X)是逐点有界且等度连续,即有 (C1)∀x∈X,sup{|f(x)|:∀f∈Φ}<∞; (C2)∀x∈X,∀ε>0,∃x的邻域V,使|f(y)-f(x)|<ε,∀y∈V及f∈Φ,则Φ在C(X)中完全有界. 定理1 设f(t,u)连续,u≥0,对t∈[0,1]有f(t,u)≥0,当u>0时f(t,u)在[0,1]的任意子区间上不恒为零,若α,β,σ≥0,及ρ=γβ+αγ+ασ>0且f满足: 则边值问题(1)~(2)至少存在一个正解. 当且仅当u是算子方程 的解.其中k(t,s)表示边值问题 u"=0, αu(0)-βu′(0)=0, γu(1)-σu′(1)=0, 的Green函数. 设K={u∈C[0,1]:u(t)≥0,minu(t)≥M‖u‖}是C[0,1]中的锥,其中 事实上,∀u,v∈k,λ∈(0,1),则 min(λu+(1-λ)v)≥λminu(t)+(1-λ)minv(t)=M‖λu‖+M‖(1-λ)v‖≥M‖λu+(1-λ)v‖, 即K为凸的. 则 若u∈k,-u∈k,则u(t)≥0,-u(t)≥0,即u(t)=0.由以上证明可知,K为C[0,1]中的锥. 记φ(t)=γ+σ-γt,ψ(t)=β+αt,0≤t≤1,则 所以 故 因此,若u∈K,则 所以,AK⊂K,显然A:k→k是全连续算子. 因此,若u∈K,则 (3) 所以 对∀ε>0,由K(t,s)在[0,1]×[0,1]中的一致连续性,∃σ使得对s∈[0,1]有 |k(t,s)-k(t′,s)|<ε(当|t-t′|<σ), 从而 (4) 因此,若u∈k,‖u‖=H1,则由式(3)和式(4)得 所以无论何种情况,只要令Ω2={u∈E,‖u‖ [1]马如云. 非线性常微分方程非局部问题[M]. 北京:科学出版社,2003. [2]孙经先. 非线性泛函分析及其应用[M]. 北京:科学出版社,2007:4-75 [3]张恭庆,林源渠. 泛函分析讲义:上册[M]. 北京:北京大学出版社,1987:206. [责任编辑:李春红] TheExistenceofPositiveSolutionsoftwoOrder WANG Wei (School of Applied Mathematics,Nanjing University of Finance and Economics,Nanjing Jiangsu 210046,China) This paper generalized the provement of the existence of positive solutions of two order Sturm-liouville boundary value problem by using Krasnoselskii fixed point theorem. differential equation; boundary value problem; positive solution; fixed point theorem 2015-04-02 王伟(1989-),女,河北邯郸人,硕士,研究方向为非线性分析及应用. E-mail:853529167@qq.com O175 :A :1671-6876(2015)03-0203-041 预备知识


2 主要结果及证明


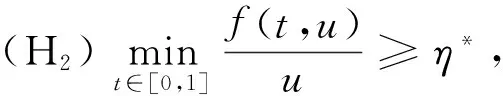




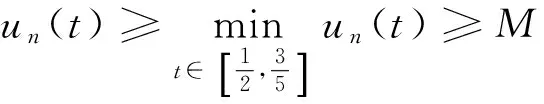




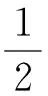









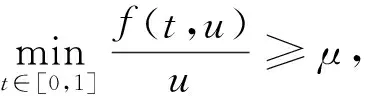



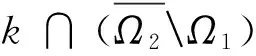
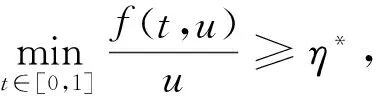



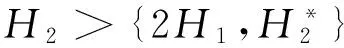

Sturm-LiouvilleBoundaryValueProblems
