混凝土裂缝非线性断裂的简化预测方法研究

卿龙邦，刘换换，罗丹旎，田稳苓

（1.河北工业大学土木工程学院，天津 300401；2.河北省土木工程技术研究中心，天津 300401；3.清华大学水沙科学与水利水电工程国家重点实验室，北京 100084）

混凝土裂缝非线性断裂的简化预测方法研究

卿龙邦1，2，刘换换1，罗丹旎3，田稳苓1，2

（1.河北工业大学土木工程学院，天津 300401；2.河北省土木工程技术研究中心，天津 300401；3.清华大学水沙科学与水利水电工程国家重点实验室，北京 100084）

混凝土的裂缝断裂问题是评定混凝土结构工程安全的关键问题．结合起裂韧度准则和黏聚力模型，提出了一种混凝土裂缝断裂分析的简化预测方法．通过给定裂缝黏聚力的分布形式，推导了裂缝张开位移、外荷载的表达式，结合拉伸软化曲线给出了相应的求解方程和求解步骤，获得了裂缝起裂至扩展的全过程曲线．其中，裂缝扩展基于起裂韧度准则，黏聚力产生的应力强度因子和位移采用权函数方法进行计算．利用不同尺寸的楔入劈拉试件对断裂全过程进行了计算，结合现有的混凝土断裂试验成果对本文方法进行了验证．结果表明采用本方法可完整的计算裂缝断裂全过程并准确的预测带裂缝构件的极限承载力，从而验证了本文方法的有效性和合理性．

混凝土；裂缝；断裂；起裂韧度；黏聚力

0 引言

混凝土的裂缝问题一直是土木、水利等行业科技界和工程界极为关心的热点问题．在实际结构安全分析中，模拟裂缝结构在外荷载作用下的断裂全过程对结构设计及安全校核起着至关重要的作用．混凝土裂缝前端存在断裂过程区，断裂过程区内发生微裂缝，集料互锁，粗糙表面的接触和摩擦等非线性现象，为能量耗散区．断裂过程区的存在是混凝土裂缝断裂呈现非线性的主要原因．自Kaplan[1]于1961年首次进行混凝土断裂试验以来，众多学者对混凝土断裂机理进行了研究，提出了大量的混凝土断裂模型和准则，而围绕这些断裂模型展开的分析方法研究也成为热门的课题．

基于有效裂缝概念的模型可采用简单的解析方法，如：Shah双参数模型[2]，Bazant尺寸效应模型[3]，Karihaloo有效裂缝模型[4]等．其中，Jenq和Shah[2]提出混凝土断裂双参数模型，采用临界应力强度因子判别裂缝断裂，同时引入另一个断裂参数，即临界裂缝尖端张开位移CTODc．Bazant[3]在钝裂缝带模型的基础上，从能量角度释放角度提出了准脆性材料结构破坏名义强度的尺寸效应公式，也称为Bazant尺寸效应律．Karihaloo等[4]基于等效裂缝的概念，提出采用有效裂缝模型来计算混凝土的断裂韧度．以上模型仅关注峰值荷载对应的裂缝断裂状态．Hillerborg等[5]提出虚拟裂缝模型，也称作黏聚裂缝模型，其思路与经典弹塑性断裂力学中Dugdale和Barenblatt分别提出的窄条塑性区模型相类似．虚拟裂缝模型将断裂过程区视为能传递应力的假想裂缝，该假想裂缝的尖端为未裂材料和损伤材料的分界点，假想裂缝的末端黏聚力为零，为真正裂缝的尖端，裂缝扩展的判据为裂缝尖端处的主拉应力等于材料的抗拉强度，裂缝沿与最大主拉应力垂直方向开裂，且黏聚力随裂缝张开位移的增大而减小．基于虚拟裂缝模型，采用有限元[5]、边界元[6]等方法能够模拟裂缝扩展过程．Bazant和Oh[7]提出的裂缝带模型将过程区等效为其有一定宽度的裂缝带，亦可模拟混凝土裂缝断裂的非线性过程．虚拟裂缝模型及裂缝带模型均利用拉伸软化曲线描述断裂过程区的软化特性．

然而，对于裂缝扩展而言，以上研究分别采用等效断裂韧度准则或强度扩展准则，而忽略了裂缝的起裂状态．Shah[8]明确指出混凝土裂缝断裂过程中裂缝起裂的概念，即裂缝开始缓慢扩展的起始点．徐世烺[9]首先提出将起裂韧度作为裂缝起裂的判别准则，并将起裂韧度定义为裂缝起裂时外荷载对应于裂缝尖端的应力强度因子．因此，起裂韧度可看作材料抵抗裂缝起裂扩展的能力．

近年来，考虑起裂韧度的模型在混凝土断裂力学领域得到了一定的应用．起裂韧度可通过起裂荷载进行计算，而起裂荷载的试验确定方法可分为直接测量法和间接识别法两种．1）使用应变测试技术[10]、光弹贴片法、激光散斑法[9]等方法可直接测量起裂荷载．2）通过读取P-CMOD曲线的线性段与非线性段的拐点，来间接识别起裂荷载[11-12]．此外，徐世烺和Reinhart[13]提出将起裂韧度和失稳韧度分别作为裂缝起裂的双K判别准则，并提出了该断裂准则参数简单的解析计算方法．卿龙邦和李庆斌[14]提出了基于峰值荷载的断裂韧度理论计算方法．在模拟裂缝扩展分析方面，目前考虑起裂韧度的断裂全过程研究较少．吴智敏等[15]、董伟等[16]采用起裂韧度作为裂缝起裂扩展的判别准则，利用混凝土三点弯曲梁试件，采用有限元方法提出了混凝土裂缝的断裂过程模拟方法，并研究了断裂过程区长度及裂缝扩展阻力曲线随荷载变化的规律．李庆斌等[17]考虑起裂韧度作用，利用楔入劈拉试件分析了不同黏聚力分布对断裂全过程的影响，其研究表明黏聚力分布形式对裂缝扩展荷载下降段具有一定的影响，而对断裂峰值状态的影响较小．

鉴于混凝土非线性断裂问题的复杂性，且考虑起裂韧度的模型能较好的反映混凝土的起裂机理，因此，发展基于起裂韧度准则的简化断裂分析方法就具有较大的科研价值．

本文基于混凝土裂缝非线性断裂的黏聚力模型，采用起裂韧度扩展准则，发展了简化的混凝土裂缝断裂全过程的分析方法．结合现有的混凝土楔入劈拉断裂试验成果，对本文断裂预测方法进行了计算和验证．

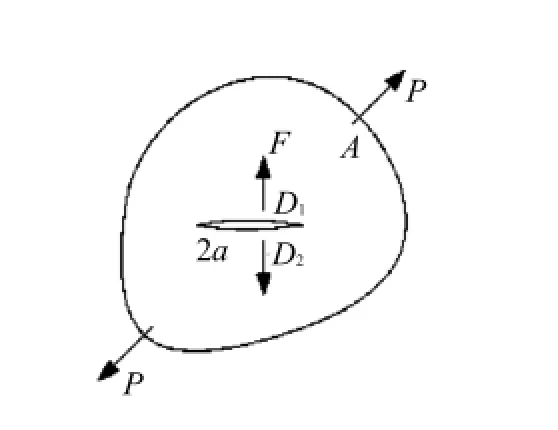
图1 虚力对和相对位移Fig.1 Virtual forceand the relative displacement

1 分析方法

1.1 裂缝张开位移表达式

如图1所示，含裂缝的单位厚度板受外力P的作用．假想沿裂缝面上D1、D2连线方向引入一对虚力F，Paris根据Castigliano法则和线弹性断裂力学原理，推得裂纹面上下两点D1、D2沿其连线方向的相对位移[18]：

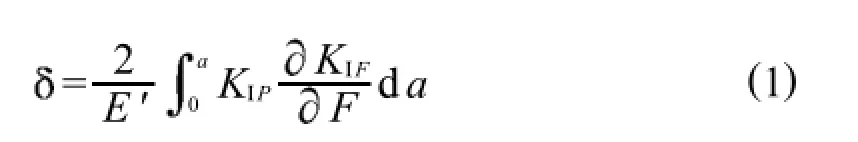
其中：对于平面应力问题，E'=E；平面应变问题，E'=E/1 v2；E为弹性模量；v为泊松比．KIP、KIF分别代表力P和力F分别提供的应力强度因子．式(1)也称为Paris位移公式．

对于如图2所示的带裂缝有限尺寸构件，在缝端坐标χ处引入一对虚力F，点对力F在有效裂缝尖端处的应力强度因子可采用断裂力学方法计算．利用权函数方法表示时，其表达式如式(2)：

根据Kumar和Barai[19]关于权函数方法的研究，将mχ,a采用四阶多项式表示

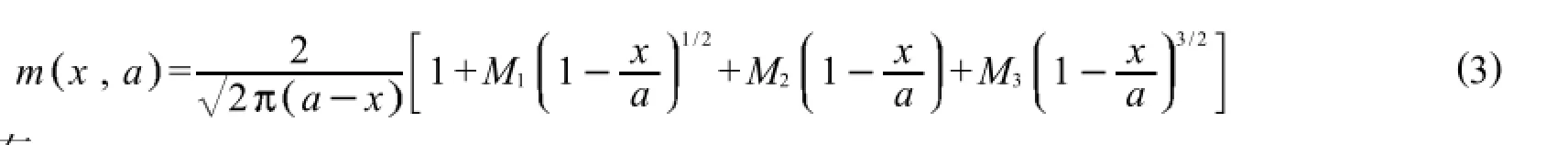
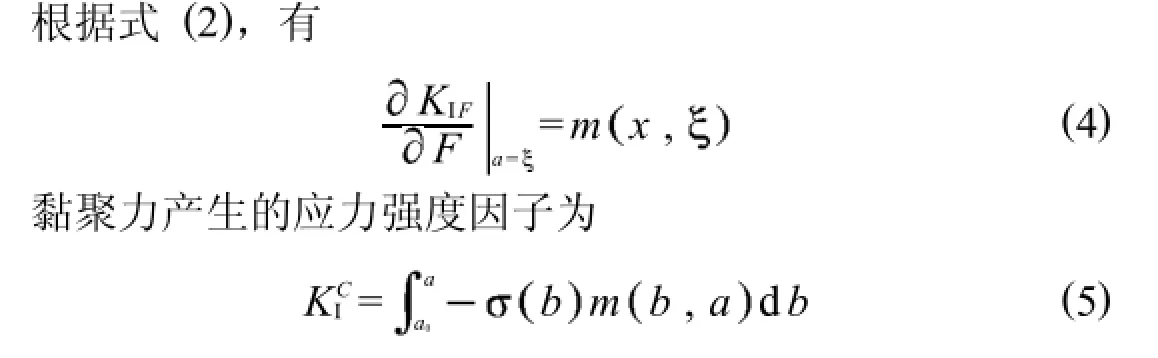
根据文献[17]，采用起裂韧度作为裂缝扩展准则时，黏聚力分布形式对峰值状态计算结果影响较小，因此，为简化计算，本文假定黏聚力采用线性分布．其中，假设初始裂缝尖端处的黏聚力与裂缝尖端张开位移满足拉伸软化曲线关系[13]．此时，可将黏聚力产生的应力强度因子表示为式(6)．

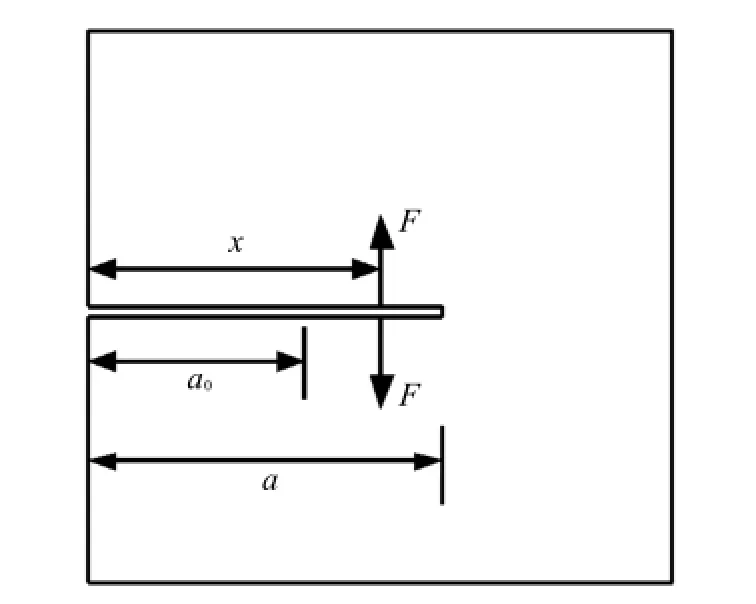
图2 点对力作用图Fig.2 A pair of force

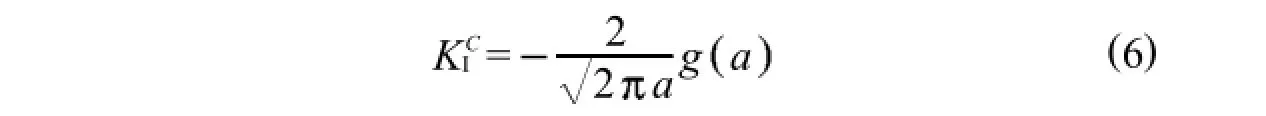
其中，c1，c2，wc为材料参数．

将式(18)代入式(17)，可得到外荷载随裂缝尖端张开位移和有效裂缝长度的表达式．

以上即为考虑起裂韧度后裂缝扩展过程中的裂缝张开位移表达式和外荷载表达式．

2 分析步骤

根据文献[17]，将断裂全过程分为起裂前、起裂后两个阶段．其中，起裂前可直接采用线弹性断裂力学公式进行计算，以起裂韧度参数作为起裂的判断标志．起裂后随着裂缝逐渐扩展，以裂缝有效长度作为加载方式，计算每一步裂缝扩展量对应的裂缝张开位移、外荷载等参数，以有效缝长即将扩展到试件的边界作为计算停止的标志．

起裂前阶段：

由于起裂前裂缝尖端张开位移和裂缝扩展长度值均为零，因此只需计算外荷载随裂缝嘴张开位移的变化曲线即可．具体步骤如下：1）将试验的起裂韧度参数代入线弹性断裂力学应力强度因子公式（式(10)），求出起裂荷载；2）将外荷载从零逐渐增大，通过式(16)计算外荷载随裂缝嘴张开位移的变化曲线；3）当外荷载增大至起裂荷载时，停止计算．

起裂后扩展：

起裂后，裂缝开始扩展．根据以上两节的推导可知，裂缝尖端张开位移表达式(15)、外荷载表达式(17)、拉伸软化曲线(18)等3式中含有外荷载、黏聚力大小、裂缝尖端张开位移、有效裂缝长度等未知数．若任意给定裂缝扩展长度值或裂缝尖端张开位移值，其它量即可通过联立该3式求解．因此，将裂缝扩展长度由零逐渐增大，即可求得CTOD-a、P-a等曲线．

按照以上的分析步骤，对于给定的黏聚力分布模型，若已知试验的起裂荷载以及拉伸软化曲线，即可唯一确定裂缝起裂前与扩展阶段的变化曲线．

由于裂缝扩展阶段采用了裂缝扩展长度加载的方式，所以对于峰值后，若仍继续增加裂缝扩展量，可通过式(15)～式(18)直接计算出峰值后裂缝扩展阶段的解答．

以上即为考虑起裂韧度及黏聚力的裂缝断裂过程分析方法．依据本文的计算思路，在实际试件的断裂分析中，只需利用起裂韧度参数判别裂缝起裂，考虑黏聚力作用，即可模拟裂缝断裂过程．

3 计算结果验证

采用文献[22]报道的混凝土断裂试验对本文计算方法进行验证．文献[22]给出了不同尺寸试件的起裂荷载、峰值荷载和临界裂缝嘴张开位移．以一级配楔入劈拉混凝土试件为例，不同尺寸的试件编号为依次为WS13～WS17，试件厚度B均为200mm．试件的有效高度D及长度H为300～1 200mm依次变化，相应的初始裂缝长度a0依次为150～600mm，具体数值如表1所示．

表1 试件尺寸与试验参数Tab.1 Specimen sizesand parameters

不同尺寸试件计算的峰值荷载状态结果见表2所示，其中，Pini为实测开裂荷载，ac为稳定裂缝扩展长度，Pmax为峰值荷载，CMODc为临界裂缝嘴张开位移．计算的荷载～裂缝嘴张开位移（P～CMOD）全曲线及荷载～裂缝尖端张开位移（P～CTOD）全曲线分别见图3、图4．

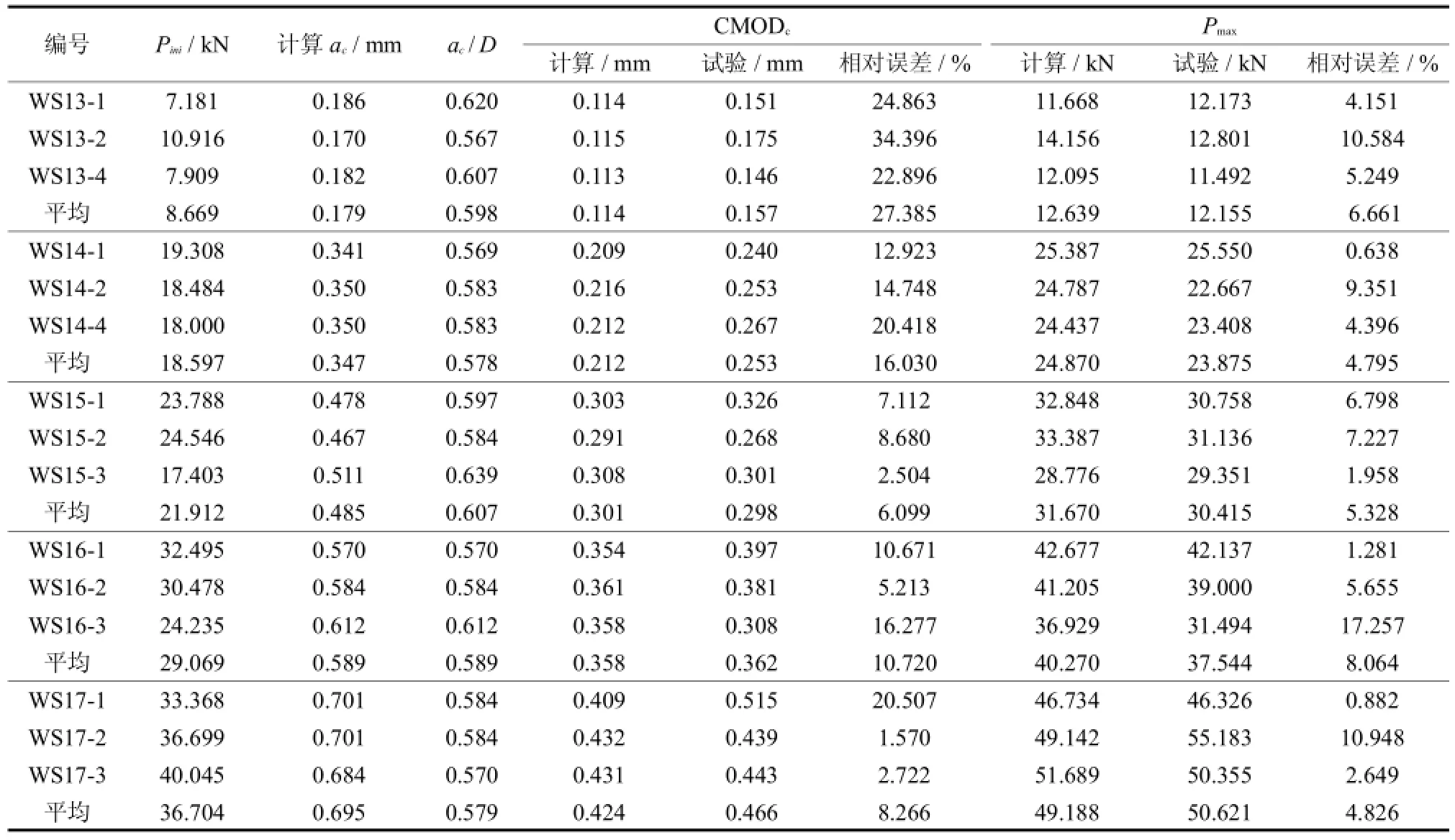
表2 计算结果与试验结果比较Tab.2 Comparison between theexperimentaldata and the calculation results

不同尺寸试件的平均峰值荷载值与试验结果比较见图5，由表2及图5可以看出，采用本文方法计算的峰值荷载与试验计算结果对比较好．不同尺寸试件计算结果的平均相对误差依次为6.661%、4.795%、5.328%、8.064%、4.826%．表明本文方法能够有效的预测构件的极限承载能力，从而验证了本文计算方法的合理性．

不同尺寸试件计算的平均CMODc相对误差依次为27.385%、16.030%、6.099%、10.720%、8.266%．当试件高度小于600mm时，计算的CMODc误差较大．其可能的原因是，为解析的表达黏聚力产生的应力强度因子，本文假定黏聚力沿黏聚裂缝面为线性分布．但当试件高度大于600mm时，采用本文方法计算结果与试验对比较好．总体来看，随着试件尺寸逐步增大，计算误差有逐渐减小的趋势．

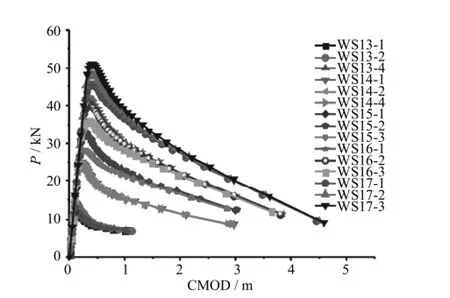
图3 P-CMOD全曲线Fig.3 Thewhole P-CMOD curves

不同尺寸试件临界相对有效缝长比（临界有效缝长与试件有效高度的比值）的平均值与文献[22]的双K方法解析结果对比见图6所示．可以看出，除WS15系列试件外，本文计算结果略小于双K方法计算的结果，其主要的原因是，双K方法采用了线性渐进叠加假定，而采用本文方法计算有效缝长时考虑了黏聚力的作用．但随着试件高度逐渐增大，其差值逐渐减小．

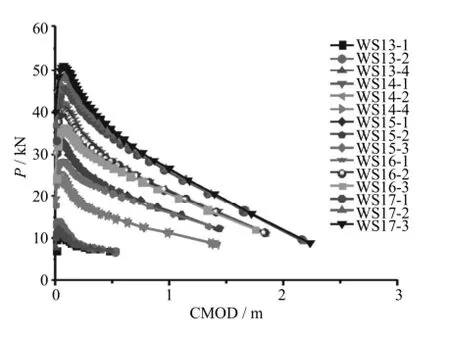
图4 P-CTOD全曲线Fig.4 Thewhole P-CTOD curves

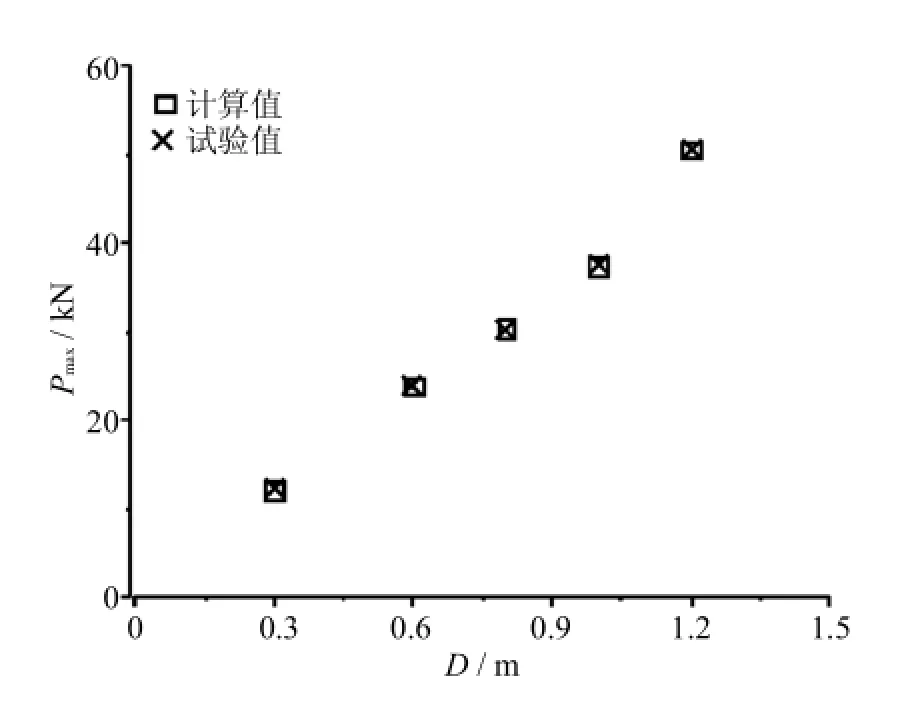
图5 不同高度试件峰值荷载的平均值Fig.5 Theaverage valuesofpeak load ofspecimens w ith differentheights

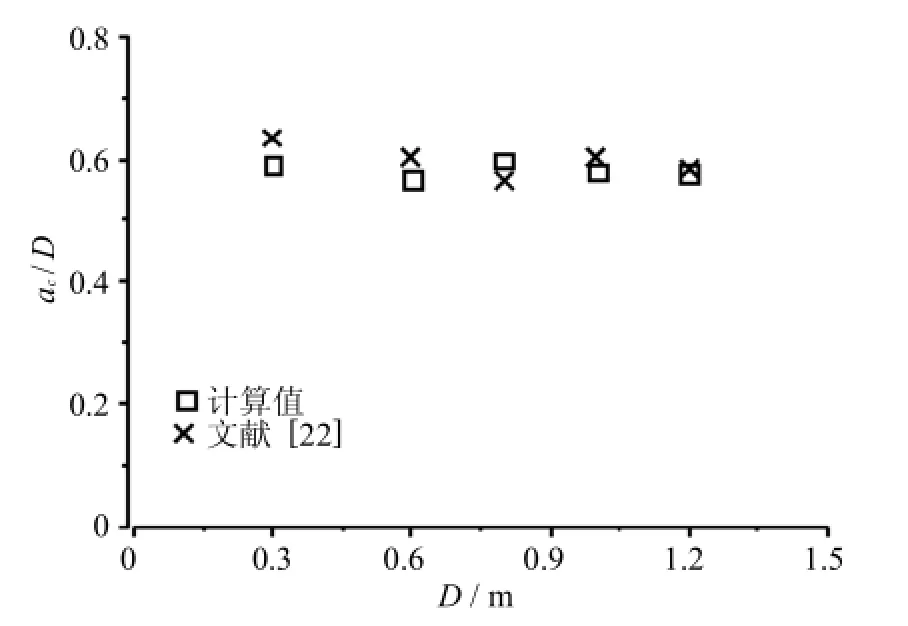
图6 不同高度试件临界相对有效缝长的平均值Fig.6 Theaverage valuesof critical relativeeffective fracture length of specimensw ith differentheights

4 结论

本文基于拉伸软化曲线推导了裂缝扩展过程中的外荷载与裂缝张开位移关系表达式，发展了混凝土裂缝断裂全过程的简化分析方法，利用楔入劈拉试件获得了裂缝扩展的全过程曲线．依据现有的混凝土断裂试验资料，采用本文提出的分析方法计算了不同尺寸试件的混凝土裂缝断裂全过程曲线，并与实测试验数据进行了比较．结论如下：

本文方法计算的峰值荷载与试验对比较好，表明本文方法能够有效的预测构件的极限承载能力，从而验证了本文方法的合理性．

采用本文方法计算的相对有效缝长结果略小于采用双K方法计算的结果，但随着试件高度逐渐增大，其差值逐渐减小．

本文方法既考虑了起裂前的计算，又能反应起裂后混凝土的软化特性，求解理论完备，可有效的预测混凝土裂缝断裂全过程．

[1]Kaplan M F．Crack propagation and the fracture of concrete[J]．ACIJournal Proceedings，1961，58（5）：591-609．

[2]Jenq Y S，Shah SP．Two Pararneter fracturemodel for concrete[J]．Journal of Engineering M echanics，1985，111（10）：1227-1241．

[3]BazantZP．Size effectin blunt fracture:concrete,rock,metal[J]．Journalof Engineering Mechanics，1984，110（4）：518-535．

[4]Karihaloo B L，NallathambiP．Effective cracksmodel for the determ ination of fracture toughnessofconerete[J]．Engeering FractureM echanics，1990（4/5）：637-645．

[5]Hillerborg A，M odeer M，Petersson P E．Analysis of crack formation crack grow th in concretebym eansof fracturemechanicsand finiteelements[J]．Cementand ConcreteResearch，1976，6（6）：773-782．

[6]李庆斌，张楚汉，王光纶．用虚拟裂缝模型研究混凝土裂缝扩展的边界单元法[J]．工程力学，1993，10（3）：9-16．

[7]BazantZP，Oh B H．Crack band theory for fracture of concrete[J]．Material and Sturcture，1983，16（93）：155-166．

[8]Shah S P，Swartz S E，Ouyang C．Fracturemechanics of concrete:applications of fracture mechanics to concrete，rock and other quasi-brittle material[M]．New York：JohnWiely Sons Inc，1995．

[9]徐世烺，赵国藩．混凝土断裂力学研究[M]．大连：大连理工大学出版社，1991．

[10]赵志方．基于裂缝黏聚力的大坝混凝土断裂特性研究[D]．北京：清华大学，2004．

[11]ReinhardtHW，Xu SL．Crack extension resistancebasedon the cohesive force in concrete[J]．Engineering FractureMechanics，1999，64：563-87．

[12]Zhang J，Leung K Y，Xu SL．Evaluation of fractureparametersof concrete from bending testusing inverse analysisapproach[J]．Materialand Sturcture，2010，43（6）：857-875．

[13]Xu SL，ReinhardtHW．Determ ination of double-K criterion for crack propagation in quasi-brittle fracture,Part IIICompact tension specimensand wedgesplitting specimens[J]．International Journalof Fracture，1999，98：179-193．

[14]Qing LB，LiQB．A theoreticalmethod fordeterrmining initiation toughnessbasedonexperimentalpeak load[J]．Engineering FractureMaterials，2013，99：295-305．

[15]吴智敏，董伟，刘康，等．混凝土I型裂缝扩展准则及裂缝扩展全过程的数值模拟[J]．水利学报，2007，38（12）：46-52．

[16]DongW，Wu ZM，Zhou X M．Calculating crack extension resistance of concrete based on a new crack propagation criterion[J]．Construction and Building Materials，2013，38：879-889．

[17]李庆斌，卿龙邦，管俊峰．混凝土裂缝断裂全过程受黏聚力分布的影响分析[J]．水利学报，2012，43（增）：38-43．

[18]Paris PC，Erdogan F．A criticalanalysisof crack propagation laws[J]．Trans Journalof Basic Engineering，1963，85：528-534．

[19]Kumar S，BaraiSV．Determ ining the double-K fracture parameters for three-pointbendingnotched concretebeamsusing weight function[J]．Fatigure&Fracture of Engineering Materials&Sturctures，2010，33：645-660．

[20]KumarS，BaraiSV．Determining double-K fractureparametersof concrete forcompacttensionand wedgesplitting testsusingweight function[J]．Engineering FractureM echanics，2009，76：935-948．

[21]ReinhardtH W，Cornelissen H A W，Hordijk D A．Tensile tests and failure analysis of concrete[J]．Journal of Structural Engineering，1986，112（11）：2462-2477．

[22]徐世烺，周厚贵，赵洪波，等．各种级配大坝混凝土双K断裂参数试验研究-兼对水工混凝土断裂试验规程制定的建议[J]．土木工程学报，2006，39（11）：50-62．

[责任编辑 杨屹]

A simplifiedmethod for predicting nonlinear fractureof concrete

QING Long-bang1，2，LIU Huan-huan1，LUO Dan-ni3，TIANWen-ling1，2

(1.Schoolof Civil Engineering,HebeiUniversity of Technology,Tianjin 300401;2.Civil Engineering Technology Research Center ofHebeiProvince,Tianjin 300401,China;3.State Key Laboratory ofHydroscienceand Engineering,Tsinghua University,Beijing 100084,China)

Cracksare thekey issue for thesafety ofconcretestructure.A sim p lifiedmethod forpredicting concrete fracture w as proposed in this paper on the basis of the initial fracture toughness criterion and the cohesive stressmodel.The expressionsof crack openingdisplacementand loadwerederivedby assum ing thedistributionof the cohesivestresses.Based on the tensilesoftening curve,thegoverningequations forconcrete fracturewereobtained,and thewhole fractureprocess curves from the crack initiation state to thepropagation statewerecalculated.In thismethod,the initial fracturetoughness criterion was adopted as crack propagation criterion,and the stress intensity factor and the crack opening displacement w ere calculated by weight function.The proposed method wasused to calculate the w hole fracture processes of wedge sp litting specimensw ith differentsizes,and the resultsw ere comparedw ith existing test results.The resultsdemonstrated that the whole process of fracture can be accurately calculated and the ultimate bearing capacity of the specimen can be predicted.The reasonability of the proposedmethod was thus verified.

concrete;crack;fracture;initial fracture toughness;cohesive stress

TV 431；TU528

A

1007-2373(2015)01-0089-07

10.14081/j.cnki.hgdxb.2015.01.017

2013-12-22

国家自然科学基金（51309073）；河北省自然科学基金（E2014202257）；高等学校博士学科点专项科研基金（20131317120012）；清华大学水沙科学与水利水电工程国家重点实验室开放基金（sklhse-2014-C-02）

卿龙邦（1982-），男（汉族），讲师，博士．