基于ANSYS的车路系统力学分析

梁晓琳，乔建刚，2

（1.河北工业大学 土木工程学院，天津 300401；2.河北省土木工程技术研究中心，天津 300401）

1945年，Burm ister D M提出了弹性层状体系理论，从而解决了层状体系在静载作用下的力学分析.但是由于车辆荷载的复杂性及繁琐的方程推导，用解析法来计算往往得不到所期望的理论解，随着计算机技术的发展，有限元软件逐步应用到道路结构的力学分析中来.同济大学苏凯等人利用有限元软件分析了行车荷载及路面结构对车辙的影响[1]；邓琼等对动载作用下半刚性路面垂直动力响应进行了有限元模拟，得到了各结构层垂直动位移和垂直动应力分布规律[2]；高建红利用有限元软件分析了轮载作用下沥青路面的弯沉分布状况，得到了弯拉应力的变化规律[3].本文以某道路改建工程为依托，借助于大型通用有限元软件 ANSYS分别对静载和动载下路面结构的力学响应进行数值求解，为道路病害的预防提供理论依据.

1 静力学分析

1.1 有限元模型的建立

选用多层路面结构，应用弹性层状体系理论进行分析，即材料具有线弹性特性.以某道路改建工程为依托，通过大量的实验确定表面层参数，其他各结构层参数由文献 [ 4]得到，如表1所示.

当汽车停驻在路面上时，其作用力为静态压力，主要是由轮胎传给路面的垂直压力，按照我国现行路面设计规范中规定的标准轴载BZZ-100的轮载，进行分析[5].采用大型通用有限元分析软件ANSYS建模，单元采用三维六面体8节点等参元，路面模型的尺寸为3m×3m×3.67 m.通过参考文献，分析时取均布矩形荷载，作用面积为233.0 mm×173.04 mm[6].边界条件假设为：底面上 =0；左右两侧 =0；前后两侧 =0，层间接触情况为完全连续.有限元计算模型如图1所示.

表1 路面结构各层材料参数Tab.1 Materialparametersof the pavementstructure

图1 静力学路面结构有限元模型Fig.1 The finiteelementmodelof the pavement structureunder static action

1.2 静力学响应分析

路表弯沉表征路面结构在设计标准轴载作用下，垂直方向的位移.由图2、图3可知，车辆荷载作用下路表沉降最大值发生在轮胎与路面接触面的中心，为0.339mm，方向沿 轴负方向.轮隙弯沉并非是路表弯沉的最大值，但可以作为弯沉分布的一个特征点.由图4可见，应力随距轮隙中心竖向距离的变化而变化. 方向应力先增大后减小最后趋于平缓，最大值出现在深度122 mm处，始终表现为压应力； 方向应力先由拉应力变为压应力再变为拉应力，最大压应力值也出现在深度122mm处，变化趋势类似于 方向应力； 方向应力由压应力变为拉应力，变化趋势是先减小后增大再减小.

图2 路表弯沉曲线Fig.2 Deflection curveof road surface

图3 路面结构各层位移云图Fig.3 Displacementcontoursof pavementstructure

2 动力学分析

2.1 建立有限元模型

车辆对路面作用的实质是轮胎对路面的碰撞激励[7-8].路面结构层参数依然采用表1数据，路面模型的尺寸及边界条件假设同静力学模型.轮胎模型的胎体是由实体橡胶材料构成，轮辋选用半刚性材料，用质量单元表示车身质量，用弹簧单元表示车辆减震系统，其尺寸和具体参数根据相关文献选取[9-10].采用ANSYS瞬态分析模拟轮胎与路面的碰撞过程.其有限元模型如图5所示.

2.2 动力学响应分析

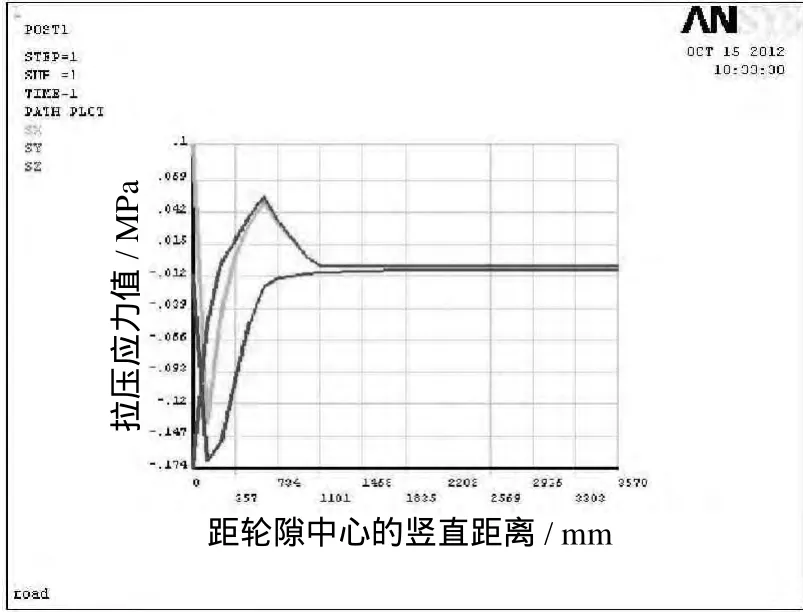
图4 竖向应力曲线Fig.4 Verticalstress curve

图5 动力学轮胎/路面结构有限元模型Fig.5 The tire/pavement finiteelementmodel under dynam ic action

从图6中可以看出，碰撞中心点的位移是随着时间呈现出先增大后减小的规律.0～0.01 s是碰撞刚接触过程，有一个瞬间小的位移变化量，方向为 轴负方向；0.01～0.107 s是完整的碰撞接触过程，位移随着接触时间的增加而增大，其中，在0.01～0.06 s时间段内，由于碰撞的冲量作用，使得位移变化速率大，0.06 s以后位移缓慢增加，0.107 s达到位移最大值0.209 167mm（方向为 轴负方向）；0.107～1 s为路面回弹过程，回弹方向为 轴正方向，其中0.107～0.15 s，位移-时间曲线斜率最大，为瞬间回弹过程，分析其原因为荷载瞬间抽离，部分被压缩能量瞬间释放，0.15 s后被压缩位移缓慢回弹，由于计算时间长，回弹时间限制为1 s，位移最终回弹到0.022 mm，但从图上可以看出，曲线仍有回弹趋势，这与实际情况是相符合的.图7是碰撞中心点 方向应力随时间的变化规律，可以看到在碰撞刚接触的时候，由于冲击力的作用压应力值最大，随着时间慢慢减小趋于零.

图7 时间- 方向应力曲线Fig.7 Time-stress in Z direction curve

3 轮隙弯沉值的对比分析

表1中路面结构组合的轮隙弯沉值如表2所示.其中解析解由设计弯沉值计算公式得到，DRFP程序解由文献 [3]得到，数值解由ANSYS软件计算得到.

表2 轮隙弯沉值Tab.2 Tiregap deflection

由表2可知，轮隙弯沉值的大小顺序为：解析解→DRFP程序解→ANSYS静力学计算值→ANSYS动力学计算值→实测值.解析解和DRFP程序解很接近，这是由于两者所用的理论体系和基本假定几乎完全相同，但由于其中的一些基本假设、边界条件、接触条件等不完全符合路面结构的实际情况，所以结果和实测值相差较大.静力学分析结果，轮隙弯沉值为0.339mm，与实测值相差0.134mm，相对误差值为65.37%；动力学分析结果，轮隙弯沉值为0.209mm，与实测值相差0.004mm，相对误差值为1.95%.十分接近实测值.一定程度上也说明了所建道路三维有限元模型在约束、施加荷载、不同材料层之间的处理、单元选择等方面都是合理的.如图8所示，通过对比动力学计算值与静力学计算值与实测值的相对误差，可知 ANSYS软件动力学分析模拟车路系统的结构力学响应更为有效.

4 结语

通过以上的分析，分别得到了动、静荷载下位移最大值及应力随时间、深度的变化规律，为道路病害的预防提供了理论依据；轮隙弯沉值的对比分析结果表明了用静力学分析路面结构的力学响应误差较大，这是因为静力学分析忽略了路面的阻尼，这与实际道路材料存在偏差；用动载代替静载进行车路系统的动力学分析，考虑了路面阻尼的影响，所得结果十分接近实测值；使用动力学分析路面的结构力学响应还存在一些问题：如分析中采用的是固定位置的动荷载，既考虑大小的随机性又考虑荷载沿空间位置变化的理论研究还未取得实质性进展，希望在接下来的研究中能突破此技术难关.

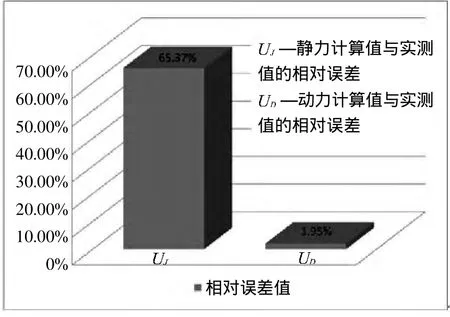
图8 静力、动力学轮隙弯沉值与实测值的相对误差Fig.8 Relativeerrorbetween measured values andwheel gap deflection analog valuesunder static,dynam ic action

[1]苏凯，孙立军.行车荷载及路面结构对车辙影响的有限元分析[J].同济大学学报：自然科学版，2007，35（2）：187-192.

[2]邓琼，张淳.动载作用下半刚性路面垂直动力响应三维有限元模拟[J].公路工程，2008，33（3）：68-71.

[3]高建红.沥青路面弹性层状体系的三维有限元仿真分析 [J].交通科技，2006（1）：28-30.

[4]高明星，徐海林.橡胶颗粒沥青路面/轮胎噪声的有限元分析 [J]内蒙古农业大学学报，2010，31（3）：188-192.

[5]郭红兵，王宁，吕光印.轮胎-沥青路面接触效应数值分析 [J].郑州大学学报：工学版，2011，32（1）：34-37.

[6]胡小弟.轻型货车轮胎接地压力分布实测 [J].公路交通科技，2005，22（8）：1-7.

[7]李韶华.重型汽车与路面耦合作用研究 [J].振动与冲击，2009，28（6）：155-158.

[8]杨建荣，李建中，范立础.基于ANSYS的车桥耦合振动分析 [J].计算机辅助工程，2007，16（4）：23-26.

[9]陈栋华，靳晓雄.轮胎刚度和阻尼非线性模型的解析研究 [J].中国工程机械学报，2004，2（4）：408-412.

[10]任旭春，张光华，洪宗跃，等.有限元在载重子午线轮胎弹性模量优选中的应用 [J].橡胶工业，2004，51（8）：464-466.