考虑扭转和畸变效应的薄壁箱梁超收敛单元研究
2015-07-18陈建芳谢雯馨罗振先
陈建芳,李 伟,谢雯馨,罗振先
(1.广西大学土木建筑工程学院工程防灾与结构安全教育部重点实验室,广西 南宁 530004;2.郑州市市政工程勘测设计研究院广州分院,广东 广州 510640)
考虑扭转和畸变效应的薄壁箱梁超收敛单元研究
陈建芳1,李 伟2,谢雯馨1,罗振先1
(1.广西大学土木建筑工程学院工程防灾与结构安全教育部重点实验室,广西 南宁 530004;2.郑州市市政工程勘测设计研究院广州分院,广东 广州 510640)
文章基于Benscoter梁理论和箱梁畸变理论,建立了一个关于薄壁箱梁约束扭转问题的2节点8自由度的超收敛单元,该单元可以精确考虑薄壁箱梁的扭转和畸变效应,只需一个单元就可得到精确解。通过与Vlasov的广义坐标法进行算例比较,证明该单元有较高的精度。
薄壁箱梁;约束扭转;畸变;单元
0 引言
薄壁梁由于其强度高、重量轻和材料利用率高的特点,被广泛用于许多工程应用中。特别是具有封闭横截面的薄壁梁,具有较高的抗扭和抗弯性能。由于闭口薄壁截面变形的复杂性,在桥梁结构和一些重要结构的设计中,扭转和畸变效应是非常重要的考虑因素。
有许多良好的有限梁单元都是基于Timoshenko梁理论,但是这些梁单元不能较为全面地考虑闭口薄壁梁[1],传统的梁单元通常具有六个自由度,三个平动位移和三个转角位移,而忽略了横截面的变形,导致高估了梁的刚度。Vlasov提出了一套较为全面的关于矩形薄壁箱梁的翘曲和畸变研究理论,在此基础上,对于薄壁梁的翘曲和畸变效应已经进行了大量研究,Vlasov提出了关于闭口薄壁梁计算的广义坐标法,该方法放弃了开口薄壁梁理论中的“刚周边”和“中面无剪应变”两个假定,利用变量分离法将二维问题转化成一维问题[2],该理论计算精度高,但计算费时[3]。Kim[1]基于广义坐标法利用拉格朗日插值推导出的单元刚度矩阵方便了计算,但仍需划分较多单元才能得到收敛解。韦芳芳[4]在广义坐标法初参数方程的基础上,通过矩阵子块转换的方式推导出在均布扭矩作用下薄壁箱梁翘曲分析的单元刚度矩阵。对于闭口薄壁箱梁的畸变效应,文献[5]介绍的传统的箱梁畸变微分方程已广泛用于箱梁的畸变分析。本文基于Benscoer梁理论和传统的箱梁畸变计算理论,采用非多项式插值,建立了一个2节点8自由度的约束扭转梁单元。
1 基于广义坐标法的单元刚度矩阵
Vlasov提出的广义坐标法适用于由平板围成的闭口截面梁考虑截面变形的约束扭转分析,该理论推导的箱梁约束扭转微分方程如下[6]:
f(6)-2r2f(4)+s4f(2)=0
(1)
式(1)可通过初参数法求的解析解,但对于一些复杂结构,很多时候求解是较为困难的,因此,常需用数值方法来计算,文献[1]采用拉格朗日插值推导出薄壁箱梁约束扭转下的单元刚度矩阵:
(2)
该单元刚度矩阵可以同时考虑扭转和畸变效应,以及两者之间的耦合作用,但需要划分较多单元时才能得到收敛解。
2 基于Benscoter梁理论的扭转单元刚度矩阵
传统的Vlasov开口薄壁梁理论考虑了约束扭转引起的翘曲位移,但忽略了截面在厚度方向的横向剪应变,对于开口薄壁截面影响较小,但对于闭口薄壁截面将产生较大的误差。
Vlasov给出的开口薄壁杆件的翘曲位移:
ux=ω(y,z)θ′(x)
(3)
Benscoter采取一个翘曲函数Ψ替换扭率θ′,纵向的翘曲位移则为[7]:
u=ω(s,ζ)Ψ(x)
(4)
其中ω仍为Vlasov理论中假设的广义扇形坐标,但考虑了厚度方向的横向剪切变形。

图1 薄壁梁截面曲线坐标图
薄壁梁截面的曲线坐标如图1所示,假设薄壁梁截面上任意一点p的位移为:
u(x,s,ζ)=ω(s,ζ)Ψ(x)
vqt(x,s,ζ)=-(rn(s))+ζ)θx(x)
(5)
vqn(x,s,ζ)=rt(s)θx(x)
式(5)中u为纵向翘曲位移,vqt为s方向的切向位移,vqn为法向位移。
由位移函数根据几何方程和物理方程得到应变和应力,再应用虚功原理得到微分方程:
Ψ=θ′+αθ‴
θ″″-γ2θ″=0,
(6)



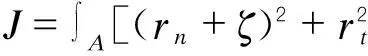
采用式(4)的齐次解作为插值函数,再由内外虚功相等得到控制方程:
[kθ]{uθ}={fθ}
(7)
其中

(8)
{uθ}=[θx1Ψ1θx2Ψ2]T;
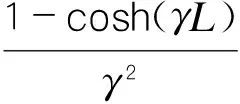
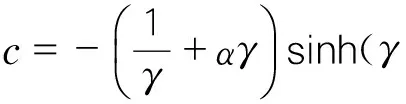
当单元上作用均布扭矩mx时,等效节点荷载:
[fθ]=[Mθ1Bθ1Mθ2Bθ2]T
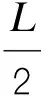
3 畸变荷载下的畸变计算理论


(9)
采用齐次解作为插值函数,得到单元刚度矩阵方程:
[kχ]{uχ}={fχ}
(10)



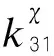
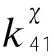
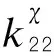

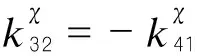
(11)

4 建立同时考虑扭转和畸变效应的闭口薄壁梁单元刚度矩阵
Vlasov的广义坐标法已成为闭口薄壁梁的扭转和畸变效应研究的基础,并且计算精度高,但计算费时,尽管在广义坐标法的基础上推导出的有限元格式方便了计算,但对单元划分数要求较高,本文结合前面推导的扭转单元刚度矩阵和畸变理论下的单元刚度矩阵,建立了一个2节点8自由度的闭口薄壁梁单元。
在此不考虑扭转与畸变之间的耦合作用,采用直接刚度法,形成单元刚度矩阵:
(12)
节点位移列阵和均布扭矩下等效节点荷载列阵分别为:
{u}=[θx1Ψ1χ1χ′1θx2Ψ2χ2x′2]T;
{f}=[Mθ1Bθ1Mχ1Bχ1Mθ2Bθ2Mχ2Bχ2]T。
5 算例分析
为了验证本文推导出的单元刚度矩阵的正确性,采用文献[3]的算例与广义坐标法的解析解进行比较,矩形闭口薄壁梁一端固定,一端自由,尺寸如图2所示,自由端受一集中扭矩Mx=1 000N·cm,其中弹性模量E=2.1×107N/cm2,泊松比μ=0.25,均匀等壁厚t=1cm。

图2 悬臂梁所受荷载和尺寸图
采用文献[6]的单元刚度矩阵计算结果如表1(表中只列出自由端的扭转角和畸变角)所示:

表1 文献[6]方法计算结果分析比较表
从表1中的计算结果可以看出,按文献[6]方法计算,当划分到20个单元时畸变角的计算结果才收敛,即逼近广义坐标法的解析解2.628×10-5rad。

表2 本文方法与广义坐标法解析解的比较表
从表2中的计算结果可以看出,采用本文单元计算时,只划分了一个单元就可以得到自由端的收敛解,与广义坐标法解析解的计算结果相当吻合。当划分10个单元时,本文方法与广义坐标法解析解的比较如图3所示,显然,在梁的各个横截面上,用本文方法计算得到的扭转角与畸变角的值与广义坐标法解析解的计算结果几乎完全吻合。


图3 悬臂梁扭转角和畸变角比较示意图
再看一个源自文献[6]的算例,两端固支受均布扭矩mx=1 000 N·cm/cm,如图4所示,比较梁各横截面上的扭转角和畸变角。

图4 两端固支梁受均布扭矩图
本文方法划分10个单元时,与广义坐标法的解析解比较扭转角和畸变角的计算结果,如图5所示。
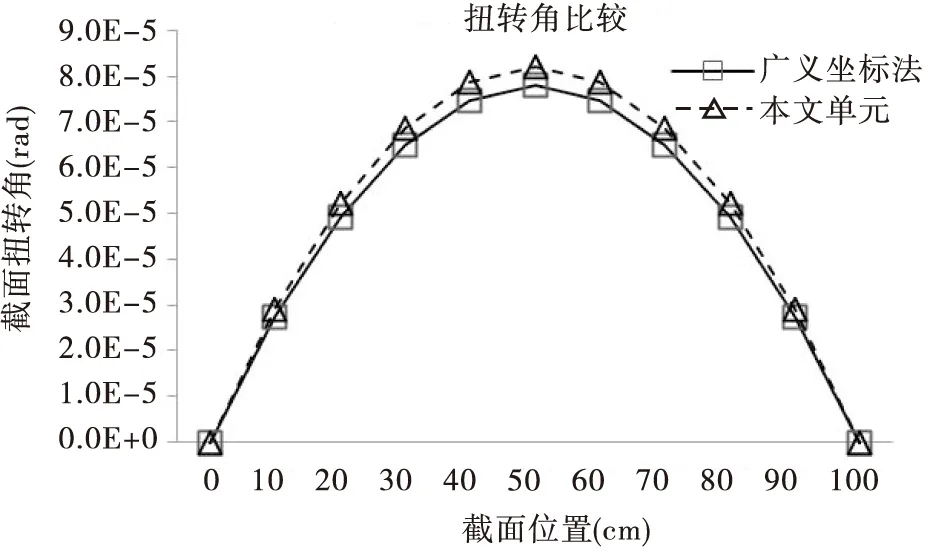

图5 两端固支梁受均布扭矩计算结果对比图
从图5的计算结果可以看出,在均布扭矩作用下,本文方法的计算结果与广义坐标法的解析解非常吻合,具有较高的计算精度和效率。
6 结语
从算例分析结果可以看出,本文推导的2节点8自由度的闭口薄壁扭转梁单元计算的结果与Vlasov的广义坐标法计算结果相当吻合,可以同时考虑扭转和畸变效应,是一个超收敛单元,对于工程应用具有较高的实用价值,计算效率高,并且有较高的计算精度。
[1]Kim Y Y,Kim J H.Thin-walled Closed Box Beam Element for Static and Dynamics Analysis[J].International Journal for Numerical Methods in Engineering,1999,45(4):473-490.
[2]杨绿峰,赵艳林,李桂青.闭口薄壁杆件约束扭转计算的样条里兹法[J].工程力学,1999,1(1):181-187.
[3]鲍永方,黄文彬.矩形箱梁约束扭转理论的分析与比较[J].工程力学,1997,14(3):132-137.
[4]韦芳芳,吴 京,冯 健,等.薄壁箱梁广义坐标法刚度矩阵的推导及应用[J].计算力学学报,2007,24(5):693-697.
[5]周 履.单室矩形箱梁畸变计算[J].桥梁建设,1980(4):1-45.
[6]包世华,周 坚.薄壁杆件结构力学[M].北京:中国建筑工业出版社,2006.
[7]Shakourzadeh H,Guo Y Q,Batoz J L.A Torsion Bending Element for Thin-walled Beams with Open and Closed Cross Sections[J].Computers & Structures,1995,55(6):1045-1054.
[8]谢 旭,黄剑源.薄壁箱形梁桥约束扭转下翘曲、畸变和剪滞效应的空间分析[J].土木工程学报,1995,28(4):3-14.
Research on Super-convergent Element of Thin-walled Box Girder Considering the Torsion and Distortion Effects
CHEN Jian-fang1,LI Wei2,XIE Wen-xin1,LUO Zhen-xian1
(1.Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education,College of Civil Engineering and Architecture,Guangxi University,Nanning 530004,China)
2.Guangzhou Branch of Zhengzhou City Municipal Engineering Design & Research Institute,Guangzhou 510640,China)
This article,based on Benscoter beam theory and box girder distortion theory,established a 2-node super-convergent element with 8 degrees of freedom about restrained torsion problem of thin-walled box girder,this element can accurately consider the torsion and distortion effect of thin-walled box girders,only one element is needed to get the exact solution.Through calculation comparison with Vlasov’s generalized coordinate method,it proved that this element has a higher accuracy.
Thin-walled box girder;Restraint torsion;Distortion;Element
陈建芳(1962—),副教授,硕士生导师,主要从事计算结构力学及其工程应用方面的研究工作。
广西理工科学实验中心重点项目(LGZX20 1101);广西自然科学基金项目(2013GXNSF BA019237)
U448.21+3
A
10.13282/j.cnki.wccst.2015.07.008
1673-4874(2015)07-0029-05
2015-06-08
