基于动网格与UDF技术的内杆做行星运动的环空中流场数值模拟
2015-07-18庞博学杨树人刘丽丽马立辉
庞博学,杨树人,刘丽丽,刘 超,张 莹,马立辉
(东北石油大学,黑龙江 大庆 163000)
基于动网格与UDF技术的内杆做行星运动的环空中流场数值模拟
庞博学,杨树人,刘丽丽,刘 超,张 莹,马立辉
(东北石油大学,黑龙江 大庆 163000)
应用动网格技术以及UDF程序成功实现了内杆在油井偏心环空中自转同时公转的行星运动状态。完成了内杆在井筒偏心环空中不同偏心率位置转动的情况下,流体在井筒环空中流动的数值模拟。计算结果表明,内杆偏心率增加,流体周向运动增强,湍流高黏度区域扩大,层流区域相应增加。存在一临界偏心率εr,在其两侧,流体作用力分别将内杆离心外推和向心内拉。且内杆偏心率越大,流体内推力就越大,流体对内杆公转运动方向上的阻力也越大。
动网格;UDF;行星运动;Fluent;偏心率
对于内杆静止的偏心环空中的流动,前人做了大量的研究工作。与内杆静止的偏心环空流动相比较,当内杆自转与公转同时进行时,流体在此种环空中的流动要更加复杂,人们对这种流动的研究少之又少[1]。在石油钻井工程中,尤其是对于水平井和定向井,钻杆因受自身重力的影响,在井筒中是弯曲的,再加上电动机驱动钻杆的自转,在井筒与钻杆所形成的偏心环空中的钻井液的流动就属于内杆做行星运动的环空中的流动问题[2]。与此相似,在采油工程尤其是螺杆泵采油中,由于内杆偏心,抽油杆在自转的同时还沿外管轴线公转,在该环空中采出液的流动也属于内杆做行星运动的环空中的流动问题[3]。由此可见,此种流动在工程实际中常常遇到。
本文旨在应用计算流体动力学的方法,通过编译UDF程序实现内管行星运动状态,应用Fluent动网格技术对内杆行星运动的环空中的流动问题进行数值求解。此举可以为定向井和水平井等工况钻井液的水力参数设计,以及螺杆泵采油生产工况的优化提供理论指导方向,具有学术价值和工程实践意义[4]。
1 动网格技术在内杆行星运动中的应用
1.1 模型简化
内杆行星运动环空流场简化模型如图1所示。将石油工程实际中所描述的问题做如下简化:流体处于内、外2个偏心的圆管构成的环空中,外圆管静止,内圆管以恒定的角速度ω自转,又以恒定的角速度Ω沿外圆管轴线公转,并有沿外圆管轴线方向的压力P作用在流体上。

图1 内杆行星运动环空流场简化模型
1.2 动网格方法
为实现环空中内杆的行星运动,数值模拟应用动网格技术,如图2所示。内杆运动使得流体几何区域变化剧烈,动网格更新方法采用局部网格重构模型(remeshing),动区域选择指定刚体运动(rigid body)。模拟计算过程中,因动边界导致局部网格超过定义的最大尺寸时网格一分为二,局部网格受挤压紧缩低于定义的最小尺寸时合二为一,当网格扭曲程度超过定义的倾斜度时亦重新划分,以适应运动区域的形态变化。被重新划分的网格单元紧邻动网格节点,运动边界附近网格得到及时更新[5]。

图2 内杆自转及内杆自转且公转动网格瞬态图
动网格任意控制体V,通用标量Φ的积分守恒方程为:
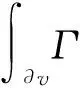
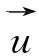
时间导数项可由一阶向后差分项用如下公式表示:
式中,n和n+1是当前时间及下一层时间。
第n+1时间层上的体积Vn+1为:
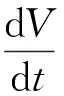
式中,dV/dt是控制体的时间导数。
为满足网格守恒律,控制体的体积时间导数为:

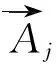
每个控制容积面上的点积为:
式中,δVj是整个时间步Δt上控制容积面j膨胀引起的体积改变。
2 UDF的编译及求解模型的选择
2.1 内杆行星运动的用户自定义函数(UDF)的编译
UDF是为满足计算个性化需求,可以动态地连接到Fluent求解器上的用户自编的程序。通过UDF调用动网格宏(DEFINE_CG_MOTION)可实现刚体运动边界的控制。内杆运动UDF编译的主体思想如模型简化图。自转通过DEFINE_CG_MOTION宏中的omega[z]实现,公转通过控制内杆旋转速度矢量vel[x]、vel[y]以及动网格矢径完成。
2.2 数值求解条件及模型选择
定义流体密度ρ为0.8×103g/m3,流变指数n为0.6,外管内径R为40 mm,内杆外径r为20 mm,内杆自转速度ω为30 rad/s,公转速度Ω与ω相同,为30 rad/s,环空流体轴向压力梯度为300 Pa/m。
此次内杆行星运动的环空流场数值计算对控制方程的离散应用有限体积法,采用分离式求解器求解。选择k-epsilion 湍流模型,并开启能量方程,用中心差分格式离散扩散项,选择PRESTO!格式对压力项离散,其余用一阶迎风离散,压力速度耦合方程采用PISO算法,使用编译型UDF文件定义刚体速度,动网格采用局部网格重构方法,对内杆行星运动的环空流场进行非定常求解[6]。
3 偏心环空螺旋流与内杆行星运动的环空中的流动
偏心环空螺旋流是仅有内杆自转的环空中的流动,而内杆行星运动的环空中的流动则是在偏心环空螺旋流的基础上,增加内杆以角速度Ω绕外管轴线公转的情况。分别模拟计算偏心环空螺旋流与内杆行星运动的环空中的流动有助于分析内杆公转对流场的影响。
3.1 偏心环空螺旋流与内杆行星运动环空中流体的速度场计算
通过流场周向速度分布图(见图3)可以得出结论:在仅有内杆自转的偏心环空螺旋流中,由于黏性力的作用,内杆的自转促使其壁面附近区域流体产生周向速度,速度标量值以内杆轴线为圆心呈环形区域分布,且由内杆壁面沿径向逐渐减小。而在内杆行星运动的环空中,由于内杆在环空中的偏心公转,被转动波及的流体区域更大,流体周向速度最大值保持在靠近内管壁环空窄间距侧。
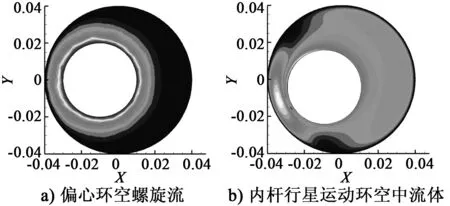
图3 流场周向速度分布图
3.2 偏心环空螺旋流与内杆行星运动环空中流体的压力场计算
通过流体动态压力分布图(见图4)可以得出结论:在偏心环空螺旋流中,流体作用力峰值出现在内杆壁表面,且内杆周向受力基本均匀;而在内杆行星运动的环空中,流体作用力峰值保持在内杆公转迎流面窄间距处,即流体有阻止内杆公转并将内杆向环空内侧推回的趋势。

图4 流体动态压力分布图
4 内杆偏心程度对流场的影响
在内杆自转且公转的环空流动中,流体与内杆存在相互作用力,内杆在流体中转动的同时伴有横向扰动, 这种扰动使得内杆公转半径即相对于外管的偏心距在时刻变化,流体对内杆的径向作用力与内杆偏心程度相互作用。由于内杆偏磨、失稳等情况与偏心率密切相关,因此有必要针对不同偏心率对内杆行星运动流场的影响计算分析。
定义内杆偏心率ε=e/emax,其中e是内杆相对于外管轴线的偏心距,emax是最大偏心距(即内杆外壁接触外管内壁的完全偏心),此模型中,emax=20 mm。分别模拟计算内杆偏心率ε=0.25、ε=0.5以及ε=0.75时内杆行星运动的环空流体场。
4.1 不同偏心率环空流体周向速度场分布
通过不同偏心率环空流场周向速度分布图(见图5)可以得出结论:由于内杆在环空中的偏心公转,随着偏心距的增加,被转动波及的流体区域扩大,流体周向运动增强,速度标量值增大。
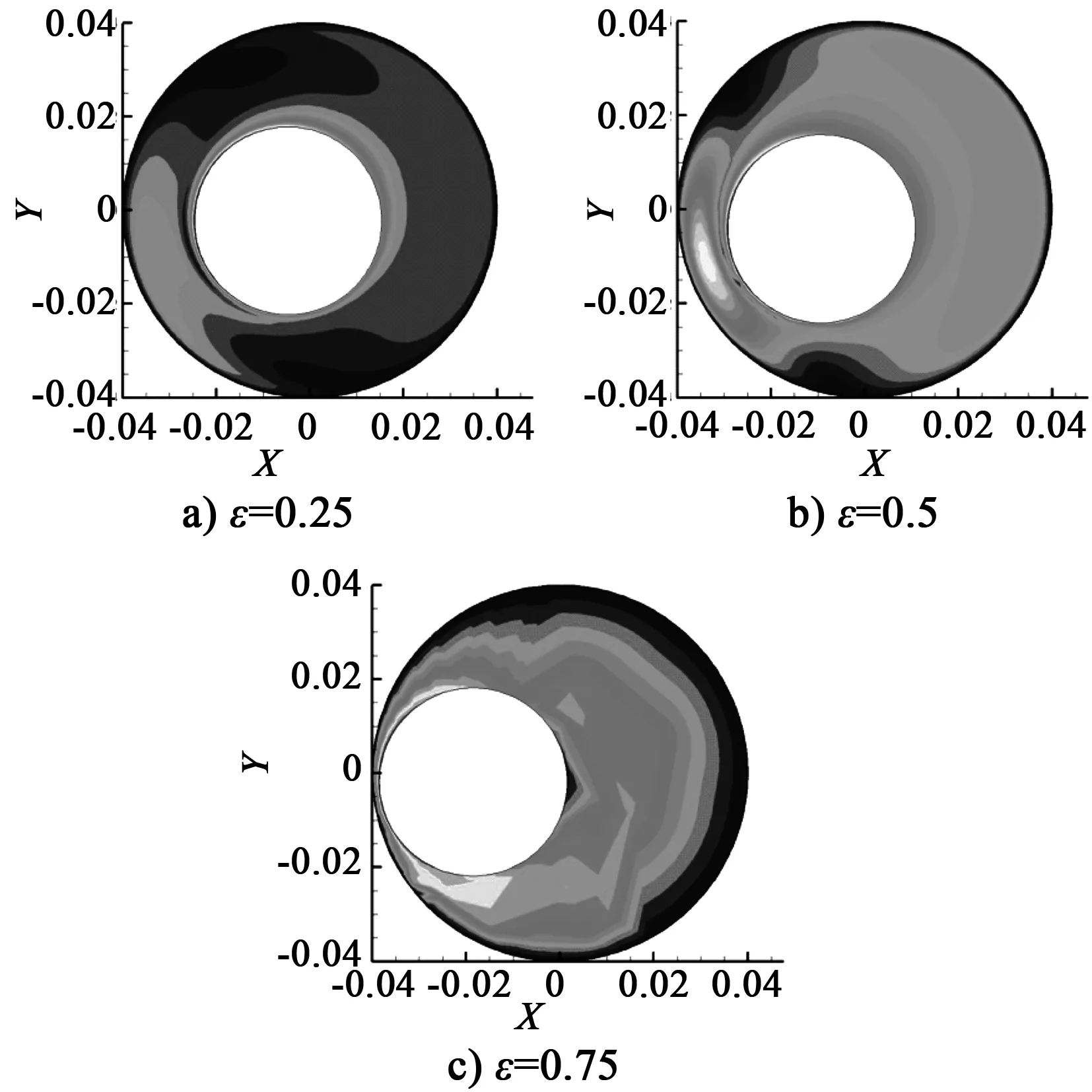
图5 流场周向速度分布图
4.2 不同偏心率环空流体湍流强度分布
通过不同偏心率环空流场湍流强度分布图(见图6)可以得出结论:内杆偏心距对流场湍流强度影响明显,湍流强度峰值集中出现在环空宽间距侧,且随着偏心距的增加,湍流强度减弱,层流区域增加。
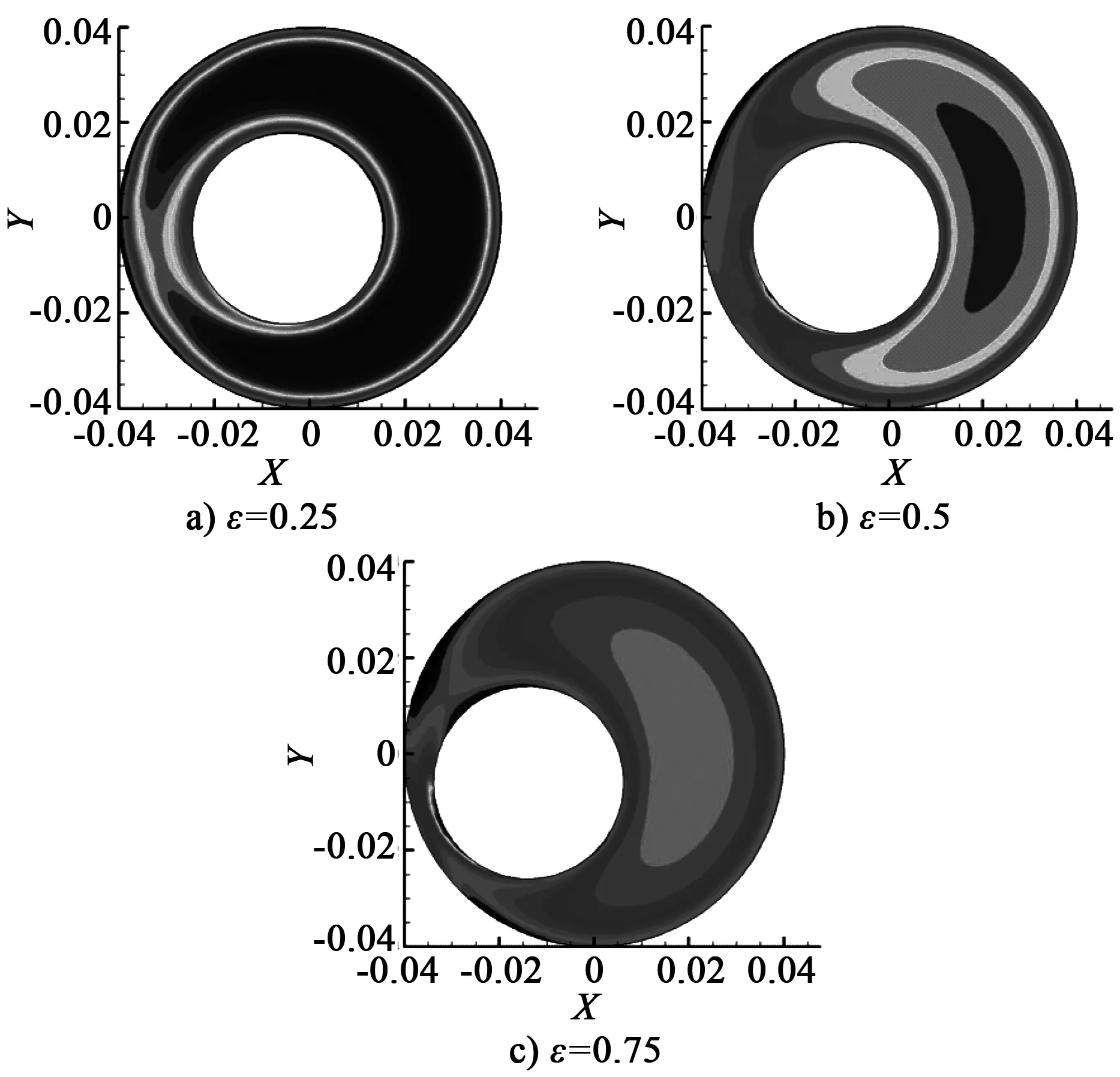
图6 流场湍流强度分布图
4.3 不同偏心率环空流体高黏度区域分布
通过不同偏心率环空流场湍流黏度分布图(见图7)可以得出结论:由于内杆在环空中旋转导致漩涡,涡流扩散使得流体产生远大于分子水平的表观黏度,即湍流黏度,使组分黏度增加,湍流黏度峰值区域集中出现在宽间距侧,但绕内杆转动方向出现旋转偏移。且偏心距越大,湍流高黏度区域越大。
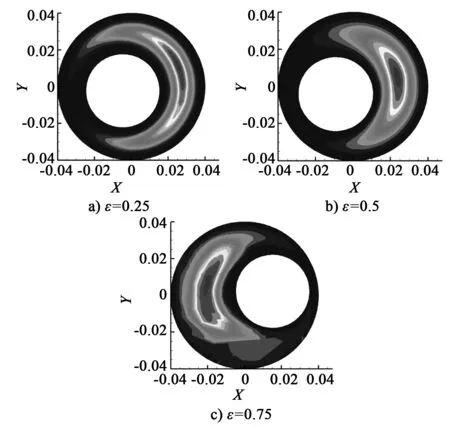
图7 流场湍流黏度区域分布图
4.4 偏心率对内杆在环空中所受流体力的影响
内管在环空流体中转动的过程中,流体作用力将影响内管受力平衡,此作用力由流体压强和周向剪应力综合作用产生[7]。将流体作用力F分解为沿公转路线径向上的流体力Fj和沿公转路线切向上的流体力Fq。定义Fj正方向指向公转轨道轴心,Fq正方向与内杆公转运动速度矢量方向一致。分别模拟内杆偏心率ε为0.05、0.20、0.35、0.50、0.65、0.80及0.95情况下行星运动时的流体场,计算得出内管所受流体沿公转路线径向的作用力Fj和沿公转路线切向的作用力Fq,绘制如图8所示曲线。
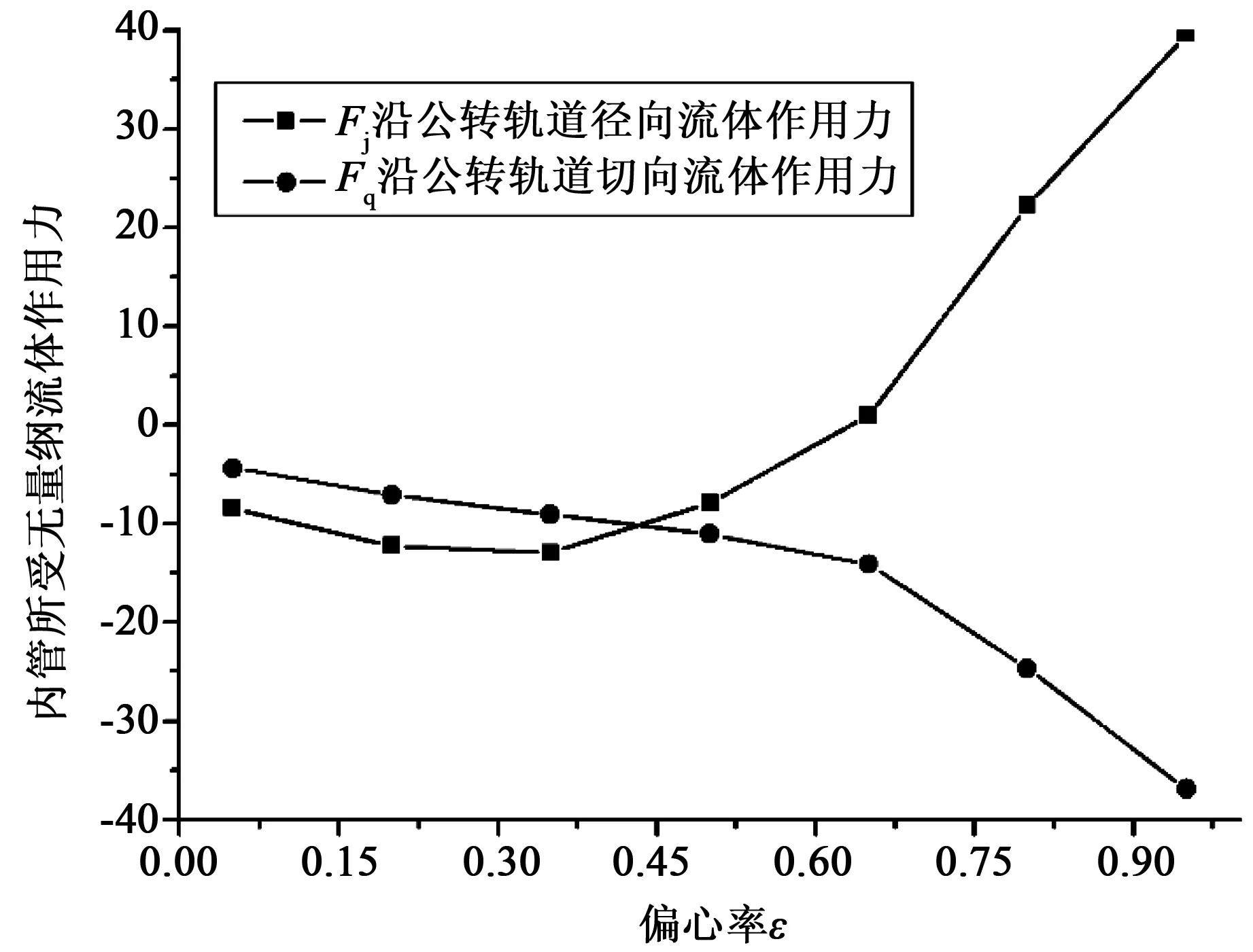
图8 内杆在不同偏心率ε下所受流体作用力曲线
通过不同偏心率环空流场内杆所受流体作用力曲线可以得出结论:内杆在公转轨道径向上(Fj方向)所受流体作用力一般情况下不平衡。存在临界偏心率εr(约为0.65),使得当ε<εr时,Fj始终小于零,流体作用力有将内杆向离心方向外推的趋势;ε>εr时,Fj始终大于零,流体作用力有将内杆向公转轨道轴心方向内推的趋势,且偏心率ε越大,内推作用力越大。而在公转轨道切向上(Fq方向),内杆所受到的流体作用力始终小于零,说明流体力一直在阻止内杆沿公转轨道的运动,内杆偏心率越大,流体阻力越大。
5 结语
应用Fluent动网格技术和UDF可以成功实现偏心环空中内杆的行星运动。对内杆在不同偏心率下行星运动的环空中的流动研究得出如下结论。
1)随着内杆偏心率ε的增加,被转动波及的流体区域扩大,流体周向运动增强。
2)内杆旋转导致涡流扩散使得流体产生远大于分子水平的湍流黏度,其峰值区域在环空宽间距侧,但绕内杆转动方向出现旋转偏移。随着偏心距的增加,湍流高黏度区域扩大,湍流强度减弱,层流区域增加。
3)存在临界偏心率εr:当ε<εr时,流体作用力将内杆向离心方向外推;当ε>εr时,流体作用力将内杆向轴心内推,偏心率越大,内推作用力越大,流体对内杆公转运动方向上的阻力越大。
[1] 崔海清,张淑云,修德艳,等. 流体在内管做行星运动的环空中流动的压力梯度[J]. 中国石油大学学报:自然科学版,2008(6):76-78,87.
[2] 裴晓含. 幂律流体在内管做行星运动的环空中流动时内管壁的受力分析[D].大庆:大庆石油学院,2007.
[3] 季海军. 幂律流体在内管做行星运动的环空中的流动[D].大庆:大庆石油学院,2005.
[4] 杨树人. 粘弹性流体偏心环空非定常流的数值计算[D].大庆:大庆石油大学,2006.
[5] 张来平,邓小刚,张涵信. 动网格生成技术及非定常计算方法进展综述[J]. 力学进展,2010(4):424-447.
[6] 杨树人,庞博学,刘丽丽. 天然气井应用涡流工具排水采气的流场分析[J]. 石油矿场机械,2014(10):13-16.
[7] 冯顺新,李启兵,符松. 内管自转且公转时环管幂律流的受力分析[J]. 计算力学学报,2008(2):212-217.
责任编辑彭光宇
NumericalSimulationofFlowFieldinEccentricAnnulusWhoseInnerTubehasPlanetaryMotionbasedonDynamicMeshandUDF
PANG Boxue,YANG Shuren,LIU Lili,LIU Chao,ZHANG Ying,MA Lihui
(Northeast Petroleum University, Daqing 163000,China)
Movement of the inner tube rotation and revolution in eccentric annulus was achieved successfully by means of dynamic mesh and UDF. The flow in the annulus whose inner tube at different eccentricity rotates and revolves simultaneously was simulated. The results showed that: with the eccentricity increase, circumferential movement of fluid enhance, aera of high turbulent viscosity and laminar region expanded. There was a critical eccentricity on each side of which fluid force pushed inner tube outward and pulled it inward. The larger the eccentricity was, the greater fluid force that pulled inner tube inward was. Furthermore, resistance to the motion of the inner tube in the direction of revolution by fluid becomed larger.
dynamic mesh, UDF, planetary motion, Fluent; eccentricity

TH 311
:A
庞博学(1991-),男,硕士研究生,主要从事复杂流体流动与数值模拟等方面的研究。
2014-12-28
