基于MATLAB的给定连杆预定位置的四杆机构设计
2015-07-18韩二豹
韩二豹
(陕西工业职业技术学院,陕西 咸阳 712000)
基于MATLAB的给定连杆预定位置的四杆机构设计
韩二豹
(陕西工业职业技术学院,陕西 咸阳 712000)
连杆机构是一种典型的机械机构,其运动设计是一个比较复杂和困难的问题。对于给定连杆预定位置的四杆机构的设计,常用的设计方法为解析法。以MATLAB语言为基础,利用计算机对给定连杆预定位置的四杆机构进行设计。结果表明,该方法设计过程简洁,结果合理、准确,效率高。
四杆机构;MATLAB;预定位置
MATLAB是一种高级技术语言和开发环境[1],它提供了一个人机交互的系统环境,并以矩阵作为基础的数据结构,节省编程时间,语法简单,容易掌握,调试方便,可以设置调试断点、快速查找程序错误等。MATLAB将使用者从繁重、重复的计算中解脱出来,已经被大家认可和广泛使用,充分展现了高效、直观和简单的特点。MATLAB是用于分析数据、开发算法和应用面向函数的语言,可以方便地进行工程数值分析、优化分析、数据处理和自动控制,也可以实现计算可视化、图形绘制图像处理和仿真等功能,在工业和研究领域具有极大的使用价值,逐渐成为优化领域的主要工具之一。MATLAB可以快速解决传统办法很难解决的问题,在实际应用中具有很大的优势。
1 设计步骤[2-3]
1)建立可靠的优化设计的数学模型及约束条件。
2)根据参数的数学模型运用MATLAB进行编程[4],确立主程序和子函数并进行调试和求解运算。
3)给定参数,估算初始值,利用函数求解,得到结果。
4)结果分析。
2 可靠性数学模型的建立
四杆机构如图1所示,设计该机构的核心是求活动铰链中心B和C。在机架建立固定坐标系oxy,以M为原点,在连杆上建立动坐标系Mx'y',M→N为x'轴的正向。点B、C在动坐标系的坐标为(xB',yB')、 (xC',yC'),在固定坐标系的坐标为(xB,yB), (xC,yC),可以得到:
(1)
(2)
式中,φi为x轴正向至x'轴正向沿逆时针方向的夹角。

(3)
固定铰链中心A、D在固定坐标系中的位置坐标为 (xA,yA)、(xD,yD),可以得到:
(xBi-xA)2+(yBi-yA)2=(xB-xA)2+(yB-yA)2(i=1,2,3,…,n)
(4)
(xCi-xD)2+(yCi-yD)2=(xC-xD)2+(yC-yD)2(i=1,2,3,…,n)
(5)
如果事先给定A、D的位置,利用上述公式,可以精确实现连杆3个预定位置的计算,式4和式5还可以划归为线性方程求解[5]。
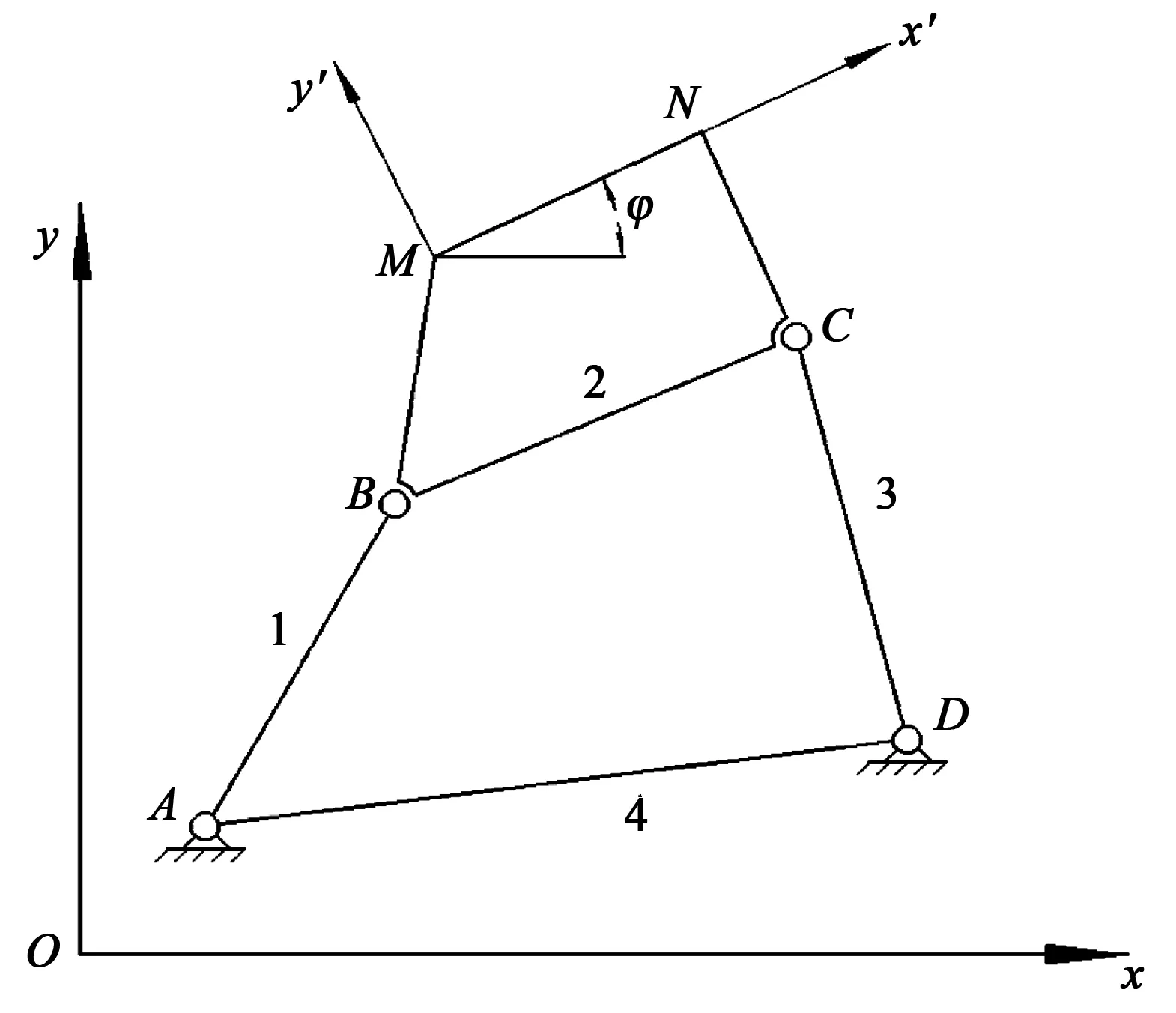
图1 四杆机构
3 优化设计实例
已知连杆2的3个位置:xp1=10 mm,yp1=35 mm,φ1=53°;xp2=34 mm,yp2=40 mm,φ2=30°;xp3=40 mm,yp3=27 mm,φ3=0°。选定机架上2个固定铰链坐标为A(0,0)、D(60,0),设计以该刚性构件为连杆的铰链四杆机构。编写的MATAB 程序由link_fun_Main、link_fun_B和 link_fun _C等3部分组成。
link_fun_Main
clear; xp1=10; yp1=35; phi1=53*pi/180; xa=0,ya=0;xd=60;yd=0;
% AB 长度的计算
x=[0;0]; x=fslove(@link_fun_B,x);
xb1=xm1+x(1)*cos(phi1)- x(2)*sin(phi1);
yb1=ym1+x(1)*sin(phi1)+x(2)*cos(phi1);xb=xb1;yb=yb1;
% CD 长度的计算
X=[35;46];x=fslove(@link_fun_c,x);
xc1=xm1+x(1)*cos(phi1)- x(2)*sin(phi1);
yc1=ym1+x(1)*sin(phi1)+x(2)*cos(phi1);xc=xc1;yc=yc1;
% BC长度的计算
lbc=sqrt((xc1-xb1) ^2+(yc1-yb1) ^2)
lad=sqrt((xa-xd) ^2+(ya-yd) ^2)
% 输出
disp(' 结果1:BC 坐标(单位 mm)')
disp(' x y ')
fprintf('B %3.2 f ',xb,yb);
fprintf('C %3.2 f ',xc,yc);
disp(' 结果2:各杆长度(单位 mm)')
fprintf('曲柄长度 %3.2 f ',lab);
fprintf('连杆长度 %3.2 f ',lbc);
fprintf('摇杆长度 %3.2 f ',lcd);
fprintf('机架长度 %3.2 f ',lad);
%子函数link_fun_B
Function F =link_fun_B(X)
xm=[10;34;40];ym= [35;40;27]; phi=[53;30;0]*pi/180;
xa=0;ya=0;
%求B在固定坐标系的坐标
For i=1:3
xb(i)=xm(i)+x(1)*cos(phi(i))- x(2)*sin(phi(i));
yb(i)=ym(i)+x(1)*sin(phi(i))+x(2)*cos(phi(i));
end;
%求B在固定坐标系的方程
F=[(xb(2)-xa)^2+(yb(2)-ya)^2-(xb(1)-xa) ^2-(yb(1)-ya) ^2; (xb(3)-xa)^2+(yb(3)-ya)^2-(xb(1)-xa) ^2-(yb(1)-ya) ^2];
%子函数link_fun_C
Function F =link_fun_C(x)
xm=[10;34;40];ym= [35;40;27]; phi=[53;30;0]*pi/180;
xd=63;ya=0;
%求C在固定坐标系的坐标
For i=1:3
xc(i)=xm(i)+x(1)*cos(phi(i))- x(2)*sin(phi(i));
yc(i)=ym(i)+x(1)*sin(phi(i))+x(2)*cos(phi(i));
end;
%求C在固定坐标系的方程
F=[(xc(2)-xd)^2+(yc(2)-yd)^2-(xc(1)-xd) ^2-(yc(1)-yd) ^2; (xc(3)-xd)^2+(yc(3)-yd)^2-(xc(1)-xd) ^2-(yc(1)-yd) ^2];
该程序运行显示结果如下:
结果1:B C 坐标(单位 mm)
x y
B -3.26 -10.20
C 66.26 31.25
结果2:各杆长度(单位 mm)
曲柄长度 l1=10.72
连杆长度 l2=80.94
摇杆长度 l3=64.08
机架长度 l4=60.00
结果符合四杆机构和曲柄存在条件。
4 结语
针对连杆机构的运动设计解析法和综合法的复杂性和困难性,根据机构运动几何关系,在建立数学模型的基础上,运用MATLAB软件中的求解非线性方程、线性方程组和优化计算功能, 可以方便、快捷、准确地得到计算结果。
[1] 葛超,王蕾,曹秀爽.MATLAB技术大全[M].北京:人民邮电出版社,2014.
[2] 陈立德.机械设计基础[M]. 2版.北京:高等教育出版社,2004.
[3] 李滨城,徐超.机械原理MATLAB 辅助分析[M].北京:化学工业出版社,2011.
[4] 李元科.工程最优化设计[M].北京:清华大学出版社,2006.
[5] 周继瑶.现代机械中的机构优化设计[J].企业科技与发展,2013(9):19-20.
责任编辑彭光宇
BasedontheGivenMATLABReservePositionDesignofFour-barLinkageConnectingRod
HAN Erbao
(Shanxi Polytechnic Intitute,Xianyang 712000,China)
The connecting rod mechanism is a kind of typical mechanical mechanism, its motion design is a complex and difficult problem, and the design method of common four bar mechanism given link predetermined location as the main analytical method. This paper is based on the MATLAB language, the design of four bar mechanism is linked to the predetermined position given by computer. The results show that this method is simple, and the result is reasonable, accurate, and high efficiency.
four bar mechanism,MATLAB,the predetermined position
TB 121
:A
韩二豹(1978-),男,讲师,工程硕士,主要从事机械制造及自动化等方面的研究。
2015-01-29
