局域体缺陷对石墨烯纳米带电子输运性质的影响

刘玉良 张小伟 徐光亮

(西南科技大学四川省非金属复合与功能材料重点实验室－省部共建国家重点实验室培育基地 四川绵阳 621010)

自从石墨烯单层在2004年用机械剥离法被成功分离出来以后［1］，这种材料就因其独特的物理性能在过去的十几年中得到广泛而深入的研究［2－6］。而在实际应用方面，石墨烯纳米带(graphene nanoribbons，GNRs)更具研究价值。通常完美的GNRs存在两种边界:之字型边界(zigzag GNRs，ZGNRs)和扶手椅型边界(armchair GNRs，AGNRs)。许多研究表明，所有的ZGNRs和三分之一的AGNRs是金属性的，因为它们的带隙为零 。另外，AGNRs带结构随着纳米带宽度的变化呈现周期性重复［9－10］。

但是，实验上很难制备出完美的石墨烯纳米带。现在许多研究小组把他们的研究重点集中于存在缺陷或褶皱的纳米带［11－17］。研究表明，当存在缺陷时，纳米带的电子结构会被完全改变，从而电子输运性质亦被改变。Evaldsson 和 Han 等人［15，18］指出，若GNRs存在一定浓度的边界空位，那么金属型的GNRs将转变为半导体型的，同时还指出，当GNRs的宽度达到十几纳米以后，ZGNRs和AGNRs之间的差别就可以忽略，它们具有相似的输运性质。Zhang等研究表明［19］，当GNRs内部存在缺陷时，在缺陷周围会形成局域环形电流，从而形成微磁矩，此时GNRs对外表现出一定的磁性。发生以上这些现象的根本原因在于GNRs的电子结构由于缺陷的存在被极大地改变了。

本文基于紧束缚框架，采用递归格林函数方法研究存在体空位时ZGNRs的电子输运性质。集中对存在单原子体空位、双原子体空位和两个单原子体空位的体系进行系统的研究，并通过分析电子态的局域性来理解其物理机制。

1 模型与方法

本文采用的模型如图1(a)所示，它分为3个区域:左导线、中心样品区和右导线。为了避免界面散射和计算的方便，我们认为左右导线具有和样品一样的结构和边界形状。图1(a)中的蓝色矩形方框代表无缺陷时的一个超原胞。GNRs的电子结构可以由很多方法来计算，这里采用单－π轨道最近邻紧束缚近似框架。相应的单粒子哈密顿量表示为:

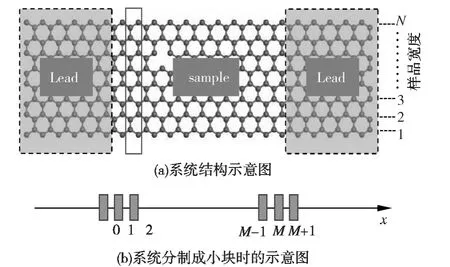
图1 系统模型Fig.1 Model of System

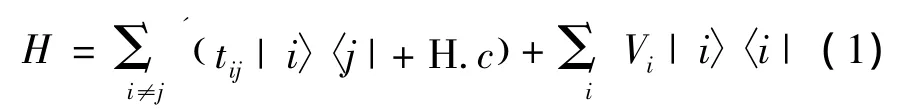
这里的Vi为第i个碳原子的格点能，求和∑遍及所有的格点。tij为最近邻的相互作用，这里取 tij=－2.7 eV，∑＇只对最近邻进行求和。

对于电导的计算，我们采用递归格林函数方法。它是一种强大而可靠的计算方法，已被广泛应用于各个领域［16，20］。这里不对递归格林函数方法作详细介绍，只简单说明几个相关的公式，我们将在本文的计算中应用这些公式。通过中心样品区的电导可以用格林函数写为［21］:

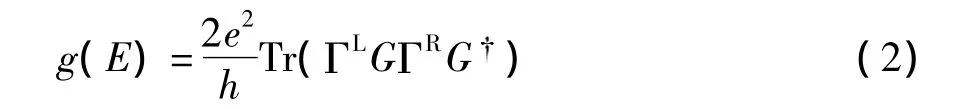
这里的G与G 分别表示整个系统(包含导线)的格林函数及其厄米共轭。ΓL，R=，其中自能函数ΣL，R包含了左右导线的影响。注意，格林函数是系统哈密顿量的倒数形式，因此在紧束缚近似下，它是一个矩阵，而‘Tr’表示求矩阵的迹。当样品包含的格点数很大时，电导的计算会占用大量的计算机资源，即使在计算机运算速度大幅提升的今天，仍然是一个巨大的挑战。因此，在本文中，我们采用递归方法来求解系统的格林函数。它的核心思想是把体系分割为许多小块，这些小块可以是等价的，也可以是不等价的，然后分别求出每个独立小块的格林函数，最后利用Dyson方程将这些小块联系起来构成整个系统的格林函数。如图1(b)所示，为了表述方便，我们用灰色小方块代表一个分割小块，这里就是图1(a)中的蓝色矩形。很清楚，标号为1－M的小灰色方块代表样品，标号小于1大于M的灰色小块代表导线。使用Dyson方程，很容易得到下面的递推公式:

这两个公式分别从左右导线出发，将样品区域的小块一个一个地连接到左右导线。最后利用公式

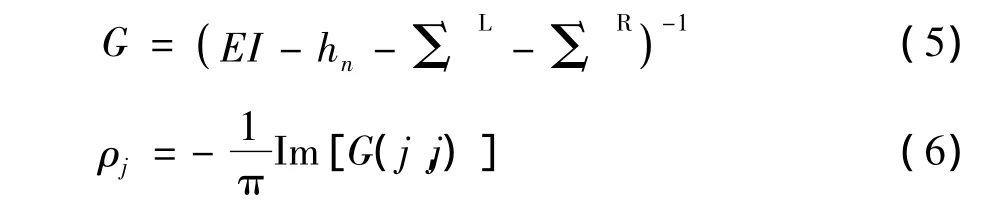
计算整个系统的格林函数和局域态密度。其中式(5)中 的 ΣL=，ΣR=，式(6)中的 G(j，j)是整体格林函数的第j个对角元，‘Im’代表虚部。这些公式不仅对本文的体系适用，对其它体系也适用。在实际的计算中，图1(b)中的灰色小块可以代表一维体系的点、二维体系的线、三维体系的面。

2 结果与讨论

在本节中，我们利用上面介绍的递归格林函数方法研究存在体缺陷时ZGNRs的电子输运性质。首先，我们研究最简单的单原子空位、双原子空位对电子输运性质的影响，这种缺陷在实验中也是最容易发生的情况之一。注意，本论文中ZGNRs的宽度N=8，长度M=100，图2是计算结果。为了方便对比，在图中我们也列出了完美ZGNR的输运曲线。很明显，它有完美的量子化台阶，和以前的研究结果一致。当ZGNR存在一个单原子体空位时(结构示意图在图2(b)的内插图中)，体系的电导受到明显的压制，但仍表现出逐步台阶化上升的趋势。值得注意的是，在费米能E=0 eV处，存在一个电导沟。换句话说，在费米能处，电导迅速下降，这和无缺陷的情况完全不同。为了分析这种现象背后的物理机制，我们计算了体空位旁边格点的局域态密度，如图2(b)所示，其中的内插图指明了相关格点的具体位置。在费米能处，局域态密度曲线和完美纳米带的情况完全不同，它有一个尖锐的锋值，这表明在体空位处存在准局域态。具体地说，当E=0 eV时，电子态局域在体空位的周围，它不能开辟一个电子通道，因此对电导没有贡献。通常电子态的局域性越好，该电子态对导电性的贡献就越小。

图2 体系的电导曲线和局域态密度Fig.2 Conductance curve of the system and local density

当系统存在一个双原子空位时，电导压制更加明显，如图2(a)红色电导曲线所示。和单原子缺陷不同，电导沟出现在完美石墨烯纳米带的第一条能带带边处，这可通过对比图2(a)中的蓝色和红色的电导曲线得出。和上面讨论类似，在这两点处将会出现准局域态，从而阻碍电导通道的形成。局域态密度的计算也表明，确实在第一条能带带边处出现峰值，如图2(c)所示，计算的格点位置在内插图指明。

综上所述，石墨烯纳米带的电导对系统的缺陷很敏感。当系统存在一个单原子或双原子体空位时，系统的电导压制已经很明显，且在能量较低时出现电导沟。可以预见，体系存在更多的空位时，电导将会受到更大的压制，要在实验上观测到完美的量子化电导台阶就更加困难。计算结果还表明，体空位在输运方向(x方向)的位置对电导曲线没有影响。也就是说，我们对电导的模拟计算是稳定的。

接下来研究体系存在两个单原子体空位时的输运性质。图3的内插图是我们研究体系的结构示意图。两个体空位之间的距离L用超原胞的个数表示，例如，内插图中两个空位之间的距离L=5。同样地，设定体系的宽度N=8，长度M=100。首先我们让两个单原子体空位在输运方向上随机地分布，并对电导进行了两次计算，如图3所示。很明显，电导仍然受到很大的压制，但两次计算的结果有明显的差异，这是因为两个体空位在两次计算中的距离不一样。同时，我们还可以从图3中清楚地看到，对电导的两次计算结果均存在共振透射峰，并且当两个体空位之间的距离增大时，电导曲线的共振透射峰数目也随之增加。以第一条能带带边为界，红色电导曲线出现了11个共振峰，它对应的L=34，而绿色电导曲线出现了4个共振峰，它对应的L=11。因此，我们猜想，两个体空位间的距离每增加3个超原胞，即L的值每增加3，电导曲线的共振峰增加一个。为了印证这个猜想，我们计算了1≤L≤11时所有电导曲线。为了对比的方便，所有曲线都放在图4中，电导的刻度并未显示，其中蓝色曲线为没有空位时的电导。同时，每条电导曲线的共振峰数目也在图中注明。可以看出，虽然存在一些差异，但L值和共振峰数目的关系基本符合我们的猜想，而且，共振峰的位置也各不相同。这些结果意味着，我们可以通过调控体空位间距来调整共振峰的数目及位置，只允许和共振峰能量相同的电子通过，从而达到滤波的目的，这在相关实验上具有一定的指导意义。

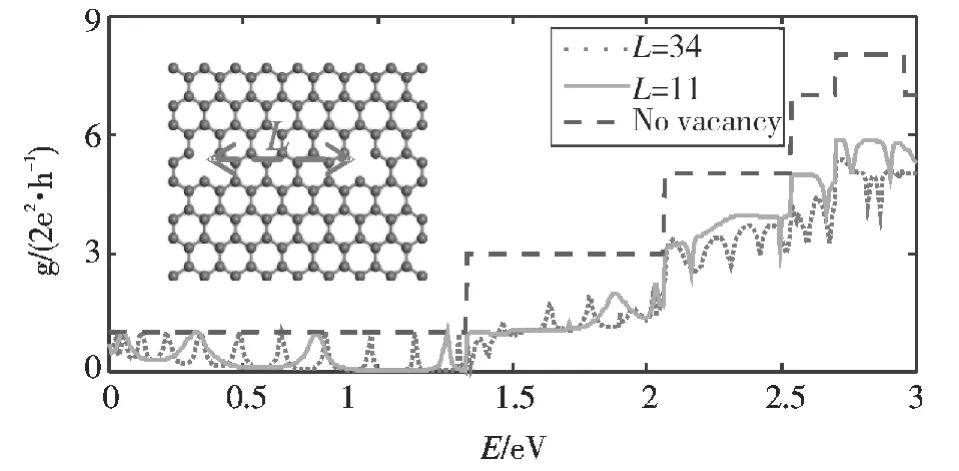
图3 体系存在两个单原子空位时的电导曲线Fig.3 Conductance curve when there exits two one－atom vacancies in the system

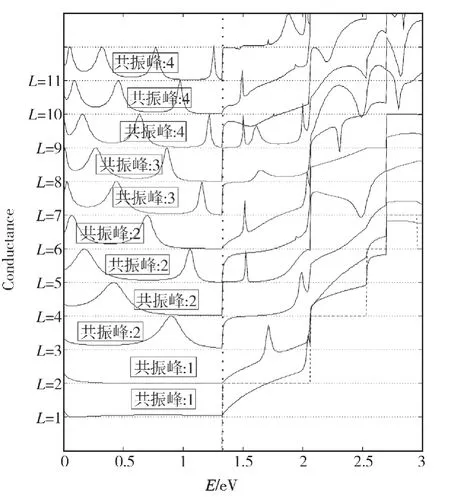
图4 存在两个单原子空位时的电导曲线(L=1～11)Fig.4 Conductance curve when there exits two－atom vacancies(L=1～11)

对于这种奇特输运现象，可以作如下定性理解。两个体空位相当于两个散射势垒。当一列入射波从左导线入射，将会受到两个势垒的散射作用，入射波的一部分被反射，另一部分被透射。一般地，散射势垒越多，透射概率越小。但是，当入射波的波长和散射势垒间的距离存在某种匹配关系时，这列波将发生共振透射。这种匹配关系和体系的晶格结构有关，而入射波的波长则直接和入射能量相关。因此，在我们研究的体系中，当电子能量和两个势垒间的距离存在这种匹配关系时，共振透射就发生了。势垒间距越大，就会有更多的入射能量满足这种匹配关系，因此，共振透射峰就越多。在我们研究的体系中，两个体空位的间距每增加3个超原胞，满足这种匹配关系的能量值就多一个，即，共振透射峰就多一个。

3 结论

本文简单介绍了递归格林函数方法，并用这种方法研究了存在体空位时ZGNRs的电子输运性质。结果表明，若ZGNRs存在体空位时，电导压制非常明显，即使这种体空位的数目很少。这就表明ZGNRs的输运性质敏感地依赖于其自身的缺陷，这对实验上观测量子化电导台阶提出了巨大的挑战。我们的计算结果还显示，当系统有一个单原子空位时，在费米能处有一个电导沟存在，而当系统有一个双原子空位时，则电导沟存在于第一能带带边处。对体空位附近的格点进行了局域态密度分析，结果表明，电导沟的存在是由于电子态局域在空位附近，不能形成有效的电子通道。对于存在两个随机分布的单原子空位时ZGNRs的电导，我们发现在低能范围内存在共振透射峰，且透射峰的数目和两个空位间的距离密切相关，当距离每增加3个超原胞时，透射峰就会增加一个，这种奇特的物理性质对相关实验具有指导意义。

［1］NOVOSELOV K S，GEIM A K，et al，Electric field effect in atomically thin carbon films［J］.Science，2004，(306):666.

［2］JIANG C，WANG X F，ZHAI M X.Spin negative differential resistance in edge doped zigzag graphene nanoribbons［J］.Carbon，2014，(68):406.

［3］JUNG J，MACDONALD A H.Accurate tight－binding models for the π bands of bilayer graphene［J］.Phys.Rev.B 2014，(89):035405.

［4］COSTA A L M T，MEUNIER V，GIRAO E C.Electronic transport in three－terminal triangular carbon nanopatches［J］.Nanotech.2014，(25):045706.

［5］YAN W，HE W Y，et al.Strain and curvature induced evolution of electronic band structures in twisted graphene bilayer［J］.Nat.Commun.2013，(4):1.

［6］ROSALES L，PACHECO M，et al.Transport properties of graphene nanoribbons with side－attached organic molecules［J］.Nanotech.2008，(19):065402.

［7］WAKABSYASHI K，FUJITA M，et al.Electronic and properties of nanographite ribbons［J］. 1999，(59):8271.

［8］PISANI L，CHAN J A，MONTANARI B，et al.Electronic structure and magnetic properties of graphitic ribbons［J］.2007，(75):064418.

［9］ZHANG X W，YANG G W.Novel band structures and transport properties form graphene nanoribbons with armchairedges ［J］. J. Phys. Chem. C， 2009，(113):4662.

［10］SON Y W，COHEN M L，LOUIE S G.Energy gaps in graphene nanoribbons［J］.Phys.ReV.Lett.2006，(97):216803.

［11］PEREIRA V M，CASTRO N A H，et al.Geometry，mechanics，and electronics of singular structures and wrinkles in graphene ［J］. Phys. Rev. Lett. 2010，(105):156603.

［12］CASTRO N A H，GUINEA F，et al.The electronic properties of graphene［J］. Rev. Mod. Phys.2009，(81):109.

［13］BOUKHVALOV D W，KATSNELSON M I.Chemical functionalization of graphene with defects［J］.Nano Lett.2008，(8):4373.

［14］MUCCIOLO E R，CASTRO N A H，LEWENKOPF C H.Conductance quantization and transport gaps in disordered graphene nanoribbons［J］.Phys.Rev.B 2009，(79):075407.

［15］EVALDSSON M，ZOZOULENKO I V，et al.Edge－disorder－induced Anderson localization and conduction gap in graphene nanoribbons［J］.Phys.Rev.B 2008，(78):161407(R).

［16］LI T C，LU S P.Quantum conductance of graphene nanoribbons with edge defects［J］.Phys.Rev.B 2008，(77):085408.

［17］ZWIERZYCKI M.Transport properties of rippled graphene ［J］. J. Phys.:Condens. Matter2014，(26):135303.

［18］HAN M Y，ÖZYILMAZ B，et al.Energy band－gap engineering of graphene nanoribbons ［J］.Phys.Rev.Lett.2007，(98):206805.

［19］ZHANG Y，HU J P，et al.Quantum blockade and loop currents in graphene with topological defects［J］.Phys.Rev.B 2008，(78):155413.

［20］LEWENKOPF C H，MUCCIOLO E R.The recursive Green’s function method for grapheme［J］.J.Comput.Electron.2013，(12):203.

［21］DATTA S.Electronic Transport in Mesoscopic Systems［M］.Cambrideg:Cambridge University Press，Cambridge，1995.