Urysohn引理的简单形式与应用

(西南交通大学数学学院，四川 成都 611756)

·基础学科·

Urysohn引理的简单形式与应用

文永明，陈金喜

(西南交通大学数学学院，四川 成都 611756)

建立在一般拓扑空间中存在连续函数使得它的支撑在某个开集内、在开集的某个闭子集上恒为常数的充要条件。同时，在一般拓扑空间中的完美覆盖上建立Urysohn引理，将该定理推广到更加一般的形式，建立子集函数分离的充要条件。文章利用保序定理证明更一般的Urysohn引理，得到集族是完美覆盖的充要条件。同时阐述各种形式的Urysohn引理的联系，得到完美覆盖的重要性质。最后给出Urysohn引理的应用，证明推广的Tietze扩张定理。

拓扑空间；完美覆盖；Urysohn引理；函数分离；Tietze扩张定理

给定拓扑空间X和开集V的闭子集K，在空间X上存在连续函数使得它的支撑包含在V内，在K上恒为常数的充要条件是什么呢？

在拓扑学中，紧集是用覆盖来进行定义的。本文阐述覆盖和连续函数的关系，阐述两个闭集分离的本质。

正规空间中的Urysohn引理用连续函数成功刻画了2个不相交闭集的分离属性，这个引理是非常深刻的,并且有着广泛的应用。它常表述为如下形式。

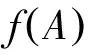
在实分析中,为了在局部紧致的Hausdorff空间中给出Riesz表示定理，需要如下形式的Urysohn引理。

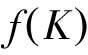
在文献[3]中作者给出了一个推广的Urysohn引理，即下面引理3，它蕴含了引理1和2。

在文献[4]中，作者将Urysohn引理中的函数推广到了函数值是向量的情况。本文将Urysohn引理和Tietze扩张定理进一步推广到一般拓扑空间，得到了更一般的定理2.1及定理3.2。定理2.1蕴含了上述3个引理(Urysohn引理)。本文同时建立了子集函数分离的充要条件(系2)，给出了Urysohn引理的应用。

1 重要概念、引理及符号说明

本文记V为拓扑空间X中的开集族，F为闭集族，设K⊂V⊂X我们记

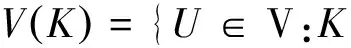
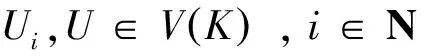
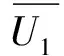
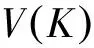
定义1.2 对L⊂W⊂X，记完美覆盖

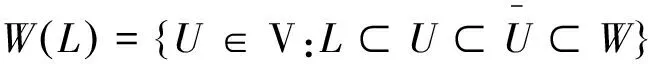
并记

我们称V(K)*W(L)是完美覆盖V(K)与W(L)的乘积。

容易知道完美覆盖有如下性质：

1)若V(K)是完美覆盖，则Kc(Vc)也是完美覆盖；

2)若V(K)，W(L)都是完美覆盖，则V(K)*W(L)也是完美覆盖。

定义1.4[6]集合X中的关系“”称为偏序，如果满足下述条件：

1)对任意x∈X，有xx;

2)若xy且yz，则xz;

3)若xy且yx，则x=y。

定义1.5[7]设集合M，称“”是M上的一个线性序，如果对∀x,y∈M有

1)xy，或yx；

2)若xy且yx，则x=y。

定义1.6[7]若“”是M上的一个线性序，称M是一个链。

定义1.7[7]设(X,)，是两个偏序集合，映射f:X→Y称为保序映射，如果u,v∈X，且u≤v，则有或。

定义1.8[7]设A⊂X，称A是序有界的，如果A关于序既有上界也有下界。集合X是序完备的，如果每一个有上界的非空子集有上确界。

引理1.1[7]设链X，Y，Y是序完备的，f是X的子集X0到Y的保序映射，则f能扩张成X到Y的保序映射的充要条件是f把X中的序有界集映成Y中的序有界集。该引理的证明见文献[7]。

2 主要结果(Urysohn引理的推广)

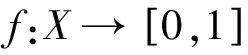
定理2.1 设X为拓扑空间，则V(K)是一个完美覆盖的充要条件是：存在连续函数f:X→[0,1]，使

1)KfV；

证明若K=V=∅，取f=0即可。以下假设K≠∅。

充分性

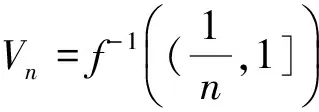
因此V(K)是一个完美覆盖。

必要性

因为V(K)是一个完美覆盖，故存在Vi，U∈V(K)，i∈N使得

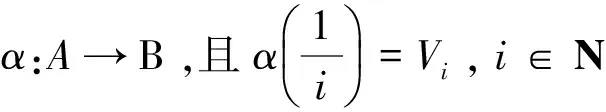
显然，A，B都是链，下面证明B是序完备的。

设B⊂B，假设Vk，k∈N，是B的上界，则V1,V2,…,Vk都是B的上界。

若k是无界的，设Vm∈B，m∈N，则存在k使k≻m，因此Vm⊃Vk，即Vm≻Vk.又Vk≻Vm，故Vk=Vm，易知Vm就是B的上确界。

若k有界，记t是k的最大数，易知，Vt是B的上确界。

由引理1.1，α可扩张成A到B的保序映射，即下式成立：

当ri≻rj时，

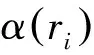
(1)

定义

(2)

并定义

(3)

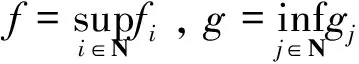
剩下的只需证明f为连续函数，这只要证明f=g即可。

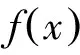
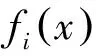
(4)

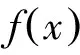
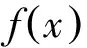
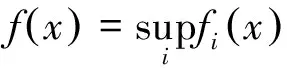
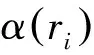
综合1)、2)知f=g，这就完成了定理的证明。

注：定理2.1说明，能在拓扑空间X中建立连续函数使得它的支撑包含在开集V内，在V的闭子集K上恒为常数的充要条件是存在K上的完美覆盖。

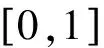
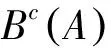
f:X→[0,1]

这样就得到了引理1。

系5 定理2.1蕴含引理3是显然的。

系6 若X为紧致Hausdorff空间，则引理1和2是等价的。

为证明系6，我们还需要如下引理。

引理2.1[8]：在紧致Hausdorff空间中，一个集合是闭集的充分必要条件是它是紧致子集。

证明首先证明引理1蕴含引理2。

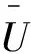
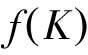
再证明引理2蕴含1。

3 应用

3.1 Tietze扩张定理的推广

引理3.1 设X是拓扑空间，K∈F，V∈V且K⊂V，V(K)是一个完美覆盖,λ是一个正实数，则对于任何一个连续映射

g:K→[-λ,λ]

存在着一个连续映射

使得对∀a∈K有

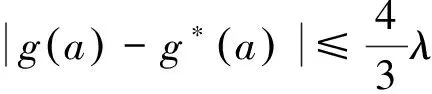
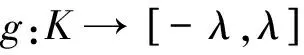
以及

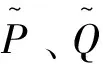
由定理2.1，存在一个连续映射

使得

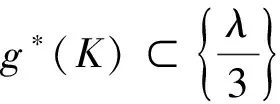
下面验证g*是符合要求的函数。

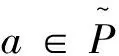
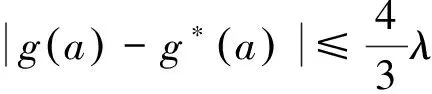
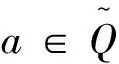
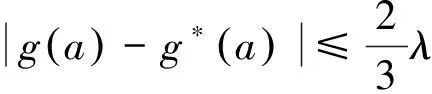
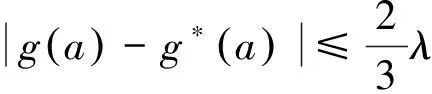
综上，g*符合要求。

这是完美覆盖的重要性质，是文献[8]中引理6.3.3的推广。

类似文献[8]的方法可将Tietze扩张定理推广如下。

定理3.2 (推广的Tietze扩张定理)设X是拓扑空间，[-1,1]是一个闭区间，K∈F，V∈V且K⊂V，则V(K)是完美覆盖的充要条件是：对任何一个连续映射

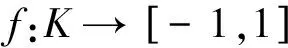
这个定理的必要性的证明，和文献[8]中Tietze扩张定理的必要性的证明是类似的。

证明仅就K,Vc≠∅的情况加以证明。

充分性：定义映射

f:K→[-1,1]，

易见f是一个连续映射。因此存在一个连续映射g：X→[-1,1]是f的扩张。显然当x∈K时g(x)=-1；当x∈Vc时,g(x)=1。由定理2.1，V(K)是完美覆盖。

必要性：设V(K)是X中的一个完美覆盖，令A=K。f:A→[-1,1]是一个连续映射。我们用归纳的方式对于每一个n≥0，定义一个连续映射

对于每个n≥1定义一个连续映射

令f0=f，对于n≻0，假设fn-1已经定义，由引理3.1，存在连续映射

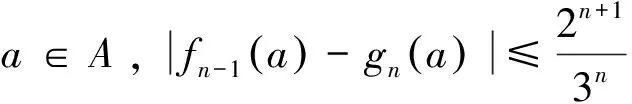
定义映射fn使得对于每一个a∈A有

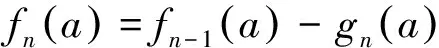
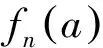
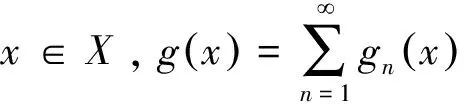
由于对每一个n≥1，有

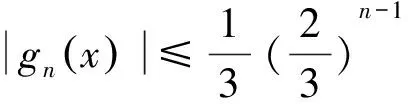
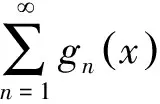
下面验证g满足定理的要求。

首先验证g是f的扩张。设a∈A，对于每一个n≥1，由于

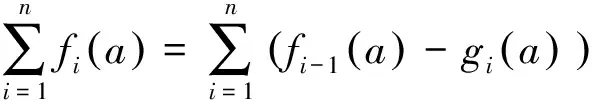
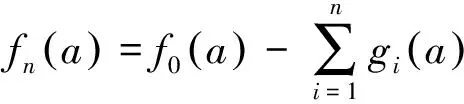
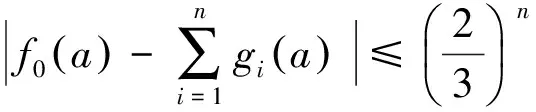
令n→，得。

下面验证g的连续性。

设x∈X，对∀ε≻0，选取整数N≻0使得

对于每一个n=1,2,…N，由于gn是连续的，故存在x的一个领域；设为Un，使得当y∈Un时有

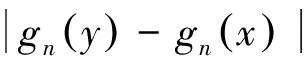
于是当y∈U1∩U2∩…∩UN时，有

这就证明了映射g在点x处连续。由于x是X中的任意一点，所以映射g是X上的连续映射。

3.2在泛函中的应用

假设K是n中的紧集，C(K)是K上的连续函数空间，设g∈C(K)，Λf=∫Kfgdμ。

2)Λ是正线性泛函的充要条件是g≥0。

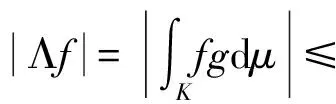
故Λ是有界线性泛函，因而是连续的。

由引理2，存在连续函数u,v∈C(K)使得，FuU，GvV。取ρ=u-v，则有：

2)充分性显然。下面证必要性。

证明V=∅或U(V)=0即可。若V≠∅，且μ(V)>0，

Λv=∫Kvgdμ=∫Vvgdμ=∫Ggdμ+∫VGvgdμ≤∫Ggdμ<0。

矛盾。

陈金喜副教授悉心指导本文的写作并多次审阅全文，对证明中的个别错误给与了指正，对证明的简化和符号的使用提出了有益的建议，谨致谢意。

[1]江辉有.拓扑学[M].北京：机械工业出版社，2013：76.

[2]Rudin W.Real and Complex Analysis[M]．New York:McG raw-Hill,1987：37-39．

[3]丘京辉，周强.一个推广的Urysohn引理[J]．Journal Of Suzhou University Natural Science Edition ，2010,26 (4)：1-2．

[4] 周景新．Urysohn引理与Tietze扩张定理的推广[J].吉林师范学院学报：自然科学版，1999，20(5)：25-27.

[5]朱培勇，雷银彬.拓扑学导论[M].北京：科学出版社，2009：55.

[6]Adriaan C．Zaanen.Introduction To Operator Theory In Riesz Spaces[M] ．Berlin:Springer,1997：1．

[7]Kelly J L.General Topology[M]．New York：Springer-Verlag,1955：13-16．

[8]熊金成．点集拓扑讲义[M].3版．北京：高等教育出版社，2003：172-175，198．

[9]夏道行，吴卓人，严绍宗，等.实变函数论与泛函分析[M].2版.北京：高等教育出版社，2010:109,152.

(编校：叶超)

TheSimpleFormofUrysohnLemmaandItsApplication

WEN Yong-ming，CHEN Jin-xi

(SchoolofMathematics,SouthwestJiaotongUniversity,Chengdu611756China)

We present the sufficient and necessary conditions that there is continuous functions which supports is contained in certain open set and the value is constant in some closed subset of the open set. At the same time, we establish Urysohn lemma in the perfect Cover of general topological space and obtain a more general form of this theorem and construct the sufficient and necessary conditions which the sets are function separared. order preserving theory is utilized to prove a more general Uryshon Lemma and we obtain the sufficient and necessary conditions which a set family is a perfect cover. Then we survey the connection between the various Urysohn’s lemmas and obtain an important property of perfect cover. Finally, we give the application of Urysohn lemma and prove the generalized Tietze expansion theorem.

topological space; perfect-Cover; Urysohn lemma; function separated ；Tietze expansion theorem

2014-05-20

国家自然科学基金NSFC(11301285)；中央高校基本科研业务费创新项目(SWJTU11CX154)

文永明(1985—)，男，硕士研究生，主要研究方向为泛函分析。

O189.1

：A

：1673-159X(2015)04-0052-07

10.3969/j.issn.1673-159X.2015.04.011