基于优先级的物流园区共同配送车辆调度优化研究

(成都市规划设计研究院, 四川 成都 610041)

·新能源汽车与低碳运输·

基于优先级的物流园区共同配送车辆调度优化研究

何 金 海

(成都市规划设计研究院, 四川 成都 610041)

为高效、快速地保证配送任务的完成，实现配送成本最优，在分析物流园区共同配送过程中产生的各种成本的基础上，构建基于优先级的车辆调度优化模型。借鉴交通流分配的思想，引入虚拟距离，提出模型的求解思路和算法。最后，在实际算例中，通过运行Lingo，得出最优车辆调度方案。

物流园区；共同配送；车辆调度；优先级；

物流园区实行共同配送模式，配送量以及配送需求点将显著增加，然而配送需求点空间分布将更加复杂，加之现有道路网络错综复杂，在共同配送模式中仅凭人工经验制定车辆调度方案是难以实现的，尤其是考虑配送的优先级。如何高效、快速地保证配送任务的完成，并且能够实现配送成本最优是当前共同配送模式中面临的挑战。在满足配送需求量限制、车辆装载限制、配送时间限制等一系列限制条件下制定最佳的调度方案，使配送距离最短、配送成本最优、配送服务质量最高是很难实现的[1-2]。对于现有车辆调度的优化研究主要集中在构建惩罚成本和车辆使用成本为目标的，并采取相应的算法进行优化。例如文献[3] 构建油耗费用和固定费用最小的车辆调度模型，并采用云自适应遗传算法进行求解；文献[4]为优化带时间窗的车辆调度计算问题,引入量子进化算法，提出了一种混合量子免疫进化算法；文献[5] 研究了使用蚁群算法优化遗传算法解决物流车辆调度问题。综上所述，现有的研究成果缺乏考虑配送订单的优先级别，因此构建基于优先级的物流园区共同配送车辆调度优化模型，并设计相应的算法是很有必要的。

1 优先级的意义

由于物流园区共同配送中心各企业对配送货物的急迫程度不同，对于优先级较高的客户，在配送过程中需要优先考虑配送，因此在配送中心实施共同配送时需要对其进行分类，并确定各企业各种货物配送的优先顺序，合理分配处理物流配送任务先后顺序。合理制订车辆调度优化方案不仅可以降低物流园区共同配送中心的物流成本，而且可以提高配送服务质量，提升客户满意度，使物流园区共同配送中心达到总体效益最优；因此，配送任务优先级确定在车辆调度优化中起着重要的作用。对于优先级的确定主要与配送任务的配送松弛时间、违约损失成本、配送任务收益、客户配送量以及与客户合作关系等因素相关，具体针对优先级的确定可以采取系统聚类的方法，并引入优先度系数进行确定。

2 模型构建

2.1 模型假设

具体假设如下：

1)物流园区中仅存在一个共同配送中心，车辆从共同配送中心出发，完成所有配送任务后，再回到共同配送中心；2)物流园区共同配送中心的所有配送货物类别大致相同，所需配送车辆类别大致相同，没有特殊车辆需求；3)物流园区共同配送中心所有任务可以混装，可以实现一辆车为多个客户配送，特殊情况除外；4)配送中客户的货物需求量、配送地点、服务时间范围已知，同时配送客户与客户之间的距离已知；5)共同配送中心的车辆充足，能够满足共同配送中心的用车需求；6)不考虑交通事故以及车辆问题等特殊情况对配送服务的影响；7)不考虑配送路网上对车辆量的限制。

2.2 参数变量

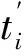
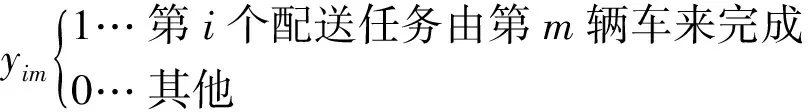
2.3 目标函数

物流园区共同配送中心的配送成本包括配送运输成本、配送延迟或者提前的惩罚成本以及超里程补偿费用成本。

1)配送运输成本。

配送运输成本又包括配送车辆的固定成本和配送车辆的运输成本，固定成本其主要表示如下：

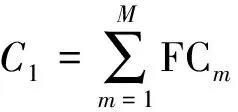
(1)

配送车辆运输成本表示如下：

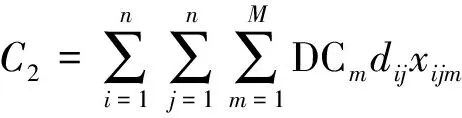
(2)

2)配送惩罚成本。

物流园区共同配送中心的车辆只有在[ETi,LTi]范围之内完成配送任务才能不接受惩罚，若配送提前或者延迟将会得到一定的惩罚，而且惩罚的大小与延迟或提前时间成正比关系，具体函数表达式[6-7]如下：

(3)

为此可以得到物流园区共同配送中心所有任务配送完成后产生的惩罚成本，表达式如下：

(4)

3)超里程补偿费用成本。

超里程补偿费用成本主要是由于单次配送距离过长，因此需要对超正常工作时间以外的驾驶员和装卸人员实施一定的补偿，具体超里程补偿费用成本函数表示如下：

(5)

2.4 模型构建

通过对物流园区共同配送车辆调度问题进行深入分析，可以得到如下基于优先级的物流园区共同配送中心车辆调度优化模型：

(6)

s.t.

1)车辆容量限制。

(7)

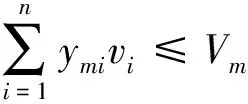
(8)

2)车辆运行限制。

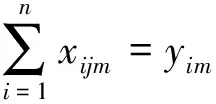
(9)

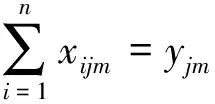
(10)

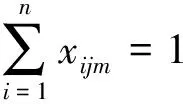
(11)

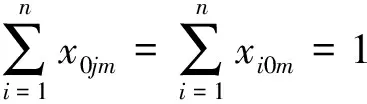
(12)

3)车辆时间限制。

tij=dij/v，

(13)

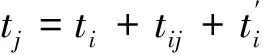
(14)

t0=0，

(15)

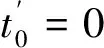
(16)

4)其他限制。

xijm=0或1，i,j=1,2,3,…,n,

m=1,2,3,…,M。

(17)

yim=0或1,i=1,2,3,…,n,

m=1,2,3,…,M。

(18)

目标函数(6)表示车辆的总成本最优，包括车辆固定成本、车辆运行成本、惩罚成本以及超里程补偿费用成本；约束条件(7)表示每辆车装载的货物重量不能超过其最大载重；约束条件(8)表示每辆车装载的货物体积不能超过其最大载重体积；约束条件(9)、(10)、(11)表示每个客户只由一辆车服务且只服务一次；约束条件(12)表示每辆配送车辆都是从物流园区共同配送中心出发然后又回到共同配送中心；约束条件(13)表示从客户i至客户j车辆所花费的时间；约束条件(14)表示到达配送客户j的时间等于到达配送客户i的时间加上配送客户i所花费的时间和配送客户i至客户j车辆所花费的时间；约束条件(15)、(16)表示配送车辆从配送中心出发和抵达时间为0；约束条件(17)、(18)表示决策变量的值。

3 模型求解思路

由于物流园区共同配送中心对所有的配送任务进行分级处理，得到不同级别的配送任务。对于配送任务级别较高的则需要保证能够按时送达，而对于一般的配送任务则保证以企业利益最大化为目标，对配送任务实施配送。为此，在配送过程中借鉴交通流分配的思想，引入虚拟距离的概念进行求解，对于配送任务等级比较高的则采取优先配送，对于配送任务优先级比较低的则可以相应地延迟配送，最终使整体配送效率和效益达到最优。

设物流园区共同配送中心有n个配送任务，其中物流园区共同配送中心用0表示，则各配送任务之间的距离表示如下：

由于在车辆调度优化过程中假设i到j的距离等于j到i的距离，即dij=dji，假设第i个配送任务的配送级别为τi，其中τi∈[1，2，3，4]，车辆配送每个配送级别对应一个虚拟距离系数ξi，其中ξi∈[0,1]，ξ0=1，为此i到j的虚拟距离表示如下：

(19)

(20)

车辆从i到j的虚拟距离需要乘以j的优先级系数，车辆从j到i的虚拟距离需要乘以i的优先级系数，所以i到j的虚拟距离大小不同。根据前面的分析，可以将整个配送网络的虚拟距离矩阵表示如下：

对于车辆调度优化研究大多采用节约费用法[2,8]，因此在基于优先级的情况下，原有求解费用节约值时需要对其修正，即在原有的费用节约值基础上需采用虚拟距离的费用节约值，其他的费用节约值依旧采取原有的实际距离进行计算。

4 算例分析

4.1 基础数据

假设选取某物流园区10组配送数据进行验证，具体的数据如表1所示。

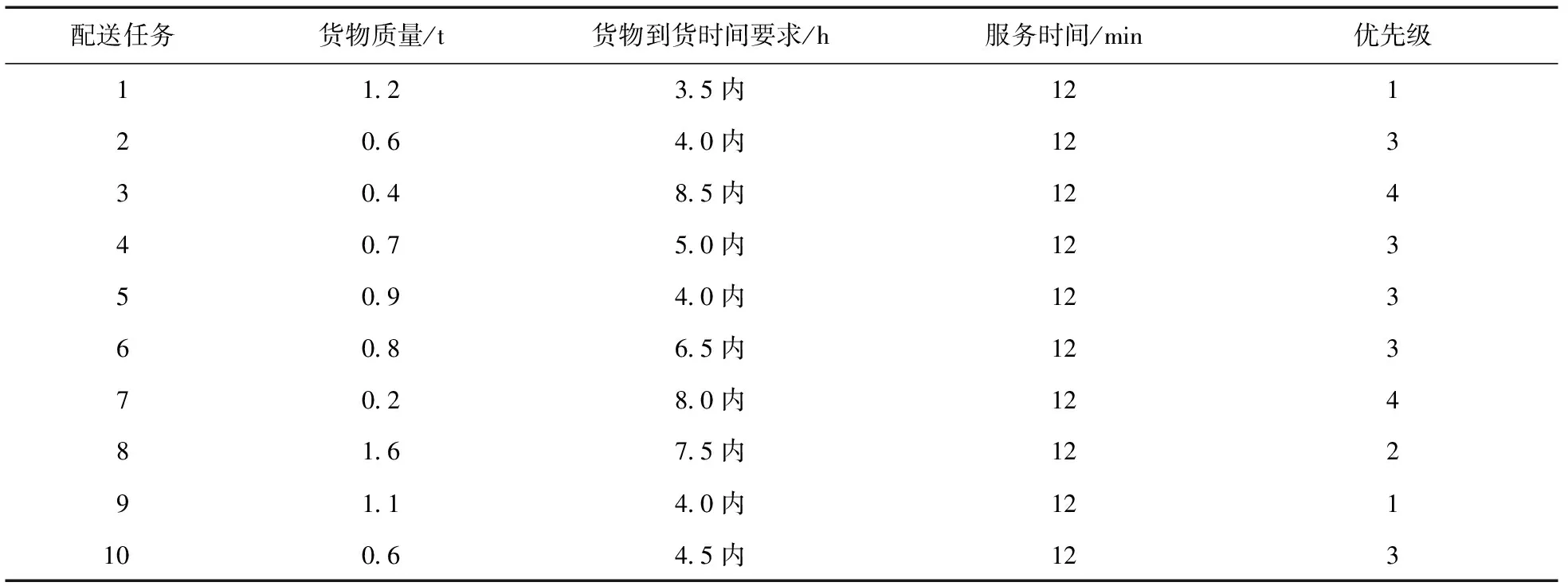
表1 配送任务基础数据

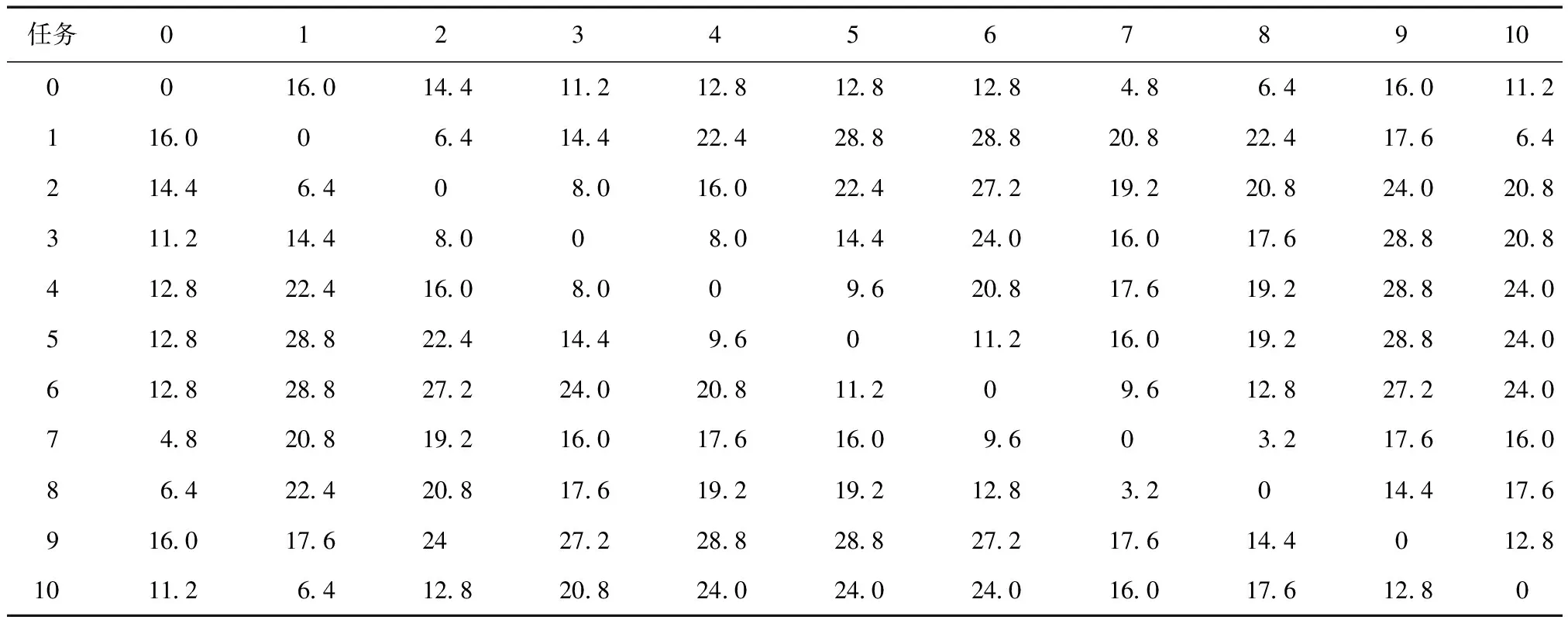
表2 配送任务之间的距离

4.2 虚拟距离计算

在进行虚拟距离计算时，虚拟距离系数ξi的取值为ξ0=1.0，ξ1=0.4，ξ2=0.6，ξ3=0.8，ξ4=1.0，为此物流园区共同配送中心配送任务之间的虚拟距离如表3所示。

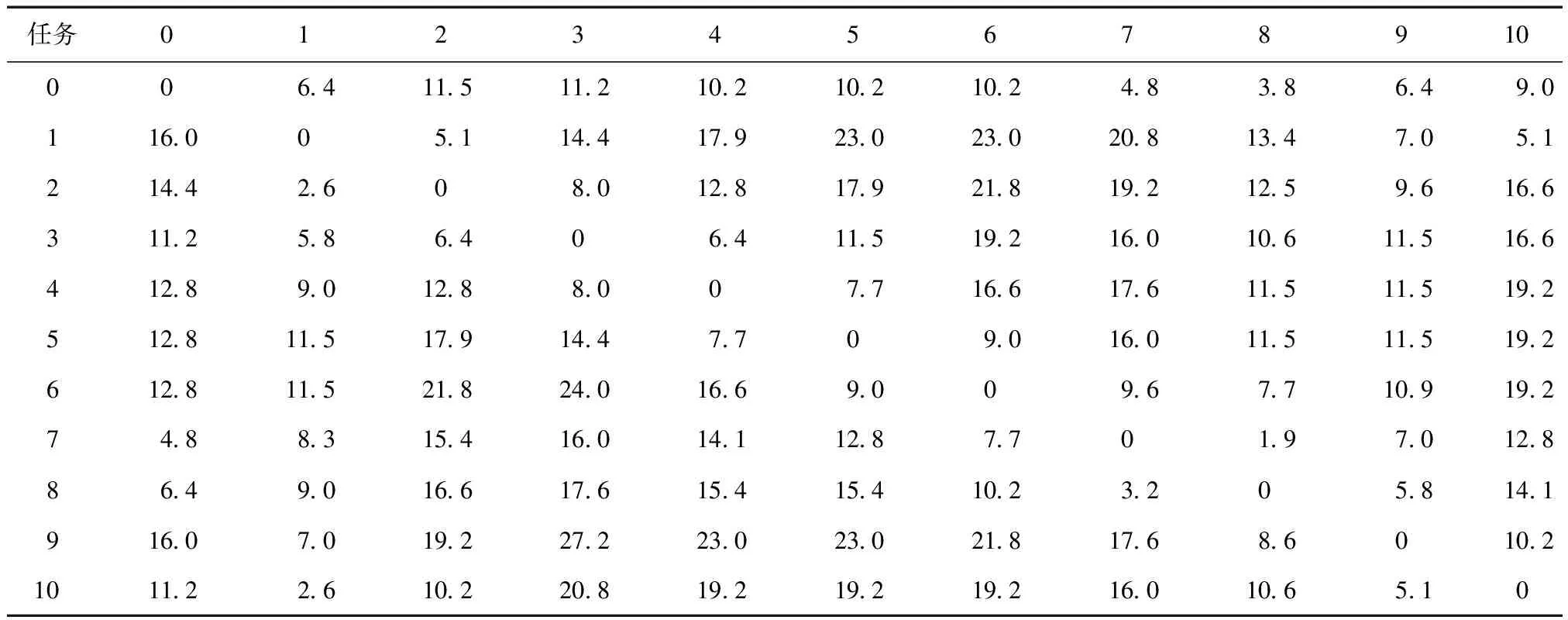
表3 配送任务之间的虚拟距离

4.3 模型求解

将10组配送任务的具体数据、虚拟距离以及模型中所需要的具体参数代入模型中，选取固定成本为160元，单位成本为5元，每辆车限重为3 t，车辆运行速度为40 km/h，时间惩罚成本系数为500，车辆超里程惩罚成本系数为100，并且将其具体模型写入程序中，经运行程序可以得到以下的运行结果。

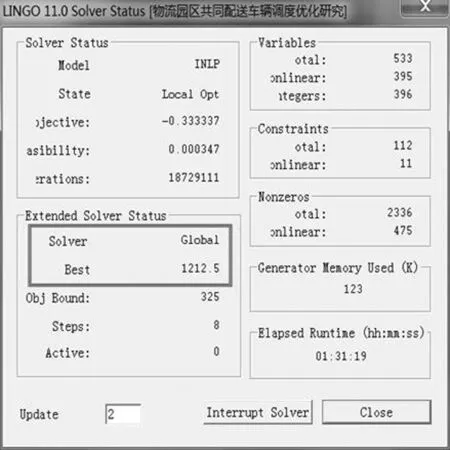
图1 LINGO运行结果

通过模型求解得到基于优先级的物流园区共同配送车辆调度优化模型的最优成本为1 212.5元，其中固定成本为480元，变动成本为732.5元，时间惩罚成本为0元，超里程惩罚成本为0元，所有的配送任务都在满足配送需求的前提下完成配送任务。

通过程序结果可以得到该10组配送任务需要3辆车进行配送，同时可以得到每辆车的配送路线以及配送任务的顺序等结果，具体的车辆调度优化方案见表1所示。

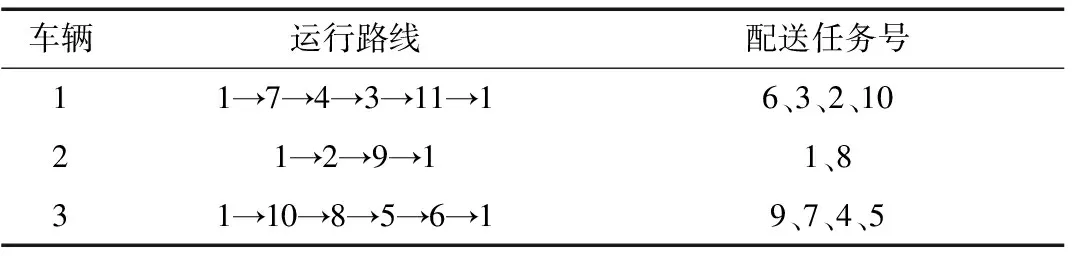
表4 物流园区共同配送车辆调度优化结果

5 结束语

本文在构建物流园区共同配送中心车辆调度优化模型中，不仅考虑了时间惩罚成本和超里程惩罚成本，同时还考虑物流园区共同配送中心的配送任务优先级别，确定不同配送任务的轻重缓急。同时，借鉴交通流分配的思想，采用虚拟距离系数的方法，得到不同配送任务之间的虚拟距离。该方法将有利于企业在配送过程中看清任务的轻重缓急，在企业遇到相应的问题时，能够及时采取相应的措施来满足客户的配送服务要求和服务质量，保证共同配送中心的信誉和企业的运作效率。

[1]李军,郭耀煌.车辆优化调度理论与方法[M].北京：中国物资出版社,2001： 10-11.

[2]童岱. 小件货物运送车辆调度优化[J].西华大学学报：自然科学版， 2005, 24(5):43-44.

[3]蹇洁,王旭,葛显龙. 云自适应遗传算法有能力约束的车辆调度优化[J].重庆大学学报： 2013, 36(8):40-46.

[4]任伟. 基于量子免疫算法的车辆调度问题优化[J]. 计算机科学，2013,40(5):233-270.

[5]邵丽丽. 蚁群优化自适应遗传算法物流车辆调度实现[J].计算机测量与控制，2012,20(5):1423-1425.

[6]赵鲁华.城市配送中心车辆调度优化研究[D]. 长春：吉林大学,2005.

[7]蔡珊珊.需求驱动下的城市配送车辆动态配置研究[D].北京：北京工商大学，2011.

[8]刘琳.冷链物流配送优化路径模型及控制算法[D].烟台：烟台大学，2012.

(编校：夏书林)

ResearchonVehicleSchedulingOptimizationofJointDistributioninLogisticsParkbasedonPriority

HE Jin-hai

(ChengduInstituteofPlanning&Design,Chengdu610041China)

In order to deliver efficiently and rapidly with minimum cost, various costs generated during the joint distribution of Logistics Park are analyzed and the optimization model on vehicle scheduling is set up according to priority. The solution and algorithm of the model are put forward based on the distribution theory of traffic flow and the virtual distance. They are demonstrated in Lingo environment and the optimum vehicle scheduling is obtained.

logistics park; Joint distribution; Vehicle scheduling; priority;

2014-10-04

何金海(1988—)，男，硕士研究生，主要研究方向为物流园区规划与共同配送。

F259.2

：A

：1673-159X(2015)04-0071-05

10.3969/j.issn.1673-159X.2015.04.014