擦窗机伸缩臂接触应力分析

立 威，黄日龙，谢家学，田常录

（1.江南大学 机械工程学院，江苏 无锡 214112；2.无锡吊蓝机械制造有限公司，江苏 无锡 214125)

擦窗机伸缩臂接触应力分析

立 威1，黄日龙1，谢家学2，田常录1

（1.江南大学 机械工程学院，江苏 无锡 214112；2.无锡吊蓝机械制造有限公司，江苏 无锡 214125)

[摘 要]为了解擦窗机伸缩臂与滚轮接触部位的应力变化，基于Hertz接触理论对擦窗机的伸缩臂与滚轮进行了接触分析，导出了接触应力函数以及滚轮尺寸设计的公式，并通过软件模拟出应力变化与接触位置以及材料泊松比的关系变化曲线。针对无锡宝能大厦CWGS250型轨道式擦窗机进行理论分析，计算出实际受力，并进行相应的有限元计算，对两种方法得出的结果进行分析比较。结果表明本文的理论方法合理可靠，可以作为擦窗机设计的理论计算方法。

[关键词]擦窗机伸缩臂；赫兹接触理论；应力分量；滚轮尺寸

伸缩臂是擦窗机工作时的主要承载结构。进行伸缩臂设计时，需要确定载荷值和载荷组合，需对伸缩臂上作用的载荷进行研究。其主吊臂与伸缩臂之间通过滚轮连接，该接触为线面接触，易产生高应力，如图1所示。

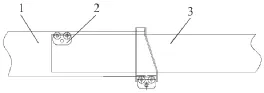
图1 擦窗机伸缩臂结构示意图

端部载荷过大可能会造成与滚轮接触的伸缩臂底部钢板局部压缩变形，是吊臂结构的一个薄弱部位，因此本文将以赫兹接触理论为基础，试导出擦窗机的滚轮与伸缩臂接触处的应力场。

1 伸缩臂与滚轮接触部位理论分析

1.1 接触部位的应力推导

赫兹接触理论假设接触表面的压应力分布为半椭圆体，且有如下结论：线接触物体受力后其接触表面为矩形。在应变最大的接触表面中心压应力最大。根据接触表面压应力分布规律求得表面接触压力所组成的合力应等于外加载荷[1]。

由赫兹接触理论得，滚轮与伸缩臂发生弹性接触时，由于接触部位为线面接触，所以受力后的接触表面为矩形，且该矩形接触面的压应力分布是一个半椭圆体[2]，如图2所示。设矩形接触表面的长度为L，宽度为2b。

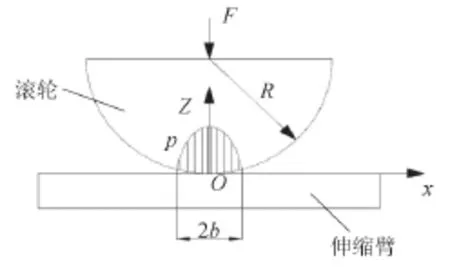
图2 伸缩臂与滚轮接触图

设F为滚轮所受外部载荷，R为滚轮半径。

由于接触宽度2b＜＜R，因而接触表面上的任一点都可按弹性力学中半无限平面进行分析[3]。由一般圆柱体与平面接触公式[4]

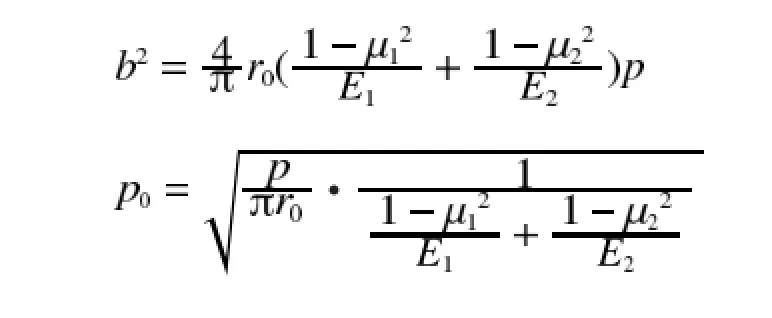
则滚轮与伸缩臂接触部位的b和b0为

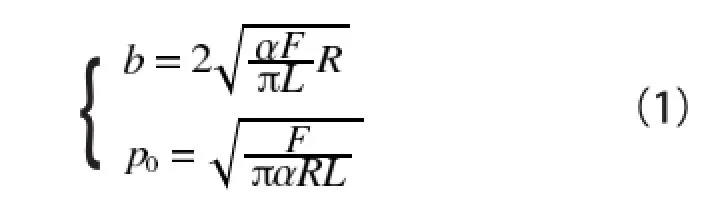
由式(1)可见：接触面半宽度b与F、R的平方根成正比，与L的平方根成反比；最大接触应力P0与F的平方根成正比，与R、L的平方根成反比。因而在设计过程中，设计人员可根据实际情况选择相应的尺寸参数，确保接触面的触面宽度与最大接触应力在设计要求之内。

接触表面在外部载荷F的作用下所产生的应力，可利用布辛奈斯克应力公式[3]算出应力分量，再采用叠加原理求出应力分布中心z轴上的正应力和剪应力分别为

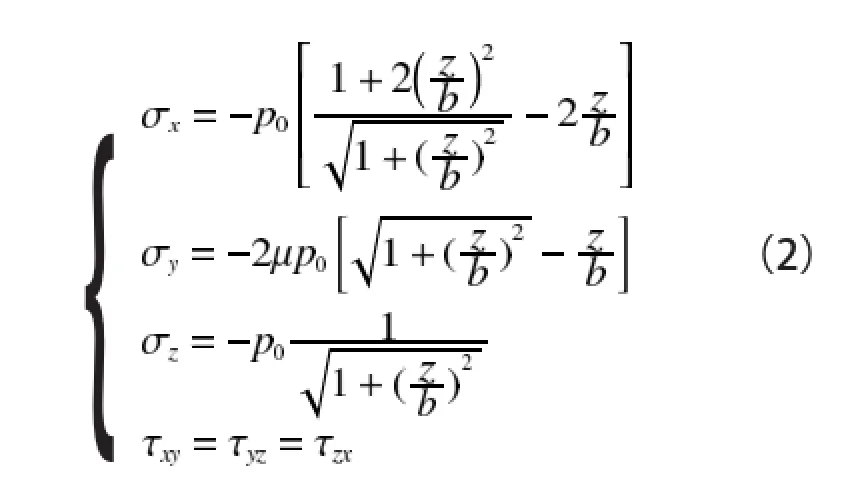
由式(2)可知σx，σy，σz为主应力，则最大剪应力为

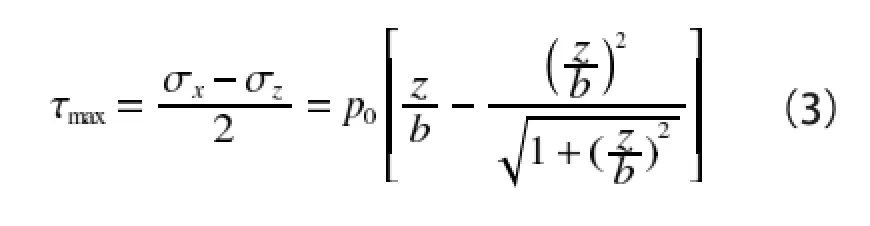
其中z为接触点到滚轮中心对称面Z轴的距离，应力分量σx，σy，σz均处于受压状态，且随着z值的变大而迅速减小。

1.2 接触部位等效应力分析

根据第四强度准则(形状改变比能理论)[5]，可得z轴上点的von Mises 等效应力为

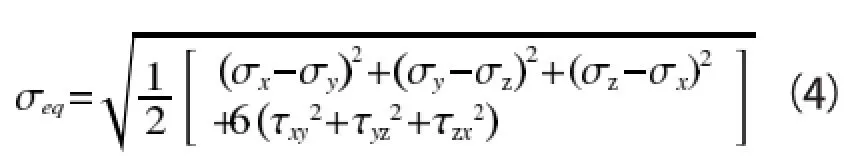
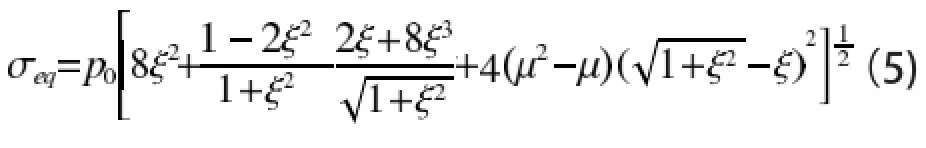
图3为由式(5)得到的等效应力σeq/po随接触点位置ξ、材料泊松比μ的变化情况。

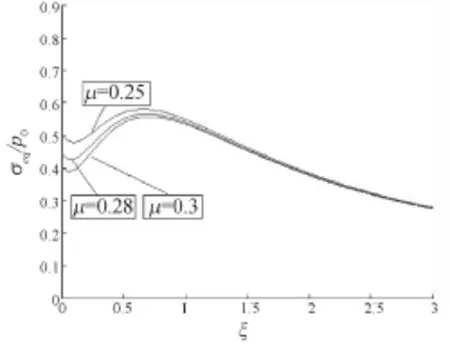
图3 等效应力σeq/po与接触点位置ξ以及泊松比μ关系

令k0=σeq/p0，从上图可以得出，随着材料泊松比μ的增大，k0值随之减小，且最大值发生位置由接触表面中心向接触区域内部移动。由图得,当μ=0.25时，k0在ξ=0.6513处取得最大值。☒μ=0.28时，最大值于ξ=0.6721处。μ=0.3时，最大值出现在ξ=0.7042处。

图4为伸缩臂与滚轮接触部位z轴上最大等效应力σeqmax/p0与材料泊松比μ的关系图[5]。从图3与图4中可以看出，在μ=0.1938时，最大等效应力k0max的出现位置开始变化。当μ＜0.1938时，k0max发生在接触区域表面，当μ＞0.1938时，k0max于接触区域内部产生。

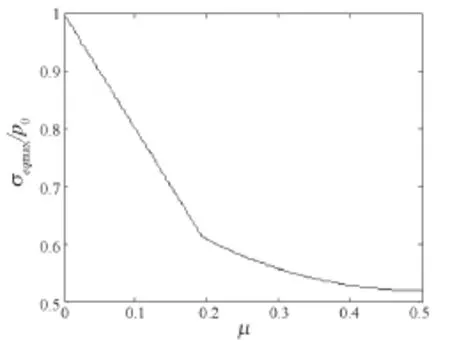
图4 等效应力σeqmax/po与材料泊松比μ的关系

当设计擦窗机时，可根据图3得到相对应于滚轮材料泊松比μ的k0值，令σeqmax等于材料的屈服应力σs，代入式k0=σeqmax/p0即可得出接触部位的最大临界接触应力p0max，再将p0max代入式(1)中，并根据滚轮实际受力情况，就可得出滚轮半径与宽度的关系公式

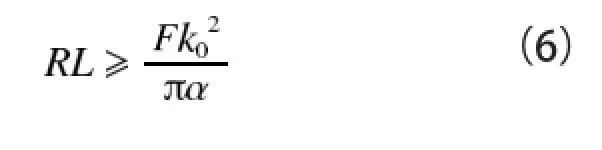
式(6)可作为擦窗机接触部位滚轮尺寸的初步设计依据。

1.3 滚轮与伸缩臂接触部位的受力分析

取雄宇重工公司的CWGS250型轨道式擦窗机产品作为模型，分析接触部位应力情况，如图5所示。

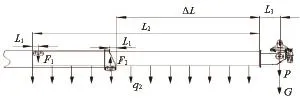
图5 伸缩臂受力示意图

其中，L1=0.15m，L2=8.1m，L3=1m，ΔL=5.2m，q2=657.5N/m，G=1 000N，p=2 500N，滚轮尺寸为：半径R＝0.085m，宽度L＝0.04m。则由力矩平衡得

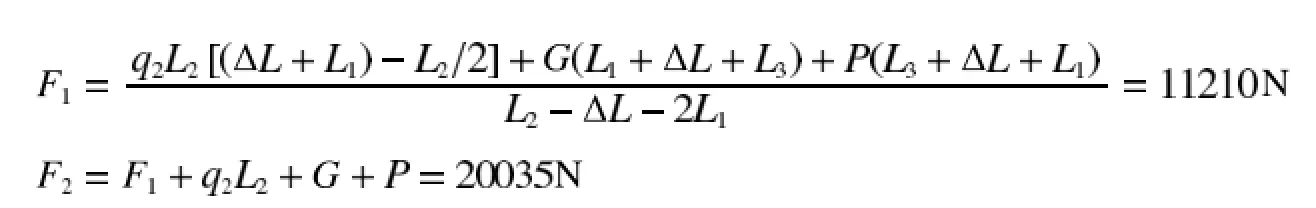
因伸缩臂上支点处安装有一个滚轮，下支点处安装有两个滚轮，故上下支点处滚轮分别受压力为F1′=F1/2=5605N，F2′=F2/4=5005N。

取受力较大的支点，即选取上支点处的接触部位作为对象进行分析，将所受压力代入式(1)中，得b=0.275mm，p0=245.65MPa。

由式（5）得von Mises等效应力为

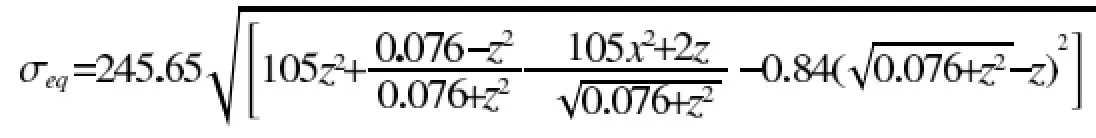
则由上式可得出该型号擦窗机的滚轮与伸缩臂接触部位σeq随Z轴坐标的变化曲线。

从图6可看出，滚轮在z=0.3542mm取得最大等效应力为σeqmax=323.38MPa。由于该型号擦窗机滚轮所用材料为45#钢，故屈服强度σs≥355MPa，则滚轮满足设计要求。

2 伸缩臂接触有限元分析

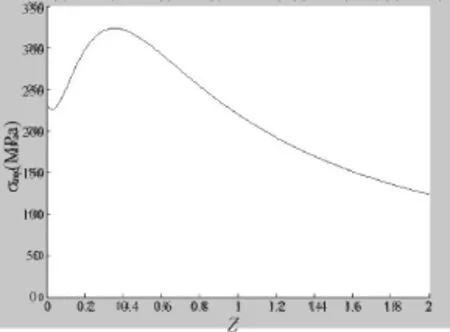
图6 接触部位σeq与Z的关系图

为了对比分析，利用ANSYS有限元软件对该型号擦窗机的滚轮与伸缩臂接触部位进行应力分析[6]。因接触模型具有对称性，为降低计算量，将接触模型简化为1/4模型，采用SOLID185单元模拟滚轮与伸缩臂[7]，设置材料参数为：弹性模量E=210GPa，泊松比μ=0.3。根据1.3节中的计算结果建立有限元模型（伸缩臂用长方体代替），如图7所示。

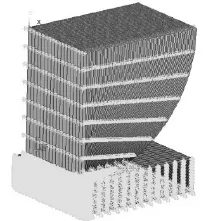
图7 伸缩臂与滚轮接触的有限元模型

据有限元法[8]可发现接触部位最大接触等效应力σeqmax的发生位置在接触区域内部而非表面，与1.3节所得结论相同。

拟合接触区域中心Z轴上各个节点的等效应力值，即可得到Z轴上的等效应力分布曲线图8。从图中可看出，最大等效应力为σeqmax=305.79MPa。

对比有限元法模拟图8与理论法所得等效应力图6，可以看出有限元法获得的曲线与理论法获得的曲线趋势基本一致，二者无论是在σeqmax出现的位置还是数值上都很相近。

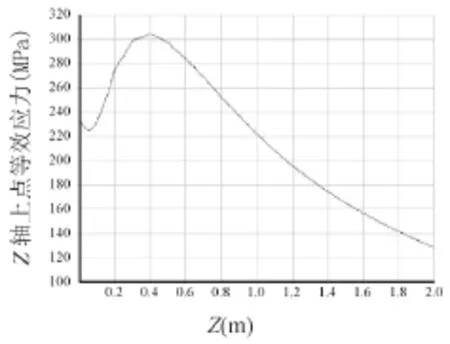
图8 接触区域中心处Z轴上等效应力分布曲线

3 讨论与结论

1）利用赫兹接触理论以及有限元法对接触部位分别进行理论计算以及模拟计算，数值结果基本吻合，但存在一定的误差。总结原因有如下3点：①计算方法不同：赫兹接触理论的前提条件是小变形，而有限元法是在大变形条件下求解；②模型存在差别：理论模型基于半无限平面，而有限元模型基于有限平面；③有限元法在多次迭代过程后会产生一定的累计误差。

2）对比有限元法与理论计算所得最大等效应力值，理论解大于有限元数值解，误差为5.76%，因而本文结果可靠偏保守，可以作为擦窗机设计的理论计算方法。

[参考文献]

[1] 黄 炎．工程弹性力学[M]．北京：清华大学出版社．1982．

[2] K.L.Johnson．接触力学[M]．北京：高等教育出版社，1992．

[3] 杨伯源，张义同．工程弹塑性力学[M]．北京：机械工业出版社，2003．

[4] 李章政．弹性力学[M]．北京：中国电力出版社，2011．

[5] 刘士光，张 涛．弹塑性力学基础理论[M]．武汉：华中科技大学出版社，2008．

[6] 李 群．轮轨滚动接触过程的有限元分析[D]．秦皇岛：燕山大学，2007．

[7] 张洪才．ANSYS14．0理论解析与工程应用实例[M]．北京：机械工业出版社，2013．

[8] 杜向阳．伸缩臂式高空作业平台工作装置的动态仿真与优化[D]．西安：长安大学，2012．

（编辑 贾泽辉）

Product.Technology 产品·技术

Contact stress analysis of the gondola telescopic boom and wheel

LI Wei, HUANG Ri-long, XIE Jia-xue, TIAN Chang-lu

［中图分类号］TU976+.42

［文献标识码］B

［文章编号］1001-1366(2015)06-0045-03

［收稿日期］2015-03-26