基于数学史的加权平均数的教学实践
2015-07-13吴骏��朱维宗
吴骏��+朱维宗
初中统计教学中的平均数主要指加权平均数,是对算术平均数的进一步深化.在算术平均数的计算中,所有数据都是按照等比例去计算,而对于加权平均数,一组数据中各个数据的重要程度未必相同.学生虽然在小学已经学过算术平均数,但从算术平均数到加权平均数经历了一个很大的跨越,其实学生并未做好这方面的准备,因此加权平均数的学习并非容易.一些学者对加权平均数的教学进行了研究,但从历史发生视角的却很少见.为加强学生对加权平均数的理解,本文借助数学史,结合人教社教材加权平均数的内容,从加权平均数的引入、组中值的探究和用样本平均数估计总体平均数三个方面,设计了相关的教学案例,以弥补原教学的不足,并在八年级付诸教学实践.1加权平均数的引入
教材分析教材中先利用数据的不等比例和百分比引入加权平均数的概念,再把频数分布中的平均数看作加权平均数.事实上,学生对后者容易理解,而对前者中的“权”感知困难.鉴于此,可从数学史的视角审视加权平均数的引入.1962年夏天,美国哈姆林大学统计学家Varberg教授为中学数学教师作了两个关于统计历史发展的演讲.他在第一个演讲中,就是把测量数据用线条图来表示,直观地表达了数据的个数,从而较为简单地计算出这组数据的平均数,这就是加权平均数的计算公式.下面的案例结合八年级学生的实际情况,对Varberg的例子进行适当改编,从频数分布中算术平均数的计算引入加权平均数.
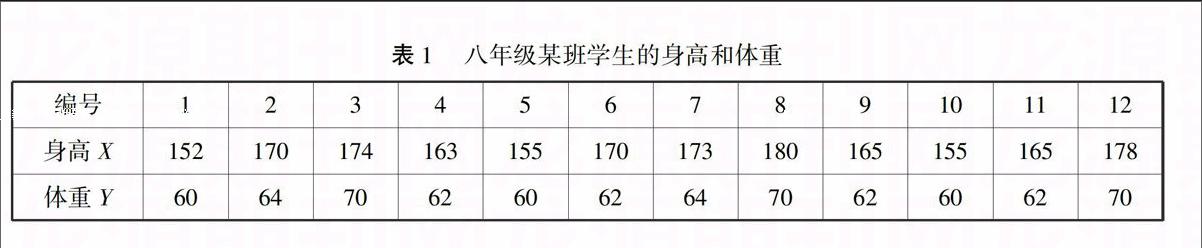
教学案例1测量八年级某班学生的身高和体重,下表(表1)是12个学生的数据表,其中身高X以公分为单位,体重Y以公斤为单位.
英国人普莱菲(William Playfair,1759—1823)被公认为将图形表征思想介绍到统计学的第一人.他关于经济学的著作中,大多采用图形如直方图、条形图等表征数据.为了更好地描述这两组数据,教师在课堂上引导学生用图形呈现这些数据.
教师:如何直观地描述这两组数据呢?
学生:采用作图的方法.
教师:我们目前学过作图的方法有哪些?
学生:折线图、扇形图、条形图、直方图.
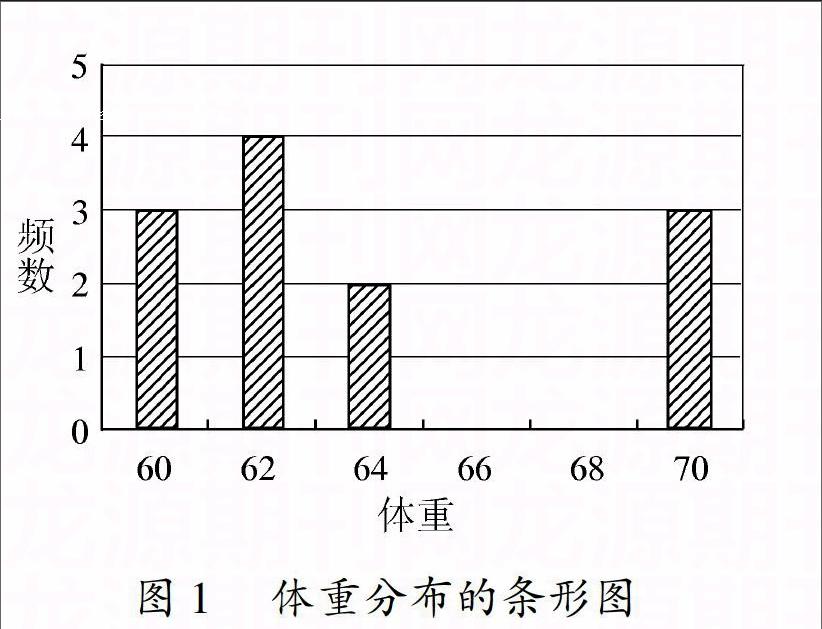
在这个问题中,用频数分布图就能很清楚地把数据表示出来.图1是体重Y数据的频数分布条形图.身高X的频数分布图也可以类似表示.图1体重分布的条形图
虽然这类图形能帮助我们从直觉上感知这些数据,但是如果要对这些数据更进一步了解,则需要用某些统计量来分析它们,其中最重要的是平均数.实际上,平均数的起源可追溯至古希腊.亚里斯多德(Aristotle,384—322 BC)给出了平均数的几何定义:a和c中间的数b称为算术平均数当且仅当b-a=c-b,用现代术语表述即为:b=a+c2.在教学中,教师引导学生用平均数来反映数据的集中趋势.
教师:你能求出这组数据的平均数吗?
学生:把这些数据全部相加,再除以它们的个数.
即这组数据的算术平均数为:
(60+64+70+62+60+62+64+70+62+60+62+70)/12=63.83,
为了理解这个概念的重要意义,教师引导学生观察图1:
教师:观察上述体重分布的条形图,你能发现更简单的方法吗?
学生:不必把每个数据一一相加,只要把相同的体重乘以频数就行.
于是,这个公式写成更为简明的形式:
60×3+62×4+64×2+70×33+4+2+3=63.83,
一般地,n个观测值xi的平均数可以表示为:
=1n(x1f1+x2f2+x3f3+…+xkfk),
其中xi代表变量X的数值,fi是xi出现的次数,称为比例或比重,且f1+f2+…+fk=n.
这就是频数分布中平均数的计算,有了该案例之后,再讲教材中的例题,最后才引入加权平均数的概念.该案例虽然还没有直接建立加权平均数的概念,但为加权平均数中“权”的引入作了一个很好的铺垫.
设计说明该案例的设计考虑到历史现象、教材顺序、逻辑结构和学生认知几个方面之间的关系,先引出频数分布的平均数,再给出不等比例和百分比数据的加权平均数,自然呈现知识的发生过程,符合学生的认知发展规律,使算术平均数到加权平均数的过渡更为顺畅.2组中值的探究
教材分析教材以公共汽车载客量为探究问题,直接给出了组中值的概念及其计算,但并没有交待求组中值的原因,也没有说明为什么组中值可以作为各组数据的平均代表,因此,组中值的出现显得很突然,学生难以理解.事实上,从历史的视角来看,算术平均数的前概念是中点值,即两个极端值的算术平均数.中点值在9世纪至11世纪阿拉伯人的天文、冶金和航海中有广泛的应用.托勒密(Ptolemy,100—170)在《天文学大成》中指出:取最大值和最小值的平均数是一条法则.这样做的目的是为了降低观察值的误差,所得的结果介于最大值和最小值之间.从现代的观点来看,中点值不是一个很有用的平均数,因为它对极端值太敏感.学生在开始学习平均数时,可能会把中点值的计算作为求平均数的原始方法.因此,中点值的探究是平均数教学的基础.为此,教师可以借助以下教学案例来探究如何估计两个数的平均值.
教学案例2公元前400年,在伯罗奔尼撒人战争中,Homer为了了解对方的兵力,进行了实地考察,发现对方运载士兵的船只共有1200条,这些船只大小不等,最大的船能容纳120名士兵,最小的船能容纳50名士兵,试估计对方的人数.
学生对这个问题的回答有3种情形:
(1)1200×120+1200×501200;
(2)1200×120+1200×50120+50;
(3)1200×(120+50)2.
从这些回答可以看出,在不同背景下,学生对加权平均数的理解存在偏差.在第一种方法中,学生没有理解加权平均数公式中的频数,误认为1200;第二种方法中,学生没有理解权重,机械套用加权平均数公式;第三种方法利用中点值估计出每条船上的平均人数,从而得出所有船只能容纳的人数.
当学生认识到中点值可以作为一组数据的估计值后,在探究公共汽车载客量的问题上就容易多了.
教师:以第一小组为例,它表示什么意思?
学生:载客量在1≤x<21之间的班次出现了3次.
教师:能够确定这个小组的载客量吗?
学生:不能,这个区间只有范围,而没有具体的数字.
教师:能否用一个数表示出它的估计值,作为该小组载客量的代表.(小组开始讨论)
教师:如何选出这个代表?
学生:求平均数.
教师:如何求平均数?
学生:取这个区间两个端点的平均数.
教师:能不能用中位数?
学生:不能,因为人数不确定,无法找到中位数.
教师:能不能用众数?
学生:不能,因为无法确定出现最多的人数.
教师:在第一组中,由于3个班次的人数不确定,只是介于1≤x<21之间,因此无法求出该组数据的中位数和众数.可以用1+212作为这个小组载客量的估计值,称为组中值,这样就解决了该小组平均载客量的问题.
设计说明以战争问题为背景,引导学生自己发现组中值产生的过程,从而把组中值作为该组数据的代表,过渡自然易于接受.从上课效果来看,学生很喜欢此问题的设计.这也表明,通过探究获得的知识,比教师讲授更容易掌握.3用样本平均数估计总体平均数的思想
教材分析教材在本章引言中指出,用样本估计总体是统计的基本思想.当所要考察的总体中个体很多或者对考察对象带有破坏性时,统计学中常常通过样本估计总体的方法来了解总体.这就意味着,用样本估计总体的基础是抽样.因此,在该部分的教学中,学生首先需要具有一定的抽样思想,才能用样本推断总体.下面介绍一个教学案例——货币检查箱试验,随机抽样的思想隐含在该案例中.
教学案例3现在的硬币是由比较便宜的材料做成的,与以前的做法已经大不一样了.很久以前,硬币是由黄金和银子做成的,与黄金和银子具有相同的价值.在12-18世纪,英国皇家制币厂在制造硬币时,制造商就需要对硬币的重量进行检查:这些硬币既不能使用太多也不能使用太少的黄金和银子,即需要检验硬币的重量是否达到规定的标准.但由于硬币太多,把每一枚硬币都称重是不可能.请你为国王设计一个如何检验这些硬币重量的方案,并作出解释.
教师:如何检验这些硬币的质量?
学生:抽取10个硬币,称出它们的重量,计算出平均数,检验是否达到规定的标准.
教学实践表明,学生提出抽取10个、20个、30个硬币不等,这可能是学生的一种抽样直觉.遗憾的是,教师没有追问学生这些硬币是如何选择的,因而随机的思想没有体现出来.
事实上,当时的英国皇家制币厂是这样来检验硬币重量的:他们做了一个货币检查箱,每天把生产的硬币随机拿出一枚放到货币检查箱里.一个月后,打开货币检查箱,取出硬币,把这些硬币称重,最后计算出一枚硬币的平均重量,看是否达到规定的标准,由此来检验这个月生产硬币是否达到规定的标准.如果事实证明这些硬币的重量达到规定的标准,则国王就会举办晚宴来庆贺;否则,制币者就会受到国王的惩罚.
设计说明这个历史现象表明,平均数的学习与抽样问题紧密相连,这也是学生学习平均数的困难之一,不过,有了这样的联系,也可以从学生学习平均数的过程中进行抽样问题的教学.该案例利用历史故事吸引学生的注意力,帮助学生再现抽样方法,说明抽样思想产生的必要性.在抽样的基础之上,学生就能更好地理解用样本平均数估计总体平均数的思想.
Fauvel和van Maanen指出:“数学史引入数学教学,其目的是更好地促进学生的学习.因此,数学史引入数学教学的研究乃是数学教学研究的重要组成部分.”上述三个教学案例的教学实践表明,在数学教学中引入数学史,不是为了教历史,而是帮助教师更好地理解教材,了解学生的认知障碍,从而有效地改进教师的教学和促进学生的学习.
参考文献
[1]Pollatsek,A.,Lima,S.,& Well, A. D. Concept or computation: Students understan ding of the mean[J]. Educational Studies in Mathematics, 1981,12(2):191-204.
[2]梁绍君.“算术平均数”概念的四个理解水平及测试结果[J].数学教育学报, 2006,15(3):35-37.
[3]李建勋.平均数教案设计[J].HPM通讯, 2013(10):4-16.
[4]隋淑春,林建明.“加权平均数”情境式教学课例研究[J].中国数学教育, 2012(3):28-31.
[5]Varberg, D. E. The development of modern statistics[J]. The Mathematics Teacher, 1963,(4): 252-257.
[6]吴骏,黄青云.基于数学史的平均数、中位数和众数的理解[J].数学通报,2013,52(11):16-21.
[7]Bakker, A. Design research in statistics education—On symbolizing and computer tools[D]. Ph.D. thesis, The Freudenthal Inistitute, Utrecht, 2004.
[8]Fauvel, J., & van Maanen, J. History in mathematics education[C]. Dordrecht: Kluwer Academic Publishers, 2000.
