除草用四足机器人稳定性的判定与分析

张皓然，戈振扬，于英杰，陈林，丁巍，卢衷正

(昆明理工大学现代农业工程学院，云南 昆明 650500)

除草机器人代替人工除草，能减轻劳动强度，减少化学除草剂的使用，减轻对环境的污染[1–3]。除草机器人多为轮式或履带式，四足机器人因其承载能力强、稳定性好、结构简单[4–5]而优于双足和六足机器人。四足机器人具有良好的抗干扰能力和较高的运动稳定性[6–7]，是保障其快速有效除草的关键，必须选择合理的参数来评价稳定性[8–9]。目前对四足仿生机器人运动稳定性的评判方法有重心投影法、零力矩点法、压力中心法、力–角稳定性度量法等，这些方法主要是针对单一的判据进行分析，使得评判的可靠性不高[10]，而在不规则环境中受到多因素影响的综合评价指标尚未见报道。笔者通过几何分析和公式推导，得出除草用四足机器人在不规则农田环境下行走时判定标准的计算方法，运用数值模拟研究地面倾角、外载荷及外力矩对机器人稳定性的影响，并进行了试验验证。

1 稳定性判定方法

对已有的稳定性判定方法进行综合分析，结合文献[12]和[13]的力–角稳定性度量法及稳定锥法，考虑模块化研究，各模块运用合适的判据进行权重分析，在此基础上提出了三棱锥法。在进行三棱锥法的推导时，作如下假设[11]。

1) 除草用四足机器人足底与地面为点接触，即在地面与足底之间仅有作用力，而没有作用力矩的传递。

2) 稳定性分析仅考虑机器人的倾翻平衡性，忽略足底与地面的相对滑动，即假设足底与地面间的摩擦力无穷大。

图1 为占空比与周期对应曲线，占空比是机器人某条腿处于支撑状态的时间与周期的比值。一个周期内，除草用四足机器人在行走、作业时，一般处于静态步行状态，其占空比ρ，大小为3/4≤ρ＜1，也就是在任何时刻除草机器人在步行过程中最少有三足支撑机体，构成支撑凸多边形。

图1 不同占空比下的周期 Fig.1 Cycle time of different duty factor

对三棱锥法进行定义，如图2 所示。除草机器人的重心为棱锥的顶点O，n 为过重心O 的向量，由除草机器人的四足与地面的接触点作为棱锥的地面角点，以俯视时顺时针方向进行标记，记为Pj(j=1，2，3)，由角点连接而成的凸多边形作为三棱锥的底面，β 是除草机器人沿轴线倾翻的稳定角，θ 为机器人沿角点倾翻的稳定角。

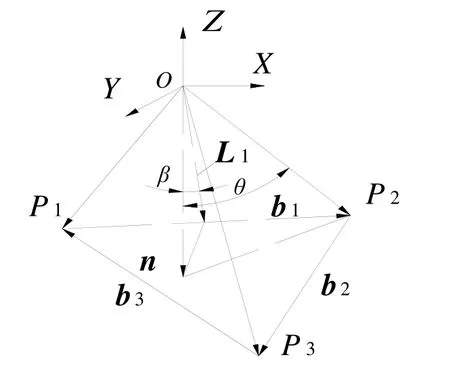
图2 稳定三棱锥示意图 Fig.2 Triangular pyramid method definition

棱锥顶点O 到角点的向量按照角点记为 Pj，则

式中：Pjx为该点在X 轴上的坐标值，Pjy、Pjz同义。

两角点间的直线亦即稳定棱锥的底边定义为倾翻轴线，其向量记为：

过机器人重心O 作与倾翻轴线的法线向量为：

式中：ejb为bj的法向量，

2 稳定性参数的计算

2.1 静态稳定性分析

当除草机器人沿轴线倾翻时，轴线倾翻稳定角β 即为倾翻轴线的法线 jL 和机器人重心向量n 的夹角，可由(4)式得出。

当机器人沿角点倾翻时，角点倾翻稳定角可由式(5)得出。

由上述可知，有轴线倾翻稳定角和角点倾翻稳定角，从机器人整体稳定性来看，取角点倾翻角和与其相邻的2个轴线倾翻角，即：

若要使除草机器人保持稳定，必须选取上述角度中的最小值，亦即最小稳定角γ。

从式(8)可知，γ 越大，机器人越稳定。一般来说，临界倾翻发生在γ=0 时，当γ<0 时，除草机器人会发生倾翻，所以，由上述推导可以发现，要使除草机器人保持稳定，在静力学上需找到一个较大的稳定角γ。

2.2 动力稳定性分析

除草机器人在不规则环境中进行除草作业行走时，易受到外载荷的影响。如果F 和M 分别为外部作用于机器人重心的合力及合力矩，m 为机器人的质量，则机器人受到外载荷时与重力共同作用于重心的合力为F+mg， 故沿倾翻轴线的合外力可用(9)式表达。

由于有M 的存在，故导致倾翻的作用力可等效为式(10)。

稳定角γ 则可由式(4) ～式(8)和式(10)计算得到。

在对机器人进行动力学稳定性分析时，还需考虑除草机器人倾翻时的能量问题[14]，应该考虑在动态情况下机器人绕倾翻轴线或者倾翻角点倾翻所消耗的最小能量。

式中： h 为棱锥重心到底面的距离。

对式(11)中E、h 和g 分别用dim(E)=FL=ML2T–2，dim(h)=L 和dim(g)= LT–2进行无量纲化处理，则式(11)变为

2.3 倾翻性能系数

为了使除草机器人有最大的稳定性，引入倾翻性能系数η 作为机器人倾翻稳定性综合评价指标。

式中：jγ 为稳定计算角，由式(8)定义；φ为除草用四足机器人绕轴线倾翻时的权重影响系数，其取值由动、静力因素和倾翻轴线与运动方向的关系决定。当倾翻轴线与除草机器人运动方向重合或夹角很小时，说明机器人遇到障碍或者地形发生变化等，该系数应适当增加。ψ 为除草用四足机器人绕棱锥角点倾翻的权重影响系数，在不规则地面或受到外力并且有棱锥角点离机器人重心较近时，可能会发生倾翻现象，该系数可适当增加。φ 为除草用四足机器人发生倾翻时能量的权重影响系数，该系数需要考虑机器人在不规则地面的运动方向、惯性力、外载荷等，其值视情况而定。

3 稳定性数值模拟及分析

3.1 初始参数

为了更直观地对稳定性进行分析，根据除草机器人的实际设计尺寸，在MATLAB 中进行了计算并仿真。假定机器人质量分布均匀，在静态情况下由图2 所示坐标系采集到稳定棱锥角点坐标，参照文献[15]所选择的权重系数取值如表1 所示。其他初始化条件如下：机器人质量(m)2 kg，外载荷合力(F) 0～30 N，合外力矩(M)为0～15 N·m，地面倾斜角度0°～45°，倾角方向与机器人运动方向相同。仿真时间为30 s，速度为5 cm/s，采样数据16个，根据(1)～(13)进行计算，根据式(8)和(13)考虑除草机器人的最小稳定角和倾翻性能系数。

表1 稳定棱锥参数 Table 1 Stability pyramid parameters

3.2 最小稳定角分析

图3 为最小稳定角的计算值与拟合值。从图3可以看出,最小稳定角随时间增加呈减小趋势，计算得到最小稳定角最小值为10°，表示此时除草机器人在稳定角为10°的时候发生倾翻，稳定性差；最小稳定角最大值为35°，表示在机器人稳定角最大为35°时发生倾翻，稳定性较好。从计算值分布来看，存在离散现象，说明三棱锥角点坐标规律性不好。影响机器人落足点的因素很多，部分两点之间误差较大是因为此时除草用机器人落足点地面情况变化大，导致两点的坐标变化较大。

对图3 中最小稳定角的变化进行回归分析，运用最小二乘法对所得数据进行三次曲线拟合，最小稳定角γ 近似呈回归式抛物线规律，拟合值与计算值相关程度高，相关系数为0.979 6，这表明所给出的数值计算方法可行。

图3 最小稳定角计算值与拟合值 Fig.3 The computed and fittedminimum stability angle

3.3 倾翻性能系数分析

图4 –a 给出了在合外力矩一定时，合外力和地面倾角对倾翻性能系数的影响曲面，倾翻性能系数波动较大，说明随合外力的增加和地面倾角的变大，倾翻性能系数变化显著，且呈先减小后明显增加趋势。在合外力为11～13 N，地面倾角约为0°时，倾翻性能系数最小，为2.03，表明此时机器人发生倾翻的可能性小，稳定性高。在合外力为21 N，地面倾角为45°时，倾翻性能系数达到最大，为7.32，表明此时机器人发生倾翻的可能性很大，稳定性差。

图4–b 给出了在合外力一定时，合外力矩和地面倾角对倾翻性能系数的影响曲面，倾翻性能系数较平稳，说明随合外力矩和地面倾角的增加，倾翻性能系数变化不显著，呈平缓增大趋势。在合外力矩为15 N·m，地面倾角为45°时，倾翻性能系数最大为4.01。

与合外力矩及地面倾角相比，合外力及地面倾角对机器人稳定性的影响更大，地面倾角对机器人稳定性的影响接近线性单调。

图4 倾翻性能系数响应曲面 Fig.4 Response surface of influence of tip-over coefficient

4 试验验证

为进一步验证除草机器人稳定性评价方法的可行性，试验验证除草机器人的稳定状态，主要考虑其最小稳定角度。根据其结构模型制作的小型四足机器人，其足底有圆形弹性体，与地面近似于点接触，并且弹性体粗糙，与地面摩擦力大，满足三棱锥法所作假设，主要参数：长170 mm，宽130 mm，高140 mm，总质量2 kg(含电池)。结构采用内膝肘式，单腿设置髋关节、膝关节2个自由度，由上位机通过USB 线连接舵机控制板后，在上位机中编写动作组对8个舵机实施控制。

试验在温室玉米地进行。用薄底板依次倾斜叠加0°～45°，对在30 s 内除草机器人行走发生倾翻的角度进行测量。将所测角度值与预测所得的最小稳定角度值对比，结果如图5 所示。试验值与预测值的数据点分布近似，大部分数值相近。经过计算，两者平均相对误差为9.46%。从开始到第2 秒时，2个值都增大，两者之间误差略微减小；从第2 秒到第30 秒结束，2 值均呈现先减小、后增加、再减小的趋势，两者之间误差在第2 秒到第20 秒都增大，在20 s 到28 s 误差减小，28 s 到30 s 误差增大。

图5 最小稳定角仿真值与试验值 Fig.5 Fitted and experiment values ofminimum stability angle

5 结论

在提出三棱锥法的基础上，对除草用四足机器人在不规则农田地面上运动受到惯性力和外载荷等因素影响的稳定性判定标准及综合指标进行了推导。

通过数值模拟计算的最小稳定角与试验值相比，平均相对误差为9.46%，与最小二乘法拟合所得曲线相关程度高，说明了方法具有可行性。

合外力及地面倾角对机器人稳定性的影响显著，倾翻性能系数变化明显。合外力矩及地面倾角对机器人稳定性影响不显著，倾翻性能系数变化平缓。地面倾角对倾翻性能系数的影响近似成线性关系。

[1] 赵匀，武传宇，胡旭东，等．农业机器人的研究进展及存在的问题[J]．农业工程学报，2003，19(1)：20–24．

[2] 孙曼丽．高效智能除草机器人的结构设计与仿真[D]．南京：南京林业大学，2010．

[3] 黄小龙，刘卫东，张春龙，等．苗间锄草机器人锄草刀优化设计[J]．农业机械学报，2012，43(6)：42–46．

[4] 张文宇．四足机器人斜面全方位静态步行及稳定性分析[D]．青岛：中国海洋大学，2009．

[5] 曾翔宇，鄂明成，李冬冬，等．沟壑类非连续地形下的四足机器人运动控制[J]．机器人，2011，33(6)：700–705．

[6] Wei Junming，Shi Zhiguo，Zhang Qiao．Gait and stability analysis of a quadruped robot[C]//Advanced Research on Computer Science and Information Engineering. Zheng zhou：CSIE，2011：347–354．

[7] Shibendu Shekhar Roy，Dilip Kumar Pratihar．Dynamic modeling，stability and energy consumption analysis of a realistic six-legged walking robot[J]．Robotics and Computer-Integrated Manufacturing，2013，29：400–416．

[8] 刘平义，李海涛，张绍英．全地形仿形行走车仿形行走理论及试验[J]．农业工程学报，2012，28(增刊2)：134–139．

[9] Zhang Lei，Gao Shan．Normalized energy stability margin based analysis of omni-directional static walking of a quadruped robot on rough terrain[C]//International Conference on Manufacturing Science and Technology. Piscataway：IEEE，2012：7401–7405．

[10] David C Remy，Keith Buffinton，Roland Siegwart. Stability analysis of passive dynamic walking of quadrupeds[J]．International Journal of Robotics Research，2010(29)：1173–1185．

[11] 王鹏飞，黄博，孙立宁．四足仿生机器人稳定性判定方法[J]．哈尔滨工业大学学报，2008(7)：1063–1066．

[12] Karl Iagnemm，Adam Rzepniewskia．Mobile robot kinematic reconfigurability for rough-terrain[C]// Proceed- ings of the SPIE：Sensor Fusion and Decentralized Control in Robotic Systems III．Boston：Massachusetts，2000：5–8．

[13] Papadopoulos E G，Rey D A．A new measure of tip-over stability margin for mobile manipulators[C]//Proceedings of the IEEE Int Conf on Robotics and Automation. Minneapolis：IEEE，1996：3111–3116．

[14] 李斌，刘金国，谈大龙．可重构模块机器人的倾翻稳定性研究[J]．机器人，2005，27(3)：241–246．