类铍离子1s2 2snp 3P(n=2 ～6，Z=5 ～8)态能级和精细结构参数的理论计算

谢国秋

(黄山学院信息工程学院，黄山245041)

1 引 言

原子结构是原子物理学中一个重要的研究内容，而精确的原子精细结构数据更是原子物理学家所需要的，它对理解原子内部结构、原子定标等方面的应用都具有重要的意义. 类铍离子的原子核外有四个电子，其包含了电子与电子之间的各种相互作用. 因此，人们常把铍原子作为多电子原子理论模型的验证平台，并对其展开了一系列的研究工作［1-12］. 其中包括对波函数的改造，如全实加关联波函数［1，2］和组态相互作用波函数［3-7］，并取得了很好计算结果，但是，波函数的构造比较复杂;此外，还包括对哈密顿的改造，如黄时中等［8，9］，依据最弱受约束电子势模型理论，计算了铍原子单激发态和双激发态里德堡系列能级和量子亏损取得了很高的计算精度，但是这种理论需要实验数据作为启动值，也无法得到各能级的波函数.

2009 年，刘芬等［10］利用对角和法则，导出了铍原子和类铍离子1s22snp 组态非相对论能量的解析表达式，在考虑电子间交互作用以及内外壳层电子的不同屏蔽效应的基础上，利用变分原理具体计算了类铍离子1s22snp(n=2 -6，Z=4 -8)组态的非相对论能量值;2012 年，谢国秋等［11］以Breit-Pauli 哈密顿的球张量形式为基础，借助不可约张量理论，对类铍原子1s22snp 组态能量的相对论修正(包括质量修正项、单体达尔文修正项、双体达尔文修正项和自旋-自旋接触相互作用修正项)进行了具体计算;2013 年，马堃等［12］借助不可约张量和角动量耦合理论，导出了铍原子1s22snp 组态精细结构的解析表达式，并进行了具体计算，计算结果与已有的数据进行了比较，具有很好的一致性. 本文在文献［12］的基础上，将该理论进一步拓展到类铍离子，具体地，解析地导出类铍离子1s22snp(n=2 -6)3P 态精细结构(包括自旋-轨道相互作用、自旋-其它轨道相互作用和自旋-自旋相互作用)的解析表达式，并利用我们所开发的计算程序，各项进行具体地计算，计算结果与文献符合地较好. 同时，我们还计算了1s22snp (n =2 -6)3P 态精细结构参数A 和B 的值.

2 理论基础

准相对论框架下的多电子原子精细结构的计算，在文献［13，14］中已经有较为详细的论述，本文不再累述，这里仅简单地介绍一下计算的理论框架. 多电子原子的精细结构哈密顿采用如下的表达形式

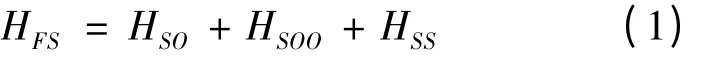
上式右边的三项分别表示自旋-轨道相互作用哈密顿、自旋-其它轨道相互哈密顿和自旋-自旋相互哈密顿，它们的具体形式在文献［13］中给出. 采用耦合的Racah 表象，类铍离子的精细结构能量为［13］

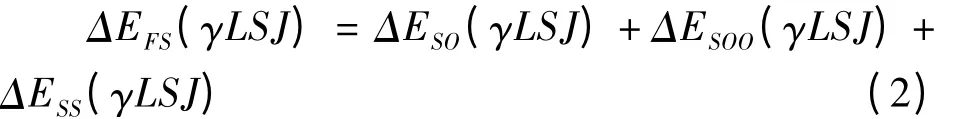
其中

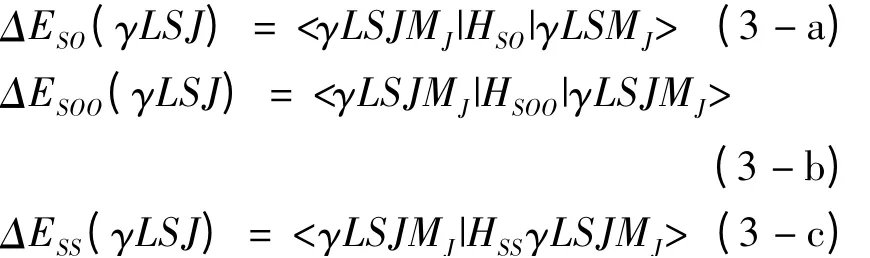
(3)式中的|γLSJMJ＞是LS 耦合Racah 波函数，它可以根据角动量耦合理论表示为非耦合Racah 波函数的线性组合，即

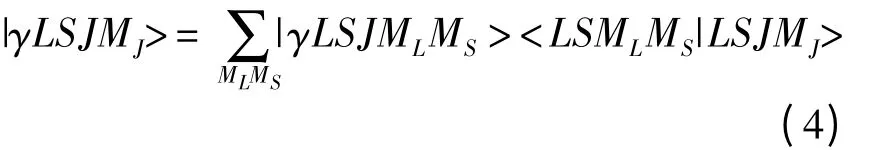
这里，|γLSMLS＞|γLSJMLMS＞是多电子原子的非耦合Racah 波函数，可以进一步表示为Slater 波函数的线性组合，即

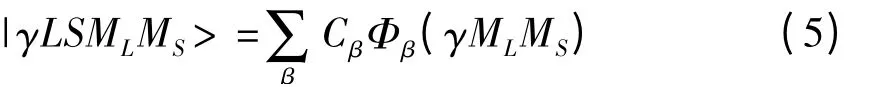
此处，Φβ( γMLMS)即为Slater 波函数，具体形式为

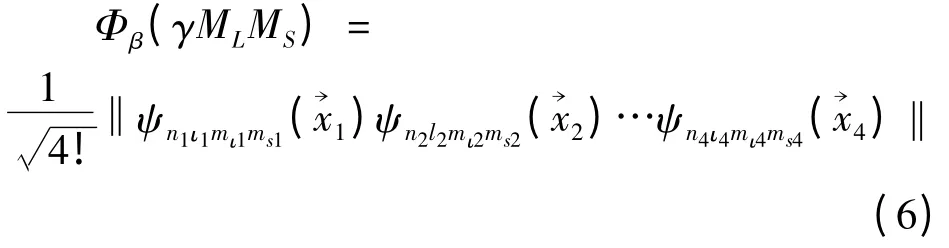
式 中 ‖…‖ 是 4 × 4 行 列 式，ψn1ι1mι1ms1()ψn2ι2mι2ms2)…ψn4ι4mι4ms4()表 示 行列式的主对角项，而ψniιimιimsi(→xi)为单电子波函数，它由单电子径向波函数、角向波函数和自旋波函数直接乘积得到，即

单电子角向波函数和自旋波函数都是已知的，而单电子径向波函数采用Slater 型径向波函数［15］进行构造.

从(3 -5)式中，我们能够看出，计算精细结构能级ΔEFS(γLSJ)的关键问题是计算自旋-轨道相互作用哈密顿、自旋-其它轨道相互作用哈密顿和自旋-自旋相互作用哈密顿在Slater 波函数下的一系列对角矩阵元与非对角矩阵元，即

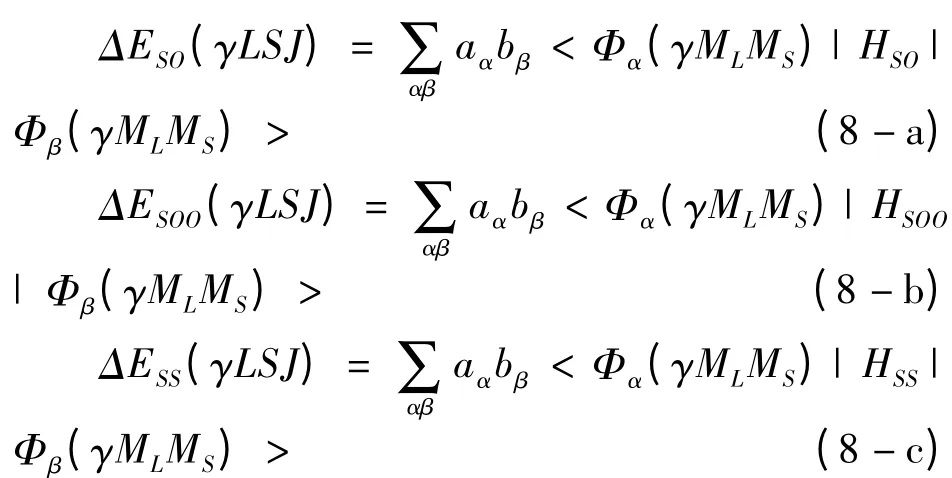
值得注意的是，在文献［12］中，利用不可约张量理论，完成了(3)式对角元的角向积分和自旋求和部分，并给出了只含有径向积分的解析表达式. 利用这些解析表达式，我们可以进一步计算出类铍离子1s22snp(n=2 -6)3P 态精细结构能级和自旋参数A 和B 的值.

3 计 算

3.1 精细结构能级的计算

考虑精细结构劈裂后，类铍离子1s22snp(n=2 -6)3P 态能级分裂为三个，即3P2，3P1和3P0.因为不考虑外场和核自旋效应，因此，磁量子数MJ对能级结构没有影响，为方便计算，我们取MJ= J. 借助(4)式和(5)式，并利用角动量耦合理论，这三个精细结构谱项可以表示为Slater 波函数的线性组合

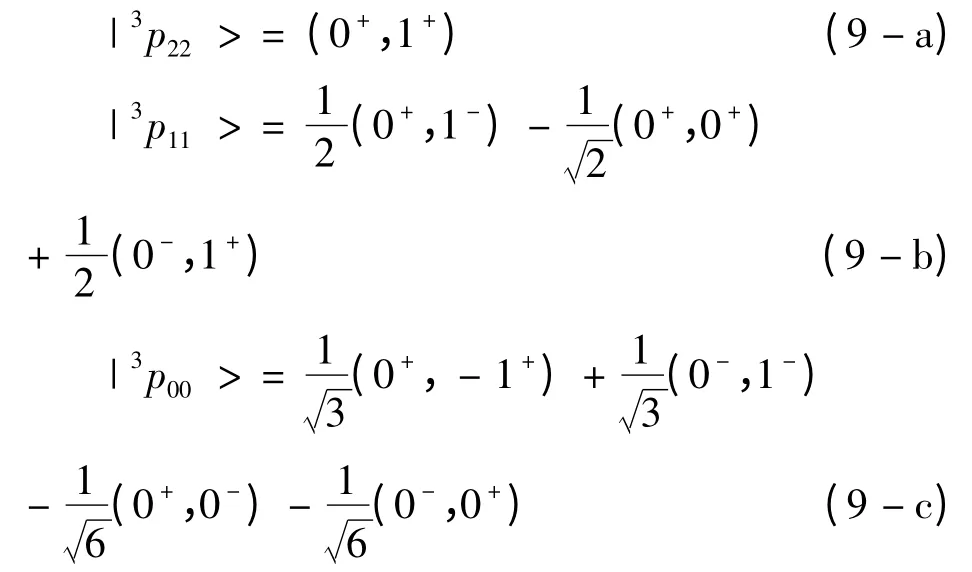
式中，(0+，1+)是Slater 行列式的简记形式，具体形式为

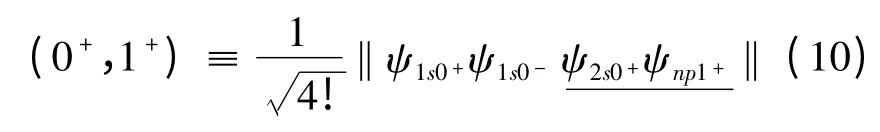
将(9)式代入(3)式，利用不可约张量理论和角动量理论，完成所有的角向积分和自旋求和部分. 最后，再利用本文所采用的径向波函数，进一步完成径向积分部分，从而得到仅仅与径向波函数里面的变分参数有关的精细结构解析表达式.我们将文献［10］中的变分参数代入，即可得到类铍离子1s22snp(n=2 -6)3P 组态具体的精细结构的数值. 为了简化计算，我们开发了一套程序，利用该程序计算了类铍离子1s22snp(n =2 -6)3P组态精细结构(自旋-轨道相互作用能量、自旋-其它轨道相互作用能量和自旋-自旋轨道相互作用能量)的数值，结果列于表1. 在表2 中，给出了类铍离子1s22snp(n =2 -6)3P 组态的能级，并将计算的能级与NIST［16］的值进行了比较，其中，包含非相对论能量、相对论修正能量和精细结构.

表1 类铍离子1s22snp(n=2 -6)3P 组态的精细结构(单位:cm -1)Table 1 Fine-structure energies of the 1s22snp(n=2 -6)3P state in Be-like ions(Unit:cm -1)

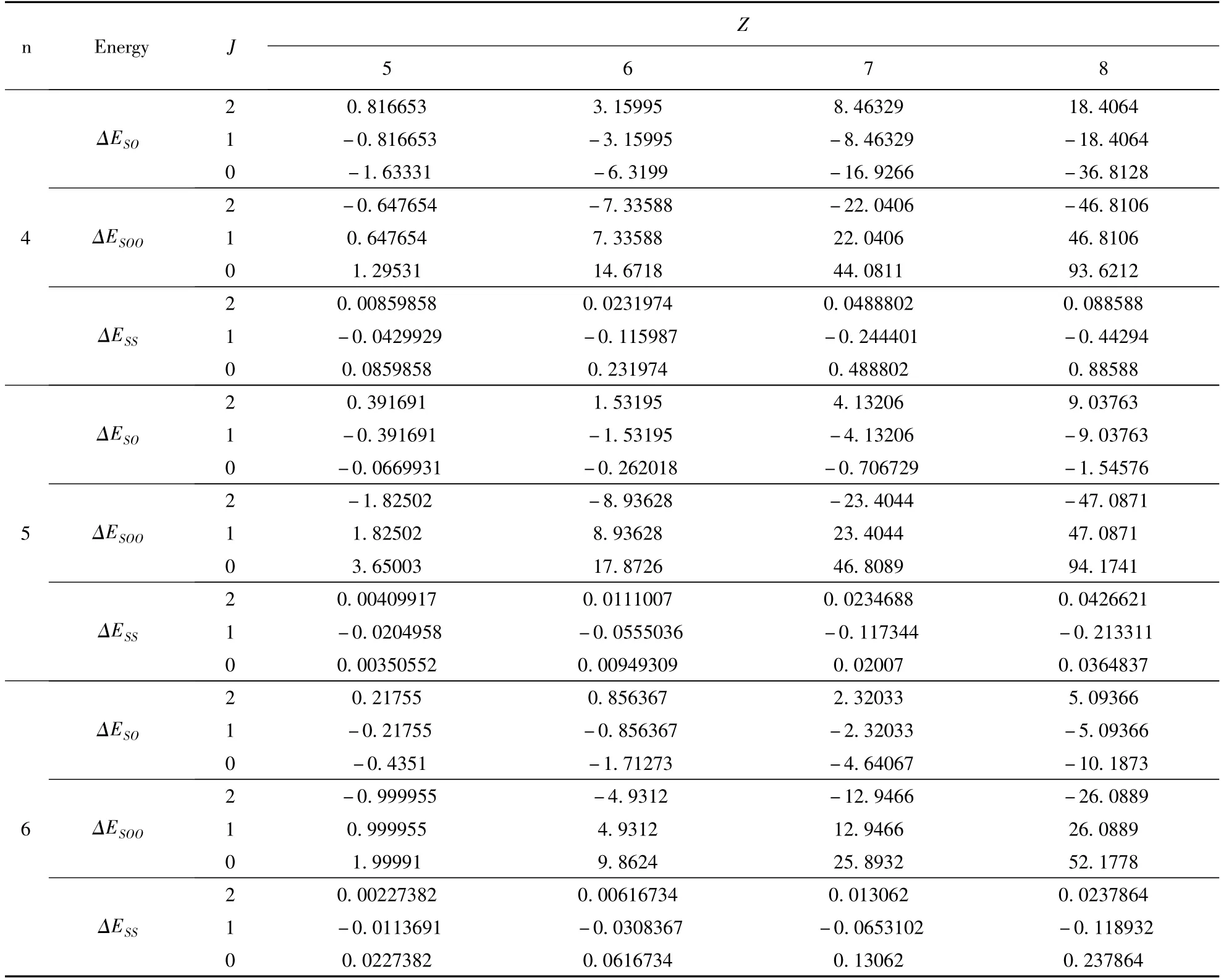
续表1

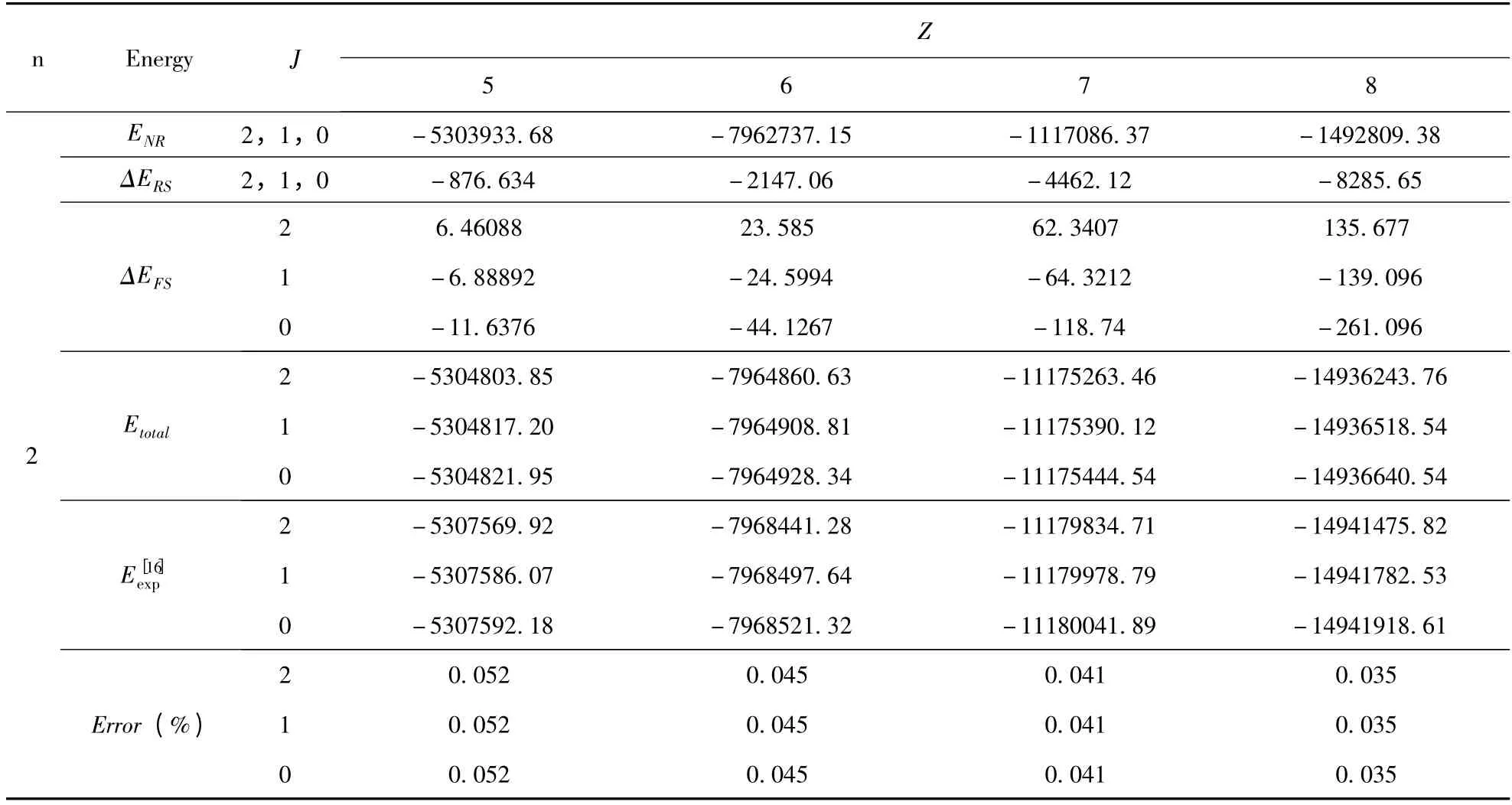
表2 类铍离子1s22snp(n=2 -6)3P 组态的能级(单位:cm -1)Table 2 The energies of the 1s22snp(n=2 -6)3P state in Be-like ions(Unit:cm -1)

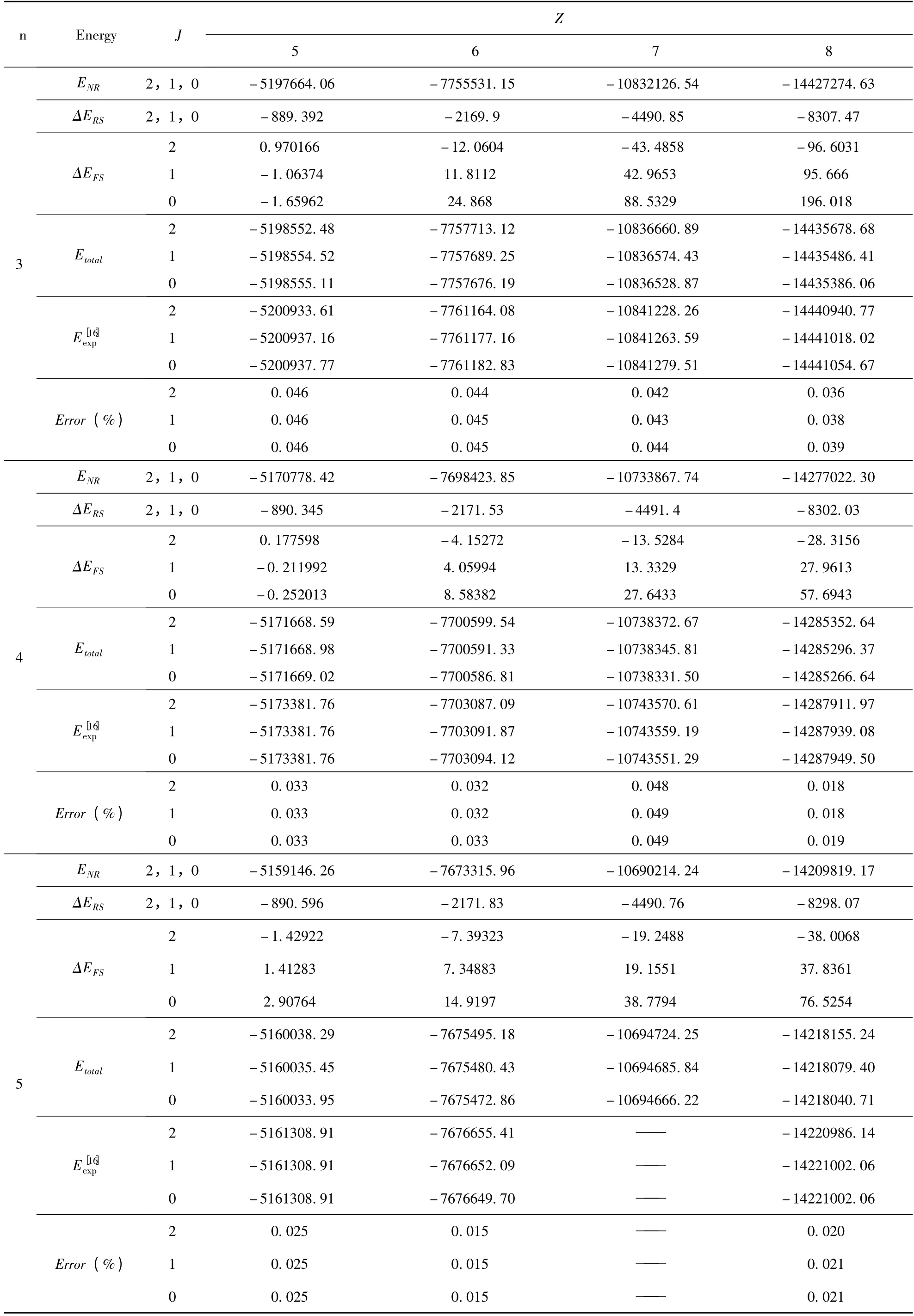
续表2

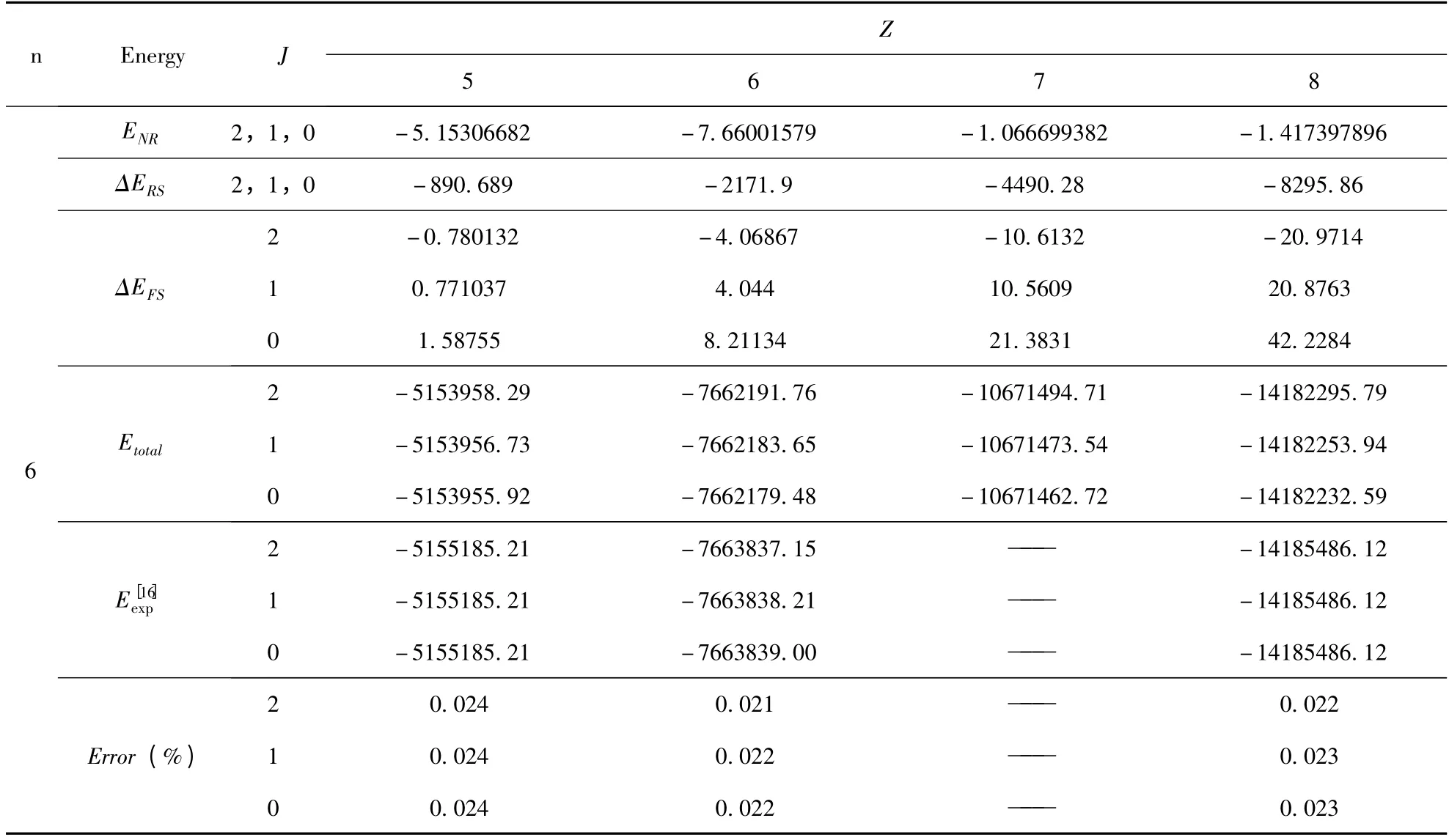
续表2

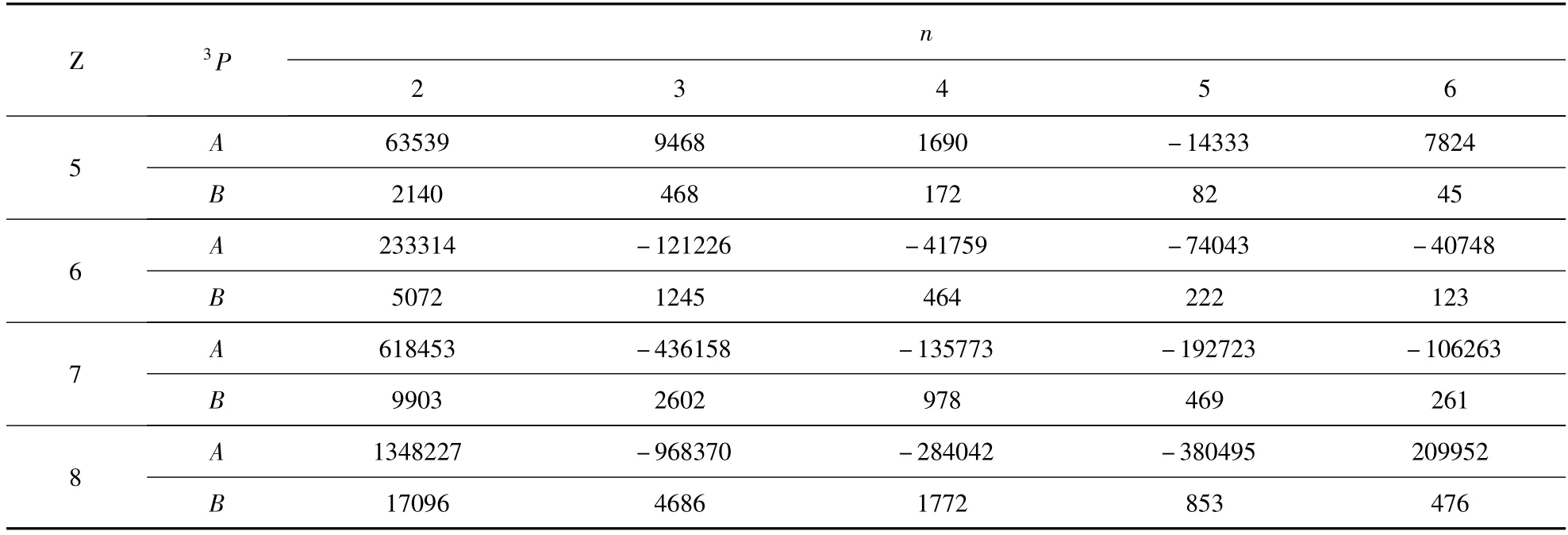
表3 类铍离子1s22snp(n=2 -6)3P 组态的精细结构参数(10-4cm-1 )Table 3 Fine-structure parameters of the 1s22snp(n=2 -6)3P state in Be-like ions(10-4cm-1 )

3.2 精细结构参数的计算

仔细分析表1，我们可以看出，精细结构分裂三个分支所对应的能量值具有很强的规律性，而自旋-轨道相互作用项与自旋-其他轨道相互作用项的能量值所体现的规律性完全相同，如，B+1s22s2p3P 态，J=0 的自旋-轨道相互作用能量是J=1 的2 倍，是J=2 的-2 倍等，这些规律主要是源自自旋-轨道相互作用和自旋-自旋相互作用可以写成精细结构哈密顿的有效形式［14］，即

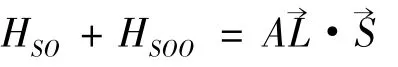
式中A 是总自旋-轨道相互作用参数，它由自旋-轨道相互作用和自旋-其它轨道相互作用两部分贡献，且与L 和S 量子数有关，即A = A(LS);B 是自旋-自旋相互作用参数，其值也与L 和S量子数有关，即B = B(LS). A、B 参数对于从事光谱实验工作者具有重要的作用. 本文在表1的基础上，进一步计算了铍原子1s22snp(n =2 -6)3P 组态的精细结构参数A 和B 的数值，其结果列于表3.

4 讨 论

本文基于多电子原子精细结构哈密顿的球张量形式，并借助不可约张量理论和角动量耦合理论，计算了类铍离子1s22snp(n=2 -6)3P 组态精细结构的能级，结果与实验值符合的较好. 另外，需要说明的是，在本文中，我们采用Slater 型径向波函数的领头项，它类似于类氢原子的径向波函数，即

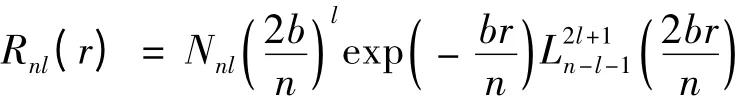
［1］ Chung K T，Zhu X W. Energies，fine structures and isotope shift of 1s22snl excited states of the beryllium atom［J］. Phys. Rev.，1993，48:1944.

［2］ Chung K T，Zhu X W. Energies and fine structures of 1s22snp (n=2，3)1Poand3Po2，1，0states of Be-like ions［J］. Phys. Rev.，1994，50:3818.

［3］ Fischer C F. Allowed transit ions and intercombinat ion lines in CⅡand CⅢ［J］. Phys. Scr.，1994，49:323.

［4］ Tachiev G，Fischer C F. Breit -Pauli energy levels，lifetimes，and transition data:beryllium -like spectra［J］. J. Phys. B:At. Mol. Opt. Phys.，1999，32:5805.

［5］ Kingston A E，Hibbert A. Breit-Pauli calculations of the energy levels and oscillator strengths of Be-like ions［J］. J. Phys. B:At. Mol. Opt. Phys.，2000，33:693.

［6］ Han L H，Zhang R. The energy calculation of the excited state for berylliuml ike ions［J］. J. At. Mol.Phys.，21(3):441(in Chinese)［韩利红，张茹. 类铍离子激发态的能量计算［J］. 原子与分子物理学报，2004，21(3):441］

［7］ Han L H，Lu P F. Relativistic energies and transition rates of the excited states for Be - like CIII and OV［J］. J.At. Mol. Phys.，2005，22(4):681(in Chinese)［韩利红，芦鹏飞. 类铍CⅢ和OⅤ离子激发态的相对论能量和跃迁几率［J］. 原子与分子物理学报，2005，22(4):681］

［8］ Huang S Z，Ma K，Yu J M，et al. Energies of doubly excited states 1s22pnd1Po1(n =3 -50)of beryllium atom［J］. J. At. Mol. Phys. (原子与分子物理学报)，2008，25(5):1211(in Chinese)

［9］ Huang S Z，Liu F，Ma K，et al. Calculation of rydberg energy levels for beryllium atom［J］. J.At. Mol.Phys.(原子与分子物理学报)，2010，27(4):637(in Chinese)

［10］ Liu F，Huang S Z. Energy of the 1s22snp state of beryllium-like atoms［J］. J. Anhui Nor. Uni. (Natural Science Edition)，2009，32:541 (in Chinese)［刘芬，黄时中. 类铍原子1s22snp 组态的非相对论能量［J］.安徽师范大学学报(自然科学版)，2009，32:541］

［11］ Xie G Q，Ma K，Jiao Z. Relativistic corrections to ls22sn p state energies in the Beryllium - like atoms［J］. J. Sichuan Uni. (Natural Science Edition)，2012，49(2):409(in Chinese)［谢国秋，马堃，焦铮. 类铍离子1s22snp 组态能量的相对论修正［J］.四川大学学报(自然科学版)，2012，49(2):409］

［12］ Ma K，Chu Y，Jiao Z，et al. Theoretical calculation of fine-structure for 1s22snp3P state in beryllium atom［J］. J.At. Mol. Phys.，2013，30(4):549(in Chinese)［马堃，褚园，焦铮，等. 铍原子1s22snp3P态精细结构的理论计算［J］.原子与分子物理学报，2013，30(4):549］

［13］ Huang S Z，Ma K，Ni X B，et al. Fine-structure of the ground state of carbon - like atoms［J］. J. At.Mol. Phys.(原子与分子物理学报)，2008，25(2):321(in Chinese)

［14］ Huang S Z. Theory of atomic structure［M］. Hefei:USTC Press，2005，226 -236(in Chinese)［黄时中.原子结构理论［M］. 合肥:中国科学技术大学出版社，2005，226 -236］

［15］ Slater J C. Quantum theory of atomic structure［M］.Vol. 1. New York:McGraw-Hill，1960.

［16］ NIST Atomic Spectra Database. Energy Levels Data［DB］.National Institute of Standards and Technology.Available:http://physics.nist.gov/asd.