高频强激光场中H- 电离特性理论研究

高婉琴，王加祥，魏 启

(华东师范大学精密光谱科学与技术国家重点实验室，上海200062)

1 引 言

在许多生化过程的催化反应中，由As，S，P，Se 等元素构成的高价负离子起着极其重要的作用，比如，，，等等.通过对这些负离子的研究，人们进一步发现，自然界中的高价负离子一般总是存在于溶液和固体中，象硫酸铜溶液中，而在气相则只能以带负电荷的分子形式存在，比如在离地球表面20 到120 公里的大气层可以发现如下处于气相的负离子:，OH-，，. 为了探究处于气相的单原子最多能束缚几个电子，早在上世纪60、70 年代，人们就开展了大量的相关实验工作.Stuckey、Kiser、Baumann 等人都曾宣称发现如下的高价负离子:P2-，O2-，F2-，Cl2-，As2-，Sb2-，Te2-，Bi2-，Br2-［2，3］但后来的实验都推翻了这些发现. 到现在为止，所有的实验都表明只有负一价的单原子离子或负二价的分子可能在气相存在［4-6］. 这些结论也得到大量的理论分析和数值计算的验证［7-10］.

近年来随着强场物理的快速发展，人们发现，如果提高激光场强度或增加激光频率，处于光场中的原子可能变得更加稳定. 这种稳定性可以分为两种，一种是动力学稳定性，即在激光场强度达到一定阈值时，原子的电离率会逐步下降［11］.另一种是绝热稳定性，即在高频强场下，利用Krammers-Henneberger (KH)变换，可以把原子看成一个稳态而不再电离［12］. 后一种稳定性很容易让人想到是不是可以让这种更加稳定的原子束缚更多的电子，从而形成高价态负离子. 近年来，人们开始把目光瞄准了高频强场中高价负离子的稳定性问题. van Duijn 等人首先利用HFFT 理论(high frequency Floqeut theory)证明了负二价的氢离子在线偏振及圆偏振激光场下的稳定性［13］. 之后Kais 小组用类似的方法证明了Li2-，He-，He2-等在强场下也具有稳定的束缚态［14，15］.

尽管在理论上，高频强场中高价负离子的发现和研究已经有十几年了，但是至今为止这种现象还没在实验中被直接发现，因为它所需要的稳态高频强激光场在实验上实现有较高难度.

那么，如何从实验上验证此类高价负离子态在强激光场中稳定存在成为大家非常关心的一个重要课题. 本文将以稳态H-为例，利用它在外加激光场下电离后光电子的特性来为将来的实验探索提供理论依据. 在我们的工作中，将采用研究电离经常使用的相空间平均法来探讨H-的光电离情况，重点探究外加激光场强度、激光的频率对于电离情况的影响.

2 模型和方法

图1 展示了高频强场中负一价氢离子H-与外加强激光场相互作用的示意图. 高频场的偏振方向为z 方向. 为了研究该H-的电离情况，我们沿z 轴方向入射一束线极化的强激光.

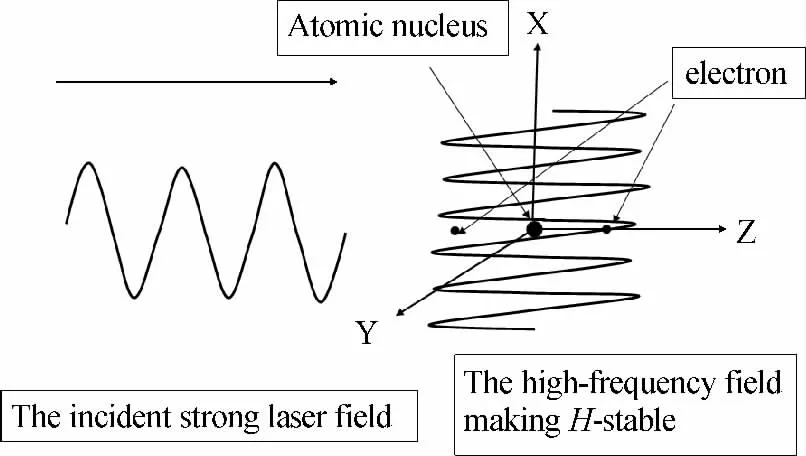
图1 稳定于高频强场中的H -与外加强激光场相互作用示意图Fig.1 Schematic diagram of the interaction between H -in the KH frame and the incident strong laser field

本文采用原子单位，高频场的场强固定为α0=200a. u. . 数值研究表明，在此高频场作用下，负一价氢离子可以稳定存在，相应的基态波函数可以通过Hartree-Fock (HF)方法获得，详细的计算见文献［14］，这里只给出相关的结果，作为我们电离计算的出发点. 图2 给出了H-波函数所对应的电子概率分布图，其中两个电子中心距离约为400a. u. . 从图中可以看出两个电子分别束缚在有效势阱的两个最低点，它们的间距正比于高频场的激光场强，远大于单电子波函数的空间尺寸，因此电子间初始关联很弱，单电子的基态束缚能为E= -1.6354 ×10-2a. u.［14］.

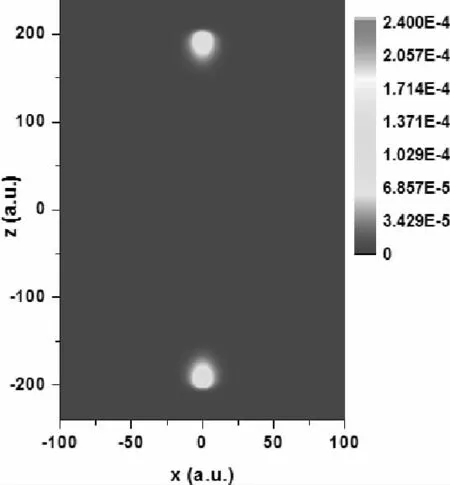
图2 高频强场中H -对应的电子概率分布图. 电场强度为α0 =200a.u.Fig.2 Probability distribution of the electrons from H -in the high - frequency laser fields with intensity α0 =200a.u.

有了H-的基态波函数后，我们将利用相空间平均法来计算其电离特性. 相空间平均法是由Leopold等人引入用来描述高激发态原子、分子在低频激光或者微波辐射场中动力学的一种数值计算方法［16］.其核心是在经典相空间利用统计抽样的方法来获得所对应量子态要求的粒子概率密度分布.

3 结果分析

本文采用的外加激光为高斯包络脉冲，其表达形式为，

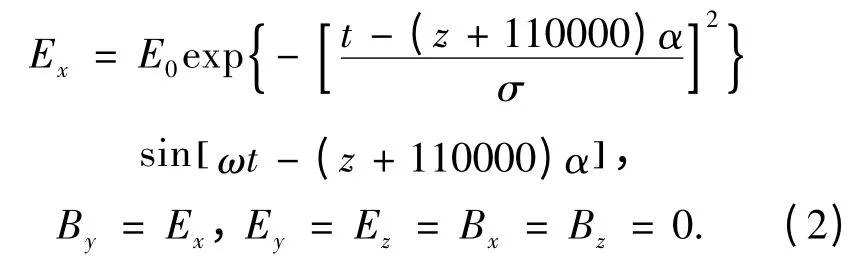
其中Ex，Ey，Ez，Bx，By，Bz分别是外加激光场在x，y，z 方向上电场和磁场分量，E0是入射激光脉冲的场振幅，σ 用以表征脉冲长度.

3.1 电离率

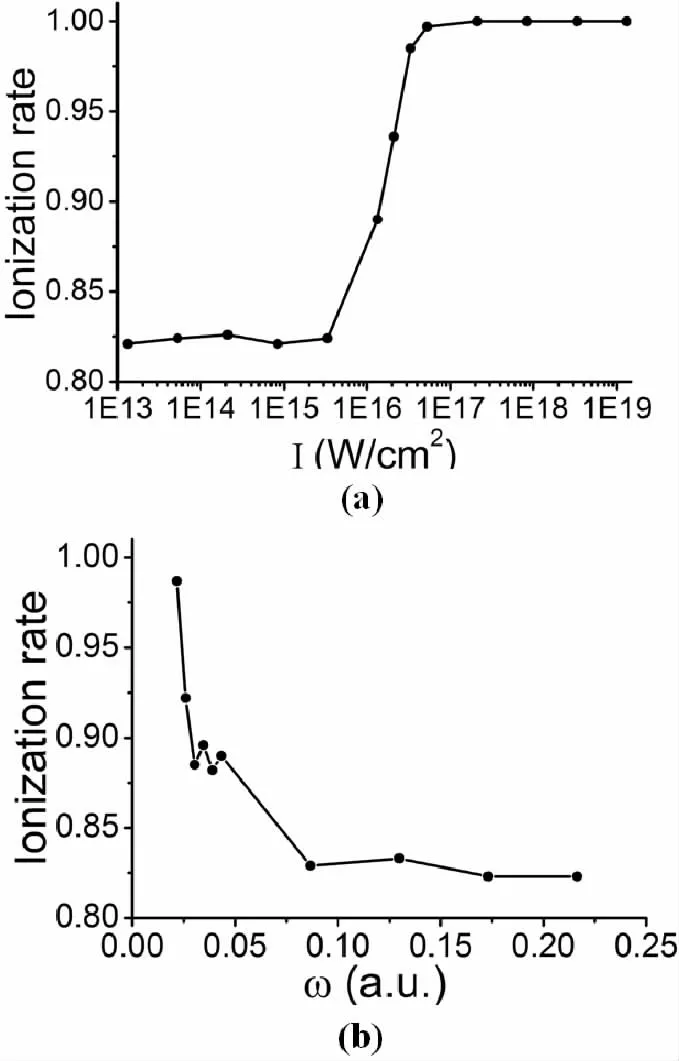
图3 稳定于高频场中的H - 电离率随外加激光场强度［(a)］和频率［(b)］的变化. (a)ω =0.0433a.u.，τ=8fs. (b)I=1016W/cm2，τ=8fsFig.3 Dependence of the ionization rate of H -in the highfrequency laser fields upon the intensity. (a)(where ω = 0.0433a.u.，τ = 8fs)and frequency.(b)(where I=1016 W/cm2，τ =8fs)of the incident intense laser field

图3 (a)给出了H-在外加激光场作用下至少有一个电子电离的电离率随激光场强度的变化.从图中可以看出电离率随着激光场强度的增加而增加，在I=1016W/cm2左右增幅较为明显，直到完全电离，这是由于H-的束缚能较低，比较容易失去一个电子. 图3 (b)为电离率随激光频率的变化，可以看出当频率小于0.0433 时，随着频率的增加，H-的电离率有小幅度的降低. 当频率大于0.0433，频率的变化对电离率的影响很小，这表明电离率对激光场频率的增加有饱和效应. 原因在于，当激光频率较高时，电子还没来得及远离势阱中心时，就会被反向的电场拉回来，因此更加不容易电离. 考虑到H-的电子基态能量为E= -0.01635，一般而言，当外加激光场的频率增加到和电子的束缚能一个数量级时，电离率对频率的依赖开始变小.

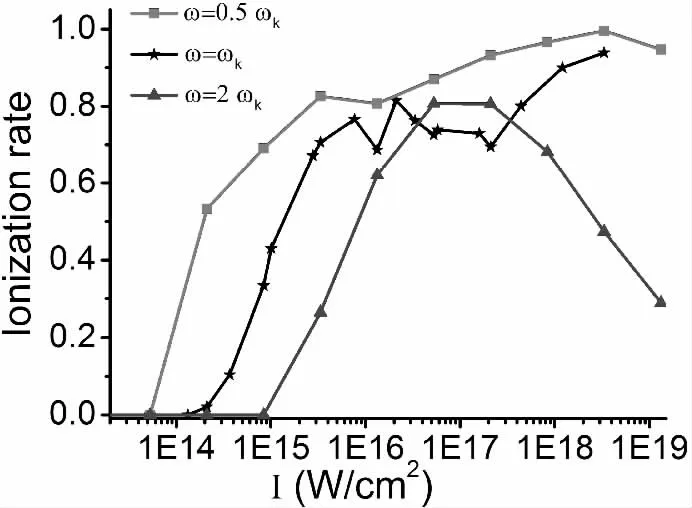
图4 在不同激光频率下氢原子的电离率随激光场强度的变化Fig.4 Dependence of the ionization rate of hydrogen atom upon the laser field for different laser frequencies

作为对比研究，我们还计算了氢原子在线性偏振的单色激光脉冲下的电离情况. 由于氢原子中的电子轨道半径远小于激光波长，所以可以应用偶极近似. 取激光场电场分量为E(t)= E0f( )t sin(ωt)，其中f(t)=sin(πt/TD)(0 ≤t ≤TD).这里的脉冲形状因子取为正弦形式，主要是为了便于和已有文献上计算结果的比较［17］. 图4 是氢原子的电离率随激光强度的变化. 这里的计算结果和文献［17］的基本相同，这从一个侧面也验证了我们计算程序和算法的可靠性. 从图中我们可以看到随着激光强度的增强和脉冲频率的降低，氢原子的电离率也是有所增加，不过整体上的电离率比对应的H-的电离率低，这很容易理解，因为H-的束缚能比H 的低很多. 当光强增加到一定的数值之后，氢原子的电离出现了抑制的现象，并且这种抑制现象对激光频率有明显的依赖. 当ω=0.5 时，氢原子的电离率随着激光强度的增加上升到0.85 左右之后并没有明显的抑制现象. 当ω=1 时，在5 ×1016W/cm2＜I ＜3 ×1017W/cm2的情况下，电离率出现了下降的现象，然后随着场强的进一步增强，电离率又再次增加. 当ω =2 时，氢原子的电离抑制现象则极为明显，在I ＞1 ×1017W/cm2情况下，电离率出现了明显的下降的现象.这些计算结果表明，激光频率的增加对氢原子的稳定性增强有很大作用. 而我们从图3 与图4 的对比中可以看出H-的电离并不存在H 电离时的抑制现象.

3.2 光电子角分布

从实验角度看，光电子的角分布更直接反映了H-的电离特征，下面我们着重探究了激光场强度及脉冲频率对光电子角分布的影响. 首先，作为对比，我们把高频场直接卸载. 由于没了高频场对H-的稳定作用，其中的电子将会直接电离掉，相应的电子角分布如图5 所示. 本文中所有的电子将分布图都是以x 轴为的极坐标的极轴. 从图中可以看出，光电子在与x 轴夹角为90°和270°的方向上分布最多，这正是高频场的极化方向.

图5 使H -稳定存在的高频场直接卸载后光电子角分布Fig.5 Angular distribution of the ionized electrons when the high-frequency laser field is switched off abruptly

接下去，我们再来计算外加激光场的强度和频率对H-电离后光电子角分布的影响. 图6 给出是角分布随激光强度的变化情况. 激光频率ω =0.0433，脉冲持续时间约为8fs. 激光场强度则分别取为I=1013W/cm2，I =1016W/cm2，I =1017W/cm2，I=1018W/cm2. 从图中可以看到当I =1013W/cm2时，此时的光电子角分布与H-在高频场直接卸载后电子角分布几乎无差别，而随着激光场强度的增加，这种差别越来越大，当I =1018W/cm2时，光电子的分布基本在同一个方向上. 这主要是由于外加激光场的极化方向沿着x 轴，所以随着激光强度的提高，电离后的电子越来越倾向于沿着x 轴的方向出射.

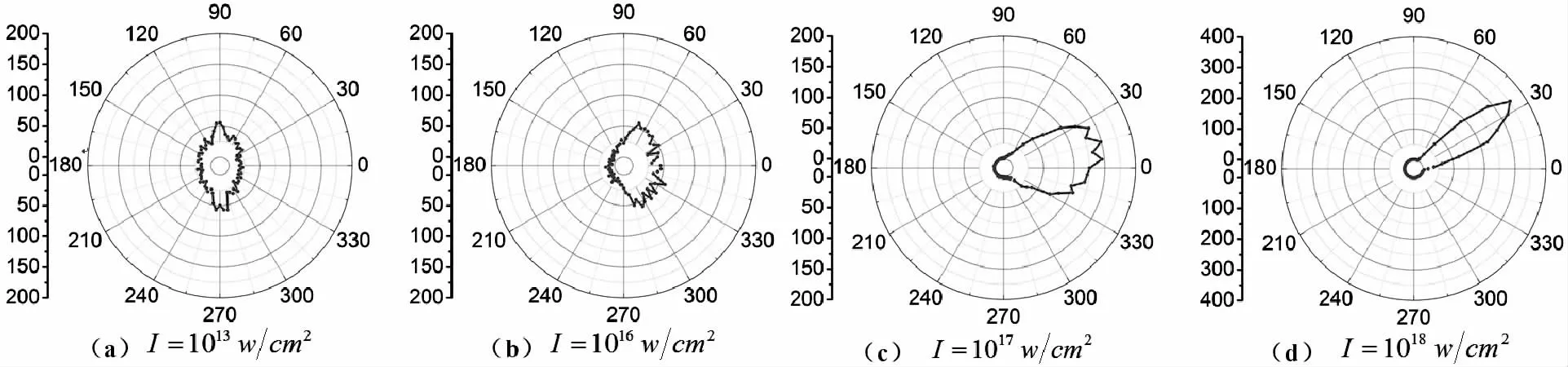
图6 不同激光场强度下H -电离后的光电子角分布Fig.6 Angular distribution of ionized electrons fromH -for different laser field intensities

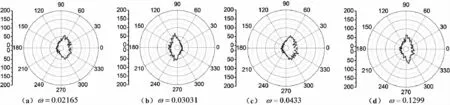
图7 不同激光频率下H -电离后的光电子角分布Fig.7 Angular distribution of the ionized electrons from H - for different laser frequencies

图7 给出了激光频率对光电子角分布的影响.所取激光场强度I =1016W/cm2，脉冲持续时间约为8fs，脉冲频率ω 分别为0.02165、0.03031、0.0433、0.1299. 我们发现当脉冲频率大于0.1299 时，光电子角分布与H-在高频场直接卸载后电子角分布差别不大，光电子在与x 轴夹角为90°和270°的方向上分布最多. 这表明外加高频电场对电子电离的影响很小，这和前面电离率的计算结果保持一致. 而当脉冲频率低于0.1299时，电子角分布则出现左右“摇摆”的情况，这主要反映了在激光波长较长时，激光位相对电子电离的影响.

4 结 论

从本文数值模拟结果的讨论与分析，我们可以得出下面几个结论.

1)H-的电离率比氢原子的电离率高，具有较高的光电子产额.

2)当激光强度增加时，H 会出现电离抑制现象，而H-由于电离能低很多，则没有这种现象.

3)在激光频率较低时，从H-电离后的电子基本沿着激光场的极化方向，即x 方向出射. 然而，随着激光场频率的增加，电子的角分布越来越倾向于沿z 方向出射，并且越来越接近把高频场直接卸载后光电子的角分布.

以上这些H-光电离的特征可以为将来实验验证高频强场条件下高价负离子的存在性提供有效的理论依据. 对于更高价态负离子电离特性的研究将是我们下一步工作的重点.

［1］ Kopp E. The Upper Atmosphere［M］. Berlin:Springer，1996.

［2］ Stuckey W K，Kiser R W. Doubly charged negative ions of oxygen，fluorine，chlorine and bromine ［J］.Nature，1966，211(5052):963.

［3］ Baumann H，Heinicke E，Kaiser H J，et al. On the existence of doubly negative charged heavy ions［J］.Nuc. Instr. Meth.，1971，95(2):389.

［4］ Schauer S N，Williams P，Compton R N. Production of small doubly charged negative carbon cluster ions by sputtering［J］. Phys. Rev. Lett.，1990，65(5):625.

［5］ Scheller M K，Cederbaum L S. Stability of MX2-3ions in the gas phase and when do ionic molecules have large ionization potentials ［J］，J. Chem. Phys.，1993，99(1):441.

［6］ Blades A T，Kebarle P. Study of the stability and hydration of doubly charged ions in the gas phase:，，，and some related species［J］.J. Am. Chem. Soc.，1994，116(23):10761.

［7］ Massey Hs W. Negative ions［M］. 3rd edition，England:Cambridge University Press，1976.

［8］ Sherwood C R，Hanold K A，Garner M C，et al.Translational spectroscopy studies of the photodissociation dynamics of O4-［J］. J. Chem. Phys.，1996，105(24):10803.

［9］ Scheller M K，Compton R N，Cederbaum L S. Gasphase multiply charged anions ［J］. Science，270(5239):1160.

［10］ Kais S，Serra P. Quantum critical phenomena and stability of atomic and molecular ions［J］. Int. Rev.Phys. Chem.，2000，19(1):97.

［11］ Su Q，Eberly J H. Stabilization of a model atom in superintense field ionization ［J］. Opt. Soc. Am. B，1990，7(4):564.

［12］ Gersten J I，Mittleman M H. The shift of atomic states by laser fields［J］. Phys. B，1976，9(15):2561.

［13］ van Duijn E，Gavrila M，Muller H G. Multiply charged negative ions of hydrogen induced by superintense laser fields［J］. Phys. Rev. Lett.，1996，77(18):3759.

［14］ Wei Q，Kais S，Moiseyev N. New stable multiply charged negative atomic ions in linearly polarized superintense laser fields［J］. Chem. Phys.，2006，124(20):201108-1.

［15］ Hoehn R D，Wang J，Kais S. Dimensional scaling treatment with relativistic corrections for stable multiply charged atomic ions in high -frequency super -intense laser fields［J］. Chem. Phys.，2012，136(3):034114-1.

［16］ Leopold J G，Percival I C. Ionisation of highly excited atoms by electric fields III. microwave ionisation and excitation［J］. Phys. B，1979，12(5):709.

［17］ Bauer J，Brewczyk M，Rzazewski K. Classical simulations for atoms and molecules in intense laser fields［J］. Laser Physics，2000，10(1):177.