在同位旋空间中正反质子弹性散射的重整化混合圈链图效应
2015-07-13陈学文张家伟
文 毫,陈学文,张家伟
(1. 重庆大学理论物理研究所,重庆400044;2. 重庆科技学院,重庆401331;3. 南安普敦大学,南安普敦SO17 1BJ,英国)
1 Introduction
Topics on atom - antiatom as basic constituents of the nature,have long held special fascination for scientific communities,and the interactions among their elements of fundamental particles such as nucleon (proton p,neutron n)and antinucleon (antiproton¯p,antineutron ¯n),has preoccupied researchers with great concerns. These particles are comparatively far more complex than some other basic components of the matter,like electron - antielectron,not only by reason of the internal structures (nucleon-antinucleon possess internal structures rather than the electron-antielectron),but also due to different types of interactions they involve,i. e. ,electron - antielectron can only participate weak and electromagnetic interactions (we ignore gravitational interaction),but besides that,nucleon-antinucleon can also take part in strong interaction[1,2]. In this article,we seek to address the issue pertinent to strong interaction delivered by renormalized infinite - order hybrid loop - chain propagators,to work out analytical expression of differential cross-section for the p¯p→p¯p reaction (elastic scattering of proton - antiproton),under the isospin-SU(2)coupling model in frame of quantum field theory,and crucial physical effects of radiative corrections are acquired.
SU(2)invariant coupling model[3]based on the symmetry of isospin,is the selected phenomenological theory underlying our work,to serve as the foundation for describing strong interaction between nucleon -antinucleon and neutral/charged pions(π0,π±).While,in usual applications of SU(2)model to deal with strong interaction among pions and nucleon –antinucleon in frame of quantum field theory,the perturbation theory is commonly carried out from low to higher orders. In fact,most previous studies were processed by only“low order”handlings or other approximative methods,and then non - ignorable distance to the sense of accurate description still remains subsistent. So,for problems in isospin-SU(2)model or other topics under quantum field theory,corrections of“Loops”in higher orders would be asked for improving accuracy,but at the same time,it usually brings extraordinarily intricate intermediate states and divergent troubles[4-6]. Consequently,it’s necessary to make use of renormalization techniques,e. g. ,the often applied scheme of Feynman Integrals[7]or other approximate realizations[8-13],to eliminate unphysical divergent quantity whilst to keep the renormalized physical finite quantity. However,the radiative corrections would still be tiny even if it could be given by various renormalization methods, notwithstanding,these subtle contributions actually present indispensible significance for in - depth exploring physical questions by advanced precision[14-18]. Despite the intricacy of renormalization process,it still could not absolutely guarantee the results’convergence even if renormalizations for all possible infinite -order loops are entirely accomplished[19],forasmuch as the quantum field theory perhaps would be only an asymptotic form of some other more thorough theorem[20]and we still lack sufficient sophistication for issues with very high order processes.
However,in numbers of special situations,we can also consider renormalizations involving some types of infinite high order corrections. E. g. ,the infinite order chain propagator proposed by Dyson[19,21],who is one of founders of renormalization theory,to supply effective way to contribute finite outcomes[22]. With this thinking in mind,some available radiative corrections had been achieved by earlier researches[23,24], and several theoretical predictions[25-27]had been pointed out which agree well with experimental data. Therefore,in this paper,we concentrate on a typical infinite high order hybrid loop-chain propagator (HLCP)of neutral pion (π0),and will“strictly”compute the analytical differential cross - section (DCS)of p¯p→p¯p reaction based on these HLCPs. Here the “strictly”means that,although it’s involving infinite order processes (consisting of hybrid p¯p and n¯n loops within the loop-chain propagators simultaneously),the total contribution of the HLCP can still be analytically summed by use of the series,and this use of HLCP for seeking“strict”DCS has never been accomplished by previous literatures for p¯p→p¯p which is one representative physical reaction of nucleon collision. Through this effective arrangement,we formulate detailed calculations to work out the exact form of Δ(k2)(the function of renormalized HLCP),and the dσ/dΩ (differential cross-section)of p¯p→p¯p reaction where the strong interaction is delivered by these infinite order HLCPs. Furthermore,relevant information of radiative correction is obtained by comparison between this chain DCS and the DCS with only tree propagator of pions. The result shows this exploration of p¯p→p¯p reaction utilizing renormalized infinite order HLCPs would not only yield the rationality of theoretical analysis and the validity of calculation,but also contribute useful academic reference for relevant researches on nucleon collision to demand enhanced accuracy.
2 Structure of hybrid loop - chain propagator in proton-antiproton elastic scattering
We adopt isospin SU(2)invariant coupling model[3]to study DCS ofreaction,and the corresponding interaction Lagrangian is:
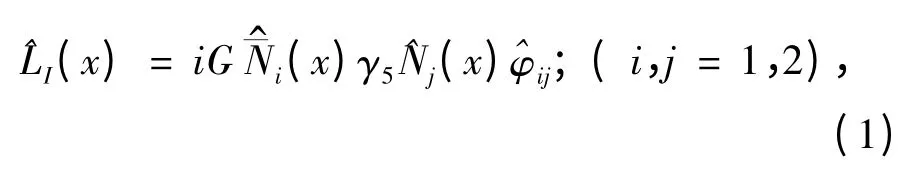
In this Lagrangian ^LI(x),proton and antiproton are treated as isospin doublets,and charged/neutral pions (π+,π-,π0)are described as isospin triplet and can be involved in the strong interaction. If only the tree-level Feynman diagrams of p¯p→p¯p reaction will be discussed,the intermediate process is simple(see Fig.1);but if we consider the situation with high order loop diagrams,the intermediate process could be quite complicated. In the perturbation theory under the frame of quantum field theory,conventionally it would be analyzed and renormalized order by order to compute the case with high order loop diagrams,however,this handling still cannot completely solve the calculation and renormalization problems of infinite high order loop diagrams covering all orders and all situations. For studying p¯p→p¯p reaction,here we utilize the scheme of loop-chain propagator founded by Dyson[19,21],to realize one special type of infinite high order loop -chain propagator (which partially contains propagators in all high orders in the manner of chains). Because we use the isospin SU(2)invariant coupling model,so this special infinite high order loop propagator will be formed into HLCP of neutral pion (propagator function is Δ(HLCP)F(k2)),which consists of both proton - antiproton loops and neutron-antineutron loops (see Fig.2).

Fig.1 Tree -level Feynman diagrams of p¯p→p¯p reaction, where the propagators ΔF(k2)in subfigure (a)and (b)are both tree propagators of π0(neutral pion)

3 Calculation of renormalized hybrid loop-chain propagator
From Fig.2,complicated internal structures of HLCPs of π0are lucidly delineated,with infinite processes of generation and annihilation of nucleon pairs. However,under the isospin-SU(2)invariant coupling model,analytical expressions of these infinite order HLCPs can still be worked out by corresponding summations of the geometric series (formed by the loops in different orders,see Figs. 2 and 3),and according to the schematic diagram in Fig.3 which intuitively clarifies the formation of the series,it’s not hard to calculate the function of HLCPs in the p¯p→p¯p reaction,as below:

Fig.2 Feynman diagrams for reaction with infinite order hybrid loop-chain propagators (HLCPs). The propagators(k2)in subfigures (a)and (b)are both infinite order hybrid loop-chain propagators of π0,and subfigure(c)demonstrates the detailed structure of the (k2)


4 Analytical expression of differential cross-section of proton -antiproton elastic scattering by infinite order hybrid loop-chain propagators
According to quantum field theory[3],the rela-tionship between cross-sectionand transition amplitudecan be written as:


We can convert discrete sum of Eq. (4)into continuous integral by the relation ∑→k→(V/(2π)3)∫d3→k. Here,spherical coordinate system is chosen and the direction of pole axis is identical to the direction of incident momentum,then with help of Eq.(5),we can simplify the DCS as follows:
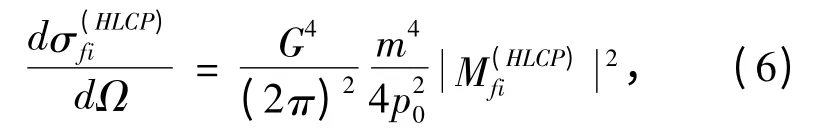
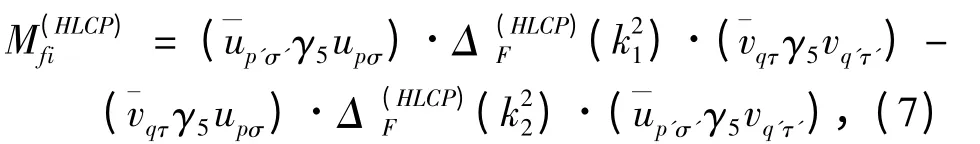

Further,it can be simplified by projection operator and properties of unit spinor of Fermion[3]as below:

Here,the T1,T2,T3,T4are traces with following forms:

Through lengthy works for Eq. (10)to (13)by trace technology[3],together with relations of= (p -p')2,= (p + q)2(conservation of four - momentum)and Eq. (6),the“strict”result of unpolarized DCS of pp¯→pp¯ scattering,where the strong interaction is delivered by renormalized infinite order HLCPs of neutral pions,can be analytically acquired:
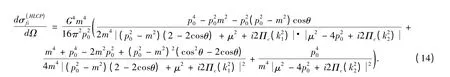

here,and the form of renormalized finite quantity ∏c(k2)of single loop is[28]:

If we set the ∏c(k2)into zero in Eqs. (2)and(3),i. e. ,these terms of f(k2)are changed into 1,then it’s not hard to find that the loop-chain propagators(k2)reduce back into tree propagators ΔF(k2). Therefore,through this replacement,Eq.(14)turns into unpolarized DCS with only tree-level propagators :

5 Analysis and discussion on the radiative corrections
For specific discussion on the effects of radiative corrections caused by HLCPs of neutral pions,Table 1 demonstrates radiative corrections with respect to incident energy and scattering angle.
Noticeable radiative corrections can be found inTable 1 and their quantities are all less than 1.0,with range of incident energy from 1000 Mev to 2000 Mev. This could bring corroborative information to suggest that the effect of radiative correction caused by HLCPs generally exists and should not be ignored,whilst the amounts of corrections yield to reasonable level. For intuitive representation,the relationships between DCS and scattering angle θ with comparisons between cases of chain propagator and tree - level propagator,are plotted in Fig.4 (a)to (f),given different incident energy from P0=1000 Mev,1200 Mev... ,to 2000 Mev respectively (here unit of vertical coordinates is Gev-2/Sterad,and unit of horizontal coordinates is radian). Explicit physical behaviors of radiative corrections in various conditions are apparently revealed in Fig.4,and the distinction no doubt reflects conspicuous difference between DCS with HLCP and DCS with only tree propagator. It is also shown that the overall DCS decays as incident energy goes up,implying the total cross - section would also fall with increasing incident energy,and consistent phenomenon can also be found in relevant study[27]grounded on photon chain propagators. In brief,the cases of HLCPs generally give evident and reasonable radiative corrections compared to the cases having only tree-level propagators,and all these results play supporting roles to argue that the considering of HLCPs is indispensable.
Table 1 Radiative corrections (defined as)caused by infinite order hybrid loop -chain propagators in ¯ reaction,against scattering angle θ and incident energy p0(Mev)
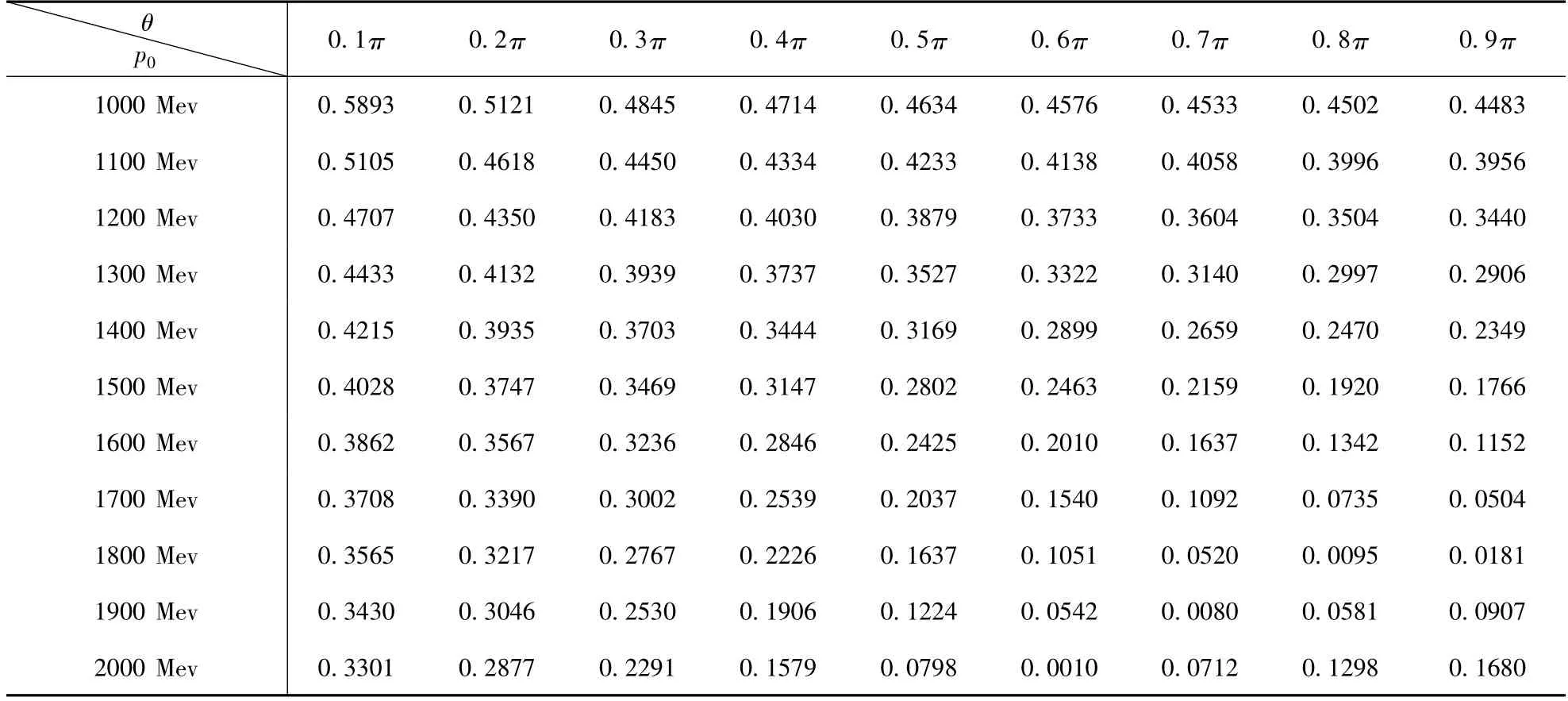
Table 1 Radiative corrections (defined as)caused by infinite order hybrid loop -chain propagators in ¯ reaction,against scattering angle θ and incident energy p0(Mev)
6 Summary and perspectives
Utilizing isospin - SU (2)invariant coupling model in frame of quantum field theory,unpolarized differential cross-section of proton -antiproton elastic scattering is achieved,with strong interaction delivered by infinite order hybrid loop -chain propagators of neutral pions (π0). Effective radiative corrections are addressed,by comparison of unpolarized differential cross -section between cases of hybrid loop-chain propagator and tree - level propagator. The analytical results for the infinite-high order processes obtained in this paper,could reflect the effect of radiative correction in“strict”manner with subtle information,and brings cogent affirmation of value of considering the hybrid loop-chain propagators. The outcomes would be referential to further investigations not only on isospin-SU(2)invariant coupling model or nuclear force,but also on theoretical or experimental researches related to proton collision,and especially it could add to our understanding of additional approaches towards renormalization of some infinite order radiative corrections.

Fig.4 Effect of radiative corrections demonstrated with comparison of unpolarized differential cross-sections of reaction between cases of infinite order hybrid loop-chain propagator (HLCP)and cases of tree propagator
Renormalization procedure is crucial to the effect of renormalized infinite -order loop -chain propagator in p¯p→p¯p reaction. Actually,as one of the most compelling and challenging topics in particle physics,renormalization theory has never stopped moving ahead,from its establishing which dates back to Dyson and other precursors[21,29],to theories appeared later such as renormalization for scalar meson-nucleon interactions given by Salam[30],convergence of renormalized integrals to any order of perturbation theory from Weinberg[31],renormalization of gauge invariant regulators proposed by ’t Hooft[32]and some other developments[33,34]. However,most current studies only tackle the renormalization within finite orders because the renormalization is still leaving many avenues of inquiry unexplored and many tough problems unanswered (e. g. intricate calculation,appropriate absorbing of renormalized finite quantities)in the context of phenomenological theory. Whereas,the renormalization method implemented in this article based on hybrid loop - chain propagators,not only takes the infinite order into consideration,but also suggests an effective and feasible approach to acquire convergent radiative correction. Besides,apart from this specific type of hybrid loop-chain propagator focused here,it’s not excluded any other propagators with further complicated structures and diverse components,although their convergence and availability of radiative correction should be concerned. The physical and mathematical arrangements employed here,can also be applied for other reactions,involving different class of propagators (e. g. photon chain propagators with renormalized single photon loop[35]),and else processes having variety of initial and final states. Moreover,we could extrapolate these implementations to alternative phenomenological scenarios even beyond the isospin - SU(2)model. All these interesting perspectives would be undertaken as potential studies in the future.
[1] Krisch A D. Proton -proton scattering and strong interactions[J]. Phys. Rev. Lett.,1963,11:217.
[2] Sakurai J J. Theory of strong interactions[J]. Annals of Physics,1960,11:1.
[3] Lurie D. Particles and fields[M]. New York:Interscience Publishers/John Wiley & Sons,1968.
[4] Jegerlehner F,Tarasov O V. Exact mass -dependent two- loop αs (Q2)in the background MOM renormalization scheme[J]. Nuclear Physics B,1999,549:481.
[5] Adkins G S,Fell R N,Sapirstein J. Two-loop renormalization of Feynman gauge QED[J]. Phys. Rev. D,2001,63:125009.
[6] Lee S Y. Higher-order corrections to leptonic processes and the renormalization of Weinberg's theory of weak interactions in the unitary gauge[J]. Phys. Rev.D,1972,6:1701.
[7] Itzykson C,Zuber J B. Quantum field theory[M].New York:McGraw-Hill Inc,1980:372.
[8] Li C S,Yang J M,Zhu Y L,et al. Yukawa corrections to top pair production in photon - photon collisions[J]. Phys. Rev. D,1996,54:4662.
[9] Ma W G,Li C S,Liang H. Yukawa corrections to charged Higgs-boson pair production in photon-photon collisions[J]. Phys. Rev. D,1996,53:1304.
[10] Liang H,Hu C G,Li C S,et al. Yukawa corrections to the bottom pair production in photon -photon collisions[J]. Phys. Rev. D,1996,54:2363.
[11] Matloob R. Mass renormalization in cavity QED[J].Phys. Rev. A,2011,83:012103.
[12] Abanov Ar,Chubukov A V. Spin-fermion model near the quantum critical point:One -loop renormalization group results[J]. Phys. Rev. Lett.,2000,84:5608.
[13] Chetyrkin K G,Rétey A. Renormalization and running of quark mass and field in the regularization invariant and MS schemes at three and four loops[J]. Nuclear Physics B,2000,583:3.
[14] Fang Z Y,Castro G L,Pestieau J,et al. Effective SU(2)L⊗U(1)theory and the Higgs boson mass[J].Mod. Phys. Lett. A,1997,12:1531.
[15] Denner A,Kraus E,Roth M. Physical renormalization condition for the quark - mixing matrix[J]. Phys.Rev. D,2004,70:033002.
[16] Greub C,Liniger P. Calculation of next -to -leading QCD corrections to b - >sg[J]. Phys. Rev. D,2001,63:54025.
[17] Kidonakis N,Owens J F. Effects of higher - order threshold corrections in high -ETjet production[J].Phys. Rev. D,2001,63:054019.
[18] Li Q,Jin L G,Li C S. Supersymmetric electroweak corrections to heavier top squark decay into a lighter top squark and neutral Higgs boson[J]. Phys. Rev.D,2002,66:115008.
[19] Dyson F J. Divergence of perturbation theory in quantum electrodynamics[J]. Phys. Rev.,1952,85:631.
[20] Zhu H Y. Quantum field theory[M]. Beijing:Science Press,1960:316 (in Chinese)
[21] Dyson F J. The radiation theories of Tomonaga,Schwinger,and Feynman[J]. Phys. Rev.,1949,75:486.
[22] Zhang Z C,Wang K J,Yi J M,et al. The accurate convergent formula and radiation correction of the renormalized π0and n-¯n chain propagator[J]. Journal of Chongqing University:Natural Science Edition,2007,30(11):117(in Chinese)[23] Wang X Y,Chen W S,Fang Z Y,et al. Accurate calculation of the differential cross - section of Compton scattering with electron renormalized chain propagator contribution[J]. Journal of Atomic and Molecular Physics,2008,25(2):335 (in Chinese)
[24] Pan Y,Wang K J,Fang Z Y,et al. Accurately calculate cross section of the n+¯n→2π0reaction in the n-¯n renormalization chain diagram [J]. Acta Phys.Sin.,2008,57(8):4817(in Chinese)
[25] Jiang M,Fang Z Y,Sang W L,et al. Accurate calculation of the differential cross section of Bhabha scattering with photon chain loops contribution in QED[J].Chin. Phys. Lett.,2006,23:2681
[26] Chen X W,Fang Z Y,Zhang J W,et al. Renormalization of two neutral mixing-loop chain propagators in standard model and its e+e-→μ+μ-cross section[J]. Acta Phys. Sin.,2011,60(2):020000(in Chinese)
[27] Chen X W,Fang Z Y,Jiang Z F,et al. Proton chain propagator that contains Fermi loops in W -S and its e-e+→μ-μ+cross section[J]. Journal of Atomic and Molecular Physics,2008,25(3):665 (in Chinese)
[28] Zhang Z C,Wang C M,Fang Z Y,et al. Effective method calculating the renormalized finite quantity of the meson loop propagator (II)[J]. Journal of Chongqing University:Natural Science Edition,2005,28(8):83(in Chinese)
[29] Hepp K. Proof of the Bogoliubov-Parasiuk theorem on renormalization[J]. Commun. Math. Phys.,1966,2:301.
[30] Salam A. Overlapping divergences and the S -Matrix[J]. Phys. Rev.,1951,82:217.
[31] Weinberg S. High -energy behavior in quantum field theory[J]. Phys. Rev.,1960,118:838.
[32] 't Hooft G. Renormalization of massless Yang -Mills fields[J]. Nuclear Physics B,1971,33:173.
[33] Bach V,Fröhlich J,Sigal I M. Renormalization group analysis of spectral problems in quantum field theory[J]. Advances in Mathematics,1998,137:205.
[34] Kostelecky V A,Lane C D,Pickering A G M. Oneloop renormalization of Lorentz - violating electrodynamics[J]. Phys. Rev. D,2002,65:056006.
[35] Zhang Z C,Gao F,Fang Z Y,et al. Strictly analytic calculation to the renormalized finite quantity of the photon loop (chain)propagator[J]. Journal of Chongqing University:Natural Science Edition,2005,28(11):101(in Chinese)
