多入单出正交空时分组码系统的调制识别

钱国兵李立萍 郭亨艺

(电子科技大学信息工程系 成都 611731)

多入单出正交空时分组码系统的调制识别

钱国兵*李立萍 郭亨艺

(电子科技大学信息工程系 成都 611731)

在现代无线通信系统中，采用正交空时分组码(STBC)的多天线发射技术是提高通信速率和可靠性，并且能够实现简单译码的关键技术。该文针对瑞利信道系统模型，提出一种适用于多入单出正交空时分组码(OSTBC)的调制识别算法。该算法通过对接收到的数据进行重排，将多入单出的系统模型转化为类似多入多出的系统模型，并且根据信源的特殊性用最大似然的思想实现调制类型的识别。仿真结果验证了所提算法的有效性。

无线通信；调制识别；多入单出；正交空时分组码

1 引言

多天线发射技术是现代无线通信中用来提高通信速率和可靠性的重要技术手段。空时分组码(Space-Time Block Code, STBC)[1−3]是多天线通信系统的主要编码方式，其中正交空时分组码因为能够提供满分集和译码简单被广泛使用。通信系统参数盲估计是一个重要的研究课题，广泛应用于军事及民用领域[4−6]，其中调制类型的盲识别具有重要的理论和现实意义，已引起国内外学者的关注。

2009年，Choqueuse等人[7]针对多入多出(MIMO)系统提出基于独立分量分析(ICA)的最大似然调制识别算法，该算法可以看作是在该系统下调制识别算法性能的上界，然而该算法只能适用于空分复用的情形却不能适用于空时分组码系统。2012年，Hassan等人[8]利用调制信号高阶累积量特征提出基于神经网络的识别算法，该算法能较好地适用于空间相关的信道模型，然而同样不能适用于空时分组码系统。同年，Mühlhaus等人[9]利用调制信号高阶累积量特征提出基于欧氏距离最小准则的识别算法。2013年，文献[10]在文献[9]基础上提出基于调制信号高阶累积量特征的最大似然识别算法，该算法计算复杂度远低于文献[7]提出的调制识别算法，然而同样不能适用于空时分组码系统。Luo等人[11,12]于2012年和2013年分别提出基于特征函数和多维ICA的最大似然调制识别算法，该算法能够较好地适用于空时分组码系统，然而只能有效地识别复调制(≥4PSK, ≥4QAM)，却不能适用于PAM等实调制类型。此外，这些方法都只能适用于多根接收天线的情形，目前还没有提出适用于多天线发射单天线接收情形下的调制识别算法。

本文针对正交空时分组码系统，提出一种适用于单根接收天线情形下的调制识别算法。首先，我们将接收到的数据进行重排，然后提出基于最大似然的调制识别算法。考虑到实际情形中信道是未知的，我们先用二阶统计量的方法[13]来预估信道，对于存在剩余模糊的编码，再用ICA算法中[14]帩度最大化的思想来去掉部分模糊，然后证明似然函数对剩余的模糊不敏感，因而可以用估计出来的信道进行调制识别。最后，仿真实验验证了本文算法的有效性。

2 系统模型

在正交空时分组码系统中，由星座M(假设其具有M个状态)调制后的每n个符号被分为一组，记为sv=[s1,s2,…,sn]T。向量sv被编码为一个nt×l(nt为发射天线个数，l为分组长度)维的复矩阵[3]：

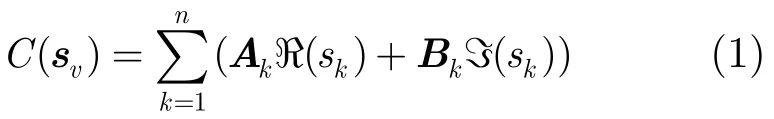
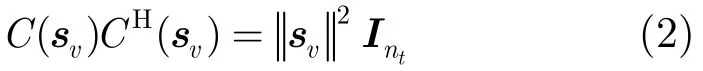
且满足：其中Ak和Bk均为nt×l维的空时编码矩阵，ℜ(·)和ℑ(·)分别表示取变量的实部和虚部。

空时分组码经天线发射后在只有单根接收天线情况下的信道传输模型为[3]

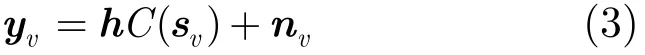
其中向量yv表示第v个组接收到的信号；向量h为信道传输向量，在本文中假设其为频率平坦衰落瑞利信道；nv为每个分组上的加性高斯白噪声，其在时间和空间上不相关；传输符号的功率假设是经过归一化的，即E(|sv|2)=1。这里需要声明的是，归一化的假设是很常见的，例如在参考文献[7-12]中。

3 基于最大似然的调制分类器

本文将yv的实部和虚部拼接为一个向量，则

其中vec(·)表示向量化。

为2l×2n维的虚拟信道矩阵。

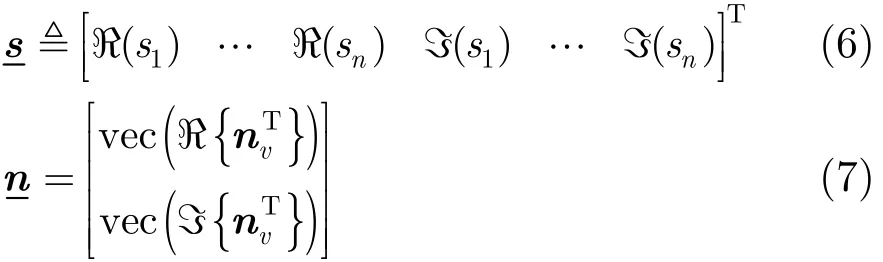
根据上述单个天线下的系统模型表达式，基于最大似然的调制类型识别可以表达为

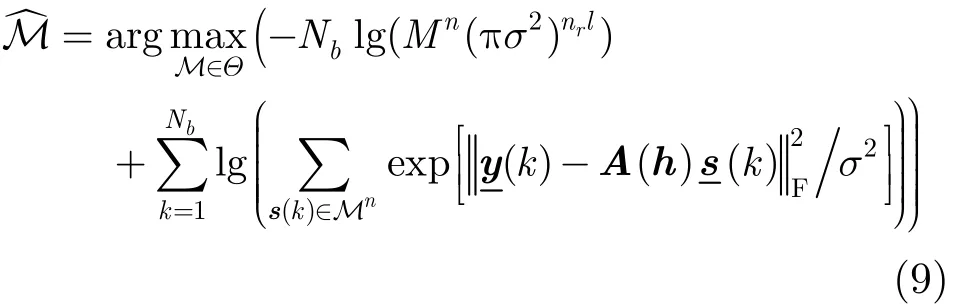
其中σ2表示噪声平均功率。

在实际场景中，信道信息往往是未知的。这里先利用正交空时分组码的特性用二阶统计量的方法[13]来预估信道(该方法只能适用于正交空时分组码是由于其依赖于编码的正交特性和特有的空时冗余)，对于存在剩余模糊的编码，再用帩度最大化的思想来去掉部分模糊。具体方法如下：

(1)如果ΦT(I2K⊗R)Φ的主特征值是m重的(m取值由具体的正交空时分组码决定[13])，那么=Uw，其中4nl×2nt维的矩阵Φ为h与vec{A(h)}之间的过渡矩阵，其第k列构造方式为vec{A(ek)}, ek为第k个元素为1而其余元素为0的2nt维的行向量，R为接收数据按式(4)重排后的自相关矩阵，U为主分量特征向量张成的空间，w=[w1… wm]T为待估实向量。此时，

由于大多数的数字调制(PAM,PSK,QAM)的帩度为负值[15]，所以最大化估计出来的源信号的帩度的绝对值等价于最小化估计出来的源信号的帩度。而sˆ由w决定，所以最小化sˆ帩度就等价于

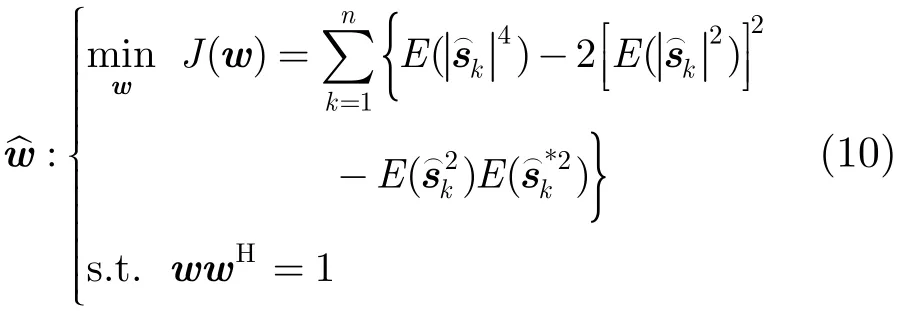
我们可以采用经典的梯度下降法来优化上面的代价函数，其中

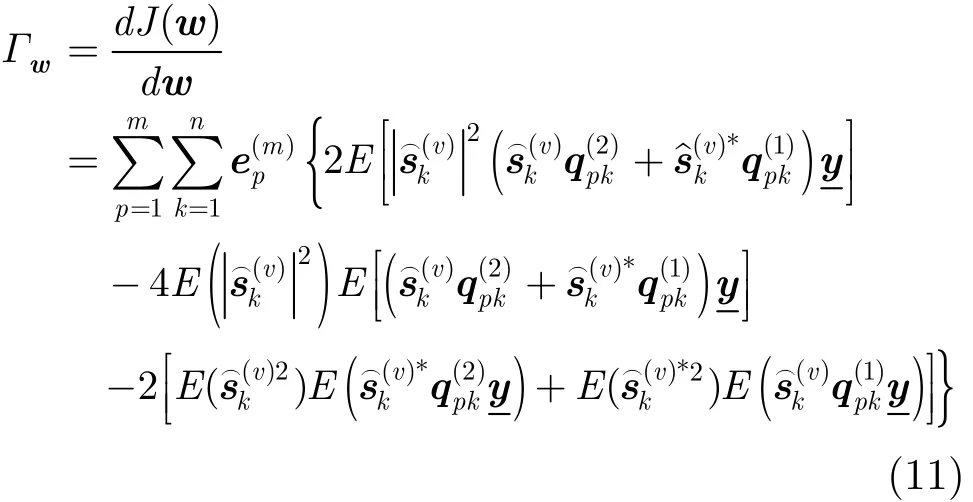
在无噪声情况下，估计出来的源信号和真实的源信号有一个置换，幅度，相位的模糊，即

其中D为对角矩阵，其对角线上元素分别为ejθ1,ejθ2,…,ejθn,P为交换矩阵。

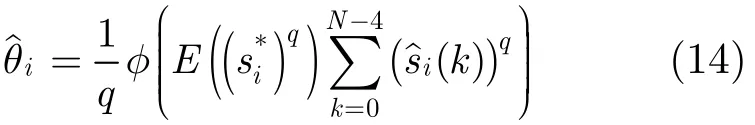
其中φ(·)表示取一个复数的相位角，系数q与调制类型有关，对于PAM调制，星座的旋转对称角度为π，所以q=2；对于M-PSK调制，q=M；对于正方形或矩形M-QAM调制，q=4。定义：为对角矩阵，其对角线上元素分别为,,…,;q为对角矩阵，其对角线上元素分别为ej2πρ1/q, ej2πρ2/q,…,ej2πρn/q，则D=q，其中q为剩余的相位模糊，ρ1,ρ2,…,ρn均为整数，取值范围为−(M −1)～(M−1),M为调制类型M的状态数。接下来，我们来证明似然函数对剩余的相位模糊并不敏感。

由式(13)可得

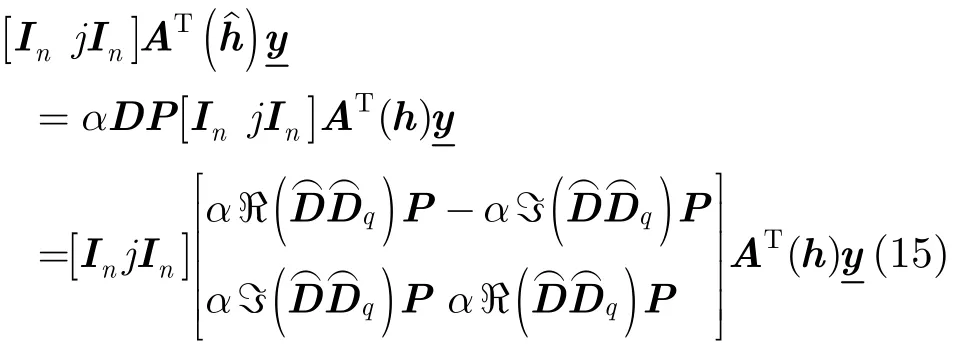
所以

此时的似然函数可以写成：

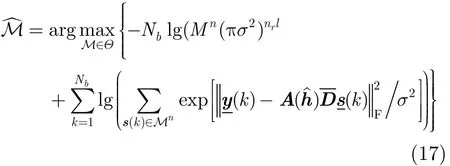
又由于s(k)∈Mn时，，因此似然函数可以进一步化简为

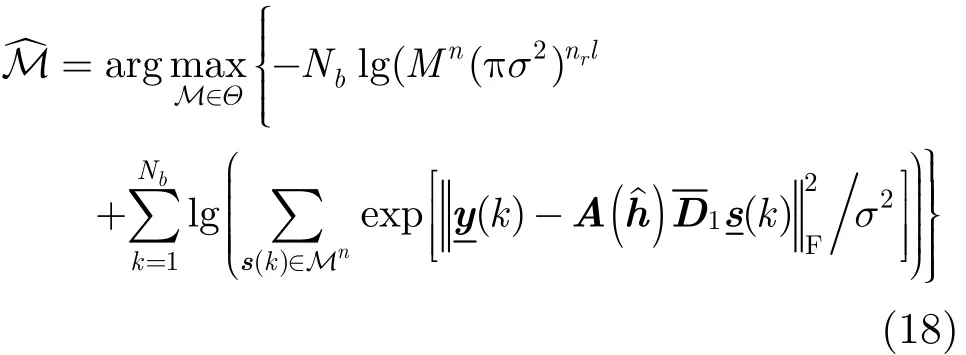
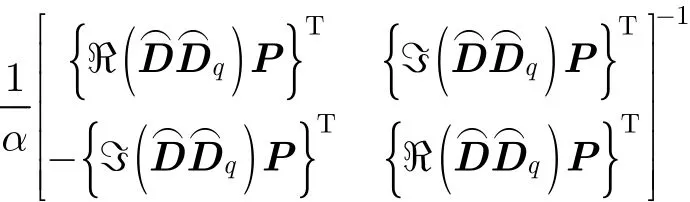
和

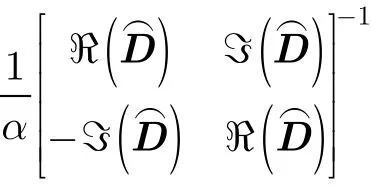
从以上证明过程中可以看出，似然函数对剩余的相位模糊并不敏感。

4 仿真

本文采用平均正确识别概率为指标来衡量算法性能，集合Θ由BPSK, 4PSK, 16PSK和16QAM 4种调制组成，所有仿真是在以下条件下进行：(1)瑞利信道；(2)噪声在空间和时间上不相关，方差为2σ；(3)单根天线接收，且接收到的空时分组码的组数Nb为512；(4)信噪比定义为[1,7]：SNR=10lg(P2/σ)，其中P为发射端天线总功率。在每个信噪比下进行500次蒙特卡洛仿真实验。

在仿真实验1和仿真实验2中分别采用Alamouti编码和3/4码率的正交空时分组码[3]，此外，为了避免梯度下降法收敛到局部极值，在估计信道时对w赋多个初值，最终收敛时使代价函数最小的w值即认为是使代价函数收敛到全局极值的w。

仿真实验1 多入单出系统采用Alamouti编码时的正确识别概率

图1是多入单出(MISO)系统采用Alamouti编码时本文所提出的调制识别算法的性能曲线。图1(a)是发射端符号采用BPSK调制时的识别概率，从中可以看出，当信噪比大于或等于1 dB时正确识别的概率能达到100%，而在低信噪比下，可能会将调制类型误识别为QPSK或者16QAM；图1(b)是发射端符号采用QPSK调制时的识别概率，从中可以看出当信噪比大于或等于7 dB时，正确识别的概率能达到100%，而在低信噪比下，容易将调制类型误识别为16QAM；图1(c)是发射端符号采用16PSK调制时的识别概率，从中可以看出当信噪比大于或等于7 dB时，正确识别的概率能达到100%，而在低信噪比下，容易将调制类型误识别为QPSK或者16QAM；图1(d)是发射端符号采用16QAM调制时的识别概率，从中可以看出当信噪比大于或等于7 dB时，正确识别的概率能达到100%，而在低信噪比下，容易将调制类型误识别为QPSK。

仿真实验2 多入单出系统采用3/4码率的正交空时分组码的正确识别概率

图2是多入单出系统采用3/4码率的正交空时分组码时本文所提出的调制识别算法的性能曲线。图2(a)是发射端符号采用BPSK调制时的识别概率，从中可以看出当信噪比大于或等于1 dB时，正确识别的概率能达到100%，而在低信噪比下，容易将调制类型误识别为QPSK；图2(b)是发射端符号采用QPSK调制时的识别概率，从中可以看出当信噪比大于或等于5 dB时，正确识别的概率能达到100%，而在低信噪比下，容易将调制类型误识别为16QAM；图2(c)是发射端符号采用16PSK调制时的识别概率，从中可以看出当信噪比大于或等于5 dB时，正确识别的概率能达到100%，而在低信噪比下，容易将调制类型误识别为QPSK或者16QAM；图2(d)是发射端符号采用16QAM调制时的识别概率，从中可以看出当信噪比大于或等于3 dB时，正确识别的概率能达到100%，而在低信噪比下，容易将调制类型误识别为QPSK。对比图1可以看出，本文所提出的调制识别算法在系统采用3/4码率的正交空时分组码时性能要优于采用Alamouti编码时的性能。

5 结束语

本文提出一种适用于多入单出正交空时分组码系统的调制识别算法。首先，利用正交空时分组码在时间和空间上的特殊冗余性，将多入单出系统模型转换为多入多出的系统模型。然后在该模型上利用等效信源的特殊性，提出了基于最大似然的调制识别算法。仿真结果验证了本文算法的有效性。

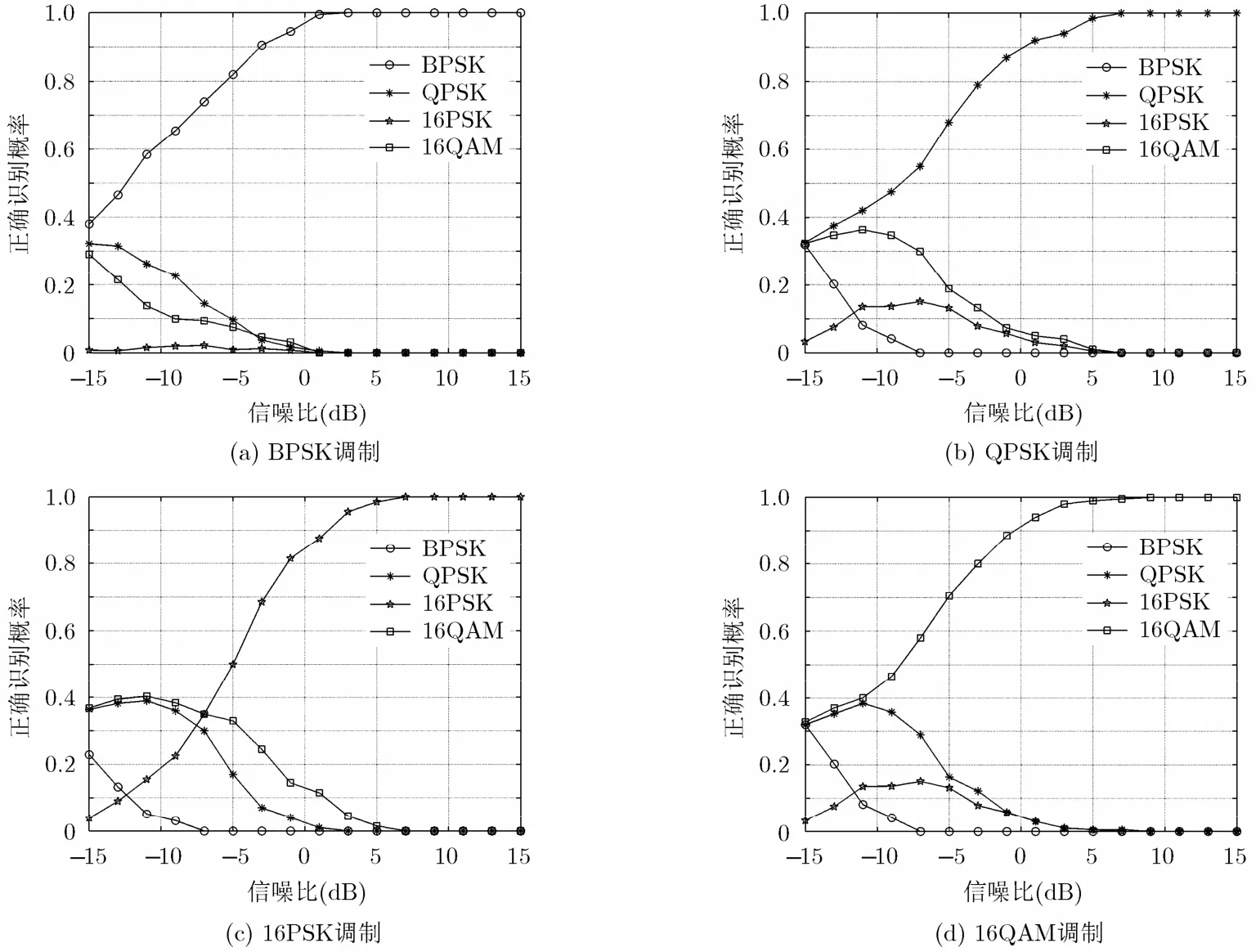
图1 多入单出系统采用Alamouti编码时各种调制类型的正确识别概率

图2 多入单出系统采用3/4码率的正交空时分组码时各种调制类型的正确识别概率

[1] Vucetic B and Yuan J. Space-time Coding[M]. New York: John Wiley & Sons, 2003, Chapters, 3-5.

[2] Jafarkhani H. Space-time Coding: Theory and Practice[M]. New York: Cambridge University Press, 2005: 45-53.

[3] Larsson E G and Stoica P. Space-time Block Coding for Wireless Communications[M]. New York: Cambridge University Press, 2008: 79-95.

[4] 付卫红, 杨小牛, 刘乃安. 基于四阶累积量的稳健的通信信号盲分离算法[J]. 电子与信息学报, 2008, 30(8): 1853-1856. Fu Wei-hong, Yang Xiao-niu, and Liu Nai-an. Robust algorithm for communication signal blind separation fourthorder-cumulant-based[J]. Journal of Electronics & Information Technology, 2008, 30(8): 1853-1856.

[5] 李进, 冯大政, 房嘉奇. MIMO 通信系统中 QAM 信号的快速半盲均衡算法研究[J]. 电子与信息学报, 2013, 35(1): 185-190. Li Jin, Feng Da-zheng, and Fang Jia-qi. Study of fast semi-blind equalization algorithm for MIMO systems with QAM signal[J]. Journal of Electronics & Information Technology, 2013, 35(1): 185-190.

[6] Qian G, Li L, Luo M, et al.. Blind recognition of space-time block code in MISO system[J]. EURASIP Journal on Wireless Communications and Networking, 2013, 164(1): 1-12.

[7] Choqueuse V, Azou S, Yao K, et al.. Blind modulation recognition for MIMO systems[J]. MTA Review, 2009, 19(2): 183-196.

[8] Hassan K, Dayoub I, Hamouda W, et al.. Blind digital modulation identification for spatially-correlated MIMO systems[J]. IEEE Transactions on Wireless Communications, 2012, 11(2): 683-693.

[9] Mühlhaus M S, Öner M, Dobre O A, et al.. Automatic modulation classification for MIMO systems using fourth-order cumulants[C]. Vehicular Technology Conference (VTC Fall), Quebec City, 2012: 1-5.

[10] Muhlhaus M, Oner M, Dobre O, et al.. A low complexity modulation classification algorithm for MIMO systems[J]. IEEE Communications Letters, 2013, 17(10): 1881-1884.

[11] Luo M, Li L, and Tang B. A blind modulation recognition algorithm suitable for MIMO-STBC systems[C]. International Conference on Communications and Information Technology (ICCIT), Chengdu, 2012: 271-276.

[12] Luo M, Li L, Qian G, et al.. A blind modulation identification algorithm for STBC systems using multidimensional ICA [J]. Concurrency and Computation: Practice and Experience, 2013, 26(8): 1490-1505.

[13] Shahbazpanahi S, Gershman A B, and Manton J H. Closed-form blind MIMO channel estimation for orthogonal space-time block codes[J]. IEEE Transactions on Signal Processing, 2005, 53(12): 4506-4517.

[14] Comon P and Jutten C. Handbook of Blind Source Separation: Independent Component Analysis and Applications[M]. Oxford: Academic Press, 2011: 179-226.

[15] Swami A and Sadler B M. Hierarchical digital modulation

classification using cumulants[J]. IEEE Transactions on Communications, 2000, 48(3): 416-429.

[16] Moeneclaey M and De Jonghe G. ML-oriented NDA carrier synchronization for general rotationally symmetric signal constellations[J]. IEEE Transactions on Communications, 1994, 42(8): 2531-2533.

钱国兵： 男，1986年生，博士生，研究方向为盲源分离、通信信号处理.

李立萍： 女，1963年生，教授，博士生导师，主要研究方向为非合作信号处理、高速信号处理、微弱信号检测与参数估计等.

郭亨艺： 女，1989年生，硕士生，研究方向为通信信号处理.

Modulation Identification for Orthogonal Space-time Block Code in Multiple Input Single Output Systems

Qian Guo-bing Li Li-ping Guo Heng-yi
(Department of Information Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)

In modern wireless communication systems, multiple-antenna-transmitting in association with Orthogonal Space-Time Block Code (OSTBC) is a key technology to improve communication rate, reliability, and decoding complexity. In this paper, a modulation identification algorithm is proposed which is well suitable for the Multiple Input Single Output (MISO)-OSTBC system. First, the MISO system is transformed into a Multiple Input Multiple Output (MIMO) system by reshaping the

data. Then, maximum likelihood based approach is used to identify the modulation. Simulations validate the effectiveness of the proposed algorithm.

Wireless communication; Modulation identification; Multiple Input Single Output (MISO); Orthogonal Space-Time Block Code (OSTBC)

TN92

： A

：1009-5896(2015)04-0863-05

10.11999/JEIT140644

2014-05-14收到，2014-12-26改回

通信信息控制和安全重点实验室基金(9140C130304120C13064)和国家自然科学基金(61201282)资助课题

*通信作者：钱国兵 shuaiguobing@hotmail.com