弹载合成孔径雷达大斜视子孔径频域相位滤波成像算法

李震宇梁 毅 邢孟道 保 铮

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

弹载合成孔径雷达大斜视子孔径频域相位滤波成像算法

李震宇*梁 毅 邢孟道 保 铮

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

弹载合成孔径雷达(SAR)为满足机动性和实时性，常采用大斜视子孔径成像处理；而大斜视SAR成像存在严重的距离方位耦合，时域校正距离走动解决这一问题会带来方位聚焦深度问题。针对方位聚焦深度问题以及子孔径特性，该文提出一种新的子孔径成像算法—频域相位滤波算法(FPFA)，该算法在无近似瞬时斜距模型下，采用时域校正距离走动，频域校正弯曲，在方位频域引入相位滤波因子校正多普勒调频率和方位向高次项的空变性，并结合谱分析(SPECAN)技术实现方位聚焦。仿真和实测数据处理验证了该算法的有效性。

弹载合成孔径雷达；子孔径；大斜视；频域相位滤波算法；谱分析技术

1 引言

随着合成孔径雷达(Synthetic Aperture Radar, SAR)成像技术的发展，将SAR与精确制导技术相结合的弹载SAR已成为近年的研究热点[1,2]。在军事上，弹载SAR通常在侦查完后还需完成攻击，为了保证导弹具备一定的转弯机动时间，弹载SAR一般需在大斜视的情况下成像。而由于弹载SAR天线尺寸较小，其全孔径方位分辨率一般远高于匹配参考图，为了保证后续景象匹配、弹体定位等一系列处理正常进行和满足制导率的需要，以修正惯性导航系统(Inertial Navigation System, INS)误差为目的的弹载SAR成像算法不宜太过复杂，可在适当损失分辨率的代价下仅使用子孔径数据进行相干处理，尽可能简化处理流程、减小运动补偿复杂度、计算量和存储量，以实现快视成像。因此，对于子孔径弹载SAR大斜视成像算法的研究具有重大意义。

针对斜视SAR成像，人们提出多种算法(大斜视子孔径(High Squint Subaperture, HSS)[3,4]，波数域(Omega-K)[5−7]， 非线性变标(NonLinear Chirp Scaling, NLCS)[8−12]，极坐标格式算法(Polar Format Algorithm, PFA)[13]等)以及一系列的改进算法(扩展非线性变标(Extended Nonlinear Chirp Scaling, ENLCS)[14]，改进非线性变标 (Modified Nonlinear Chirp Scaling, MNLCS)[15]，恒加速波数域(Constant Acceleration Omega-K, CA Omega-K)[16]等)。这些算法提高了斜视SAR成像精度，但都有自身的缺点。其中HSS首先引入线性距离走动因子来降低距离方位的耦合度，但是并未解决由此带来的方位聚焦深度问题，而且HSS算法成像精度受限于子孔径重叠比影响；Omega-K与PFA受制于复杂而低效的插值，并不适用于实时成像需求较高的弹载SAR。NLCS在一定程度上解决了大斜视中调频率空变问题；ENLCS和MNLCS在NLCS的基础上进一步修正了操作精度，扩展了大斜视方位幅宽；但这些算法均是基于全孔径处理，无法直接用于子孔径，而弹载SAR从实际应用需要出发，采用子孔径成像更具优势。

本文针对弹载SAR子孔径数据，提出无近似瞬时斜距模型，详细分析了时域走动校正所带来的方位空变特性，并根据子孔径数据特性提出一种基于频域相位滤波处理的方位空变校正新方法，适用于子孔径大斜视宽幅成像；最后通过点目标仿真以及实测数据处理验证了本文所提算法的有效性和实用性。

2 无近似瞬时斜距模型

弹载SAR大斜视成像几何模型如图1所示，雷达工作在条带模式，平台高度为h，以速度v沿X轴匀速直线飞行，波束射线指向的斜视角为θ0，令R0为波束中心线扫过目标时的斜距；场景中某一点目标与雷达的最近距离为RB。由图1的几何关系可知，点目标到雷达的瞬时斜距为

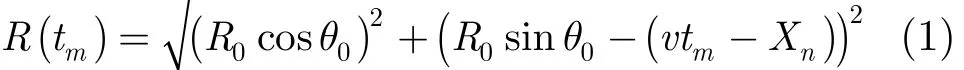
其中，tm为方位慢时间，xn=vtn,tn为天线波束中心穿越目标点的时刻。

通常情况下，为简化成像处理将式(1)作泰勒展开，将包络近似到方位慢时间的二次项，相位近似到方位慢时间的三次项[8−12]，但在弹载大斜视或方位幅宽较宽的情况下，采用这种近似将会带来较大的剩余包络误差和相位误差，对应的包络误差和相位误差分别为

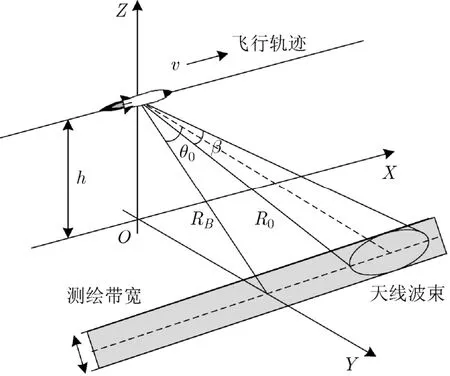
图1 弹载SAR大斜视几何模型

ΔRe=R(tm;R0)

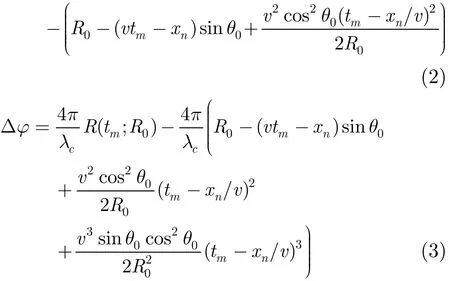
其中λc为载波波长。这里以表1所示的弹载SAR参数分析来说明，则由近似带来的包络剩余误差和相位剩余误差如图2所示。

表1 雷达参数

由图2可见，边缘位置包络近似相对误差在3 m左右，根据包络误差小于四分之一个距离分辨单元可以忽略的准则，此时的距离分辨率不能高于12 m；而剩余相位误差远大于π/4，严重影响成像质量。对于弹载SAR大斜视情况，由于弹载SAR系统载频较高、速度快等特点，传统算法中对包络采用方位慢时间的二阶近似，对相位采用方位慢时间的三阶近似，会有较大的包络和相位残留；这部分残留相位会严重影响成像质量；因此针对弹载SAR的研究需要考虑更高阶的近似模型。本文针对弹载SAR成像采用无近似的瞬时斜距模型。

3 距离向处理

假设雷达发射信号为线性调频(Linear Frequency Modulation, LFM)信号，则基频回波可以写为

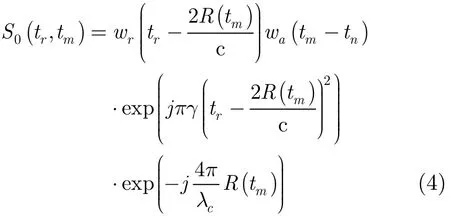
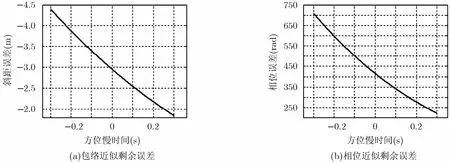
图2 包络和相位剩余误差分析

其中，tr为距离快时间，c为光速，γ为发射信号的调频率，λ为雷达中心波长，wr(·)表示发射信号的窗函数，wa(·)表示方位窗函数。对式(4)作距离向傅里叶变换，将其变换到距离频域为

Ss(fr,tm)=Wr(fr)wa(tm−tn)

其中，fr为距离频率，fc为雷达中心载频，wr(·)为距离窗函数的频域形式。

斜视SAR由于存在较大的线性距离走动，导致距离向与方位向之间具有较强的耦合，时域线性距离走动校正可以极大地降低这种耦合性[8−12]。因此，首先进行线性距离走动校正，校正函数为

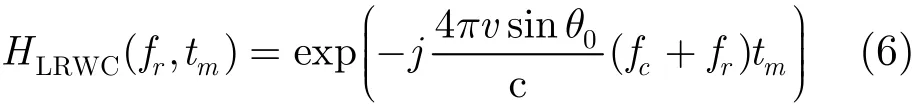
式(6)与式(5)相乘并作距离向脉冲压缩，可得Ss(fr,tm)=Wr(fr)wa(tm−tn)

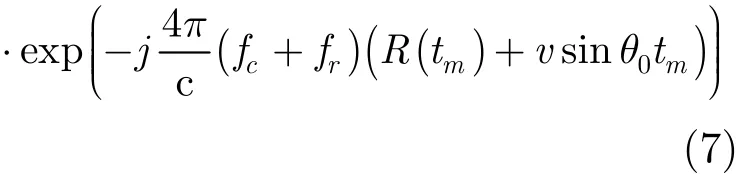
采用驻定相位原理，对式(7)作方位向傅里叶变换将其变换到2维频域，可得

SS(fr,fa)=Wr(fr)Wa(fa)

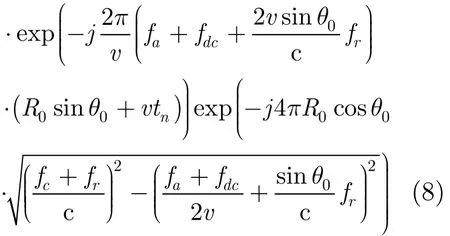
其中fa为方位频率，Wa(·)为方位窗函数的频域形式，fdc为多普勒中心频率，且fdc=2vsinθ0/λ。为了进一步分析距离弯曲特性，将式(8)中根号中的项在fr=0处进行泰勒展开，并近似到距离频率的二次项，得

由信号的徙动特性可知，式(9)中Bfr所对应的相位为距离徙动校正项，C所对应的相位为二次距离压缩项；将补偿完距离徙动以及二次距离压缩后的信号变换到距离时域，可以得到经过距离向处理后的信号

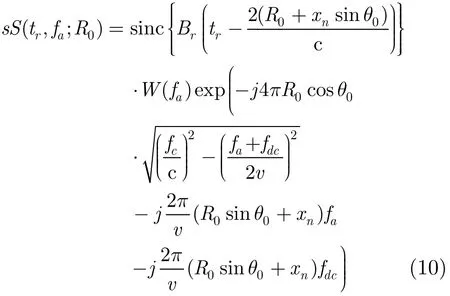
式(10)中R0+xnsinθ0为经过距离向处理后的目标位置，可以发现，此时目标距离向位置将不再是R0，而是一个随方位位置xn变化的量，这意味原本位于同一距离单元内的3点A,B和C，在时域校正线性走动后，点A被移到R0+x−nsinθ0的位置，而点C被拉到位于R0+xnsinθ0的位置，如图3所示；即时域校正线性走动后，对于距离单元相同而方位位置不同的点目标，将出现在不同的距离单元内，这导致了距离向的几何形变及多普勒调频率的方位空变性、方位向高次项的空变，方位向将不再具有平移不变性，这就是方位聚焦深度的本质。

4 基于频域相位滤波处理的方位向聚焦分析

观察式(10)，经过距离向处理后的回波信号包络为sinc函数，并且目标位于R0+xnsinθ0处。这里引入变量代换，令

图3 时域线性走动校正示意图

对式(10)在fa=0处进行泰勒展开，并近似到fa的五次项得

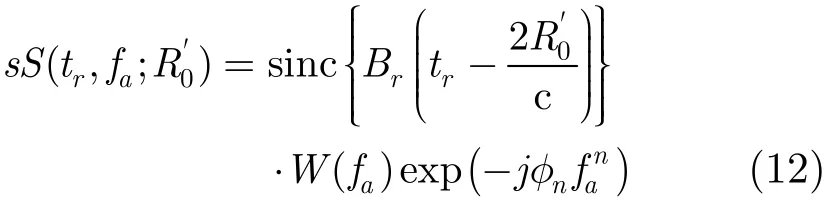
其中

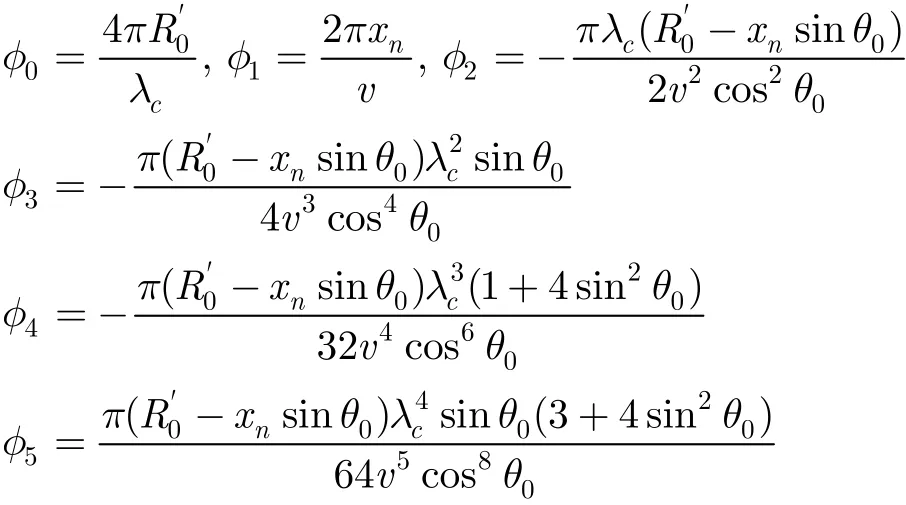
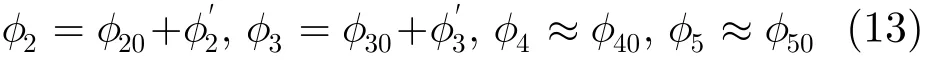
其中φn0为非空变部分，为空变部分。

补偿方位非空变的高次相位，相位补偿函数为

将经过高次相位补偿后的信号变换到方位时域，得

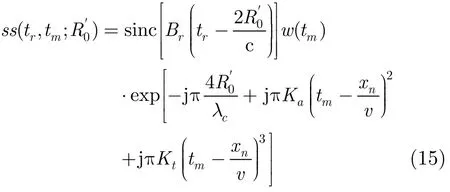
其中Ka为多普勒调频率，Kt为三次项系数，且

式(16)相当于对方位调频率进行关于方位位置的二阶近似，对三次项系数进行关于方位位置的一阶近似，现有方法通常只对调频率进行方位位置的一阶近似[8−12]，在斜视角较大或者方位幅宽较宽时，采用式(16)的近似具有更高的近似精度。

4.1 频域相位滤波校正方位空变

由于弹载SAR采用子孔径处理，原先针对全孔径处理的算法失效，无法直接运用于子孔径处理；通过时频分析全孔径与子孔径特性(以3个点目标为例，Tsub表示子孔径时间)，如图4(a)所示，全孔径对应的时频分布线在时间轴的投影是相互错开的，因此针对全孔径处理可以在时域引入滤波因子(变标因子)校正调频率空变，如常规的方位NCS算法；而对于子孔径数据，如图4(a)到图4(b)，其时频分布线在时间轴的投影是相互重叠在一起的，无法直接在时域引入滤波因子校正方位调频率的空变；图4(c)中将子孔径数据变到频域时，相当于时频轴翻转，场景中各点数据支撑区相互分开，这时的时频分布等效于全孔径时域分布特性，因此可以在频域引入滤波因子校正方位调频率空变。

进一步分析：此时三点所对应的相位分布线在时域重叠在一起的且相位曲线曲率不同(存在空变)，如图5(a)所示；将数据变换到频域后，频域的相位曲线是错开的，因此可以想到在频域通过叠加另一个相位因子，将频域原先错开、具有不同形状的相位变化率曲线修正成一样，进而利用统一的聚焦因子进行方位聚焦处理，如图5(b)和图5(c)所示，整个处理过程称之为频域相位滤波。

4.2 方位统一聚焦处理

由第4.1节分析可得，引入频域相位滤波因子形式可写为

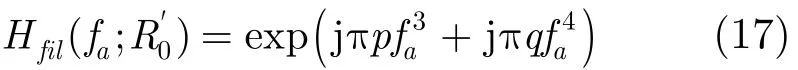
其中p,q为待定量。将经过高次相位补偿后的式(12)与式(17)相乘，将结果变换到方位时域，得

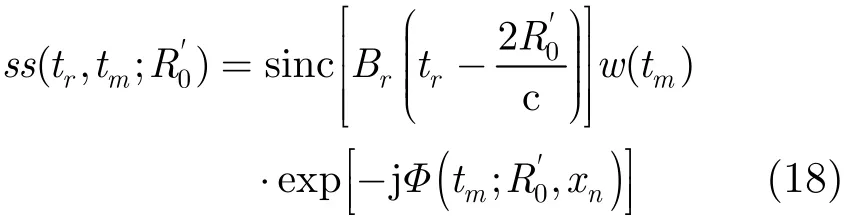
其中

图4 子孔径信号特性分析

图5 频域相位滤波校正方位空变示意图

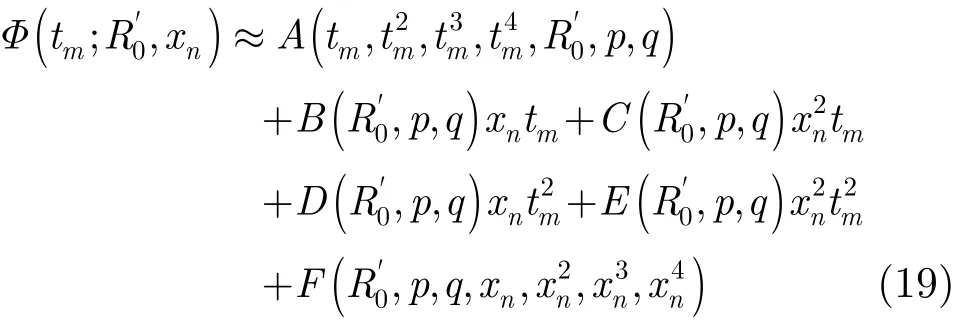
分析式(19)中的各个相位项：第1项为方位调制项，该项与目标方位位置无关，可以进行统一的补偿；第2项为目标方位位置与tm一次项的耦合项，反应目标点的方位位置；第3项为目标方位位置的偏差项，由于是方位位置平方项与tm一次项的耦合项，会造成目标方位位置偏差方向左右一致，且目标偏离场景中心越远，方位偏差越大，该项可以通过后续的投影来校正。第4项、第5项是影响成像聚焦性能的关键相位，均与目标方位位置xn有关，为空变的方位调制相位，造成方位无法统一聚焦成像，且第4项和第5项反映了调频率随方位位置的一阶和二阶空变，以及时域三次项系数随位置的空变特性；第6项为剩余的与方位慢时间tm无关的相位项，该项对方位聚焦没有影响，通常可以忽略。为消除空变的方位调制项，令D(R'0,p,q)=0, E(,p,q)=0，即建立方程组

求解该方程组，可以得到

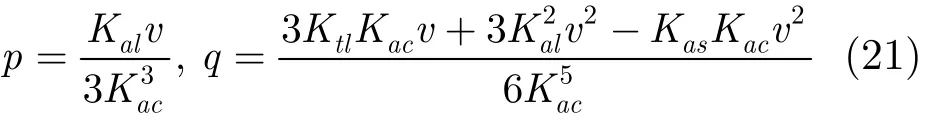
进一步，将求得的p,q代入A,B,C表达式中，可得A中关于tm的三次项和四次项为频域乘以扰动相位在时域引入的高次相位，为需要补偿的残余高次相位；并对信号乘以方位Deramp函数，并作方位FFT，可以得到聚焦后的两维图像。其中相应的补偿函数和Deramp参考函数即为方位统一聚焦因子

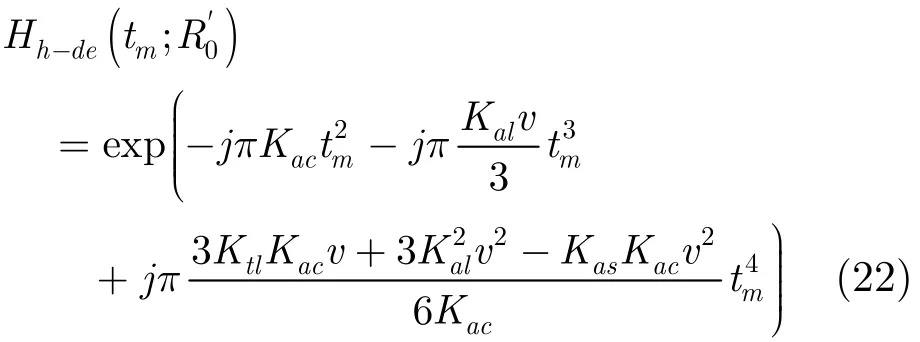
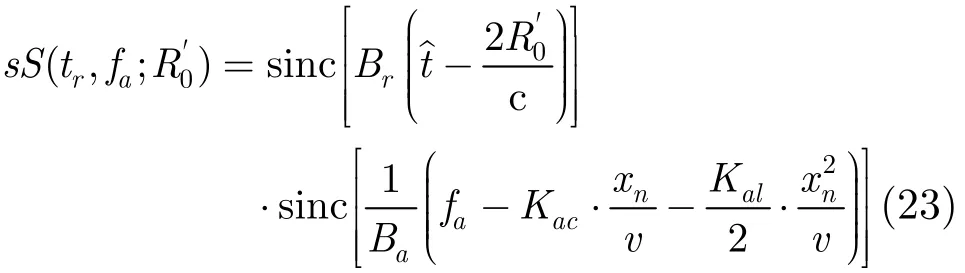
两维聚焦后的图像为式(23)中，Ba为单个点子孔径数据对应的方位多普勒带宽。综上所述，整个算法流程图如图6所示。从图6的整个处理流程图可以看出，本文提出的子孔径成像算法只包含复乘和FFT运算，不涉及插值处理，因此易于工程实现。

5 数据处理结果与分析

为了验证本文所提算法的有效性，下面通过对仿真数据和实测数据处理来进行说明。

弹载SAR系统仿真参数如表1所示。地面场景中沿弹体飞行方向放置3个点目标，记为pn(n= 1,2,3)，如图7所示，点目标两两间距6000 m，沿弹体飞行方向张成的距离为12 km，场景中心线对应的作用距离为30 km，斜视角θ0为80o，地平面投影角θ为87o。

图6 弹载SAR子孔径大斜视成像算法流程图

图7 点目标布置示意图

为了更好地反映成像聚焦性能，以边缘点p1, p3和中心点p2的成像结果进行分析。图8给出了传统方法的子孔径成像方位脉冲压缩剖面图[8−12]，由于忽略了调频率随方位位置的二阶空变和三次相位系数随方位位置的空变，因此边缘点第1零点抬高，造成积分旁瓣比损失，第1旁瓣抬高，造成峰值旁瓣比损失，影响方位分辨率。图9给出了本文方法的成像方位向剖面图，由于同时考虑调频率随方位位置一阶、二阶空变，以及三次相位系数随方位位置的空变，此时第1旁瓣和第1零点均得到拉低，且脉冲压缩剖面图接近中心点方位脉冲压缩剖面图。图10给出了采用本文方法对三点成像结果的2维等高线图，从等高线图中可以看出主瓣、副瓣明显分开且呈现良好的“十字架”状。

为评估本文提出算法的性能，计算p1,p2和p3的分辨率、峰值旁瓣比、积分旁瓣比指标参数如表2所示，可以看出，传统方法所得指标与理论值(方位分辨率2 m，峰值旁瓣比-13.26 dB，积分旁瓣比-9.8 dB)有着一定的偏差；分辨率、峰值旁瓣比以及积分旁瓣比都较差，而本文方法所得性能指标参数与理论值基本吻合，说明本文算法的有效性。

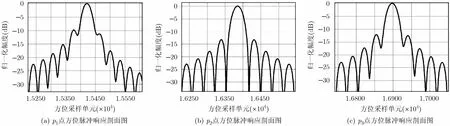
图8 传统方法成像结果的方位脉冲响应剖面图

图9 本文算法成像结果的方位脉冲响应剖面图

图10 本文算法成像结果的等高线图

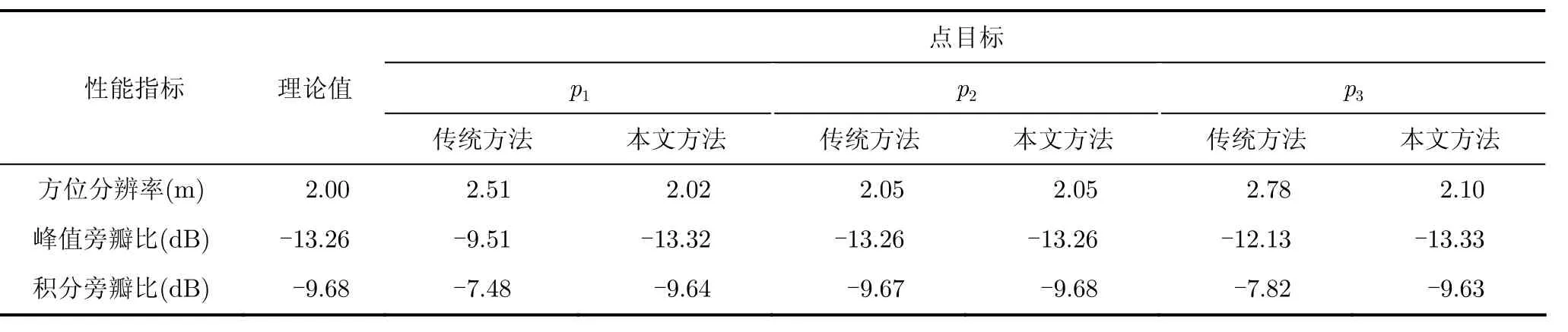
表2 成像性能分析

为进一步验证算法的有效性，采用本文算法对某机载实测数据进行处理，雷达系统工作在Ku波段，斜视角度约为60o，场景大小约为3 km×1 km(沿雷达视线方向×垂直雷达视线方向)，图11(a)为实测数据成像结果，整个场景地貌特征明显，聚焦效果良好；采用方位向不同处理方法，并选取方位向边界处作为对比比较(图11(a)中虚线框)，图11(b)和图11(c)分别给出了不同的处理结果，其中图11(b)为传统方法的结果，其聚焦效果较差；图11(c)给出本文方法成像结果，可以看出图11(c)中边缘点成像聚焦效果比图11(b)有着显著地提升，验证了本文算法的有效性。

图11 机载子孔径大斜视实测数据结果

6 结束语

本文针对弹载SAR大斜视子孔径成像问题，提出一种频域相位滤波的子孔径成像方法。根据弹载SAR大斜视成像几何模型，给出无近似瞬时斜距模型，基于无近似斜距表达式，推导距离走动校正因子和距离弯曲校正因子，并分析时域距离走动校正带来的影响。针对方位向处理，详细分析走动校正带来的方位频率二次、三次相位系数随方位位置的空变特性。为了实现空变补偿与聚焦，根据子孔径数据特性提出一种基于频域相位滤波的方位统一处理方法，其创新思想是针对子孔径数据时域混叠频域错开的特性，通过频域引入相位滤波因子，来校正时域调频率以及三次相位随方位位置的空变特性。最后基于谱分析处理实现方位的聚焦成像。整个算法只包含复乘和FFT运算，不涉及插值处理，易于工程实现。点目标仿真数据和机载实测数据处理验证了本文提出算法的有效性和实用性。

[1] 周鹏, 周松, 熊涛, 等. 基于级数反演的弹载SAR下降段CZT成像算法[J]. 电子与信息学报, 2010, 32(12): 2861-2867.

Zhou Peng, Zhou Song, Xiong Tao, et al.. A chirp-Z imaging algorithm for missile-borne SAR with diving maneuver based on the method of series reversion[J]. Journal of Electronics & Information Technology, 2010, 32(12): 2861-2867.

[2] 周松, 杨磊, 周鹏, 等. 基于双曲线修正斜距模型的弹载SAR成像方法[J]. 系统工程与电子技术, 2013, 35(6): 1168-1176.

Zhou Song, Yang Lei, Zhou Peng, et al.. Imaging method for missile-borne SAR based on model of hyperbolic slant range with linear modifying[J]. Systems Engineering and Electronics, 2013, 35(6): 1168-1176.

[3] Sun Xiao-bing, Yeo Tat-soon, Zhang Cheng-bo, et al.. Time-varying step-transform algorithm for high squint SAR imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(6): 2668-2677.

[4] Yeo Tat-soon, Tan Ngee-leng, Zhang Cheng-bo, et al.. A new subaperture approach to high squint SAR processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(5): 954-968.

[5] Xiong Tao, Xing Meng-dao, Xia Xiang-gen, et al.. New applications of omega-K algorithm for SAR data processing using effective wavelength at high squint[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(5): 3156-3169.

[6] Liu Yan, Xing Meng-dao, Sun Guang-cai, et al.. Echo model analyses and imaging algorithm for high-resolution SAR on high-speed platform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(3): 933-950.

[7] 肖忠源, 徐华平, 李春生. 弹载斜视SAR成像的改进波数域算法[J]. 电子与信息学报, 2011, 33(6): 1453-1458.

Xiao Zhong-yuan, Xu Hua-ping, and Li Chun-sheng. A modified wave-number domain algorithm for missile-borne squinted SAR data processing[J]. Journal of Electronics & Information Technology, 2011, 33(6): 1453-1458.

[8] Zhang Shuang-xi, Xing Meng-dao, Xia Xiang-gen, et al.. Focus improvement of high-squint SAR based on azimuth dependence of quadratic range cell migration correction[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(1): 150-154.

[9] Sun Guang-cai, Jiang Xiu-wei, Xing Meng-dao, et al.. Focus improvement of highly squinted data based on azimuth nonlinear scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2308-2322.

[10] 周松, 包敏, 周鹏, 等. 基于方位非线性变标的弹载SAR下降段成像算法[J]. 电子与信息学报, 2011, 33(6): 1420-1426.

Zhou Song, Bao Min, Zhou Peng, et al.. An imaging algorithm for missile-borne SAR with downward movement based on azimuth nonlinear chirp scaling[J]. Journal of Electronics & Information Technology, 2011, 33(6): 1420-1426.

[11] 吴勇, 宋红军, 彭靳. 基于时域去走动的SAR大斜视CS成像算法[J]. 电子与信息学报, 2010, 32(3): 593-598.

Wu Yong, Song Hong-jun, and Peng Jin. Chirp scaling imaging algorithm of SAR in high squint mode based on range walk removal [J]. Journal of Electronics & Information Technology, 2010, 32(3): 593-598.

[12] 肖忠源, 徐华平, 李春生. 基于俯冲模型的频域距离走动校正NLCS-SAR成像算法[J]. 电子与信息学报, 2013, 35(5): 1090-1096.

Xiao Zhong-yuan, Xu Hua-ping, and Li Chun-sheng. NLCSSAR imaging algorithm with range-walk correction in frequency domain based on dive model[J]. Journal of Electronics & Information Technology, 2013, 35(5): 1090-1096.

[13] Wang Yan, Li Jing-wen, Chen Jie, et al.. A parameteradjusting polar format algorithm for extremely high squint SAR imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 640-650.

[14] An Dao-xiang, Huang Xiao-tao, Jin Tian, et al.. Extended nonlinear chirp scaling algorithm for high-Resolution highly squint SAR data focusing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(9): 3595-3609.

[15] Liu Gao-gao, Li Peng, Tang Shi-yang, et al.. Focusing highly squinted data with motion errors based on modified non-linear chirp scaling[J]. IET Radar, Sonar & Navigation, 2013, 7(5): 568-578.

[16] Tang Shi-yang, Zhang Lin-rang, Guo Ping, et al.. An omega-K algorithm for highly squinted missile-borne SAR with constant acceleration[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(9): 1569-1573.

李震宇： 男，1991年生，博士生，研究方向为弹载SAR成像.

梁 毅： 男，1981年生，副教授，博士，研究方向为SAR成像处理、实时成像处理等.

邢孟道： 男，1975年生，教授，博士，研究方向为SAR/ISAR成像、动目标检测等.

保 铮： 男，1927年生，教授，中国科学院院士，研究方向为自适应信号处理、阵列信号处理、雷达成像、目标识别等.

A Frequency Phase Filtering Imaging Algorithm for Highly Squint Missile-borne Synthetic Aperture Radar with Subaperture

Li Zhen-yu Liang Yi Xing Meng-dao Bao Zheng
(National Key Laboratory of Radar Signal Processing, Xidian University, Xi,an 710071, China)

The missile-borne Synthetic Aperture Radar (SAR) usually adopts the highly squint mode and subaperture to satisfy maneuvering and the real-time processing, but the signal of highly squint SAR is coupled greatly between the azimuth and range. This issue can be solved by removing the range walk in the time domain, but costs the limitation of focus depth. Due to the depth of focus and the characteristics of subaperture, a new subaperture imaging algorithm-Frequency Phase Filtering Algorithm (FPFA) is proposed in this paper. Without any approximation of the slant range, the range walk can be done in the time domain and the range curvature removed in the frequency domain. Then, a new high-order equation of phase filtering factor is introduced into the frequency domain in order to correct the azimuth-dependence. Finally, the signal is focused in the Doppler domain by SPECtral ANalysis (SPECAN) technique. Both the simulation results and real data processing validate the effectiveness of the proposed method.

Missile-borne SAR; Subaperture; Highly squint; Frequency Phase Filtering Algorithm (FPFA); SPECtral ANalysis (SPECAN) technique

TN957.52

： A

：1009-5896(2015)04-0953-08

10.11999/JEIT140618

2014-05-12收到，2014-08-14改回

国家自然科学青年基金(61101245)和中央高校基本科研业务费专项资金(K5051302046)资助课题

*通信作者：李震宇 zhenyuli_2012@sina.com