介质目标的太赫兹波近场散射特性计算

程志华谢拥军 马晓东 毛煜茹 毕 博

(北京航空航天大学电子信息工程学院 北京 100191)

介质目标的太赫兹波近场散射特性计算

程志华*谢拥军 马晓东 毛煜茹 毕 博

(北京航空航天大学电子信息工程学院 北京 100191)

该文基于广义的Kirchhoff阻抗边界条件和物理光学法，对太赫兹频段介质体近场散射特性进行了研究，给出了介质体近场散射计算公式。针对在太赫兹频段由于波长较短引起的计算量大幅提升的问题，采用以面元为计算单位、以像素为遮挡判断单位的太赫兹频段介质体近场散射的快速计算方法，该方法在保证计算精度的基础上，大大降低了计算复杂度和时间。计算了圆柱体和鸭嘴形介质体在不同距离下的雷达散射截面，并且分析了电磁场与物体相互作用后，相位项在不同距离、不同频率下对介质体雷达散射截面的影响。

雷达散射截面；图形电磁学；太赫兹；近场

1 引言

太赫兹(THz)波通常是指介于0.1～10.0 THz之间的电磁波，在电磁波谱中太赫兹波处于红外和微波之间。由于太赫兹频段的空间分辨率和时间分辨率频率都很高，与微波和X射线成像相比，太赫兹成像不仅可以显示更精密的图像，还可以获得频域内的相位信息，因此太赫兹成像技术是太赫兹应用的关键技术。太赫兹成像是一个典型的电磁逆散射问题，是通过接收目标散射数据重建描写介质或目标特性的基本函数，同时，由于太赫兹频段频率较高，近场距离范围大幅度提升，成像中散射模型应为近场散射计算模型。因此，太赫兹频段介质目标近场散射特性的研究是十分重要和有意义的。

太赫兹频段目标散射特性研究可分为实验测量、数值计算两种手段。在实验测量上，美国麻省LOWELL大学毫米波实验室利用1.56 THz源在紧缩场中对粗糙面圆柱体的目标散射特性进行了研究[1]。新泽西理工学院物理系对太赫兹频段危险物品的散射成像进行了研究[2]。天津大学太赫兹研究中心搭建了以0.2 THz 返波管振荡器源、热释电探测器、小型自动旋转光学平台等组成的太赫兹波目标散射特性实验测试系统，并对粗糙铜面的散射特性等进行了研究[3]。首都师范大学太赫兹实验室研制了太赫兹数字全息成像系统，该系统可以对太赫兹电磁波的振幅、相位、频率及偏振等全部光学信息的3维空间分布进行精确测量[4]。

在数值计算领域，东南大学毫米波实验室对太赫兹波频段的金属目标体的远场目标特性计算进行了研究，对比分析了多种电磁计算方法，并且独立自主地开发了准确高效的目标特性和电磁兼容仿真分析软件[5]。本课题组对太赫兹频段金属目标的近场散射特性计算进行了研究，并取得了一定成果。介质体近场散射特性的研究较少见报道，远场条件下，目标的散射特性已得到广泛的研究[6−11]，介质目标体计算方法可以分为3类：一是以等效流为基础的方法[12]；二是近似边界条件法(ABC)[13]；三是数值方法，如基于积分方程的矩量法、快速多极子法、体积分方程法等，基于微分方程的有限元法、时域有限差分法等，高频方法有射线追踪法(SBR)、几何光学法(GO)、物理光学法(PO)、几何绕射理论(GTD)等。基于上述方法，近场条件下，目标体RCS的计算思路主要有两种：一种是将物体表面剖分成小面元，用远场RCS计算方法分别计算各小面元的RCS值，然后通过相位叠加得到总的散射场，是从部分到整体的思路[14]。另外一种是以物理光学法为基础，通过散射场积分方程在无远场近似的情况下推导得出的方法，是从整体到部分的思路[15]。在近场区域，不同距离下的近场散射分析更具实际意义，目标体照射区域将随着距离的不同而变化，随之相互遮挡情况也会产生变化，从而导致大量的时间用在相互遮挡的判断上，因此，采用上述的高频方法仍需要耗费极大的内存和极长的计算时间。1993年RIUS等人[16]提出了基于PO的图形电磁学(GRECO)方法，该方法充分利用了计算机硬件的优势，由计算机硬件完成最困难、最费时的遮挡和消影工作，这使得它具有很大的工程应用价值，但是GRECO方法只适用于远场区域的电磁散射计算，并且GRECO方法以提取像素颜色强度获得参数的本质决定其无法适用于太赫兹频段近场的计算。如何把GRECO方法在遮挡判断上的优势应用在太赫兹频段近场散射计算中是十分有意义和价值的。

本文利用基于广义的Kirchhoff的阻抗边界条件对介质体近场RCS计算公式进行了推导。基于PO和GRECO方法，提出一种以面元为计算单位、以像素为遮挡判断单位的太赫兹波介质体近场RCS的快速计算方法。该方法在保证计算精度的基础上，大大降低了遮挡判断的计算复杂度和时间。以圆柱体和鸭嘴形介质体在不同距离下的雷达散射截面的计算为例，验证了本文方法的有效性和准确性。

2 理论分析

2.1 介电性质

德拜方程是讨论一般介质极化弛豫特性的重要关系式，它给出了介电常数和频率的关系，可表示为

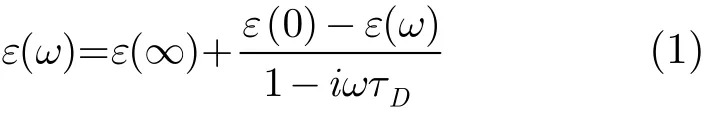
其中ε(0)为静态介电常数，ε(∞)为高频节点常数，τD为弛豫时间，当介质体的弛豫时间的倒数远大于电磁波频率时，由式(1)可知，介质介电常数可近似认为是ε(0)。太赫兹频段，频率在1011～1013Hz 之间，而大部分介质体的弛豫时间大于皮秒级，因此在太赫兹频段，大部分介质体的介电常数将是与介质体弛豫时间、高频介电常数和静态介电常数相关的变量。材料的弛豫时间和介电常数无法通过理论推导求出，需要通过实验获得，目前针对太赫兹频段的物质特性的研究大都通过对吸收系数和折射系数展开，通过折射系数和吸收系数可以求得介质的介电常数。

2.2 近场介质体散射计算理论

由Stratton-Chu积分公式，当散射体内无电磁源时，无远场近似的散射场为

其中Es为目标体散射电场，积分面S为光照区表面，ds为表面单位单元，其单位法向矢量为n, s为散射场方向单位矢量，J为电流密度，E和H分别为总电场和总磁场，Z0为波阻抗，φ=ejkr/r, φ1= ejkr/r2, r为源与面元ds的距离，其单位矢量为r。假设物体表面的曲率半径远大于波长，考虑接收单位的极化方向，由散射场积分方程可得

其中i为入射场方向单位矢量，iH为入射磁场。

由于是球面波入射，因此，

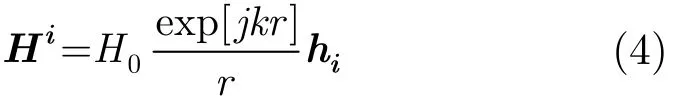
其中hi为入射磁场方向单位矢量，由式(3)，式(4)可得

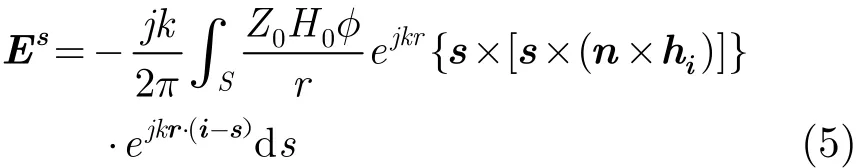
近场雷达散射截面公式可定义为

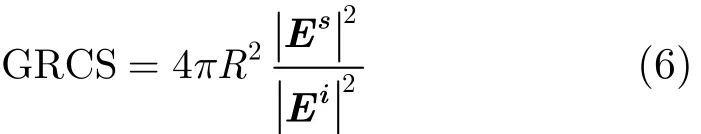
其中R为源点到目标体中心的距离。

利用广义的Kirchhoff的阻抗边界条件，介质体表面电流和磁流可以表示为

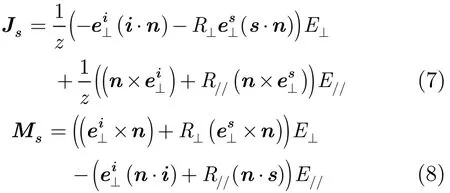
由式(5)，式(6)结合式(7)，式(8)化简后得到介质体近场RCS的计算表达式为

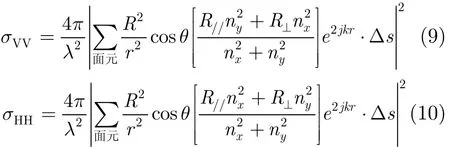
R⊥,R//分别为介质表面在垂直极化和水平极化时的反射系数，对非磁性介质进行考虑，μ1=μ2=μ0，其可表示为

其中ε1, ε2分别为空气和媒质介电系数。

3 太赫兹频段近场散射快速计算方法

由式(9)，式(10)可知，该计算公式是以面元为计算单位。在太赫兹频段，为保证计算结果的准确性，剖分面元将会是千万级的数量，甚至更高，以面元为遮挡判断单位计算量十分巨大，因此，物理光学法在太赫兹频段的RCS计算中工程应用性很低。以像素为计算单位的图形电磁学方法，在判断遮挡上具有很大的优势，但是，图形电磁学中，计算所需参数是以像素为单位通过对光强值的提取来得到的，一般情况下颜色分配模式为RGBA模式，硬件为R, G, B, A成分保留一定数量的位平面。目前显卡支持的最高颜色位数为32位，R, G, B和A各占8位，8 位的R成分可以存储0～255之间的整数[17]。位平面中的0,1,…,255将对应于0/255=0.0, 1/255,…,255/255=1的颜色值，因此，通过光照提取出来的参数值都将是1/255=0.0039的倍数，而太赫兹频段频率范围在0.1～10.0 THz之间，最低频率0.1 THz时，波长为0.003 m，对比通过光照提取的参数值的分辨率(1/255)，可知以像素为计算单位，通过提取像素颜色强度来获得所需参数的方法无法满足太赫兹频段的计算需求。同时，在近场的计算中，由于是球面波照射，照射区域和相位因素不能通过平面波光源和深度缓存得到，因此传统的图形电磁学中提取参数方法和遮挡判断方法在太赫兹目标散射的计算中完全失效。本文通过以面元为计算单位保证太赫兹频段散射特性计算精度，以像素为遮挡判断单位保证遮挡判断的快速性，最终通过建立像素与面元的对应关系从而达到快速计算太赫兹目标近场散射值的目的。由式(9)，式(10)可知，所需计算的参数包括：各面元到光源的距离，各面元法向与入射波夹角的余弦值。

按照目标体实际尺寸，用FEMAP对其进行建模并进行剖分，剖分文件中包括各面元的法相矢量和位置信息。每一个面元的信息包括3个顶点的坐标(x1,y1,z1),(x2,y2,z2),(x3,y3,z3)和面元的法相矢量n，点源的坐标(x,y,z)可以通过光源的位置设置得到。根据坐标和法向可以得到各面元到点源的距离和入射波与面元法向的夹角余弦值。

在近场条件下，照射区域将随距离的变化而变化，随着遮挡情况也会产生变化。通过OPENGL将光源设置为位置性光源，光源位置信息通过模型视图矩阵进行变化，并以视觉坐标的形式存储。光照区域将随光源位置的不同自动进行光照区域判断，结合深度缓存自动进行遮挡处理，从而得到准确的光照区域。利用OPENGL将消隐后的目标图像显现在计算机屏幕上，如图1所示。

图1 随距离变化的光照区域变化

光照区域的面元颜色是以像素为单位进行存储的，无法直接判断面元是否处于光照区域。通过OPENGL工具函数库中的gluUnproject函数将屏幕上光照区像素与剖分体面元一一对应，从而以像素为光照区域判断单位，当像素有颜色时，由对应的面元进行计算。在计算过程中会出现单个像素对应多个面元的情况，在这种情况下通过利用OPENGL的深度缓存判定离剪裁面最近的面元为计算单位，放弃其他面元的计算。为了防止出现单个像素对应多个面元的情况，采用远场散射计算中的分屏显示方法，保证像素对应的实际的尺寸小于或等于面元剖分精度。

以半径0.254 m球体为例，入射频率300 GHz，剖分精度为1/3波长(m)，所需要的分屏数为

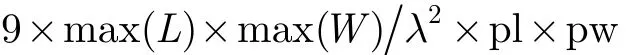
其中max(L), max(W)分别为目标体最大长度和最大宽度；pl, pw分别别为显示区域像素的长度和宽度。该方法的计算量为

射线法是通过判断各剖分面元中点与源点形成的射线与其他面元是否相交，然后保留与源点最近的面元进行计算。DirectX中采用的就是此方法，其具体计算方法是：通过求解三角形面元中两条边的权重u,v，如果u+v≤1则判定射线与该面元存在交点，其计算量为：n(n−1)×[N(u)+M(v)+1]，其中n为面元数，N(u), M(v)分别为u,v的计算量。

表1为同样以半径0.254 m球体为目标体，入射频率为300 GHz，剖分精度为0.0003 m时，采用射线法判断遮挡与本文方法的计算量对比。从表1可以看出，采用本文方法大幅度减少了计算量。

表1 射线法与本文方法遮挡判断的计算量对比

4 计算结果及分析

为验证本文方法的有效性，计算了边长为0.3 m的介质立方体在距离为0.04 m时的近场RCS，入射波长为1 m, εr=4, ur=1，入射方向为与立方体表面法向夹角5°～40°的范围，计算间隔5°。文献[18]中采用矩量法(MOM)对其进行了计算，两者计算结果如图2所示，从中可以看出当角度较小时与文献[18]中计算结果与本文计算结果吻合较好，当角度增大时误差略微增大(由棱边引起)，最大误差小于1 dB，因此验证了本文方法的正确性和有效性。

图2 介质立方体近场RCS本文计算结果与文献计算结果对比

以介质体为含碳纳米结构的高分子复合材料为例[19]，分别计算了圆柱体和同比尺寸缩小后的鸭嘴型散射体，计算频率为100 GHz, 200 GHz和300 GHz，其介电常数如表2所示。

表2 含碳纳米结构的高分子复合材料介电常数表

(1)介质圆柱体计算距离为10～200 m，剖分精度为0.0005 m，正Z轴入射，垂直极化，模型如图3所示，计算结果如图4所示。

图3 圆柱介质体模型

从图4可以看出当目标体与源距离较近时，同一距离下，不同频率的近场RCS值并没有像远场RCS一样随频率的增大而增大，随着距离的增加，频率与近场RCS值逐渐成单调趋势。图5为固定介电常数为12.45，圆柱介质体在频率1～200 GHz，距离分别为10 m, 50 m和200 m时的近场RCS值。可以看出，当距离较近时，近场RCS值随频率的增大波动较强；当距离较远时，近场RCS值随频率的增加波动降低。由式(16)，式(17)可知，当距离不变、频率发生变化时，只有系数项4π/λ2与相位项e2jkr(其中k=2π/λ)发生变化，其中系数项与频率成单调正比趋势，结合图5中的计算结果，可以认为在近场散射计算中，当距离越近时，相位项对近场散射值的影响越大；随着距离的增加，相位项对近场散射值的影响越来越小，到达远场条件时，散射值与频率成正比，本文计算结果与远场计算结果吻合。

(2)同比尺寸缩小后的鸭嘴型散射体，计算距离为1～50 m，正Z轴入射，水平极化，剖分精度0.0005 m，模型如图6所示，计算结果如图7所示。

图4 圆柱介质体10～200 m近场RCS

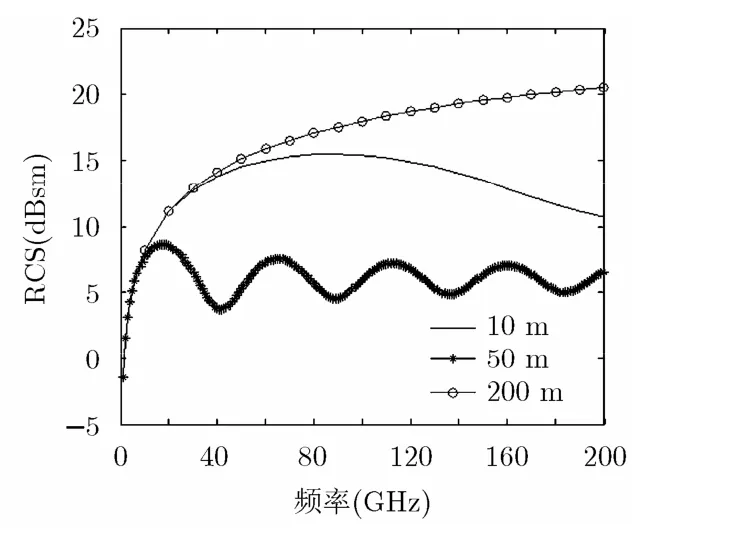
图5 1～200 GHz固定距离圆柱介质体近场RCS

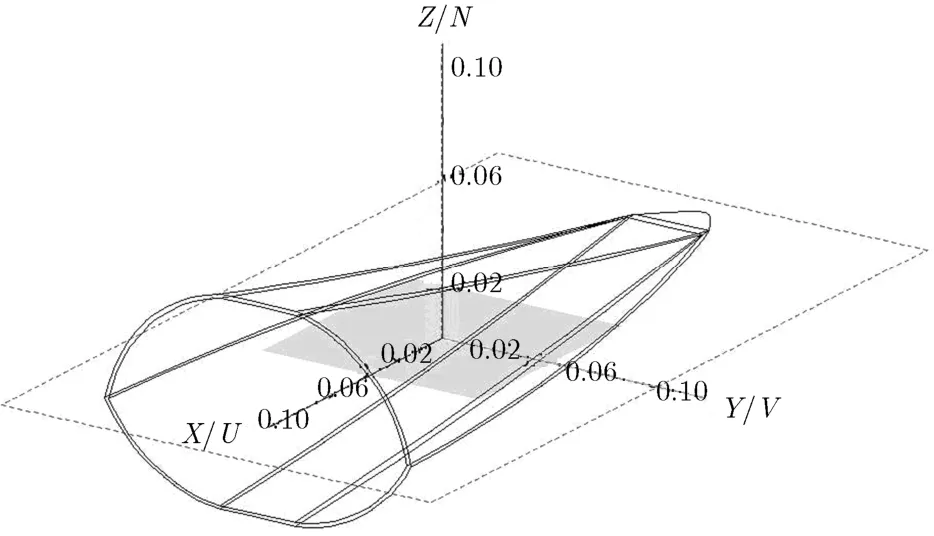
图6 鸭嘴型天线罩介质体模型

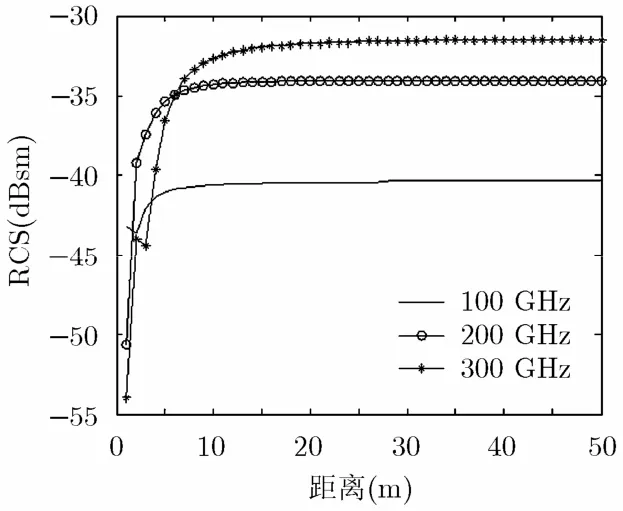
图7 鸭嘴型散射体不同频率近场RCS

从图7中同样可以看出，当距离越远时相位项对近场RCS值的影响越小，在近距离一定范围内，近场RCS值并不随频率增加而增大，当到达远场条件时与远场计算结果吻合。

5 结论

本文研究了太赫兹频段介质目标体的近场散射特性，基于广义的Kirchhoff阻抗边界条件和物理光学法对介质体近场散射计算公式进行了推导，采用以面元为计算单位，以像素为遮挡判断单位的太赫兹近场散射的快速计算方法。该方法利用OPENGL引入点光源和深度缓存结合的光照区域判断方法，由计算机硬件自动完成耗时的遮挡和消隐以及建立面元与像素之间的对应关系，从而快速准确地计算了太赫兹频段介质目标的近场雷达散射截面，并且分析了电磁场与物体相互作用后，相位项在不同距离、不同频率下对介质体雷达散射截面的影响。

[1] Danylov A A, Goyette T M, Waldman J, et al.. Terahertz inverse synthetic aperture radar (ISAR) imaging with a quantum cascade laser transmitter[J]. Optics Express, 2010, 18(15): 16264-16272.

[2] Federici F, Schulkin B, Huang F, et al.. THz imaging and sensing for security applications-explosives, weapons and drugs[J]. Semiconductor Science and Technology, 2005, 20(2): S266-S280.

[3] 杨洋, 姚建铨, 张镜水, 等. 粗糙铜表面对低频太赫兹波的散射实验[J]. 红外与毫米波学报, 2013, 32(1): 36-39.

Yang Yang, Yao Jian-quan, Zhang Jing-shui, et al.. Terahertz scattering on rough copper surface[J]. Journal of Infrared and Millimeter Waves, 2013, 32(1): 36-39.

[4] 郑显华, 王新柯, 孙文峰, 等. 太赫兹数字全息术的研发与应用[J]. 中国激光, 2014, 41(2): 1-10.

Zheng Xian-hua, Wang Xin-ke, Sun Wen-feng, et al.. Developments and applications of the terahertz digital holography[J]. Chinese Journal of Lasers, 2014, 41(2): 1-10.

[5] Li Zhuo, Cui Tie-jun, Zhong Xing-jian, et al.. Electromagnetic scattering characteristics of PEC targets in the terahertz regime[J]. IEEE Antennas and Propagation Magazine, 2009, 51(1): 39-50.

[6] Solomon R C, Leong H, and Antar Y M. Forward scattering effects in RCS of complex targets in the 3-20 MHz high frequency range[C]. Antennas and Propagation Society International Symposium, Boston, 2008: 1-4.

[7] 李晓峰, 谢拥军, 杨锐. 半空间电大导体目标散射的高频分析方法[J]. 电子与信息学报, 2009, 31(5): 1268-1270.

Li Xiao-feng, Xie Yong-jun, and Yang Rui. High-frequency analysis on scattering from conductive targets with electrically large size in half space[J]. Journal of Electronics & Information Technology, 2009, 31(5): 1268-1270.

[8] Gillion E, Rochefort E, and Claverie J. Improvement of RCS estimation of large targets by using near-field approach[C]. IEEE Radar Conference (RADAR), Ottawa, ON, Canada, 2013: 1-5.

[9] Altin N and Yazgan E. RCS prediction using fast ray tracing in Plücker coordinates[C]. 2013 7th European Conference on Antennas and Propagation (EuCAP), Gothenburg, 2013: 284-288.

[10] Lipuma D, Méric S, and Gillard R. RCS enhancement of flattened dihedral corner reflector using reflect array approach[J]. Electronics Letters, 2013, 49(2): 152-154.

[11] Li Xiao-feng, Xie Yong-jun, and Yang Rui. High-frequency method for scattering from coated targets with electrically large size in half space[J]. IEEE Transactions on Antennas and Propagation, 2009, 57(2): 181-186.

[12] Huddleston P L, Medgyesi-Mitschang L N, and Putnam J M. Combined field integral equation formulation for scattering by dielectrically coated conducting bodies[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(4): 510-520.

[13] Senior T B A and Volakis J L. Generalized impedance boundary condition in scattering[J]. Proceedings of the IEEE, 1991, 79(10): 1413-1420.

[14] Li Jing and Li Xiang-jun. An efficient algorithm for near field RCS of electrically large dynamic targets[C]. International Conference on Information Science and Technology, Nanjing, 2011: 413-415.

[15] Pouliguen P, Damiens J F, et al.. RCS computation in near field[C]. Proceedings of the International Conference Day on Diffraction, Petersburg, 2006: 252-265.

[16] Rius J M, Ferrando M, and Jofre L. High frequency RCS of complex radar targets in real time[J]. IEEE Transactions on Antennas and Propagation, 1993, 41(9): 1308-1319.

[17] Shreniner D. The Khronos OpenGL ARB Working Group.

李军, 徐波, 等译. OPENGL编程指南[M]. 第7版, 北京: 机械工业出版社, 2010: 118-119.

[18] 贺昌辉. 矩量法分析目标的近场电磁散射[D]. [硕士论文], 华中师范大学, 2006.

He Chang-hui. The analysis of near-field EM scattering from targets by moment methods[D]. [Master dissertation], Central China Normal University, 2006.

[19] Zhuravleva V A, Suslyaeva V I, and Dunaevskiia G E. Complex permittivity of polymer composites containing carbon nanostructures in frequency range 0.17-1.1[C]. International Conference on THz Infrared, Millimeter and Terahertz Waves (IRMMW-THz), Wollongong, NSW, 2012: 1-2.

程志华： 男，1982年生，博士生，研究方向为计算电磁学、太赫兹目标特性、天线工程、电磁兼容等.

谢拥军： 男，1968年生，教授，研究方向为计算微波与计算电磁学、微波通信、天线工程、电磁兼容等.

毛煜茹： 女，1984年生，博士生，研究方向为计算电磁学、天线工程、电磁兼容等.

马晓东： 男， 1989年生，硕士生，研究方向为目标特性、天线工程、电磁兼容等.

毕 博： 男，1993年生，硕士生，研究方向为目标特性等.

Near-field Electromagnetic Scattering Characteristics of Dielectric Targets in the Terahertz Regime

Cheng Zhi-hua Xie Yong-jun Ma Xiao-dong Mao Yu-ru Bi Bo
(School of Electronic and Information Engineering, Beihang University, Beijing 100191, China)

The near-field scattering characteristics of dielectric targets are studied in the terahertz band based on the generalized Kirchhoff impedance boundary conditions and the physical optics method. The formula of the near field scattering for dielectric targets is deduced. In the light of the increase in calculation amount caused by the shorter wavelength, a fast computational method using surface element as the calculating unit and pixel as occlusion judgment unit is proposed for the near field scattering computation in terahertz band. The method ensures the calculation accuracy and reduces greatly the computational complexity and the time consumption of occlusion judging. The calculation of the near-field Radar Cross Section (RCS) produced by a dielectric cylinder and a duck mouth scatterer is performed in terahertz band. Meanwhile, the effect of the phase on the near field RCS in different distances and frequency is analyzed.

Radar Cross Section (RCS); GRaphical-Electromagnetic COmputing (GRECO); Terahertz; Near field

TN011

： A

：1009-5896(2015)04-1002-06

10.11999/JEIT140807

2014-06-20收到，2014-08-15改回

*通信作者：程志华 asakaka1982@163.com