虚拟社区知识共享困局及应对——基于无限重复博弈

(兰州财经大学工商管理学院，甘肃 兰州730000)

据CNNIC发布的《第34次中国互联网发展状况统计报告》显示，截至2014年6月中国网民规模达到6.32亿，其中手机网民达5.27亿，以微博为代表的网络虚拟社区用户，增长到2.78亿，成为用户增长最快的互联网应用模式。但是，没有社区知识共享活动，任何虚拟社区就会无法生存［1］。庞大的网络用户使网络虚拟社区逐渐成为更为强大的信息交互平台，社区中的信息和知识可以直接从一个社区成员传递到任意一个社区成员，而无需采用传统的交流方式。此时虚拟社区可以被理解为一个基于计算机技术的知识型社区的形式［2］。社区成员不再满足于传统的信息交流与沟通的需求，在社区获取知识并通过互动交流创造出新的知识是社区成员的最终目标。网络虚拟社区是一个很有效的知识共享平台，但并不具备天然的知识共享属性，因为社区成员之间的关系并非简单的合作、共赢关系，在知识共享具有成本的情况下，社区成员也会存在竞争。社区成员之间的合作、竞争、同化、冲突、适应会影响社区的知识共享水平，从博弈论的视角厘清虚拟社区成员间的关系和行为，进而解读虚拟社区的知识共享困局具有一定的现实意义。

1 文献回顾

Rheingole(1993) 在《虚拟社区》一书中，将虚拟社区定义为“由计算机网络彼此沟通的、有某种程度的认知、分享某种程度的知识和信息的人们形成的团体”［3］。虚拟社区的团体属性使得关于虚拟社区知识共享问题的研究与知识管理中组织内部或组织间的知识共享研究密切相连，相关研究缺乏网络环境下的现实考量。随着互联网的飞速发展，网络虚拟社区的知识共享问题研究才逐渐从知识管理的框架中脱离出来。关于虚拟社区知识共享困局的研究，很多学者从不同的角度提出了不同的观点。Fnholt＆Sproull(1990) 认为，虚拟社区知识共享存在两个难点:一是知识的爆炸;二是知识过少［4］。“知识量”并非导致虚拟社区知识共享困局的“悖论”，一方面，海量知识会增加社区成员甄别知识的成本;另一方面，知识量过少难以使虚拟社区产生足够的正外部性。在网络环境已经发生较大改变的今天，这个观点仍有一定价值。Valtersson(1996) 则认为大多数虚拟社区或多或少地设置了一些障碍，如交纳会员费和注册会员，由此影响了虚拟社区获取知识的便利性［5］。实践证明“会员制”对于虚拟社区知识共享具有重要意义，通过缴纳会费和注册会员形成的“会员制”，一方面提高了虚拟社区知识共享的门槛;另一方面改变了虚拟社区知识共享博弈的有界性，使社区成员间的知识共享行为不受有限次策略的影响，而长期进行下去。Alexander(2003) 认为决定虚拟社区知识共享成败的关键因素，取决于社区成员在知识产生和共享中的动机和积极性［6］。李雪松等(2008) 将一个不包含噪声的不完全信息博弈模型引入到虚拟社区知识共享问题中，发现不共享社区成员群体过大和信息不对称，是导致虚拟社区知识共享效果不佳的主要原因［7］。

以上文献从不同的角度分析了阻碍虚拟社区知识共享的因素，具有一定的科学性。但是，现有的研究似乎都忽视了社区成员间关系和社区环境对虚拟社区知识共享的影响。虚拟社区知识共享的过程就是社区成员博弈的过程，通过分析从静态博弈到动态博弈的转化影响因素以及博弈模型在不同条件下达到的均衡状态，可以确定导致虚拟社区知识共享困局的原因。

2 虚拟社区知识共享困局的产生:不完全信息条件下虚拟社区知识共享的囚徒困境

在非“会员制”的专业虚拟社区中，社区知识是开放的，专业搜索引擎网站的出现使社区成员倾向于通过网络搜索获取知识，从而导致社区成员构成极其不稳定，社区成员具有不完全信息。为了便于分析，提出不完全信息条件下虚拟社区知识共享博弈模型假设:

假设1:虚拟社区知识共享博弈中有两个参与人，参与人1和参与人2，参与人是理性的，知识共享的目的是实现个人期望效益最大化。

假设2:参与人1和参与人2具有相等的知识量，记为q。参与者为了共享知识需要耗费一定的时间、精力等，付出的贡献成本为c。

假设3:存在参与者掌握同一种知识的可能性，如果参与者共同掌握某种知识，任何一方共享知识也不会使知识总量增加，我们把这用知识重叠性ko(Knowleged overlap) 表示，且0＜ko＜1。知识重叠性反映了个体拥有知识的独特程度和冗余程度［8］。参与双方全部共享知识的情况下，知识量的增加必须要减去参与双方共有的知识量。

假设4:专业型虚拟社区共享的知识主要为显性知识，社区成员可以很容易地获取，且完全具备吸收这些显性知识的能力。

两个参与者均有3个策略可供选择，即“发帖”P(Posting) 、“评论”C(Commonting) 和“浏览”B(Browsing) 。“发帖”和“评论”表示参与者愿意进行知识共享，只是共享的程度不同，“发帖”意味着参与者愿意全面共享知识，而“评论”仅仅是部分共享知识，“浏览”则表示不共享知识。参与者选择浏览策略时，可以选择共享知识量的任何比例，记为r，大量的实证研究表明:r受到多种因素的影响，如信任、自我效能、结果预期等［9－10］。

笔者将博弈参与者选择“发帖”策略的概率定为xp，选择“评论”策略的概率为xc，选择“浏览”策略的概率为xb，且xp+xc+xb=1。δ为获取新知识后转化为收益的贴现因子。博弈双方知识共享的收益矩阵如图1所示。

图1 虚拟社区知识共享博弈收益矩阵

该收益矩阵共有9种不同的策略组合:

(1) 在(P1，P2) 策略组合中，博弈双方都选择发帖策略，参与人1获得参与人2共享的净知识量q－ko，这些新获取的知识能给他带来δ(q－ko) 的收益，参与人1发帖的成本为c，故参与人1和参与人2获取的收益均为xp［δ(q－ko) －c］。

(2) 在(P1，C2) 策略组合中，参与人1选择发帖策略，参与人2选择评论策略，参与人1获得参与人2共享的净知识量r(q－ko) ，获得的净收益为xc［rδ(q－ko) －c) ］;参与人2获得的净知识量为(q－ko) ，付出的成本为rc，故参与人2获得的净收益为xp［δ(q－ko) －rc］。同理，在(C1，P2) 策略组合中，参与人1的净收益为xp［δ(q－ko) －rc］，参与人2的净收益为xc［rδ(q－ko) －c) ］。

(3) 在(P1，B2) 策略组合中，参与人1选择发帖策略，参与人2选择浏览策略，参与人1没有获得任何新知识，其净收益为－xb c;参与人2获得的净知识量为(q－ko) ，净收益为xpδ(q－ko) 。同理，在(B1，P2) 策略组合中，参与人1的净收益为xpδ(q－ko) ，参与人2的净收益为－xb c。

(4) 在(C1，B2) 策略组合中，参与人1选择评论策略，参与人2选择浏览策略，参与人1没有获得任何新知识，其净收益为－xb c;参与人2获得的净知识量为r(q－ko) ，净收益为xc rδ(q－ko) 。同理，在(B1，C2) 策略组合中，参与人1的净收益为xc rδ(q－ko) ，参与人2的净收益为－xb c。

(5) 在(C1，C2) 策略组合中，参与人1和参与人2均共享一部分知识，参与人1获得的新知识量为r(q－ko) ，付出的成本为rc，净收益为xc［rδ(q－ko) －rc) ］，参与人2的净收益为xc［rδ(q－ko) －rc) ］。在(B1，B2) 策略组合中，参与人1和参与人2都不共享知识，不获取任何知识和收益。

在不完全信息条件下，博弈双方都试图获得最大期望收益xpδ(q－ko) ，最终形成(B1，B2) 的策略组合，导致虚拟社区知识共享陷入“囚徒困境”。由此可见，不完全信息会导致虚拟社区知识共享困局的产生。

3 虚拟社区知识共享困局的消除:合作规则下虚拟社区知识共享无限重复博弈

社区成员往往不会也不能一次性共享所有知识，分享知识的过程存在阶段性，如果改变虚拟社区知识共享博弈信息的完备性，变“不完全信息”为“完全信息”，则虚拟社区知识共享博弈是一个多阶段可观察行动的重复博弈。

用一个行动序列{a0，…，aT}表示社区成员共享知识的过程，在此行动序列中，社区成员共享全部知识，且存在知识量为零的行动。在这里，假设每期收益只依赖当期行动，参与人1在第t期的收益记为g1(at) =x(at)r(at) ［δ(q－ko) －c］。为了使不同期的收益之间具有可比性，笔者用同样的单位对每期收益进行标准化表示，因此，一个行动序列{a0，…，aT}的标准化收益是:

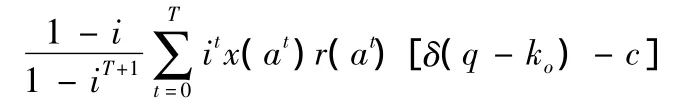
其中i为不同期收益贴现到当期的贴现值。标准化只是改变了权重，因而标准化形式和现值形式都代表了同样的偏好。通过把所有收益用每期平均收益来度量，标准化的形式更容易揭示出当贴现值和期界发生变化时而产生的变化。

3.1 如果博弈只进行1次

“共享”是绝对的劣策略，惟一的均衡是两个参与人都选择不共享知识，即“浏览”策略。

3.2 如果博弈只重复有限次

子博弈完美就要求两个参与人在最后一期博弈时都选择“浏览”策略，根据逆向递归法［11］，则惟一的子博弈完美均衡就是两个参与人在每一阶段都选择“浏览”策略，不共享任何知识。

3.3 如果博弈进行无限多次

当有一个参与人选择不共享，在以后的博弈中，博弈双方都不会共享知识，“浏览”策略就会一直持续下去。当参与人开始时都选择共享，“共享”策略就会一直持续下去，成为无限重复博弈的平衡点，并同时实现双方的合作。因为根据“大众定理” (Folk Theorem) ，在无限次重复博弈中，如果参与个体有足够的耐心，那么，任何满足个人理性的可行的支付向量都可以通过一个特定的子博弈精炼均衡得到，即重复博弈战略均衡支付与一次性博弈中可行的个体理性支付是相一致的［12］。根据大众定理，有无穷多种行为规则可以支持合作行为。在虚拟社区知识共享无限重复博弈中，引入激励机制及提升社区成员所能提供的知识总量是支持社区成员合作行为的有效规则。

囚徒困境重复博弈表明了重复博弈扩大均衡结果集合，此外它还显示了同样的博弈在有限界和无限界中其均衡的集合是截然不同的，特别是，在时期界限变为无限大时可能会出现新的均衡。根据Shaked and Sutton(1984)［13］提出的方法，利用博弈的平稳性得到每个参与人收益的上界和下界，然后设法证明上界和下界相等，可以确定虚拟社区知识共享无限重复博弈将存在惟一的均衡。所以，使虚拟社区知识共享博弈达到纳什均衡的措施是改变博弈的条件和类型，使其成为无限重复博弈，同时引入支持合作的行为规则，达到参与人都共享知识的均衡状态。

4 研究结果及讨论

虚拟社区知识共享受信息的完备性、博弈的界限、参与人的初始策略的影响。不完全信息条件下，虚拟社区知识共享博弈陷入囚徒困境，导致虚拟社区知识共享困局的产生。在完全信息条件下，博弈的界限和参与人的初始策略也将影响博弈的均衡，博弈的有界性和参与人初始策略选择“不共享”都会导致虚拟社区知识共享陷入困局。引入激励机制及提升社区成员所能提供的知识总量可以支持博弈双方的合作行为，使 (共享，共享) 成为无限重复博弈的均衡点。

可以从以下几个方面应对虚拟社区知识共享困局，提升社区知识共享水平:

4.1 合理设置社区门槛

进入社区的门槛过高或过低都会对社区知识共享产生不利影响，进入社区的门槛过高会减少社区成员而降低社区知识总量，进入社区的门槛过低会使知识共享博弈的无界性受损，使成员间知识共享产生单次博弈的投机行为。只有合理设置进入社区的门槛，如采取“会员制”和通过知识共享获取进入社区的权限等方式，才可以使虚拟社区知识共享博弈成为一个无限重复博弈，而达到纳什均衡。

4.2 构建社区知识共享激励系统

强化理论认为人的行为是刺激的函数，如果刺激对他有利，这种行为就会重复出现。可以通过权限激励和虚拟物质激励构建虚拟社区知识共享激励系统，对知识共享者给予访问权限及虚拟物质奖励方面的激励，提高知识共享的积极性。激励策略往往可以增加社区知识共享者的收益，使知识共享成为社区成员一种习惯性地社区行为，如在社区习惯性地分享知识和发表评论。

4.3 培养“意见领袖”

“意见领袖”在网络虚拟社区知识共享中起着中介和模范作用，他在给社区成员施加影响的同时，也会引导社区成员共享知识，发起讨论创造出新的知识。在专业虚拟社区中，“意见领袖”的专业知识和“利他主义”是其权威的保障，社区应当对“意见领袖”进行刻意的引导和培训，鼓励社区成员间的知识共享，营造信任共享的社区文化。

［1］Bulter.B..Membership Size，Community Activity，and Custain Ability:A Resource－based Model of Online Social Structures［J］.Information Systems Research，2001，(4) :346－362.

［2］Azjen.I..The Theory of Planned Behavior［M］.New York:Organizational Behavior and Human Decision Processes，2001:52.

［3］Howard R.The Virtual Community:Homesteading on the Electronic Frontier［M］.MIT:Addison Wesley，1993.

［4］Finholt.T..Electronic groups at work organization Science on Sproull［J］.1990，(1) :41 －64.

［5］Va1tersson.M..Virtual Communities［M］.Department of Informatics Umea University，Sweden，1996:233.

［6］Alexander Ardichvili，Vanghn Page，Tim Wentling.Motivation and Barriers to Participation in Virtual Knowledge－sharing Communities of Practice［J］.Journal of Knowledge Management，2003，(7) :64－77.

［7］李雪松，司有和，谭红成.基于网络外部性的虚拟社区知识共享模型分析［J］.科技管理研究，2008，(4) :250－252.

［8］赵君，廖建桥.团队成员知识共享的进化博弈分析［J］.情报杂志，2009，(9) :122－126.

［9］Shu－Mei Tseng.The Effects of Information Technology on Knowledge Management Systems［J］.Expert Systems with Application，2008，(35) :150－160.

［10］李志宏，等.济虚拟社区成员知识共享意愿影响因素的实证研究［J］.图书情报工作，2009，(6) :53－56.

［11］(美) 朱·非登博格，让·梯若尔博弈论［M］.黄涛，等译.北京:中国人民大学出版社，2010:148－149.

［12］朱艳丽，杨定华.奥曼及其无限重复博弈理论——2005年诺贝尔经济学奖述评［J］.云南财贸大学学报，2006， (6) :12－13.

［13］Shaked.A，J.Sutton.Involuntary unemployment as a perfect equilibrium in a bargaining game［J］.Economica，1984，(52) :1351－1364.