三电平逆变器SHEPWM的一种空间电压矢量合成算法

周熙炜，熊永荣，赵洋，张奕城，侯庆华

（1.国家山区公路工程技术研究中心，重庆400056；2.长安大学电子与控制工程学院，陕西西安710064）

1 引言

优化的PWM脉宽调制技术具有改善逆变器的输出波形，降低开关损耗、优化算法求解、加快调节速度，提高系统的动态、稳态性能等作用。

对于三电平逆变器而言，常用的是SVPWM技术。文献［1］使用的优化SVPWM 技术可进一步提高电压利用率和加快计算实时性。但是，较高开关频率的SVPWM 调制带来较大的开关损耗。与SVPWM 技术相比，特定谐波消去SHEPWM 技术具有开关频率低、波形质量高、输出滤波器尺寸小、易于设计等显著优点，既可以满足波形质量，又有助于降低开关损耗并提高电压利用率。而这一技术中的开关角的在线实时求解问题制约了其使用，其非线性超越方程组的求解与开关角的个数有关。SHEPWM 产生了各种优化方法，典型的以开关角方程组的求解方法不同，有：同伦算法、牛顿下山法［2］、遗传算法、混沌蚁群算法和蜂群算法［3］等。在求解中，方程组初值的选取和多重解的优化也有很多研究。此外，还有一类方法基于规则采样研究了SVPWM 与SHEPWM 之间的内在联系［4］，提出SHEPWM 调制表现为一种脉冲状态由基本SV矢量合成的矢量序列特殊解。

本文介绍了一种三电平逆变器SHEPWM调制的新算法，该算法的开关角可通过基本空间电压SV 矢量的运算而直接合成，并具有同样的消谐效果。

2 三电平SHEPWM的消谐特性

图1a所示为SHEPWM调制的三电平逆变器单相输出电压波形。可以看出，这一波形有1/4周期对称性，其中，以N表示1/4基波周期内的开关角数，E 为直流母线电压。图1b 为N=10 时逆变器的三相开关角的切换波形。

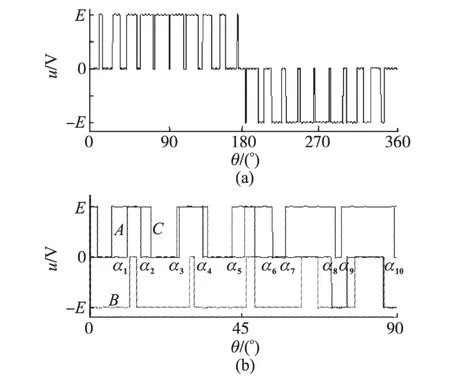
图1 三电平逆变器SHEPWM相电压及开关角Fig.1 The phase voltage and its switching angle of three-level inverter SHEPWM

可对相电压函数进行傅里叶分析：

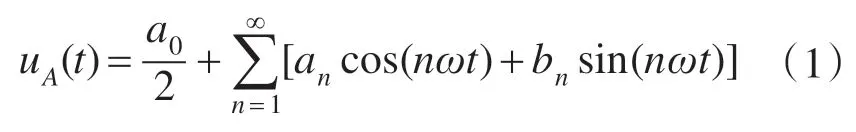
其中

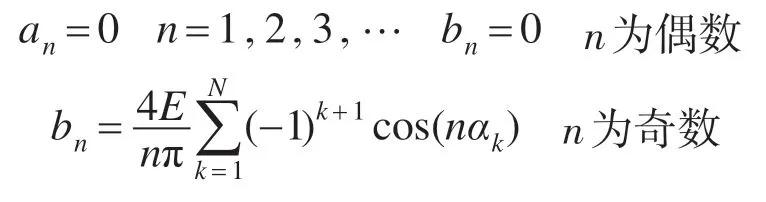
并且，有：

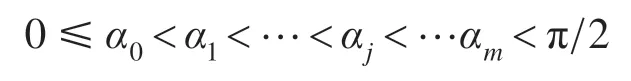
为了消除k次谐波，可使其对应的系数bn=0。N 个开关角可构成N 个独立方程，分别对应N 个谐波的幅值。计算开关角度，并发出相应的SHEPWM 指令波，即可消除掉逆变器的N-1 个非3的整数倍奇次谐波。

3 三电平SHEPWM 的电压矢量合成算法

由于三电平矢量六边形可以分解成两电平小六边形，找到修正后的空间参考电压矢量，三电平可以像两电平逆变器一样确定开关序列和SV 矢量的作用时间。而两电平的SHEPWM 调制可以由基本SV 矢量组成的矢量序列实现［4］。因此，在三电平分解的每一个两电平小六边形中，按照三电平SHEPWM的消谐要求，根据空间电压矢量的工作扇区，选取三电平SHEPWM 所需的基本SV矢量，推导基本SV矢量的作用时间并进行状态切换，合成桥臂开关的SHEPWM 指令并依次发出，即可生成三电平SHEPWM。

3.1 三电平空间矢量的分解

三电平逆变器各桥臂的开关状态组合产生的输出电压状态有3 个：Udc/2，0，-Udc/2，可分别用状态值1，0，-1 表示。三电平的空间电压矢量六边形及其分解图参见图2。

图2 三电平逆变器的空间矢量六边形分解及工作扇区Fig.2 Space vector hexagon decomposition and its work sectors of three-level inverter

对于三电平而言，两电平的六边形的原点都位于三电平逆变器内部六边形的顶点上。以小六边形①为例，三电平的参考矢量V*在开关周期T 内可由3 个与之相邻的矢量V1，V2，合成：

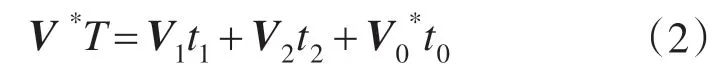
因此，三电平的参考电压矢量V*可以由所对应的两电平中的参考电压矢量V*1来生成，三电平可以像两电平逆变器一样确定开关序列和电压矢量的作用时间。

3.2 SHEPWM的电压矢量合成

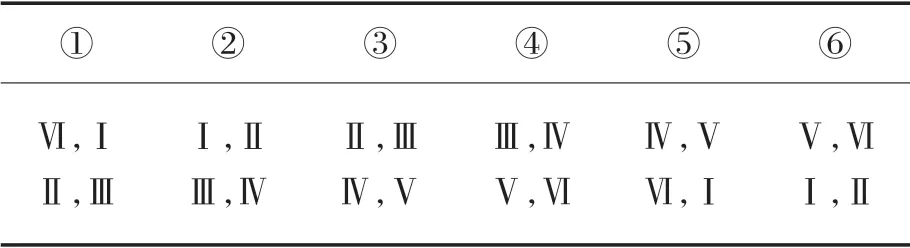
表1 工作扇区分配表Tab.1 Work sector allocation table

表2 SHEPWM的基本矢量切换状态表Ⅰ（M＜1）Tab.2 The basic vector switching state tableⅠof SHEPWM

表3 SHEPWM的基本矢量切换状态表Ⅱ（1≤M≤1.15）Tab.3 The basic vector switching state tableⅡof SHEPWM

表2、表3 中，SA为三相桥臂状态值之和为0的基本电压矢量，SB为状态值之和非0 的基本电压矢量为每个小六边形的零矢量。而零矢量的作用是过渡相邻基本矢量的切换，零矢量的选择应使三相电压状态单阶梯变化且每次只切换一个桥臂。

3.3 SHEPWM的基本电压矢量作用时间

在两电平小六边形中，三电平在对应扇区里的参考电压矢量需要进行偏置修正。修正后的每相参考电压矢量参见表4。

表4 参考电压矢量的修正Tab.4 Correction of the reference voltage vector

每个小六边形中，三电平SHEPWM 的基本电压矢量SA，SB与零矢量的作用时间以k的奇偶不同有：

1）k=奇数时，

而k=N时，

2）k=偶数时，

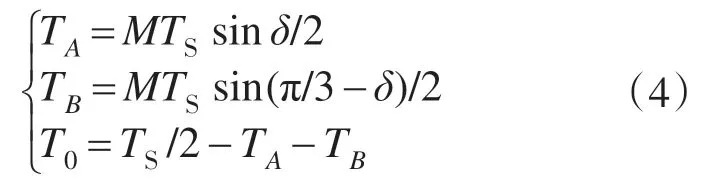
而k=2时，

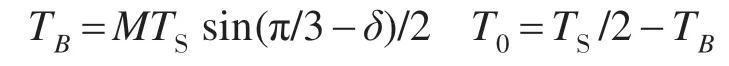
式中：M 为调制度，M=U*/(Ud/2)，U*为参考电压矢量的幅值（实际上是期望输出相电压的基波峰值），Ud为直流母线电压；δ为两电平小六边形中空间电压矢量V*1与基本电压矢量V4的夹角。

3.4 半实物仿真及实现

三电平SHEPWM的电压矢量合成算法研究可以用在Matlab 模型的基础上，用dSPACE 的硬件在回路的半实物仿真来完成，其系统结构如图3所示。

整个系统由dSPACE 软硬件子系统、硬件驱动/保护和功率主电路3 大部分构成。首先建立SV-SHEPWM 算法的Simulink 仿真模型，然后由dSPACE内部实现DSP控制器的代码生成/下载，用DS4002 与仿真模型的接口模块来输出PWM指令信号。

算法的Simulink仿真模型参见图4。系统仿真前需先根据变压变频策略（如VVVF控制），得到参考电压矢量V*、调制度M、谐波次数N。根据空间电压矢量的工作扇区，选取三电平SHEPWM所需的基本SV矢量，推导基本SV矢量的作用时间并进行状态切换，合成桥臂开关的SHEPWM指令并依次发出。

图3 半实物实验系统结构图Fig.3 Hardware-in-the-loop experiment system structure

图4 基于空间电压矢量的SHEPWM单相仿真框图Fig.4 The one-phase SHEPWM simulation block diagram

三电平逆变器直流侧电压为500 V，频率为50 Hz、调制系数为1.15，选定1/4基波周期内的开关角数N=10 时，三电平逆变器的电压矢量合成SHEPWM 算法的输出相电压实验波形如图5 所示；图6是输出线电压波形和中点电位的波形；图7是线电压的FFT分析。

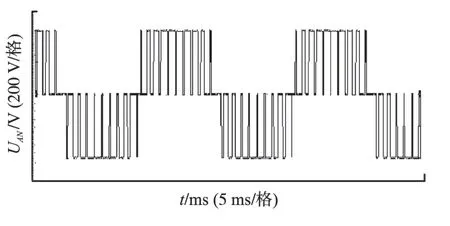
图5 三电平逆变器输出相电压Fig.5 The output phase voltage of three-level inverter

图6 输出线电压及中点电位Fig.6 The output line voltage and neutral voltage

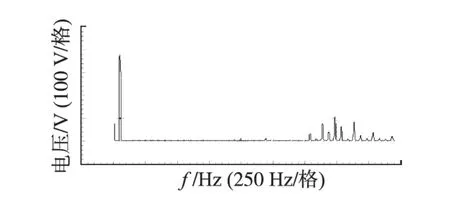
图7 线电压FFT分析Fig.7 The FFT analysis of line voltage

4 结论

三电平逆变器的SHEPWM技术的开关角非线性超越方程组的求解是其应用发展的瓶颈问题，而基于空间电压矢量合成的SHEPWM 算法有助于解决这一问题。但若考虑多重解的影响、逆变器的中点电位、运算实时性及动态性能，这一方法仍需更多的研究。

［1］Vafakhah Behzad. A New Space-vector PWM with Optimal Switching Selection for Multilevel Coupled Inductor inverters［J］. IEEE Trans. on Indus. Elect.，2010，57（7）：2354-2364.

［2］陈金平，贺昱曜，巨永锋，等.基于牛顿下山法的三电平逆变器SHEPWM求解方法［J］.电力电子技术，2013，47（9）：8-10.

［3］Ayoub Kavousi.Application of the Bee Algorithm for Selective Harmonic Elimination Strategy in Multilevel Inverters［J］.IEEE Trans.on Power Elect.，2012，27（4）：1689-1696.

［4］Sidney R Bowes. Optimal Regular-sampled PWM Inverter Control Techniques［J］. IEEE Trans. on Indus. Elect.，2007，54（3）：1547-1559.

［5］Grahame Holmes D，Thomas A Lipo.电力电子变换器PWM技术原理与实践［M］.周克亮，译.北京：人民邮电出版社，2010.

［6］Damoun Ahmadi，Zou Ke，Li Cong，et al. A Universal Selective Harmonic Elimination Method for High-power Inverters［J］. IEEE Transactions on Industrial Electronics，2011，26（10）：2743-2752.

［7］Ayoub Kavousi，Behrooz Vahidi. Application of the Bee Algorithm for Selective Harmonic Elimination Strategy in Multilevel Inverters［J］. IEEE Transactions on Power Electronics，April 2012，27（4）：1689-1696.