基于拉普拉斯分值特征选择的运动捕获数据关键帧提取*
2015-07-10洪小娇彭淑娟
洪小娇,彭淑娟,柳 欣
(华侨大学计算机科学与技术学院,福建 厦门 361021)
1 引言
随着运动捕获技术的快速发展,大量真实的人体运动数据广泛应用于计算机游戏、计算机动画及计算机仿真等多个领域中。运动捕获(Mocap)数据,作为一组具有时序性的特殊运动序列,能够精准地描述人体在一段时间内的姿态变化。目前,为了保证运动数据的准确性和连续性,捕获设备大多采用高频采样方法进行数据采集,这势必会造成大量数据冗余。为了有效地管理以及重用捕获到的人体运动数据,研究人员的研究重心逐渐从运动数据的获取转向运动数据的处理。一种典型的运动数据处理方法是利用关键帧序列来对人体运动捕获数据进行概括性的描述,使其能够真实地反映原始运动序列所表示的运动语义。有效的关键帧提取方法能减少数据存储容量和加快数据的处理速度,对后续的运动压缩、运动检索和运动合成等实际应用具有重要意义。
近年来,运动捕获数据的关键帧提取方法引起了国内外众多研究学者的广泛关注,代表性的关键帧提取方法主要有两种:等间隔采样法和自适应采样法。等间隔采样法思想简单、易于实现,对节奏平缓的运动序列,关键帧提取的效果优异;但在处理运动节奏有快慢变化的运动序列时,容易产生关键帧冗余或者遗漏现象。相比之下,采用自适应采样法,能在很大程度上避免上述问题的出现。自适应采样法主要有两类:第一类是曲线简化技术[1],其主要思想是把运动序列中的每一帧数据看成高维空间曲线上的一个点,提取曲线上的部分局部极值点作为关键帧。然而,该类方法以简单的欧氏距离度量帧间差异,忽略了运动序列的时序性和运动数据本身的结构特性,容易造成某些关键帧的丢失。文献[2]引入骨骼夹角作为运动特征,提出了一种基于分层曲线简化的关键帧提取方法,具有较强的运动概括能力,但引入的单一几何运动特征集在某些情况下会忽略运动局部细节特性,也可能丢失部分运动节奏突变的关键帧。第二类是聚类技术,文献[3]对序列中相似运动姿态进行聚类,每类的首帧作为关键帧。然而,随着运动数据增大,得到的关键帧可能会有冗余和部分偏差现象。文献[4]则运用过滤技术去除其中一些冗余帧,得到的最终关键帧集合较好地表达了运动序列的内容。针对欧氏距离无法很好地度量帧间差异,一些研究者提出新的度量标准:以人体各关节上总的旋转变化作为帧间距[5],通过比较帧间距的变化情况来确定关键帧;并定义了重建误差作为度量标准[6],较好地实现了数据实时压缩。此外,其它关键帧提取方法还包括:文献[7]则提取以重建误差或压缩率为目标的关键帧集合,具有良好的实时压缩效果;文献[8]结合曲线简化和聚类两种技术的自适应采样方法;文献[9]在分割运动序列排除一些不重要帧的基础上基于尺度不变特征变换提取关键帧,其特征具有很好的鲁棒性。上述方法提取的关键帧虽然能较好地概括某些运动内容,但这些方法没有细致地考虑运动序列的局部拓扑结构特性并常常忽略冗余信息的干扰,以致于提取的关键帧序列在揭示运动精确语义方面有一定偏差。
针对上述问题,一种可行的措施是利用特征选择算法来寻找更具判别性的人体运动特征。遗传算法是一种常用的特征选择算法,如文献[10]利用混合遗传算法直接对运动捕获数据进行选择,其提取的关键帧能较好地概括原始运动序列的内容,但因遗传算法随机产生初始种群,其得到的实验结果具有一定的不稳定性。另外,费舍尔分值FS (Fisher Score)[11]和拉普拉斯分值LS(Laplacian Score)[12]也是两种常用且高效的特征选择方法。作为一种典型的特征选择方法,FS对每个特征独立打分,但容易产生次优子集特征;同时,打分时还需要分类信息,无法直接应用于运动捕获数据。相比之下,LS[12]不必考虑此类问题,其性能优于使用单一方差的特征选择方法,且接近于FS。因此,本文在前期工作的基础上提出了一种基于LS 特征选择的运动捕获数据关键帧提取方法,通过过滤式特征选择方法中的拉普拉斯分值法,关注于运动序列的局部拓扑结构特性,动态选择更具判别性的人体运动特征。实验结果表明,该方法提取的关键帧能很好地描述运动序列的内容,且具有良好的概括能力。
2 Laplacian Score特征选择
LS特征选择是基于拉普拉斯特征映射和局部保留投影LPP(Locality Preserving Projection)提出的一种无监督过滤式特征选择算法[12]。此方法采用样本的局部特征来评价特征集合,认为局部结构特征比全局结构特征更重要且更有效。并且,对于两个样本,如果它们的距离越小,那么属于同类的概率就越大。在采用LS算法进行特征选择时,需优先遵守“局部结构保持”准则。
Lr表示第r个特征,用fri表示第r个样本第i个特征,则第r个样本特征表示为fr=[fr1,fr2,…,frm]T。LS算法描述如下:
(1)对于给定样本X∈Rm×d,构造最近邻图Gx=(V,E)表示样本的局部结构。节点集合V为V=X,节点与节点的连接边E为:E={(xi,xj)|ifxiis connected withxjclosely,i≠j,xi,xj∈V}。G的权重矩阵S∈Rm×m定义如下:
(1)
其中,t为合适的常量;S用于描述样本局部结构特征。
(2)定义D=diag(S1),1=[1,1,…,1]T,L=D-S。
为了选择较好的特征,必须使得目标函数Lr最小:
(2)
其中:
∑ij(fri-frj)2Sij=
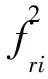
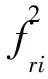
(3)
Var(fr)=∑i(fri-μr)2Dii
(4)
(5)
(3)标准化fr,使得:
1
(6)
计算第r个特征的LS:
(7)
根据计算得出Lr,选取前n(1≤n≤m)个Lr值较小的特征作为合适的样本特征。
3 关键帧提取
3.1 人体骨架模型
人体具有复杂的物理拓扑结构,同时,其运动序列具有时序性。一般来说,人体简化模型可以看作是由关节以及由关节连接的骨骼段组成。如图1a所示,本文采用CMU[13]中ASF格式的人体骨架模型进行人体表示。该人体模型是由31个关节点及关节之间的骨骼构成的层次结构模型,共有62个自由度。自由度分为平移自由度和旋转自由度两种。每个关节有0、1、2、3或6个自由度,其中根关节有6个自由度:3个全局平移自由度和3个局部旋转自由度。在运动数据中,每一帧数据描述一种运动姿态,而每个姿态是由具有62个自由度的骨架模型确定(p∈R62)。那么,运动捕获数据序列是由T个有序的姿态p构成,其中,T表示帧数。

Figure 1 Skeleton model and two kinds of representative features图1 骨架模型及两种代表性的特征
3.2 基于LS特征选择的关键帧提取
骨架特征是运动序列内容中最基本的元素,该特征提取越准确,最终得到的关键帧越精确。另外,人体骨架关于脊椎轴对称,提取的特征应是对称的。基于此,本文选取两种具有代表性、对称性的特征向量:文献[14]中的角度特征向量(见图1b,f1~f8,8个特征向量)和文献[15]中的中心距离特征向量(见图1c,f9~f20,12个特征向量)。
文献[15]提取四肢到根节点的中心距离特征,简单直观,由此方法得到的关键帧序列能较好地表示原运动序列的内容。但是,仅由几个中心距离特征还不能完整地表示一个姿态,鉴于此,本文同时选取了另一种代表性的特征向量,即文献[14]提取的角度特征,共提取了20个特征向量。根据三角形边角边定理,中心距离特征向量和角度特征向量组合后的特征向量能更好地表示人体的空间姿态。这样,从数学上来看,62维数据可降至20维,得到的运动序列可表示为{p}={R20}。由于中心距离特征与角度特征属于不同类型的特征,需对提取的两类特征向量分别做归一化处理,归一化后的运动序列可以表示为{p*}={R20}。
由于组合后的特征子向量间存在相关性,对于运动数据的表示存在冗余,其中某些特征子向量甚至会对关键帧提取造成干扰。此外,较少的特征能减少计算量,提高关键帧的提取效率。为此,使用LS特征选择算法对组合后的特征向量进行筛选,依据其评分结果选取能够较好地揭示局部运动信息并更具判别性的特征子向量(根据多次实验经验,选择前6个特征,效果最优)。接着,基于选择后的特征子向量构建综合特征函数,函数曲线上极值点集合则为候选关键帧集合。由于候选关键帧集合中存在一些时间上相近的或姿态上相似的相邻帧,因此还需要一个精选过程。根据时间阈值约束和姿态相似判别策略,利用改进的k-means算法对候选关键帧集合进行聚类筛选,从而得到最终关键帧集合,其算法流程如图2所示。
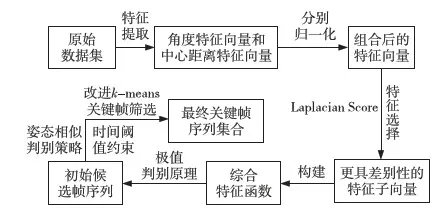
Figure 2 Algorithm flow chart图2 算法流程示意图
具体算法描述如下:
输入:原始数据集,即运动序列amc文件和相应的asf骨架文件以及目标压缩率threshold。
输出:keySet={key(i)|i=1,2,…,round(frames×threshold)},其中keySet为目标关键帧集合,frames为序列的帧数。
步骤1初始化。按照对应的人体骨架模型,将该运动序列转化为矩阵:data∈Rframes×62。
步骤2提取两种代表性的特征向量。基于文献[14,15],分别提取角度特征向量angleFeature及中心距离特征向量centerFeature。
步骤3归一化处理。分别对两种特征向量进行归一化,记作centerFeature*和angleFeature*,其特征向量组合则记为:feature=[centerFeature*angleFeature*]。
步骤4LS特征选择。利用LS对feature打分得到分值向量l∈Rm*1,并选择分值较小的n(n 步骤5生成综合特征函数η。根据l*生成feature*特征权重向量WT=1-l*/sum(l*),其中1=[1…1]T,并对WT进行归一化,生成综合特征函数η=WT·feature*。 步骤6生成初始候选关键帧集合C。基于极值判别原理,选择综合特征函数上的局部极值点,将其对应的帧数依次加入到初始候选关键帧集合C。然后,将等间隔采样法提取的关键帧加入到初始候选关键帧集合C中。 步骤7生成精选关键帧集合C*。根据综合特征函数η以及初始候选帧序列集合C生成的数据集X={x|x(i,1)=C(i),x(i,2)=η(x(i,1))}。根据时间阈值约束和姿态相似判别策略,以等间隔采样法提取的关键帧为初始中心,基于k-means聚类算法,对X进行聚类,聚成round(frames×threshold)类。其中每类的代表帧即为关键帧,构成精选关键帧集合C*,即最终关键帧集合。 采用上述方法提取关键帧,关注运动序列的局部结构特征,较好地表示运动序列中人体运动姿态,且提取的关键帧很好地概括了整个运动序列。 实验采用CMU[13]提供的运动捕获数据序列,采样频率为120帧每秒,自由度为62,在Matlab环境下进行仿真实验,实验中默认压缩率为2%。为测试本文算法的有效性,实验选取三组典型的运动序列Seq1、Seq2、Seq3 (其运动复杂程度和运动语义见表1),并与经典算法进行比较。 Table 1 Sequences used in experiment 相对于运动序列Seq1和Seq2,由于Seq3较长且运动语义复杂程度高,所以更具典型性,在此详细分析其实验结果。根据运动语义可人工地将Seq3划分为跳跃(1~451)和跑步(491~700)两个动作,其中(452~490)为过渡阶段。图3为Seq3的综合特征函数波形图,曲线上凹凸点为本文算法候选关键帧,其中三角标记为本文算法提取得到的最终关键帧序列。由于至今尚没有规范化提取关键帧的统一标准,因此,本文将各算法实验结果与人工提取的关键帧进行视觉上的比较。从图3可以粗略地看出,本文算法最接近于人工提取关键帧,其次是分层曲线简化法,最后是等间隔采样法。表2为Seq3各关键帧提取法实验结果对比。对于表2中子序列过渡部分,关键帧提取方法各提取一帧,人工提取459帧,分层曲线简化法提取的458帧最接近此帧,其次是本文算法提取的464帧,从视觉上看姿态几乎无差异。人工提取的1~126帧间,等间隔采样法提取了55、109两帧,显示了该方法在节奏慢的部分过采样的问题;分层曲线简化方法中提取了12、62和112三帧,有同样的问题;而本文算法只提取了一帧55帧。虽然跑步帧数少于跳跃帧数,但该序列中跑步节奏较跳跃快些,故人工提取关键帧反而比跳跃部分多1帧。对于跑步子序列,等间隔采样法提取4帧,分层曲线简化法提取3帧,而本文算法提取5帧。 Figure 4 Postures corresponding to each algorithm in Seq3图4 Seq3各算法提取的关键帧对应的姿态图 子序列提取的关键帧数及具体的关键帧(帧)跳跃(1~451)过渡(452~490)跑步(491~700)人工提取6(1,126,189, 244,319, 372)1(459)7(515,569,601,624,647,668,700)等间隔采样9(1,55,109,163,217,271,325,379,433)1(487)4(541,595,649,700)分层曲线简化10(1,12,62,112,189,252,316, 367,382,404)1(458)3(559,647,700)本文算法8(1,55,128,168,193,252,326,382)1(464)5(557,593,648,681,700) Figure 3 Key frames extracted from each algorithm in Seq3图3 Seq3各关键帧提取算法提取的关键帧 图4为Seq3序列四种算法提取的关键帧对应的姿态图。从图4中可以看出,人工提取的第二帧关键帧是126帧(姿态描述:双手举起,并超过头顶,跃起),本文算法提取的128帧是时间上和姿态上最接近的关键帧。人工提取的第三帧为189帧(姿态描述:双手自然放下,站立),等间隔采样法没有提取到接近的关键帧,分层曲线简化方法提取的恰好是189帧,本文算法提取的是193帧,虽然相差4帧,但从视觉上看,姿态几乎无差异。由于等间隔采样法的天然局限性,在跳跃部分变化节奏慢,过采样,而在跑步部分变化节奏快,欠采样;分层曲线简化法对原始序列有很好的概括能力,但忽略了一些姿态边界帧,譬如681帧;而本文算法选取的运动特征能较好地保留运动序列的局部结构特征和有效信息。 为定量评价本文算法的有效性,建立两个评价指标:帧间距离误差FD(Frame Distance)和姿态距离误差PD(Posture Distance)。同时,将本文算法得到的关键帧集合F=keySet与人工提取的关键帧mF进行比较。为了保证评价的可信度,本文对实验数据多次人工提取关键帧,取综合结果作为最终人工提取关键帧。其中,(F-mF)表示算法提取的关键帧与最近的人工关键帧的距离,取其平均值来衡量运动序列帧间距离误差FD,姿态距离误差PD则利用Frobenius范数度量。FD、PD及评价函数J分别定义如下: FD=averg(F-mF) (8) (9) J=FD′PD (10) 其中,u为关键帧帧数,v为运动序列的空间维度, ‖*‖F为Frobenius范数,spXyz为原始运动数据转换到欧几里德空间中的高维数据。FD和PD值越小,算法的概括力和表现力越强。 表3为不同算法对Seq1~Seq3序列关键帧提取误差。从其对比数据中可以看出,对等间隔采样法,帧间距离误差FD分别为15、11和18,其准确性很大程度上依赖于运动序列的节奏。对本文算法,帧间距离误差变化不大,其准确性比较稳定,与分层曲线简化法的效果相近。总的来说,本文算法的帧间距离误差和姿态距离误差最小,等间隔采样法的误差最大。主要原因在于等间隔采样法忽略了运动序列的内容,如运动节奏;分层曲线简化法对所有特征进行处理,其中部分冗余子特征干扰了关键帧的提取。 Table 3 Extracted error in different sequences 本文算法考虑了原始运动序列的语义和运动特性,以Seq3为例,图5为Seq3中LS特征选择得到的特征子向量(选取前6个,效果最优),特征子向量的重要性依次为:头部运动角度特征、右臂弯曲程度、左臂弯曲程度、右腿弯曲程度、左腿弯曲程度以及右胫距离特征。本文算法采用LS算法对全部特征进行选择,较好地避免了冗余子特征对提取关键帧的干扰;同时,由于运动序列的固有特性,在较短时间段可能呈现帧间姿态相似性特点,本文算法基于姿态相似判别策略和时间阈值约束,能对候选关键帧进行有效的筛选。 表3中实验结果表明,对于不同运动复杂程度和运动语义的序列,与等间隔采样法和分层曲线简化法相比,本文算法提取关键帧序列最接近于人工提取关键帧,且具有较小的误差率和较高的准确率。 Figure 5 Subfeatures selected by LS in seq3图5 Seq3 LS特征选择得到的特征子向量 从以上对比实验可以看出,本文算法提取的关键帧序列,能较好地弥补等间隔采样法的不足,避免分层曲线简化法的特征干扰问题,对于原始运动序列具有良好的概括性和适应性。综上所述,本文提出的关键帧提取算法是有效的。 为动态选择具备判别性的人体运动特征,本文提出了一种基于LS特征选择的关键帧提取算法。首先,基于两种代表性的特征向量将原始高维运动数据空间映射到低维空间,这样产生的特征数据能很好地保留运动序列的局部结构特征和有效信息。接着,通过LS算法选择组合后的特征向量,构建综合特征函数并依据极值判别原理,得到初始候选关键帧序列。最后,以等间隔采样法提取的关键帧作为初始中心,通过k-means算法去除部分冗余关键帧,以得到最终关键帧集合。与等间隔采样法和分层曲线简化法相比,本文算法提取的关键帧对原运动序列具有更好的概括性、较小的误差率和较高的准确率。在今后工作中,我们将考虑能够较好揭示运动语义的普适特征向量进行关键帧提取,并进一步研究基于提取关键帧的插值效果进行序列拼接,合成满足用户需求的新序列。此外,考虑到动作捕获数据过程中往往不可避免地参杂一些噪声和离群值,下一步的工作是对含有噪声干扰的运动捕获数据做恢复,以改善捕获数据质量,接着基于恢复后的数据提取关键帧序列。 [1] Lim I S, Thalmann D. Key-posture extraction out of human motion data[C]∥Proc of the 23rd Annual International Conference of the IEEE, 2001:1167-1169. [2] Xiao Jun, Zhuang Yue-ting, Wu Fei, et al. A group of novel approaches and a toolkit for motion capture data reusing[J]. Multimedia Tools and Applications, 2010, 47(3):379-408. [3] Liu Feng, Zhuang Yue-ting, Wu Fei, et al. 3D motion retrieval with motion index tree[J]. Computer Vision and Image Understanding, 2003, 92(2):265-284. [4] Liu Dian-ting, Shyu M L, Chen Chao, et al. Within and between shot information utilisation in video key frame extraction[J]. Journal of Information & Knowledge Management, 2011, 10(3):247-259. [5] Shen Jun-xing, Sun Shou-qian, Pan Yun-he. Key-frame extraction from motion capture data[J]. Journal of Computer-Aided Design & Computer Graphics, 2004,16(5):719-723.(in Chinese) [6] Liu Yun-gen, Liu Jin-gang. Key frame extraction from motion capture data by optimal reconstruction error[J]. Journal of Computer-Aided Design & Computer Graphics, 2010,22(4):670-675. (in Chinese) [7] Cai Mei-ling, Zou Bei-ji, Xin Guo-jiang. Extraction of key-frame from motion capture data based on pre-selection and reconstruction error optimization[J]. Journal of Computer-Aided Design & Computer Graphics, 2012, 24(11):1485-1492. (in Chinese) [8] Bulut E, Capin T. Key frame extraction from motion capture data by curve saliency[C]∥Proc of the 20th Annual Conference on Computer Animation and Social Agents, 2007:182-185. [9] Wu Zhen-yu,Wu Rui-qing,Yu Hong-yang,et al.Key frame extraction towards Kernel-SIFT identification[C]∥Proc of 2013 International Conference on Advanced Computer Science and Electronics Information (ICACSEI 2013),2013:163-166. [10] Liu Xian-mei, Hao Ai-min, Zhao Dan. Optimization-based key frame extraction for motion capture animation[J]. The Visual Computer,2013, 29(1):85-95. [11] Gu Quan-quan, Li Zhen-hui, Han Jia-wei. Generalized fisher score for feature selection[C]∥Proc of the 27th Annual Conference on Uncertainty in Artificial Intelligence, 2011:266-273. [12] He Xiao-fei, Cai Deng, Niygoi P. Laplacian score for feature selection[C]∥Proc of Advances in Neural Information Processing Systems, 2005:507-514. [13] CMU graphics lab motion capture database[DB/OL].[2013-10-15]. http://mocap.cs.cmu.edu. [14] Yang Yue-dong, Wang Li-li, Hao Ai-min, et al. Human motion capture data segmentation based on geometric features[J]. Journal of System Simulation,2007,19(10):2229-2234. (in Chinese) [15] Peng Shu-juan. Key frame extraction using central distance feature for human motion data[J]. Journal of System Simulation, 2012, 24(3):565-569. (in Chinese) 附中文参考文献: [5] 沈军行,孙守迁,潘云鹤. 从运动捕获数据中提取关键帧[J]. 计算机辅助设计与图形学学报, 2004,16(5):719-723. [6] 刘云根,刘金刚. 重建误差最优化的运动捕获数据关键帧提取[J]. 计算机辅助设计与图形学学报, 2010,22(4):670-675. [7] 蔡美玲,邹北骥,辛国江. 预选策略和重建误差优化的运动捕获数据关键帧提取[J]. 计算机辅助设计与图形学学报, 2012, 24(11):1485-1492. [14] 杨跃东,王莉莉,郝爱民,等. 基于几何特征的人体运动捕获数据分割方法[J]. 系统仿真学报,2007,19(10):2229-2234. [15] 彭淑娟. 基于中心距离特征的人体运动序列关键帧提取[J]. 系统仿真学报,2012,24(3):565-569.4 实验结果与分析
4.1 实验

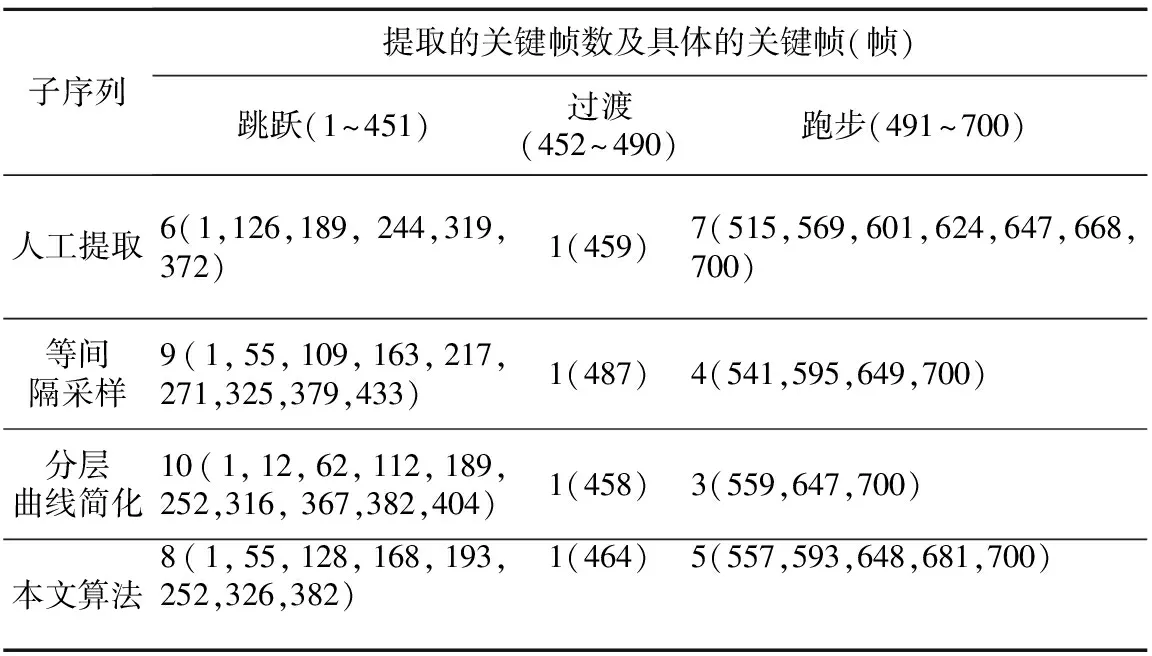
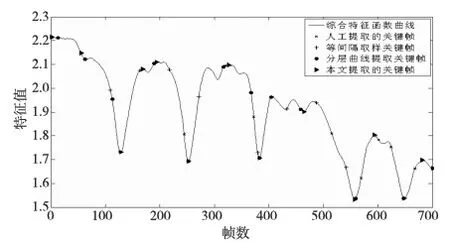
4.2 实验分析
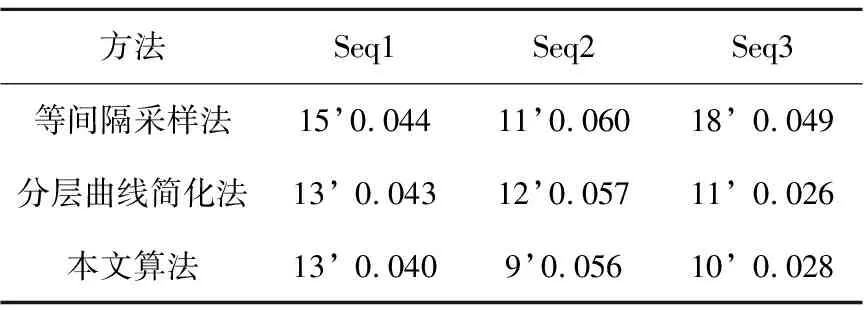

5 结束语
