基于卷积计算的多层脉冲神经网络的监督学习*

张玉平，蔺想红

(西北师范大学计算机科学与工程学院，甘肃 兰州 730070)

1 引言

随着人们对神经网络的深入研究，目前人工神经网络已经发展到了第三代——脉冲神经网络(Spiking Neural Network)阶段[1]。脉冲神经网络应用精确定时的脉冲序列对神经信息进行编码和处理，这种包含时间计算元素的计算模型更具生物解释性，是进行复杂时空信息处理的有效工具[2]。相比传统的基于脉冲频率编码的人工神经网络，基于脉冲精确定时特性的脉冲神经网络拥有更强大的存储和计算能力，它能够模拟各种神经元信息和任意的连续函数，非常适合于大脑神经信息的处理问题[3]。

神经网络目前主要使用两种编码方法：频率编码和时间编码[4]。在频率编码中假设信息是由在某段时间内出现的脉冲数目表示，该方法主要应用于传统的人工神经网络。另一种方法是时间编码，它是应用脉冲的精确时间进行的信息编码，该编码方式已被神经科学的大量实验成果证实。例如，实验证据显示大脑的巨大记忆容量主要依赖于神经信息处理的精确脉冲时间编码机制[5]。此外，一些模式识别问题，例如颜色识别、视觉形态识别、气味识别和声音辨别等，在基于频率编码的人工神经网络模型中不能得到很好的解决，但在基于时间编码的脉冲神经网络中能够得到理想的求解效果[6]。同时，脉冲时间编码还能够减少所需执行给定任务的神经元数量。因此，考虑脉冲神经网络基于脉冲精确定时编码神经信息的特征，构建高效的脉冲神经网络监督学习算法非常关键，同时也是该研究领域的重要问题，日益受到广大研究者的关注。

然而，由于脉冲神经网络模型内在的复杂性和脉冲序列的离散特性，使得脉冲神经网络的监督学习算法构造和实际应用非常困难。Bohte S M等人[7]首次提出了适用于多层前馈脉冲神经网络的误差反向传播算法，称为SpikeProp算法，为了克服神经元内部状态变量由于脉冲发放而导致的不连续性，限制网络中所有层神经元只能发放一个脉冲。其他研究者进一步扩展了SpikeProp算法，给出了对神经元脉冲发放个数不作限制的多脉冲学习算法[8,9]。SpikeProp及其扩展算法是一类数学分析方法，在学习规则的推导过程中，要求所使用的神经元模型中的状态变量必须能够解析，且解析能够用表达式来表示。在最近的研究中，研究者给出了更具生物解释性的脉冲神经网络监督学习算法，能够对脉冲序列复杂时空模式进行学习，主要的算法有ReSuMe[10]、Chonotron[11]、PSD[12]算法等。Mohemmed A和Schliebs S[13,14]基于核函数卷积思想给出了SPAN(Spike Pattern Association Neuron)算法，其主要特点是应用核函数将脉冲序列转换为卷积信号，通过转化后的输入脉冲序列、神经元目标输出和实际输出脉冲序列，应用Widrow-Hoff规则调整突触权值。这些监督学习算法虽然对网络中所采用的神经元模型没有限制，但算法并不具备误差反向传播机制，仅适用于单层神经网络或递归网络输出层突触权值的学习。

本文在SPAN算法的基础上，提出了一种把核函数卷积应用于多层脉冲神经网络的监督学习算法。该算法通过脉冲序列的卷积计算表示形式，将离散的脉冲序列转换为连续函数的分析过程，并解释为特定的神经生理信号。在多层前馈网络结构中，应用梯度下降思想推导得到隐含层和输出层的突触权值学习规则。该算法在多层脉冲神经网络中通过突触权值的调整，能够实现脉冲序列时空模式的学习，并应用于非线性模式分类问题中，具有更高的分类准确率。

2 监督算法的学习规则

2.1 脉冲序列的卷积表示

脉冲神经网络监督学习的目标是对于输入神经元任意给定的脉冲序列模式，通过突触权值的调整，神经元最终输出所要求的目标脉冲序列模式。脉冲序列S={tf∈Γ:f=1,…,F}表示脉冲神经元在区间Γ=[0,T]所发放脉冲时间的有序数列，而脉冲信号用来表示信息或载波，是一种离散信号。其形状多种多样，常见的有矩形波。脉冲序列可形式化地表示如下：

(1)

其中，tf表示第f个脉冲发放时间，δ(x)表示Dirac delta函数，当x = 0时，δ(x)=1，否则δ(x)=0。

由于脉冲序列是由神经元发放脉冲时间所构成的离散事件集合，为了方便分析和计算，选择特定的核函数κ(t)，应用卷积将脉冲序列唯一地转换为一个连续函数：

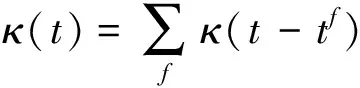
(2)

其中s(t)为公式(1)，通过对脉冲序列基于核函数的卷积计算，可将脉冲序列解释为特定的神经生理信号，比如神经元的突触后电位或脉冲发放的密度函数。该算法中，核函数为κ(t)=eτ-1te-t/τH(t)，H(t)表示Heaviside函数，当x ≥ 0时,H(x)=1，否则H(x)=0;τ是一个实值常数。因此，本文中用卷积的形式表示的脉冲序列为：

(3)

为了分析神经元输入和输出脉冲序列之间的关系，本文使用广义的线性泊松神经元模型(Linear Poisson Neuron Model)[15]。将神经元的突触后脉冲序列So(t)表示为突触前脉冲序列的线性加权形式：

(4)

其中，o表示第o个输出神经元且o∈O；n表示突触前神经元的个数，即输入到神经元脉冲序列的数量；Si(t)为公式(3)表示的突触前脉冲序列；wi表示连接神经元的突触权值。

2.2 网络中权值的调整

(5)

其中，o∈O表示输出层的神经元数量。

为了使网络误差最小化，使用梯度下降方法来调整权值：

其中，η表示学习率,Δw(t)表示误差E(t)在时间t对于突触权值w的梯度下降值。

对于输出层突触权值woh调整这部分，使用梯度下降及链式规则进行推导。突触权值woh随时间更新的公式可表示为：

(6)

公式(6)右边的第一部分可以做如下处理：

(7)

由神经元突触前后脉冲序列的关系公式(4)，公式(6)右边的第二部分可表示为：

这里nh表示隐含层神经元的数目。

于是可以推导出输出层神经元突触权值的调整公式为：

(8)

考虑公式(2)的脉冲序列核函数卷积计算，可将公式(8)重写为如下的表示形式：

(9)

将公式(9)积分，可得到输出层的突触权值总的更新规则为：

对于隐含层突触权值whi调整这部分，误差导数的计算使用类似于输出层的计算方法。

突触权值whi随时间更新的公式可表示为：

(10)

上面公式(10)右边的第一部分可使用链式法则扩展到每个输出神经元，其规则如下：

(11)

公式(11)中右边的第二部分可由公式(4)计算得到：

(12)

将公式(7)和公式(12)代入公式(11)，可得：

公式(10)右边第二部分可推导得出：

这里ni表示输入层神经元的数目。

因此，综合上述公式可得到隐含层突触权值的调整公式为：

将上式积分，可得离线的突触权值更新规则为：

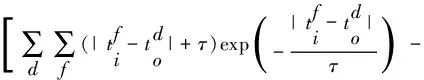
3 实验结果与分析

为了阐述该算法的特征，这里将执行一些仿真实验。在本文中共设计两个实验，第一个实验是学习多个输入脉冲序列模式到单个目标输出脉冲序列的映射，这个实验的目的是验证该学习算法产生脉冲序列的功能。第二个实验是将该算法应用到非线性模式分类问题中，实现对Iris数据集的分类任务，在这个实验中将验证该算法的模式识别能力。

3.1 单脉冲序列的学习

Figure 1 Spike train model图1 脉冲训练模型

从图1中可以看到，在早期的迭代中实际输出的脉冲与期望目标脉冲存在着较大的误差，在随后的迭代中输出的脉冲朝着期望脉冲收敛；注意到在迭代50次内神经元能够非常精确地产生所期望的脉冲输出序列；迭代50次后，在期望的时间内接近目标脉冲的输入脉冲被加强，同时，在不期望的时间内脉冲的输出被抑制，在该实验中，可以推断该学习算法确实能够训练多个随机输入脉冲序列模式映射到一个单目标脉冲序列。

图2表示的是单脉冲序列学习在[0 ms，100 ms]误差的进化过程，其误差值使用实际输出序列与目标序列之间的差值进行计算。该实验迭代100次。从图2中可以看出误差值随着迭代次数的增加而减小，误差函数值在进化开始时，误差值迅速收敛，出现了一个快速减小的过程，迭代到70次后误差值趋于平稳，收敛到一个稳定的值，从图2中可以看出该算法具有较好的收敛性。

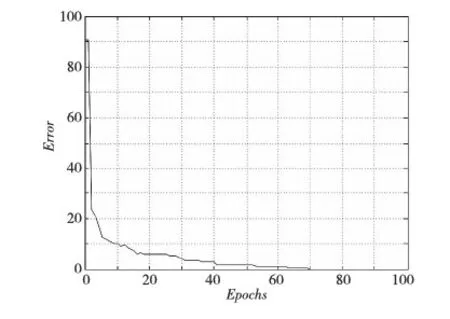
Figure 2 Evolution of error图2 平均误差进化

3.2 分类问题

在这个实验中，本文采用多层前馈型脉冲神经网络结构，并将该算法应用到非线性模式分类问题中，实现对Iris数据集的分类，目的是学会分类三类输入脉冲序列模型。在实验中，从Iris数据集的三类花中每类随机抽取10个样本组成训练集(共30个样本)，每类花中剩余的40个样本组成测试集(共120个样本)，输入特征值采用线性编码方案。

对于每一类输入脉冲序列模型，首先把每个样本的四个特征值分别归一化后线性编码在[10 Hz，40 Hz]的频率。接着把每个频率转化为[0 ms，100 ms]的脉冲序列。然后再把每个样本的四个特征值分别编码成四个线性输入脉冲序列。在Iris数据集中把每一类的输出值1、2和3分别编码成10 Hz、20 Hz和30 Hz的目标脉冲序列。经过学习后，输出神经元为每个分类训练产生一个脉冲序列。本文设定该学习方法在[0 ms，100 ms]进行学习，在学习过程中分别计算输入脉冲序列与三个目标脉冲序列的误差值，根据误差值来确定输入脉冲所属类别。该实验训练100次，在每次训练中都选择不同的随机数初始化突触权重。

图3显示了训练100次后，Iris数据集的训练集在学习过程中三类输入脉冲序列模型各自与目标脉冲序列的平均误差率的进化。在刚开始时误差迅速减小,然后出现了一个波动过程，随后开始稳定下来并且慢慢减小。在分类过程中，一些类的学习误差减小较快，这是由于这些类的分类速度快于其他的类，例如类2。为了测试分类情况，本文分别对Iris数据集的训练集和测试集进行测试。在分类中神经元能够实现训练集和测试集的分类，且训练集平均分类正确率达到94.6%，测试集平均分类正确率达到93.7%，很好地实现了对Iris数据集的分类效果。

Figure 3 Iris training set average error rate evolution图3 Iris训练集平均误差率变化曲线

另外，本文所提算法在Matlab 7.0环境下进行仿真计算，与BP算法对Iris分类结果比较如表1所示。

Table 1 Fisher Iris data classification comparisonunder different learning algorithms

从表1中可以看出，本文所提算法在对Iris这样简单的数据集进行分类时，测试集和训练集在分类正确率上优于传统的BP算法。

4 结束语

应用核函数的卷积计算将脉冲序列转换为连续的函数，通常用来比较和解释脉冲模型，或是在单层网络结构中进行学习。本文针对脉冲神经元精确定时的编码信息特点，提出基于卷积计算的多层脉冲神经网络的监督学习算法，该算法在核函数卷积计算的基础上产生脉冲序列，并将其推广到多层前馈神经网络结构中。在网络中权值的调整是在基本的Widrow-Hoff规则上进行推导的。需要注意的是，核函数是在权值调整之前进行计算的，而在网络中输出层和隐含层的权值是应用梯度下降的方法进行调整的。因此，核函数的应用并不依赖于某种神经模型。在实验部分，构造多层前馈网络结构，实验的第一部分，其结果显示应用该算法能够产生预期的脉冲序列，实验的第二部分，应用该算法对Iris数据集进行分类测试，并对测试结果进行了分析，实验结果证实了该算法的有效性。

作为未来的研究工作，该学习算法可应用到真实世界的时间计算任务中。可继续学习使用该算法作为液态机制的读出函数。并且，可构造递归结构的脉冲神经网络，进一步研究将该算法应用于该网络结构中的可行性，丰富递归脉冲神经网络的监督学习算法。研究该算法在线学习的可行性及动态突触和LIF神经元参数关联的效果。

[1] Gerstner W,Kistler W M.Spiking neuron models:Single neurons,populations, plasticity[M]. Cambridge:Cambridge University Press, 2002.

[2] Bohte S M. The evidence for neural information processing with precise spike-times:A survey[J]. Natural Computing, 2004, 3(2):195-206.

[3] Ghosh-Dastidar S, Adeli H. Spiking neural networks[J]. International Journal of Neural Systems, 2009, 19(4):295-308.

[4] Quiroga R Q,Panzeri S.Principles of neural coding[M]. Boca Raton, Florida:CRC Press,2013.

[5] Szatmry B , Izhikevich E M. Spike-timing theory of working memory[J]. PLoS Computational Biology, 2010, 6(8):1.

[6] Hu J, Tang H, Tan K C, et al. A spike-timing-based integrated model for pattern recognition[J]. Neural Computation, 2013, 25(2):450-472.

[7] Bohte S M, Kok J N, La Poutré J A. Error-backpropagation in temporally encoded networks of spiking neurons[J]. Neurocomputing, 2002, 48(1-4):17-37.

[8] Ghosh-Dastidar S, Adeli H. A new supervised learning algorithm for multiple spiking neural networks with application in epilepsy and seizure detection[J]. Neural Networks, 2009, 22(10):1419-1431.

[9] Xu Y,Zeng X,Han L,et al.A supervised multi-spike learning algorithm based on gradient descent for spiking neural networks[J]. Neural Networks, 2013, 43:99-113.

[10] Ponulak F, Kasinski A. Supervised learning in spiking neural networks with ReSuMe:Sequence learning, classification, and spike shifting[J]. Neural Computation, 2010, 22(2):467-510.

[11] Florian R V. The Chronotron:A neuron that learns to fire temporally precise spike patterns[J]. PLoS One, 2012, 7(8):e40233.

[12] Yu Q, Tang H, Tan K C, et al. Precise-spike-driven synaptic plasticity:Learning hetero-association of spatiotemporal spike patterns[J]. PLoS One, 2013, 8(11):e78318.

[13] Mohemmed A, Schliebs S. SPAN:Spike pattern association neuron for learning spatio-temporal spike patterns[J]. International Journal of Neural Systems, 2012, 22(4):1250012.

[14] Mohemmed A, Schliebs S, Matsuda S, et al. Training spiking neural networks to associate spatio-temporal input--output spike patterns[J]. Neurocomputing, 2013, 107:3-10.

[15] Gütig R, Aharonov R, Rotter S, et al. Learning input correlations through nonlinear temporally asymmetric hebbian plasticity[J]. The Journal of Neuroscience, 2003, 23(9):3697-3714.