外弹道可视化仿真研究与实现*

张进强，蒋夏军

(南京航空航天大学计算机科学与技术学院，江苏 南京 210016)

1 引言

长期以来我军对炮弹的试验，尤其是针对炮弹外弹道的试验，仍以实弹射击为主。但是，实弹射击试验本身存在着试验周期长、成本高、样本数量少等特点，已经不能完全满足当前信息化靶场试验鉴定技术要求。当前对于炮弹外弹道的研究以数据处理为主，缺乏以动态实时直观的仿真方式对外弹道进行分析和处理。随着计算机软硬件的发展及图形处理能力的增强，可视化仿真技术渐渐在军事仿真领域中得到广泛的应用。

目前，在可视化仿真方面的研究受到越来越多的关注，国内外已有的研究工作主要体现在可视化的分类和可视化的实现方面。前者主要从分类的角度来研究各种具体可视化的方法，后者主要从可视化实现的角度、可视化的真实感及机器的负载来讨论。从可视化的分类角度展开的研究中，文献[1]介绍了科学技术可视化、数据可视化、信息可视化和知识可视化等分类和研究比较。文献[2]从文献分类角度介绍了上述四种方法，并对四种方法进行了分析研究及方法评估。文献[3]分别从处理对象、数据类型及可视数据分析技术对可视化进行分类，分析各自的区别及使用场合。上述仅对可视化方法进行研究比较，但都没有对相关可视化技术进行深入研究。

在技术实现的角度展开的研究中，文献[4]使用“开放图形库”(OpenGL)结合C++构建三维图形开发环境中，是一个高性能的图形开发软件包，但开发难度大、周期长。文献[5]在VS2008开发环境下使用WPF和3DS MAX实现虚拟现实技术。WPF作为一套统一图形化系统，融合在.NET开发环境，开发简单、快速，但不能满足多平台和通用性需求。文献[6]结合Microsoft Visual Studio .NET2005和VTK开发了三维可视化系统，提出算法精度与绘制速度相互制约，VTK跨平台、支持并行处理、执行效率高但归因于二次开发，无法操控实时数值仿真的数据。

如今，三维视景仿真技术日渐成熟，加之Matlab强大的数值运算能力和二、三维图形显示优势。针对现有工作存在的一些不足，本文提出对模型实现数值仿真驱动视景仿真，即通过数值仿真得到的飞行数据实时驱动二维、三维图形相结合的视景仿真，以此来全面、直观地观察弹丸在空中的实时飞行姿态、运动轨迹及其落点的散布情况。

本文结构安排如下：第2节主要对仿真数学模型进行介绍，其中包括：外弹道数学建模和随机风影响的落点散布数学模型；第3节主要介绍仿真的实现方法，包括数值仿真和视景仿真。在数值仿真部分，介绍了微分方程的各种数值计算方法，分析各种方法的精度和时耗。在视景仿真部分，创新性地提出图表相结合的三维视景仿真，并分别介绍了在C#环境下引用CsGL.dll构建OpenGL三维图形开发环境和Matlab&C#三维网格坐标轴的混编；第4节是应用案例；第5节是本文的总结。

2 数学模型介绍

以炮弹外弹道方程组为基础对外弹道曲线进行拟合，以蒙特卡洛法为基础进行炮弹落点散布值的求解。

2.1 外弹道数学建模

目前常用的外弹道方程组主要有质点弹道方程组和刚体弹道方程组。其中，刚体弹道方程组虽然计算精度高，但其计算复杂，运算时间过长，影响系统反应时间，不能很好地满足实时性要求。因此，在考虑计算精度和计算速度的基础上，本文采用质点弹道方程组。

2.1.1 弹丸质心运动模型

由于弹丸在飞行过程中会受到起始扰动、阵风、推力偏心、质量分布不均衡、弹重偏差及气象偏差等各种因素的影响，从而使弹道轨迹及落点的预测变得复杂无序。为了使外弹道方程简单易懂，作出如下假设：

(1)整个飞行过程中，弹丸的章动角δ恒为零；

(2)弹丸的外形和质量分布是轴对称体；

(3)射击场所地面是平面；

(4)重力加速度g方向铅直向下，且大小不变；

(5)忽略由于地球自转而产生的作用在飞行炮弹上的科氏惯性力。

在上述基本条件假设下，根据外弹道理论，考虑弹道条件(初速、弹重和药温)和气象条件(气温、气压、纵风和横风)非标准时的弹丸质心运动方程组，由下式表示[7]：

(1)

其中，t为弹丸飞行时间，x、y、z为弹丸离开炮口后在飞行过程中的坐标(x,y,z)的水平分量、垂直分量和横向分量；c为弹丸系数；θ为速度V的水平倾角；Vx、Vy、Vz分别为弹丸速度V在水平、垂直和横向方向上的分量；g为重力加速度；H1(y)为空气密度函数；G(v,c1)为空气阻力函数。积分的初始条件为：t=0,vx=v0cosθ,vy=v0sinθ,vz=0,x=y=z=0。

其中阻力函数为[7]：

G(vr,c1)=4.737×10-4vrcxon(Ma),

Ma=vr/c1

(2)

2.1.2 弹道条件

弹道条件非标准主要包括初速、弹重和药温等。弹道条件非标准可折合成初速和弹道系数两个参量的变化问题，因此可直接应用标准条件下的弹丸质心运动微分方程组，只是决定空气弹道的三个参量Cb、V0、θ0中的Cb和V0分别改为Cb+ΔCb和V0+ΔV0,其中ΔCb和ΔV0为弹道条件非标准时的折合量。

2.1.3 气象条件

气温非标准条件规定，非标准气象条件下气温随高度变化服从标准分布，结合我国地理条件，改进气温标准模型得到非标准气象条件下气温随高度变化的规律满足如下模型[8]：

(3)

其中，Tvon为标准条件下的地面气温，Tv1表示各高度处的不符合标准定律的气温,ΔTv为实际温度与标准定律对应的气温偏差；G1=6.328×10-3K·m-1,B1=1.172×10-6K·m-2。

当气温、气压不符合标准定律时，气压函数的表达式为[8]：

(4)

其中，P0为地面气压值；π1(y=9300)、π2(y=12 000)分别表示气压函数在9 300 m和12 000 m时的值；A1=230 K。此时的空气密度函数用H1(y)表示，其计算公式[8]为：

(5)

同理，当气温不符合标准定律时，对应的声速也不符合标准定律，其计算公式为：

(6)

所以，气温、气压非标准时的弹道方程可直接应用标准条件下的弹道方程进行计算，只是以H1(y)代替H(y)、以实际声速C1(y)代替标准声速C(y)而已。在式(1)结合式(2)～式(6)的基础上，针对选定的高炮弹药，在气温、气压、射角及横侧风一定时，通过数值计算方法，即可确定以时间t为自变量的任意点的射击诸元。

2.2 落点散布数学建模

随机干扰(如随机风和起始扰动)是影响炮弹落点散步的重要因素，将风场作为典型的随机过程，建立随机风场的数学模型并结合外弹道数学模型，采用经典的统计实验法——蒙特卡罗法进行随机风作用下炮弹落点散布的模拟代替射击实验，以随机风影响下炮弹落点模拟结果的均值和方差反映实际射击过程的散布特征，以此分析随机风对炮弹落点散布的影响。

由于风力和风向千变万化，无法事先预知，因而在实际工作中主要考虑横风、侧风和铅直风，除特殊地区(山谷)外铅直风一般较小不予考虑。

仿真思想主要是对于随机条件，用符合正态分布的伪随机数表示，然后将伪随机数代入弹丸的外弹道方程中进行计算，最后通过二、三维坐标图实现弹道飞行轨迹及落点的可视化。

随机仿真可得各发炮弹的纵向和横向落点坐标，分别记为(x1,x2,…,xn)和(z1,z2,…,zn)，n为仿真次数。炮弹的纵向、横向平均落点坐标，散布中心的差值分别为[9]：

通过对仿真结果的统计分析，可以求出落点与目标的射程及侧偏偏差的均值，依据射表查找相应的修正量，从而提高炮弹的射击精度。

在正确的外弹道模型及随机风的数学模型的基础上，利用蒙特卡罗仿真技术预测弹丸落点的方法，在测得随机风的实时状态下，通过模拟系统得出弹丸落点的方差和数学期望，分析风对弹丸落点的影响，得出对炮弹射击精度影响的强弱程度。对火炮而言，最重要的弹道诸元是炮弹的射程及侧偏。其中炮弹的射程主要由初速、射角和纵风引起的，而侧偏则由横风引起。

3 仿真实现

3.1 数值仿真

求微分方程的解有两种方法，对于一些典型的微分方程(如线性方程、某些特殊的一阶非线性方程等)可以求出其解析解，并根据初值的条件给出表达式，但遇到复杂的微分方程模型时，解析解很难求出，因此只能求方程的近似解或数值解。目前微分方程常用的数值计算方法主要有三种:欧拉法、改进的欧拉法及龙格-库塔法。

经测试，将上述三种方法代入质点弹道方程组，求得各自的运算时间及精确度，如表1所示。

Table 1 Comparison of numerical calculation methods

因此,弹道方程的求解采用四阶龙格-库塔法，仿真系统中步长h取0.05 s，在保证有较好稳定性的前提下整个外弹道仿真过程的累积误差在0.1 m以内。而且四阶龙格-库塔法的计算速度较快，这使得外弹道的仿真过程具有较好的实时性，能较好地满足军事打击高精度和实时性的需求。

3.2 三维空间视景仿真

3.2.1 OpenGL三维场景仿真

若想逼真地模拟实弹飞行场景，视景仿真模块必须进行实时的数据更新，如实时的炮弹的速度、坐标、射角及偏流等，即用数值仿真来驱动视景仿真。但同样也需要建立起相应的逼真三维场景，包括靶场及炮弹的飞行过程还有落地的爆炸场景等。由于图形的绘制效率和绘制效果是相矛盾的，提高真实感，势必就会降低仿真场景的绘制速度，从而降低了图形的实时性。因此，只有在满足实时性的基础上，尽可能地获得高质量的绘制效果。

本系统建立炮弹三维空间模型，在屏幕上显示具有三维特效的炮弹及靶场，在此基础上进行炮弹的空中飞行姿态的动态显示。具体实施步骤如下：首先利用3DMAX生成炮弹的3D模型；其次利用C#开发环境调用CsGL.dll构建OpenGL运行环境模块；调用OpenGL建立炮弹的三维空间模型[10]，根据数值仿真计算得到的飞行仿真数据构建炮弹的空中飞行过程(飞行姿态、飞行轨迹)；依照贴图坐标构建靶场背景。

3.2.2 C#构建OpenGL开发环境模块

用第三方插件CsGL，关键是使用其提供的两个DLL：csgl.dll和csgl.native.dll。在一个C#项目中，用“项目”→“添加引用”→“浏览”找到csgl.dll引用。在需要使用OpenGL函数的cs文件的声明中,添加：using CsGL.OpenGL。并做以下重构：

protected override voidOnSizeChanged(EventArgse){ }/*窗口大小变化时调用*/

public override voidglDraw(){ }/*OpenGL初始化，绘制想要画的图形*/

protected override voidInitGLContext(){ }/*绘制环境初始化*/

3.2.3 炮弹模型的建立及绘制

采用3DMAX建立炮弹立体模型及模型的贴图坐标。模型相对容易建立，为使模型具有真实的视觉效果，可以对模型加上各种独有的材质，如颜色、反色特性等效果。OpenGL载入3D模型文件时，因对象的外部形状主要是靠三角形来模拟的，所以需先定义一系列结构体来存放模型的点、三角形及贴图的坐标和材质等。然后，参照结构体读入的信息，用OpenGL绘图命令根据得到的各种结构体数组来进行绘制，并通过颜色、材质及纹理等深化效果。载入后的模型的大小和位置跟预期的效果不一样，这时需采用GL.glTranslate()平移函数、GL.glRotate()旋转函数及GL.glScale()缩放函数来调整模型。

3.2.4 炮弹的飞行仿真

炮弹的飞行仿真在视景系统中模拟导弹的四自由度，包括三维空间位置坐标(X,Y,Z)及射角(θ)的实时变化。于是炮弹的飞行仿真可以通过添加定时器实时地更新坐标和射角并调用GL.glTranslate()平移函数、GL.glRotate()旋转函数及SwapBuffer()双缓冲函数来实现炮弹的飞行仿真过程。

3.2.5 靶场背景的绘制

背景环境主要包括天空和地面，本文主要采取了纹理映射的方法，选择近似的图片作为纹理，通过载入图片、定义纹理及根据几何坐标映射来得到三维场景。对于可视化仿真要求不太高的场景，可以直接使用纹理映射，操作方便且速度快。

3.3 Matlab三维空间坐标轴的绘制

Matlab是高级工程计算软件，程序可移植性高，不仅具有强大的数据可视化功能，还涵盖二维和三维的可视化、图像处理、动画及表达式作图。C#语言简单、功能强大、类型安全，可实现应用程序的便捷开发，但作图操作繁琐复杂。因此，C#和Matlab混编可以扬长避短。

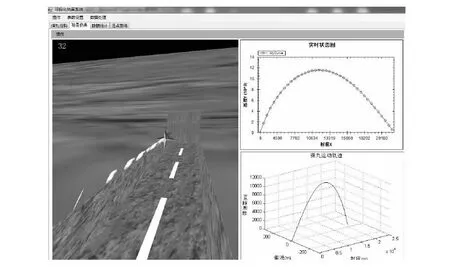
Figure 1 Visual simulation of trajectory图1 外弹道视景仿真

本系统主要利用Matlab绘制三维空间网格坐标轴并能动态显示弹道的飞行轨迹，达到视景仿真与曲线模拟的同步。具体实施步骤如下：首先通过Matlab的m文件来编译生成.NET的dll文件[11]；其次C#调用生成的dll文件，以数组的方式传入三维空间坐标(X,Y,Z)及时间t，Matlab利用得到的坐标数据进行实时绘图。

3.3.1 Matlab生成dll文件

在Matlab的Command Window中输入deploytool，产生deployment tool配置窗口，选择Matlab Builder NET选项卡，新建工程并添加m文件，编译成功即可得到dll文件。dll文件为接口，它实际上不含任何实现，都是调用另一个.ctf文件来完成具体的功能。

3.3.2 C#调用dll文件

添加对MWArray.dll和生成dll文件的引用，通过实例化MWNumericArrayMX、MY、MZ和T，将数值仿真计算所得的空间坐标及对应的时间t以数组形式传给MX、MY、MZ和T并将实例数组传入Matlab中的绘图函数。其中，MWNumericArray是MWArray和C#中数据的中间类，C#与Matlab之间传递参数需用MWNumericArray转换。

4 应用案例

依据上述外弹道、落点散布模型，以某型火炮为例，使用C#语言编制弹道程序，结合Matlab混编实现三维坐标轴的作图及数值计算，并用CsGL实现空间视景的仿真，可更直观地了解整个飞行过程及落点的散布。

4.1 炮弹的数值仿真

数值仿真计算输入数据包括：初始速度、空间坐标、初始攻角、温度偏差及横风侧风等。

初始条件为:V0=900 m/s,x=y=z=0,θ0=45°，tem=3,wx=1,wz=1。经计算，炮弹飞行80 s，射程达到20 785.87 m，侧偏50.15 m，与所提供的实验数据相符。

4.2 外弹道视景仿真

如图1是根据上述初始条件经过数值计算得到的飞行数据实时绘制的炮弹射击场景，图1的左侧部分是炮弹射击的视景仿真，右侧是由Matlab构建的二、三维坐标轴同步曲线模拟。图2根据实时的飞行数据，通过三维仿真模拟出炮弹的初始状态以及15 s、37 s、60 s和结束时的状态。可以根据炮弹的飞行姿态，判断炮弹的飞行稳定性,由图2可看出，炮弹在飞行的过程中，没有发生翻倒，因此炮弹的飞行较稳定。

实际仿真时帧率是使用Fraps软件进行监测求得，约为32 fps，即大约31.2 ms完成一帧。而数值仿真部分使用龙格-库塔法，外弹道方程组运算时间约占16 ms，视景仿真部分引用CsGL.dll在C#下构建OpenGL环境，三维处理时间约占11 ms。因此，该系统既取得了较高的运算精度，又满足了实时性需求。

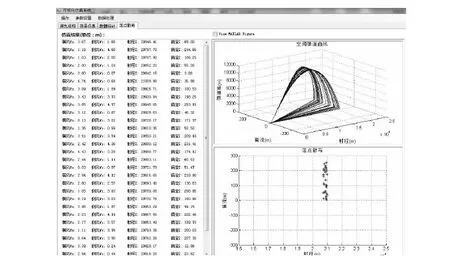
Figure 3 Fall point of shell图3 炮弹的落点散布

Figure 2 Flight posture of shell图2 炮弹飞行姿态

4.3 落点散布仿真

数值仿真计算输入的数据包括：初速、射角、空间坐标、随机风的分布参数及模拟次数。初始条件为：V0=900 m/s,θ0=45°，x=y=z=0,wx(μ,σ2)=(1,5),wy(μ,σ2)=(1,5),times=30。

如图3所示，左侧为仿真30次的结果，包括横风、侧风以及在此影响下的射程及偏流。右侧为模拟30次射击的二、三维落点散布图，从落点散布图可以看出，侧风对炮弹落点的影响远大于横风；炮弹的射程越远，侧风的影响越大。

5 结束语

本文实现了基于数值仿真实时驱动的弹道可视化仿真平台，借助此平台对炮弹的飞行轨迹、实时运动姿态及落点散布进行了仿真研究。研究表明，弹道可视化仿真系统可对炮弹运动状态进行实时的计算及在三维场景中实时显示其运动状态，较完整地反映了炮弹的运动规律，操作简便，画面流畅；落点散布仿真根据添加的随机风条件，得出侧风对炮弹落点的影响远大于横风，炮弹的射程越远，侧风的影响越大，为实弹射击的修正提供参考。

通过添加内弹道模块及毁伤分析模块，此仿真系统可以扩展为全弹道的仿真系统。此仿真方法也可用于火箭、导弹等武器的仿真。

[1] Zhang Zhuo,Xuan Lei,Hao Shu-yong.Study and comparison on visualization technology[J].Modern Electronics Technique,2010,33(17):133-138.(in Chinese)

[2] Liu Bo,Xu Xue-wen.Comparison of the visualization taxonomy[J].Journal of Intelligence,2008,27(2):28-30.(in Chinese)

[3] Zhu Yao-hua,Hao Wen-ning,Chen Gang.The summary of visualization theory[J].Computer Knowledge and Technology,2012(6):1.(in Chinese)

[4] Cai Hua,Lu Jing-chao,Xiao Gang.Real-time 3D animated flight simulation based on OpenGL[J].Computer Simulation,2007,24(10):28-30.(in Chinese)

[5] Yang Chao,Xu Xiao-long,Yu Kun,et al. 3D visual control system of underwater vehicle[J].Computer Simulation,2012(4):185-188.(in Chinese)

[6] Schroeder W J. The visualization toolkit users’ guide[M]. New York:Kitware Inc, 2001.

[7] Guo Xi-fu,Zhao Zi-hua.Theory and application of fire control ballistic model[M].Beijing:National Defence Industry Press，1997.(in Chinese)

[8] Zhao Xin-sheng,Shu Jing-rong.The theory and application of ballistic calculation[M].Beijing:Weapon Industry Press，2006.(in Chinese)

[9] Wang Xin,Zhang Feng-ge,Yao Jun,et al.Analyze effect of random wind on shell distribution of rocket using Monte-Carlo method[J].Journal of Projectiles, Rockets, Missiles and Guidance,2009,29(1):198-201.(in Chinese)

[10] The studio of peace dove.OpenGL advanced programming and visualization system[M].Beijing:China Water Power Press,2005.(in Chinese)

[11] Phan J.MATLAB+C#+Book[M].Colorado:LePhan Publishing, 2004.

附中文参考文献：

[1] 张卓，宣蕾，郝树勇.可视化技术研究与比较[J].现代电子技术，2010,33(17):133-138.

[2] 刘波，徐学文.可视化分类方法对比研究[J].情报杂志，2008,27(2):28-30.

[3] 朱耀华，郝文宁，陈刚.可视化技术简述[J].电脑知识与技术，2012(6):1.

[4] 蔡华，卢京潮，肖刚.基于OpenGL的飞行实时三维动画仿真[J].计算机仿真，2007,24(10):28-30.

[5] 杨超，徐筱龙，余琨，等.水下机器人三维可视化控制系统[J].计算机仿真，2012(4):185-188.

[7] 郭锡福，赵子华.火控弹道模型理论及应用[M].北京：国防工业出版社，1997.

[8] 赵新生，舒敬荣.弹道解算理论与应用[M].北京：兵器工业出版社，2006.

[9] 王欣，张凤阁，姚俊，等.蒙特卡罗法分析随机风对火箭弹落点散布的影响[J].弹箭与制导学报，2009,29(1):198-201.

[10] 和平鸽工作室.OpenGL高级编程与可视化系统开发[M].北京：中国水利水电出版社，2005.