多表达式程序设计的新型评估方法*

郑秋生，何 锫,2,3，李 骥

(1.长沙理工大学计算机与通信工程学院，湖南 长沙 410114;2.广州大学计算机科学与教育软件学院，广东 广州 510006;3.北京大学高可信软件技术教育部重点实验室，北京 100871)

1 引言

遗传程序设计GP(Genetic Programming)[1]是重要的自动程序设计方法，包括线性与非线性表示两类。多表达式程序设计MEP(Multi Expression Programming)、基因表达式程序设计GEP(Gene Expression Programming)、文法演化GE(Grammatical Evolution)以及Hoare语义型遗传程序设计等都是线性表达的遗传程序设计方法[2～9]，它们在多目标优化、金融预测、海量数据分析、软件工程、信息安全等领域都得到了广泛的应用[6, 10]。

与传统GP相比较，MEP等线性表达的GP(某些文献也将线性表达的GP简称为线性GP)既便于个体表示、遗传操作，又易于描述复杂结构和实现，因此自提出以来一直很受关注。然而一切GP都以遗传算法[11]为基础，因而转换、评估工作十分繁复，除要将个体的树型/线性表示方式转换成相应的表现型外，还要执行、测试所得的近似解以确认它的合适程度。如此一来，评估(某些语义计算甚至一个小小的步骤就得耗费数十小时以上)等的计算耗费了大量的时空资源，成为GP研究的挑战性问题[12]。

本文拟就评估问题对MEP做深入探讨。先系统化分析它的表示、评估过程中重复计算现象的根源所在，而后给出规避这些问题的理论依据、实际解决方案。因无须重复计算相同的语义工作，新方法在演化效率上有了显著提高。

2 背景和相关工作

多表达式程序设计[3,6,9]作为线性表达的遗传程序设计方法,主要通过将搜索目标分为基因型与表现型两个层面来规范求解过程。由于引入了双层概念，MEP等线性表达方法的评估须先履行两型间的转换，而后执行、测试表现型所刻画的程序。

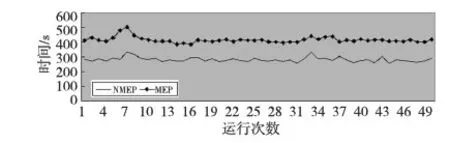
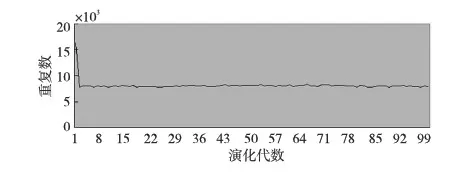
MEP的个体可以表示为线性序列c1,c2,…,cn，其中ci(1≤i≤n)或取自由常量、变量组成的终端集，或取自函数集F，当然此时须依函数的数目以及此前获得的cj(1≤j

Table 1 MEP individual representation

表1中基因1对应的表现型或表达式为a；基因2对应的表达式为b；基因3的表达式为a+b；基因4的表达式为a；基因5的表达式为b×(a+b)；基因6的表达式为(b×(a+b))+a。由此可见，语义的重复计算现象会充斥评估过程，这在MEP里尤为明显。

有关MEP的算法流程如下所示(读者也可以参见文献[3,6,9])：

(1)随机产生一个个体种群；

(2)评估种群中的个体，若满足评估标准、精度或算法终止条件，则停止，最佳个体所表征的解即为所求目标；

(3)若不满足终止条件，则在当前种群上实施杂交、变异等遗传操作以期获得新的种群；

(4)转第(2)步，反复迭代。

MEP的应用[6,9,13～20]概括地讲涵盖数字电路设计、天线设计、符号回归、金融预测与建模、分类、数据分析、入侵检测、决策支持系统、算法设计以及TSP求解等领域。图像配准是利用图像序列实施3D重建的关键任务。文献[17]将这一难题归结为面向特征点的公式发现问题，尝试采用MEP求解。 文献[13]等则探讨了MEP等诸多线性表达的GP在基本入侵检测方面的应用。Alavi A H团队[18～20]解决实际工程应用问题多次采用了MEP。如他们在文献[18]中借助MEP对沥青混合材料的永久变形进行分析；在文献[19]中对土壤液化的评估实施MEP建模。MEP在国内也得到了关注。文献[14，15]等充分考虑GEP、MEP的优势，在个体表示、解读方面做了努力，提高了性能。

综上所述，MEP应用面很广，是解决数据分析、实际工程应用问题的有力工具。然而，MEP与其他GP家族成员一样，也有计算量大、评估耗时的不足。鉴于目前直接改进其评估工作的研究尚不多见，以下拟系统深入地分析个体表示，尝试规避评估过程凸显的重复计值现象，从而提高算法性能。

3 MEP中的重复评估问题

MEP实质是以一定法则不断改变、演化产生新的个体集(也叫种群)的方式来获取问题的解的。从第2节的表1易见，个体的评估会出现大量重复计值现象。本节将深入分析MEP算法模型上的这一问题，指出重复计值现象产生的充分条件和理论计算依据。

定理1设MEP的函数集和终端集分别是F、T，T中终端符的个数为|T|，则染色体中基因个数多于|T|时，必有重复运算。

定义1(等型基因) 设I是MEP系统中长度为d的个体(染色体)，I中第d1、d2(1≤d1,d2≤d)两号基因等型，如果它们所表征的表现型或抽象语法树一致。

定理2设MEP的函数集和终端集分别是F、T，那么评估个体I的长为d的前缀片段(个体前d个基因构成的基因片段)所需的运算量总数，记为N(T,F,I,d)，可由式(1)获得。

(1)

其中,di是基因在个体I中的下标。

证明施归纳于个体前缀基因片段的长度d如下：

(1)归纳基始：d=0或1时，结论显见成立。

(2)归纳论证步骤分两步进行。

①当第d个基因为终端符时： 评估d个前缀基因的总运算量N(T,F,I,d)实质是在前d-1个基因评估运算量基础上增加了一次常量提取运算，因而结论成立，符合公式描述。

②当第d个基因为函数运算f(d1,d2,…,dm)时：d个前缀基因的总评估运算量N(T,F,I,d)应包括前d-1个基因的评估运算量与f(d1,d2,…,dm)本身的运算量两部分。据归纳假设，前者是N(T,F,I,d-1)，后者宜为第d1,d2,…,dm个基因的评估运算量加上一次m元运算f(d1,d2,…,dm)。又对任意i(1≤i≤m)，第di个基因本身的评估运算量可借助归纳假设和总运算量概念表达为：N(T,F,I,d)-N(T,F,I,di-1)。故此结论成立。

□

为方便理解，表1同时给出了染色体前缀运算总量的计值示例。由定义1易见，基因间的等型关系是一种等价关系。下面的定理3将着力回答评估中的重复运算问题。

证明需注意三点：

(1)等型基因类中的元素仅需实际计算一个(比如该类中被第一个分析和发现的元素)。

(2)实际计算等型基因类中的一个元素时，涉及F∪T上符号所表征的计值运算仅有一次。因为参与复合运算的子树是低深度的子树，其计值早在低深度基因类分析过程中已完成，可以直接引用(不涉及F∪T中元素所明确表示的运算)。

(3)关于深度为1的等型类的计值问题，这里按计值一次的方式处理(涉及到T中符号，有可能存在某些转换)，其它重复现象可以通过引用获得(不必做有关转换)。

至此，我们分析了MEP的重复计值问题。它们包括个体内与种群中个体间的重复计值现象，其中后者较为隐蔽。下节将据定理3等结论给出去除重复计算现象的具体技术方案。实际应用过程中，定理3可以施用于演化过程产生的所有种群和个体，这只需将定理中的d视为演化过程中所有个体首尾衔接形成的大个体即可。

4 新型MEP算法及评估

依据以上定理，本节介绍具有去除重复运算功能的评估方案：处理单个基因的算法NMEP及嵌入NMEP的MEP演化算法。

算法NMEP基本思想：通过不断构建等型基因有向图Q(V，E)来识别重复的基因，从而避免重复计算。V是顶点集，E是有向边集，V中每个顶点有编号且对应一个基因，并存储该基因的信息。

算法NMEP

输入：基因g。

输出：基因g在V中的相关顶点编号及g的其他信息。

步骤1本步骤只在MEP初始化种群之前执行一次。初始化等型基因有向图Q(V，E)：终端符集T={z1,…,zk}中每个终端符代表的基因g1,…,gk均属不同等型基因类，故在V中创建它们对应的顶点v1,…,vk(下标1,2,…,k是顶点在V中的编号，下同)，并对所有顶点从1开始依序编号。将基因g1,…,gk所涵盖的语义动作及其基因信息分别写入v1,…,vk顶点中。num_gene等于V中顶点数。

步骤2演化过程中，如果基因g取自T中终端符，由于步骤1已对T中所有终端符进行处理，则直接找到V中与基因g同属一个等型基因类的基因g′对应的顶点v′，输出v′的编号及其基因信息。

步骤3如果基因g是函数形式(pg，s1,…,sn)，其中pg是操作符，s1,…,sn是它的参数，s1,…,sn所对应的基因gs1,…,gsn必然已被处理，找到基因gs1,…,gsn在V中对应的顶点编号a1,…,an。对算法中的操作符需要考虑交换率时，执行步骤3.1、步骤3.3和步骤3.4；不需要时，执行步骤3.2、步骤3.3和步骤3.4。

步骤3.1当算法适用交换率时，如果pg满足交换率，则需要将a1,…,an按一定顺序排列成标准序列(本算法以a1,…,an的升序排列结果作为标准序列t1,…,tn)，如此便于在步骤3.4的操作中查找满足与基因g重复条件的基因；否则，如果pg不满足交换率，把a1,…,an赋值给t1,…tn；最后，找到顶点vt1。

步骤3.2当算法不适用交换率时，把a1,…,an赋值给t1,…,tn；最后，找到顶点vt1。

为此，嵌入NMEP进行评估去重的算法可重新表述如下：

Begin:

初始化种群；

for(i=1；i≤演化代数；i++)

{for(j=1;j≤种群大小;j++)

{依次处理种群的每个个体q：用算法NMEP处理个体中的每个基因；}

如果(i<演化代数)

{交叉；变异；}

}

输出最佳个体；

End

5 实验分析

由以上叙述可知，NMEP仅在评估时对MEP的基因进行了等价去重处理，并没有对演化规则、过程进行任何变动，因而嵌入NMEP的MEP与传统MEP应有一样的精度，自然无需就精度进行实验比较。

新方法采用MEP的适应值计算方法，即计算单染色体中所有基因的适应值，然后以最佳值来表征个体适应值，详见式(2)。

(2)

本节针对符号回归问题做了三个实验，其中目标函数如式(3)～式(5)所示，x,y∈[-100，100]，涉及的参数见表2，S和E分别表示sin和exp运算，比较的对象是运行时间。

z=x4+x3+x2+x

(3)

z=sin(exp(sin(exp(sin(x)))))

(4)

z=x3+x2y-y

(5)

为更好地体现新方法的时间优势(主要得益于消除基因的重复引用，即语义的重复计算现象)，还增加了演化过程的语义复杂度，如为每个基因的处理/运行额外添加了语义延时程序extra()。它的一次执行将达万次“a++”之众。

Table 2 Parameters of experiment 1～experiment 3

图2～图4为通过实验1～实验3对比嵌入NMEP的MEP与传统MEP的时间开销，图中横坐标表示运行次数，纵坐标表示时间，单位是s。每个实验都有两条曲线，位于下方的曲线(时间少)均是嵌入NMEP的MEP的演化时间；位于上方的曲线(时间多)均是传统MEP的演化时间。由图2～图4可知，传统MEP在时间性能上明显落后于嵌入NMEP的MEP，也即新评估方法拥有较大的时间优势。

Figure 2 Time comparison between NMEP-based MEP and traditional MEP in experiment 1图2 实验1中嵌入NMEP的MEP与传统MEP时间比较

Figure 3 Time comparison between NMEP-based MEP and traditional MEP in experiment 2图3 实验2中嵌入NMEP的MEP与传统MEP时间比较

Figure 4 Time comparison between NMEP-based MEP and traditional MEP in experiment 3图5 实验3中嵌入NMEP的MEP与传统MEP时间比较

图5～图7刻画三个实验中NMEP查出传统MEP演化过程包含的基因的重复次数。图中横坐标表示演化代数，纵坐标表示传统MEP的基因的重复引用次数。从图5～图7的基因的重复引用总量看来，重复量是不可小觑的。试想如果被重复计算的语义动作的时间复杂度很高，那么大量重复将耗费庞大的运算时间和其他资源。

Figure 5 Repeat number NMEP finds out in experiment 1图5 实验1中算法NMEP查找出的重复次数

Figure 6 Repeat number NMEP finds out in experiment 2图6 实验2中算法NMEP查找出的重复次数

Figure 7 Repeat number NMEP finds out in experiment 3图7 实验3中算法NMEP查找出的重复次数

综观图2～图7，当传统MEP的种群在演化过程中涉及的基因重复引用量、语义动作的运算量越大，嵌入NMEP的MEP所节省的时间就越多。由上可知，嵌入NMEP的MEP在不改变传统MEP演化规则和精度的基础上，能够准确有效地识别被重复使用的基因，避免重复计算带来的大量的资源消耗，使得MEP在性能上得到较大的提高。这表明，针对MEP的去重运算研究不仅具有充分的理论依据，而且在具体实现环节也是可行的，是拥有重要前景的一个研究领域。

6 结束语

本文首先深入分析了MEP的基因在染色体中的表示特点及采用的评估方法，发现每个染色体中的任何基因都有可能多次被当前或其它后续种群中的其他基因引用，造成重复计算的现象，继而给出了现象出现的充分条件，以及处理的理论依据和具体算法。算法NMEP在保证与传统MEP精度相同的基础上，能有效识别会被重复引用的基因，避免大量重复计算，节省了宝贵的时空资源。最后的实验结论表明，去重计值后，嵌入NMEP的MEP在性能上有显著提高。可见，去重研究对于MEP的整体研究具有重要的意义。我们下一步将用类似方法分析GEP的评估问题，相信在深度优先解码方式下会有相似效果。

[1] Koza J R.Genetic programming:On the programming of computers by means of natural selection[M]. Cambridge:MIT Press, 1992.

[2] Ferreira C.Gene expression programming:A new adaptive algorithm for solving problems[J]. Complex Systems, 2001, 13(2):87-92.

[3] Oltean M, Grosan C. A comparison of several linear genetic programming techniques[J]. Complex Systems, 2003, 14(4):285-313.

[4] McKay R I, Hoal N X, Whigham P A,et al. Grammar-based genetic programming:A survey[J]. Genetic Programming and Evolvable Machines, 2010, 11(3-4):365-396.

[5] O′Neill M, Ryan C. Grammatical evolution[M]. Dordrecht:Kluwer Academic Publishers, 2013.

[6] Oltean M, Grosan C, Diosan L,et al. Genetic programming with linear representation:A survey[J]. International Journal on Artificial Intelligence Tools, 2009, 19(2):197-239.

[7] He Pei,Kang Li-shan,Johnson C G,et al.Hoare logic-based genetic programming[J]. Science China(Information Sciences), 2011, 54(3):623-637.

[8] He Pei, Johnson C G, Wang Hou-feng. Modeling grammatical evolution by automation[J]. Science China Information Sciences, 2011, 54(12):2544-2553.

[9] Oltean M. Improving the search by encoding multiple solutions in a chromosome[M]∥Evolutionary Machine Design:Methodology and Applications,2005:88-110.

[10] Harman M. Software engineering meets evolutionary computation[J]. IEEE Computer, 2011, 44(10):31-39.

[11] Mitchell M. An introduction to genetic algorithms[J].Cambridge:MIT Press, 1996.

[12] O’Neill M, Vanneschi L, Gustafson S,et al. Open issues in genetic programming[J].Genetic Programming and Evolvable Machine, 2010, 11(3):339-363.

[13] Wu Shelly Xiaonan, Banzhaf W. The use of computational intelligence in intrusion detection systems:A review[J].Applied Soft Computing, 2010(10):1-35.

[14] Dai Mu-cheng,Tang Chang-jie,Zhu Ming-fang,et al.Automatic complex function discovery based on multi expression gene programming[J]. Journal of Sichuan University(Engineering Science Edition),2008,40(6):121-126.(in Chinese)

[15] Deng Wei,He Pei,Qian Jun-yan.Multi-gene expression programming with depth-first decoding principle[J].Pattern Recognition and Artificial Intelligence,2013,26(9):819-828.(in Chinese)

[16] Zhang Jia-wei,Wu Zhi-jian,Huang Zhang-can,et al.Classification based on multi expression programming[J]. Journal of Chinese Computer Systems,2010,31(7):1371-1374.(in Chinese)

[17] Zhao Xiu-yang, Zhang Cai-ming, Wang Ya-nan,et al. A hybrid approach based on MEP and CSP for contour registration[J].Applied Soft Computing, 2011(11):5391-5399.

[18] Mirzahosseini M R, Aghaeifar A, Alavi A H, et al. Permanent deformation analysis of asphalt mixtures using soft computing techniques[J]. Expert Systems with Applications, 2011, 38:6081-6100.

[19] Alavi A H, Gandomi A H. Energy-based numerical models for assessment of soil liquefaction[J].Geoscience Frontiers, 2012, 3(4):541-555.

[20] Alavi A H, Aminian P, Gandomi A H,et al. Genetic-based modeling of uplift capacity of suction caissons[J].Expert Systems with Applications, 2011, 38:12608-12618.

[21] Jiang Da-zhi,Peng Chen-feng,Liu Liang. Forecasting soil slope stability with MEP algorithm[J]. Journal of Shantou University(Natural Science Edition),2011,26(4):66-72.(in Chinese)

附中文参考文献：

[14] 代术成，唐常杰，朱明放,等.基于多表达式基因编程的复杂函数挖掘算法[J].四川大学学报(工程科学版)，2008，40(6)：121-126.

[15] 邓薇, 何锫, 钱俊彦. 深度优先的多基因表达式程序设计[J].模式识别与人工智能，2013,26(9):819-828.

[16] 张建伟，吴志健，黄樟灿,等.基于多表达式编程的分类算法研究[J].小型微型计算机系统，2010，31(7)：1371-1374.

[21] 姜大志，彭晨枫，刘亮. 边坡稳定性的预报MEP分类预测算法[J].汕头大学学报(自然科学版),2011，26(4)：66-72.