基于PSO 算法优化的BPNN 天然气脱CO2 膜分离过程软测量模型
2015-07-10李桂香王元麒
王 磊,李桂香,2,王元麒
(1. 海南大学 信息科学技术学院 海南省特种玻璃重点实验室,海南 海口570228;2. 广东省医疗器械研究所 广东省医用电子仪器及高分子材料制品重点实验室,广东 广州510500;3. 意大利米兰理工大学,意大利 米兰20133)
在资源短缺、能源紧张、环境日益恶化、节能减排呼声越来越高的今天,天然气作为一种清洁燃料,其开发利用已在全球受到普遍关注.我国天然气产量也逐年快速增加,一些高含碳的低品位油气田被投入开发生产.但未经处理的天然气高含CO2气体,不仅会降低天然气的热值,在使用和输送过程中还会腐蚀输送管道和设备.科学工作者在天然气的净化技术方面已作较多研究[1].目前为止,国内外分离天然气中的CO2主要有溶剂吸收法、变压吸附法和低温分离法等[2-3].其中,气体吸收法约占70%,但有其局限性,如含高浓度CO2时,能量消耗高;处理量小时费用较高;脱碳工艺流程复杂和设备尺寸过大.随着近年来膜制备方法与膜分离工艺的发展,气体膜分离法以其节能、高效、操作简单、使用方便、不产生二次污染等优点,被认为是最有发展潜力的脱碳方法之一[4-5].
天然气脱CO2膜分离过程属于气体膜分离过程,是一个包含大量信息的多变量影响、时变的非线性系统,过程中难以在线精确测量的关键性能参数直接影响其过程的实时控制.目前,其过程中最重要的性能参数脱碳气流量和尾气CO2浓度大都靠人工测量,前者受到过程中压力和温度的影响测量不准确,后者需要昂贵的、难以维护的仪器,成本太大.虽然国内外已对气体膜分离技术做了不少研究,但主要集中在膜材料和膜,而较少对组件、装置及过程优化等方面进行研究[6].实际工业应用时,复杂时变的现场条件,使得难以对其过程建立精确的数学/机理模型[7-8].为实现气体膜分离的过程优化控制,文献[7]针对炼厂气氢回收过程中一些重要性能参数难以在线测量,将软测量方法引入气体膜分离技术.文献[9]进一步引入主元分析方法,对氢回收膜分离过程RBFNN 模型建模变量进行分析并提取出关键的辅助变量进行建模,简化了建模过程.但神经网络存在容易陷入局部最小值和收敛速度慢等问题[10],且在建模时都没有对神经网络参数进行优化,可能缺乏通用性.
粒子群算法(Particle Swarm Optimization,PSO)是由KENNEDY 和EBERHART 模拟鸟群捕食行为发明的一种全新全局优化算法[11].算法中把每个优化问题的解都当作搜索空间的一个粒子.该算法具体原理是首先初始化一群随机粒子,对每个粒子赋予一个由适应度函数确定的适应值和决定其方向和距离的速度值,粒子每次迭代时通过跟踪个体极值和全局极值更新自己.
如果用PSO 算法对神经网络的权值进行训练,就能得到较快的收敛速度;如果用其优化神经网络阈值,就可让BP 神经网络避免陷入局部最小值.因此,在建立基于PSO 算法优化的BPNN 天然气脱CO2膜分离过程软测量模型时,首先用PSO 算法对BP 神经网络的权值和阈值进行优化,得到优化的软测量模型,然后再结合现场采集处理的数据用所建模型对天然气脱CO2膜分离过程性能参数进行测量研究.
1 理论基础
1.1 粒子群算法 PSO 算法源于人们研究人工智能和鸟群捕食行为,基于种群全局搜索策略,通过众多种群粒子间的合作与竞争进行优化搜索.1995 年,KENNEDY 和EBERHART 受鸟群觅食行为启发提出了PSO 算法[12].现在PSO 算法进化成了一种基于群体智能的进化计算技术,简单、容易实现,既适合科学研究,又适合工程应用[13].PSO 算法原理:
假设一个n 维搜索空间中有m 个粒子组成的一个种群X=(X1,X2,…,Xm)T.其中,Xi=(Xi1,Xi2,…,Xin)T为第i 个粒子的位置,Vi=(Vi1,Vi2,…,Vin)T为其速度,Pi=(Pi1,Pi2,…,Pin)T为个体极值,Pg=(Pg1,Pg2,…,Pgn)T为种群全局极值.找到个体极值和全局极值后,粒子分别根据下式更新速度和位置
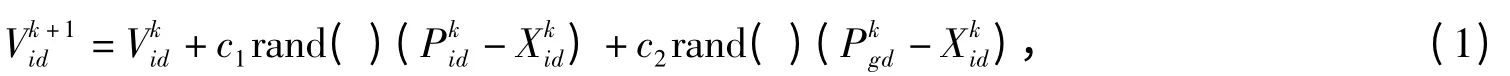

其中,c1和c2是加速因子,取非负常数;rand()是随机常数,介于(0,1)间和分别是第k 次迭代时,粒子i 的第d 维速度和位置是粒子i 的第d 维个体极值位置是群体的第d 维全局极值位置.
本文引入了惯性权重算法和收缩因子到传统PSO 算法中进行改进.使得迭代时,粒子的速度由以下公式确定
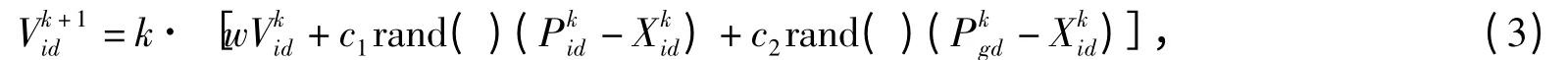
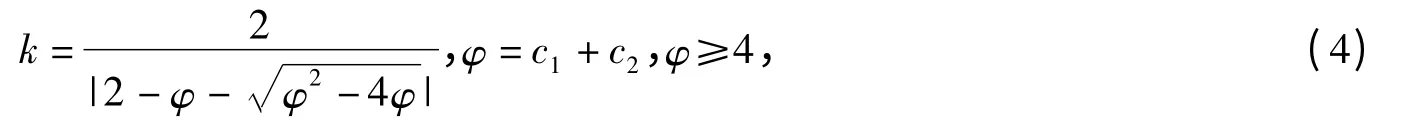
其中,w 是惯性权重函数,根据迭代次数对w 进行动态调整,使得w 随着代数的增加而减少,即搜索范围越来越小,加快收敛速度;伸缩因子k 用来控制粒子的全局速度与局部速度的平衡.
1.2 基于PSO 优化的BP 神经网络 人工神经网络是一门新兴的交叉学科,是模拟人脑智能结构和功能开发出来的非线性信息处理系统.其中的误差反向传播(Back Propagation,BP)神经网络是应用最多的,它具有良好的容错性、强大的自学习能力和非线性映射能力[14-16].但是BP 网络采用的BP 算法对初始网络的权值及其敏感,易存在陷入局部最小值和收敛速度慢等缺点.
因此,利用上述改进的PSO 算法优化神经网络的连接权值和阈值以充分发挥PSO 算法的全局寻优能力和BP 神经网络的局部搜索能力,提高神经网络模型的泛化学习能力.PSO 算法优化BP 神经网络的具体流程如图1 所示.
1.3 天然气脱CO2膜分离过程技术原理 气体膜分离是一种新型的化工分离技术,以膜两侧气体压力差为驱动力,使得CO2溶解并渗透过膜,从而使该组分在膜的原料一侧浓度降低,而在膜另一侧达到富集,达到天然气脱除CO2的目的.
天然气脱CO2膜分离系统由2 部分组成:预处理和膜分离.预处理部分主要包括:过滤和加热.原始天然气经过前置的一级过滤器和两级精密过滤器脱除颗粒及油雾,将天然气中的含重烃量降低到0.003 ppm 以下,同时滤除直径大于0.01 m 的所有固体颗粒,然后经过加热器加热到80 ~90 ℃进入道一级膜分离器中进行分离.天然气经过一级膜分离后,由于CO2容易渗透而在低压侧得到浓缩CO2(渗透气③);在高压侧得到包含CH4的尾气(非渗透气④),尾气再经冷凝器(35 ℃)回收部分高碳组分后进入二级膜分离,低压侧的浓缩CO2(渗透气⑧)放空;而将高压一侧得到主要为天然气的尾气(非渗透气⑨)并入用户的管网.其工艺流程如图2 所示.
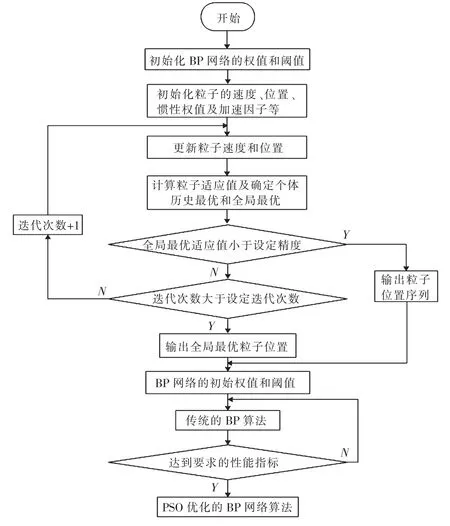
图1 PSO 优化BP 神经网络的流程
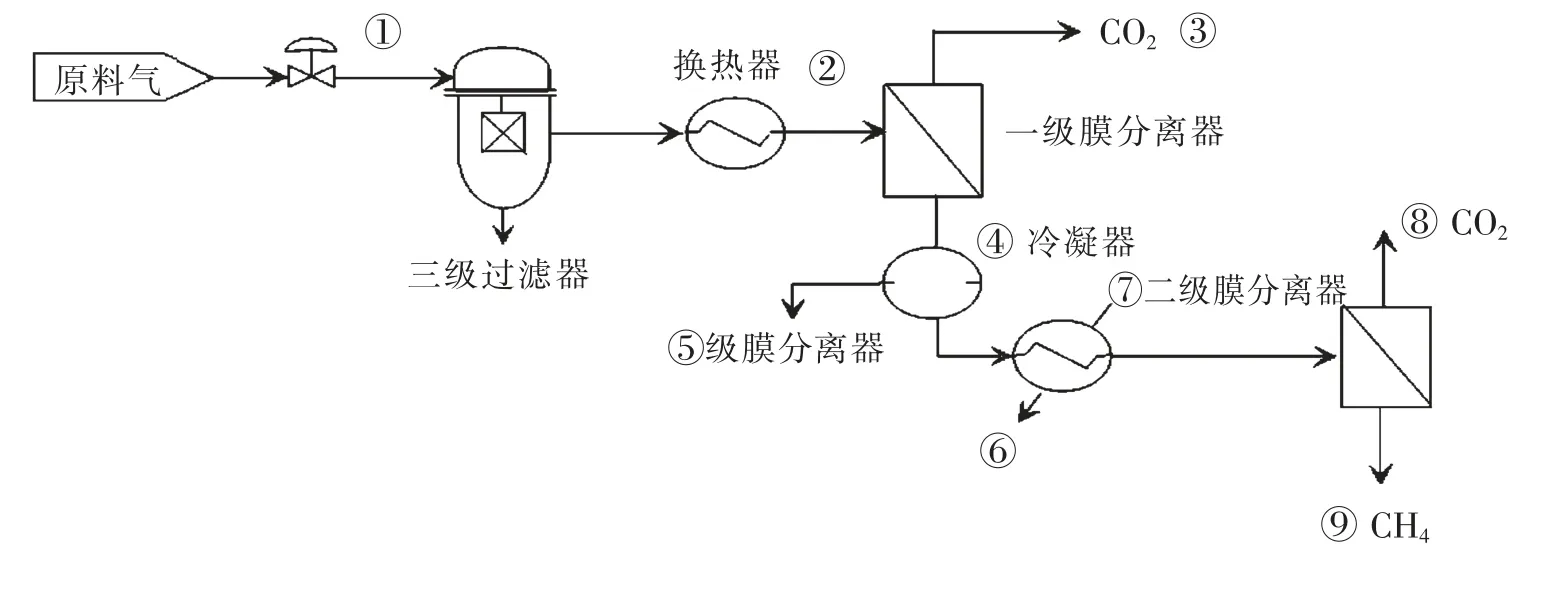
图2 天然气脱CO2 膜分离工艺流程简图
2 基于PSO 算法优化的BPNN 天然气脱CO2 膜分离过程软测量模型
建立软测量模型时选择的建模变量,需要符合气体膜分离过程机理[7].根据天然气脱CO2膜分离过程机理和现场数据,结合相互关联变量的类型、数目和测点位置以及实际应用制约的额外因素(经济性、可靠性、可行性以及维护性等)和建模输入变量需符合原则(过程适用性、灵敏性、特异性、准确性、鲁棒性等),在建立天然气脱CO2膜分离过程软测量模型时,选择其过程中主要影响上述性能的变量作为建模输入和输出,其中输入为入口温度(T)、入口压力(Pf)、渗透气压力(Pp)、尾气压力(Pr)和原料气流量(Qf)、原料气CO2浓度(Cfq);输出为关键性能指标脱碳气流量(Qp)和脱碳气CO2浓度(Cpq).
从图3 和图4 中可以看出,基于改进PSO 算法优化的天然气脱CO2膜分离过程BPNN 模型收敛,且应用模型得到的2 个过程性能参数预测值与真实值吻合较好.图5 和图6 精确地给出了基于改进PSO 算法优化的天然气CO2膜分离过程BPNN 模型的仿真误差,都在1.4%以内,完全符合实际运用.实际上,仿真时间都远小于1 s,基于改进PSO 算法优化的BPNN 所建的天然气脱CO2膜分离过程模型比用没有优化的BPNN 模型测量过程性能参数(如图7、图8 和表1)更精确. 综上所述,基于改进PSO 算法优化的BPNN 所建的天然气脱CO2膜分离过程软测量模型正确合理,可为天然气脱CO2膜分离过程的实时控制提供基础.
在采集过程数据时,理论上需要采集包含工业对象相关信息的大量过程数据用于建模和模型检验.而实际只采集软测量模型建立所需的相应输入输出变量过程数据,并且数据覆盖面尽量宽至整个操作范围,以便于拓宽软测量模型的应用范围. 同时对采集数据进行处理,以得到正确可靠的数据确保测量精度.
建模样本为海南澄迈福山油田天然气脱CO2两段膜膜分离过程装置中具有代表性的100 组预处理数据.首先样本数据用统计假设校验法剔除其中具有显著误差的数据,再用平均滤波法除去包含随机误差的数据,并且前50 组数据作为建模训练样本,后50 组数据用于校验模型的正确有效性.
基于以上描述,可以得到基于PSO 算法天然气脱CO2膜分离过程的BPNN 软测量模型为

其中,T 为入口温度,Pf为入口压力,Pp为渗透气压力,Pr为尾气压力,Qf为原料气流量,Cfq为原料气CO2浓度,Qp为脱碳气流量,Cpq为脱碳气CO2浓度.
3 仿真结果与分析
为了验证模型的正确性和有效性,借助Matlab2010a 软件平台和神经网络工具箱,编程实现了基于PSO 算法优化的BPNN 天然气脱CO2膜分离过程软测量模型,并应用数据对模型进行了训练和校验.
所建模型仿真测量的脱碳气流量和脱碳气CO2浓度2 个关键性能指标结果如图3 和图4 所示.
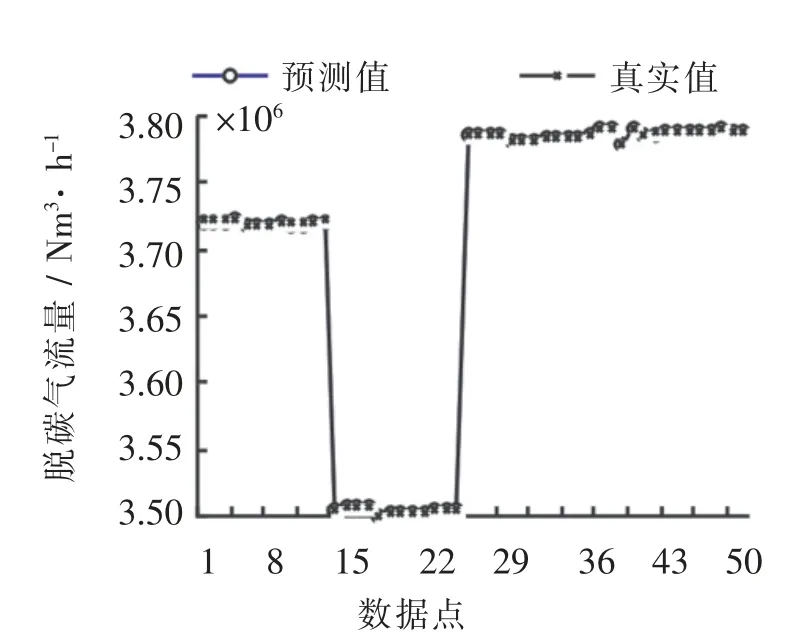
图3 脱碳气流量测量
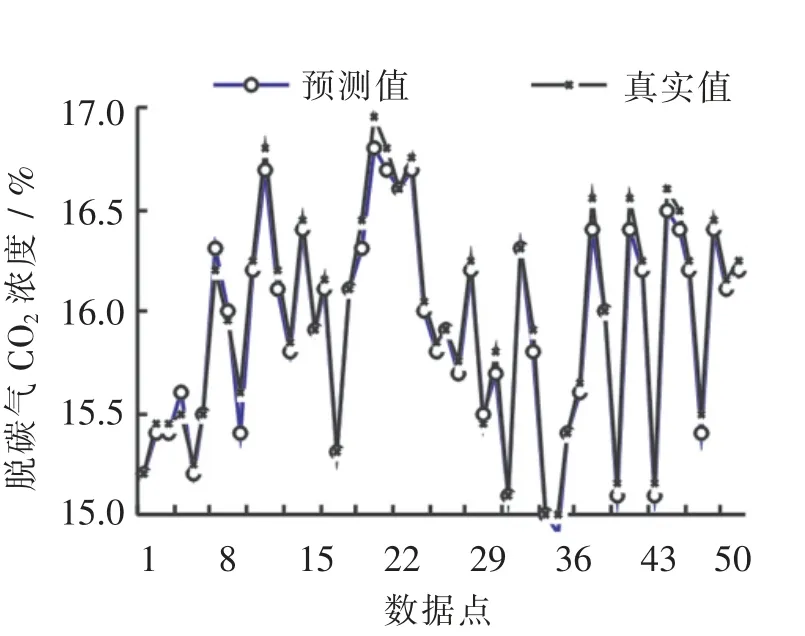
图4 脱碳气CO2 浓度测量
为了对模型的预测精确度进行评估,采用相对误差进行评价,相对误差定义式(6)对其进行评判.

其中,Y0表示模型测量输出,Y 表示实际测量值.
2 个关键指标的仿真误差分别如图5 和图6 所示.
用基于改进PSO 算法优化的BPNN 天然气脱CO2膜分离过程软测量模型与没有用PSO 算法优化的BPNN 软测量模型对天然气脱CO2膜分离过程性能参数进行测量的最大误差对比,如表1 所示.
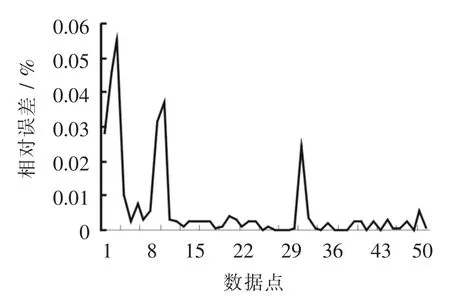
图5 脱碳气流量测量误差
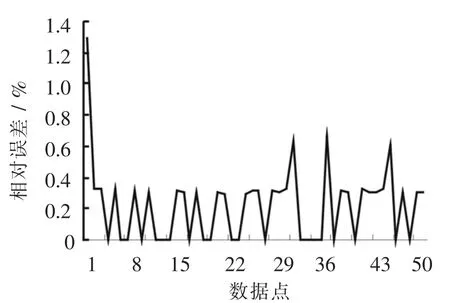
图6 脱碳气CO2 浓度测量误差
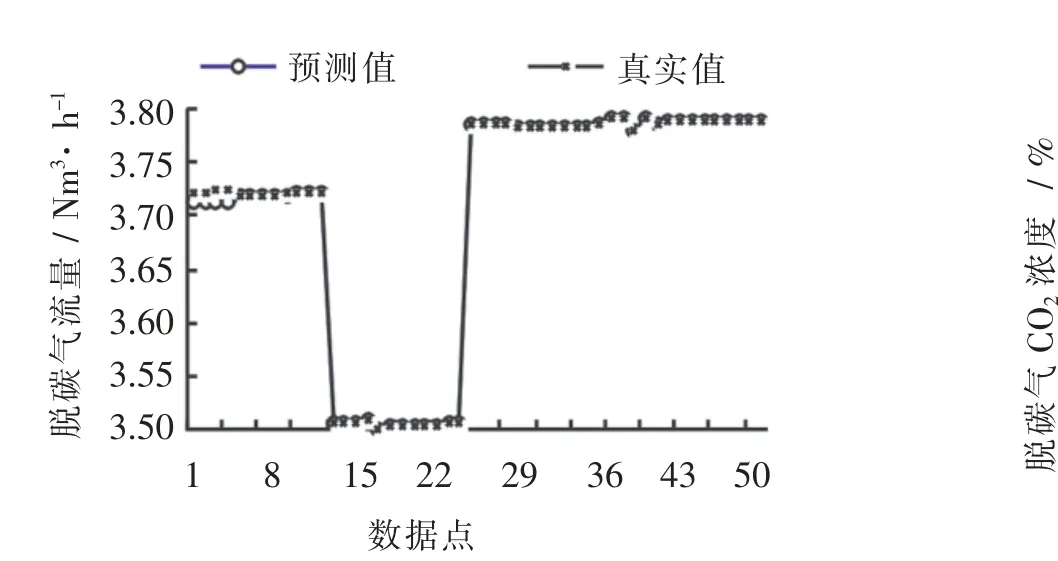
图7 BPNN 模型测量脱碳气流量
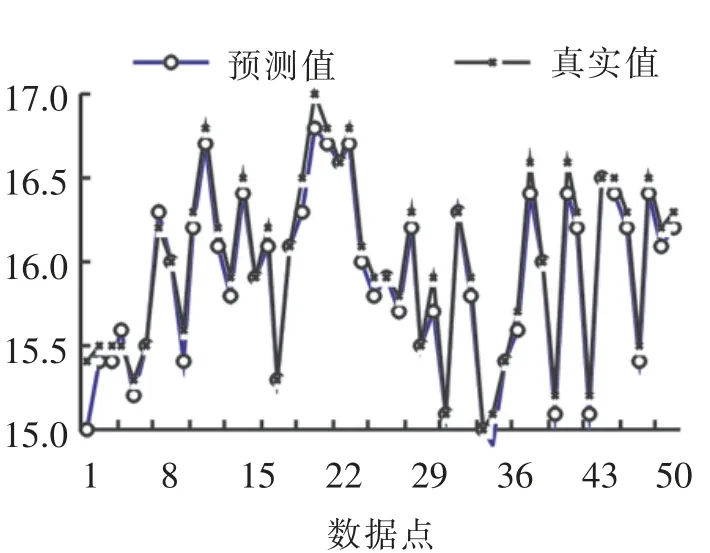
图8 BPNN 模型测量脱碳气CO2 浓度

表1 测量模型测量天然气脱CO2 膜分离过程性能参数误差对比
4 小 结
通过用改进PSO 算法对BP 神经网络进行优化,建立了基于改进PSO 算法优化的天然气脱CO2膜分离过程BPNN 软测量模型,并对天然气脱CO2膜分离过程的过程关键性能参数进行了测量.仿真结果表明,模型对天然气脱CO2膜分离过程的脱碳气流量和尾气CO2浓度的测量值同实测值基本吻合,精度高,速度快,证明了模型的合理正确性.当然,该测量模型还可以应用于其他气体的膜分离过程关键性能参数的检测,指导其过程的实时控制,具有较好的实际应用价值,并为气体膜分离关键性能参数的在线检测和过程的实时控制提供基础.
[1]黄斌,刘练波,许世森. 二氧化碳的捕获和封存技术进展[J]. 中国电力,2007,40(3):14 -17.
[2]Jose D F,Timothy F,Sean P,et al. Advances in CO2capture technology[J]. International Journal of Greenhouse Gas Control,2008,2:9 -20.
[3]丁洁,李舒宏,程德园,等. 新型CO2低温捕集与N2/O2分离复合系统性能分析[J]. 化工学报,2012,63:161 -165.
[4]汪东. 气体膜分离的原理及其应用于酸性气体净化的研究发展[J]. 化学工业与工程技术,2008,29(5):50 -52.
[5]孙翀,李洁,孙丽艳,等. 气体膜分离混合气中二氧化碳的研究进展[J]. 现代化工,2011,31(S1):19 -23.
[6]张菀乔,张雷,廖礼. 气体分离膜技术的应用[J]. 天津化工,2008,22(3):21 -22.
[7]Wang L,Shao C,Wang H,et al. Radial basis function neural networks-based modeling of the membrane separation process:hydrogen recovery from refinery gases[J]. Journal of Natural Gas Chemistry,2006,15(3):230 -234.
[8]Koros W J. Some opportunities & challenges for our membrane community to consider-with an Emphasis on gas separations[J].Membrane Science and Technology ,2006,26(4):1 -5.
[9]李桂香,王磊,李继定,等. 基于主元分析的气体膜分离过程RBFNN 建模[J]. 系统仿真学报,2012,24(9):2003-2006.
[10]Keninedy J,Eberhart R C. Particle swarm optimization:proceedings of the 1995 IEEE International Conference on Neutral Networks,Perth,November 27 -December 1,1995[C].New Jersey:IEEE Press.1995.
[11]周树孝,王文昌,王留成,等. 散式流化和聚式流化的BP 神经网络识别[J]. 高校化学工程学报,2004,18(4):459-464.
[12]刘建华,刘国买,杨荣华,等. 粒子群算法的交互性与随机性分析[J]. 自动化学报,2012,38 (9):1471 -1484.
[13]Eberhart R C,Shi Y. Particle swarm optimization developments,application and resources:proceedings of the 2001 Congress on Evolutionary Computation,Seoul,May 27 -30,2001[C].[S.1.]:IEEE Press,2001.
[14]韩力群. 人工神经网络理论、设计及应用[M]. 北京:化学工业出版社,2007.
[15]张宏建,孙志强. 现代检测技术[M]. 北京:化学工业出版社,2009:59 -68.
[16]张雨浓,杨逸文,李巍. 神经网络权值直接确定法[M]. 广州:中山大学出版社,2010.
