基于排队论模型的装配型供应链绩效分析
2015-07-09云南外事外语职业学院经济管理学院刘丽刘凯徐宴丽
云南外事外语职业学院经济管理学院 刘丽 刘凯 徐宴丽
物流商论 Logistics
基于排队论模型的装配型供应链绩效分析
云南外事外语职业学院经济管理学院 刘丽 刘凯 徐宴丽
摘要:汽车制造业的物流网络,由不同的主体构成一个动态的物流网络,各个节点靠物流信息系统所连接。上下游供应商为汽车制造企业提供所需的零部件,但可能因为某个节点的意外中断而导致整条供应链的失效。在装配型供应链中,不确定性因素和安全隐患将导致供应链的失效或瘫痪,提高供应链的健壮性至关重要。本文旨在将装配型供应链转化成近似等价的串行供应链,应用排队论方法对装配型供应链进行绩效分析,帮助供应商进行选择决策。
关键词:装配型供应链 Bernoulli排队论 绩效分析
1 引言
汽车工业从零部件供应、零件加工、整车装配到汽车分销,形成一条庞大复杂的供应链网络。对于汽车业这一类高价值、结构复杂、但又具有生产性、消费性的产品,由于客户需求的多样性和随机性,从而对生产系统的柔性、准确性要求苛刻。对于追求经济效益的企业来说,如何改善供应链的不确定性和提高其健壮性是当前务必解决的重要问题。
对于装配型供应链,学者主要研究的是如何解决供应链低效的问题,如朱宇清、胡大伟基于CPFR汽车装配型企业供应链管理模式研究;陈靖、陈怀莉、倪炎榕基于柔性组合策略的订单配置模型;李双艳装配型制造企业库存协同优化理论与方法研究;桂华明、马士华、关旭、张林兰基于supply_hub的两个供应商单制造商批量协调问题研究。
对于Bernoulli的研究,许多学者运用Bernoulli排队论解决设施选址问题,将客户分为高优先级和低优先级,用Bernoulli解决客户的排队和服务过程,给客户总数设定阀值,在阀值范围内优先服务高优先级客户。
本文的创新点在于运用基于Bernoulli服务器的排队论模型对汽车业装配型供应链销售丢失情形下的子系统的绩效分析,定量地研究了供应链健壮性,通过得出的稳态概率可以进一步研究供应链上下游供应商的不确定性对供应链稳定的影响。
2 理论基础
供应链网络中的每个阶段包括两个部分——具有一定产能的服务器和本阶段成品库存的缓冲区。服务器分为两种状态:正常和中断。正常状态时,服务器保持其产能;而中断状态时,服务器暂时失去其产能。所有阶段都采用基本存量策略作为库存策略,因此只要某阶段的库存水平低于基本存量水平,该阶段就会向其上游阶段下达订单。
2.1涉及的符号
2.1.1Bernoulli排队论供应链模型
2.1.2相关定理
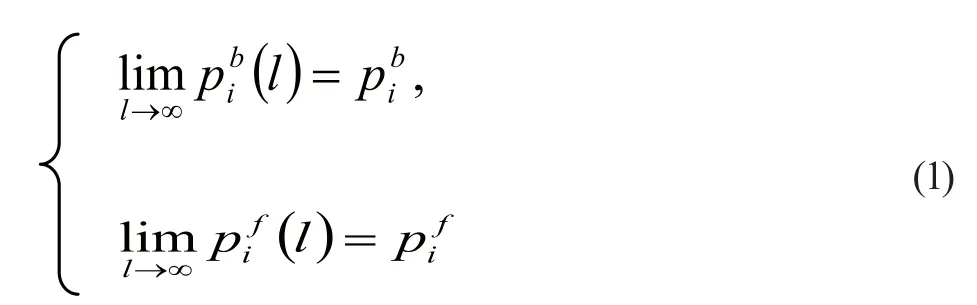
定理2,式(2)中的函数:
实验试剂及药品:新鲜牛血、柠檬酸钠、甲苯、生理盐水、20 nmol/L磷酸缓冲液、Sephadex G-75凝胶、考马斯亮蓝R250染液、脱色液、1M Tris-HCL PH6.8缓冲液、1.5M Tris-HCL PH8.8缓冲液、30%Acr-Bis(29∶1)、10%SDS、10%过硫酸铵、TEMED、蛋白质Marker、蛋白质电泳上样缓冲液、5×蛋白质电泳缓冲液。
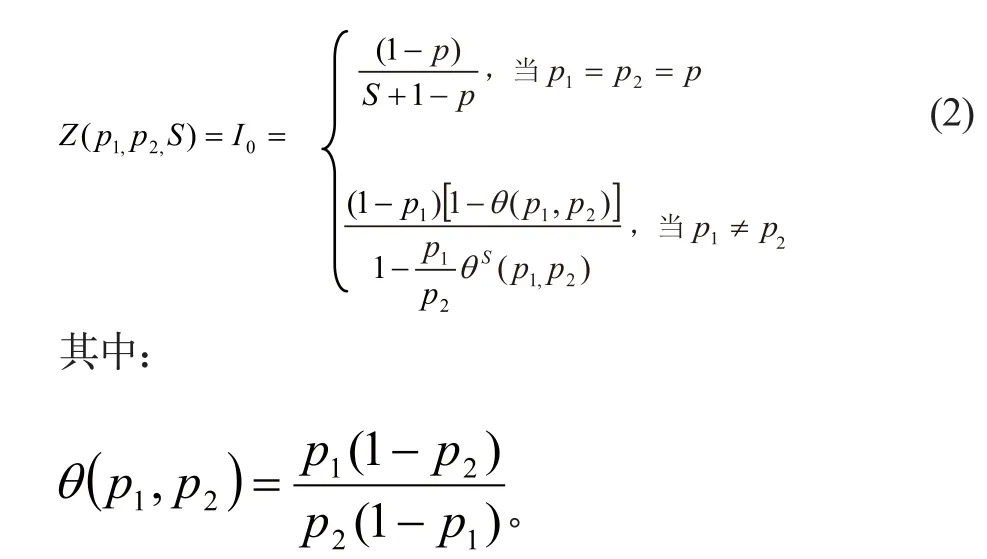
2.1.3过程详解
把装配系统转化为近似的串行供应链网络,每个串行供应链网络由一个装配子系统和部件子系统组成,除了服务器{0,1}的参数外,其他所有服务器的参数和原装配系统中的参数保持一致。
服务器{0,1}的参数可表示为
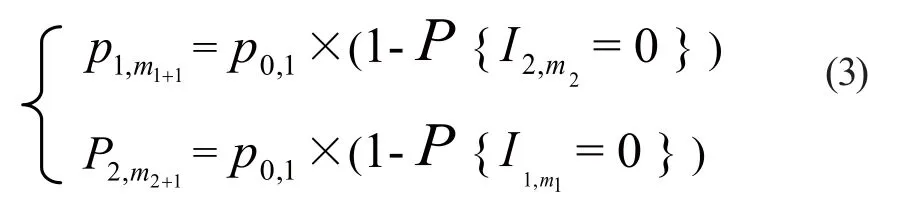
2.2主要公式
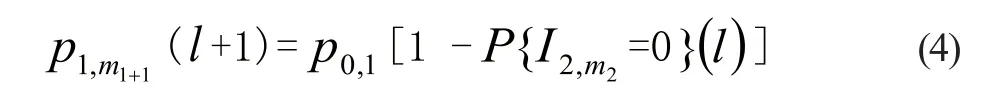
部件串行系统1的聚合公式:
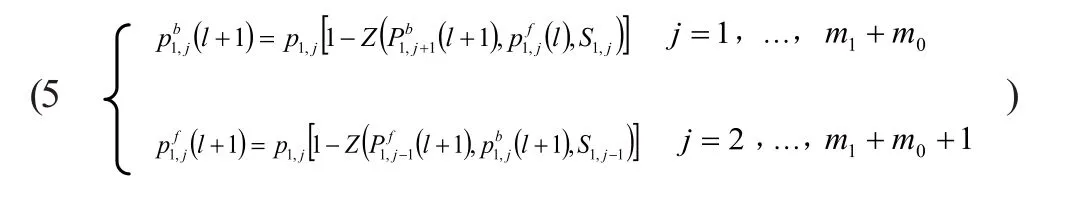
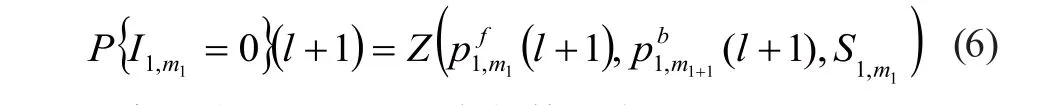
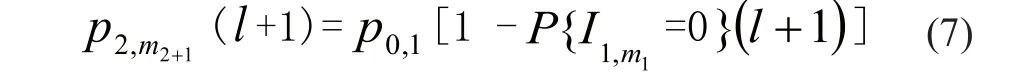
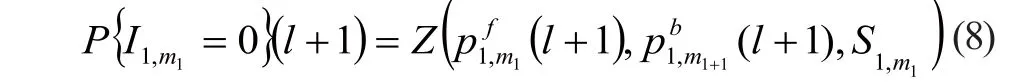
特殊值和极值如下:
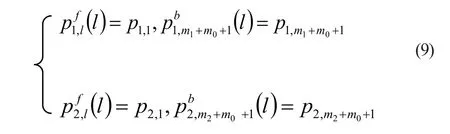
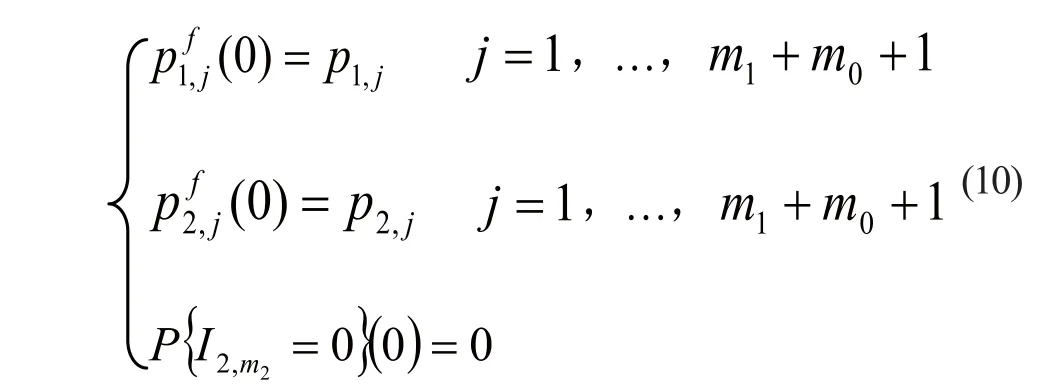
系统的生产能力。
2.2.1从顾客的角度出发
TH=P{顾客订单在单位时长期初到达}P{缓冲区非
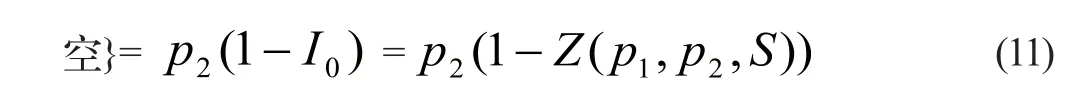
2.2.2从供应商的角度出发
TH=P{server 1 on}(1-P{缓冲区满}P{server 2
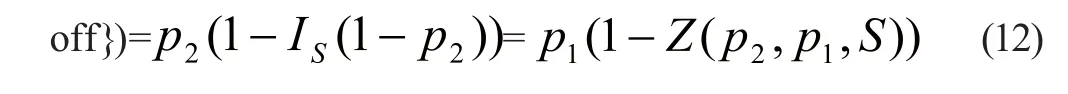
2.3迭代聚合算法的过程
(2)通过聚合公式(5)求解部件串行系统1,通过式(6)计算缓冲区{1}为空的概率。
(3)通过公式(3)的后两个等式和式(7)定义部件串行系统2中的所有参数,通过式(8)求解部件串行系统2并计算缓冲区{2,1}为空的概率,如果:
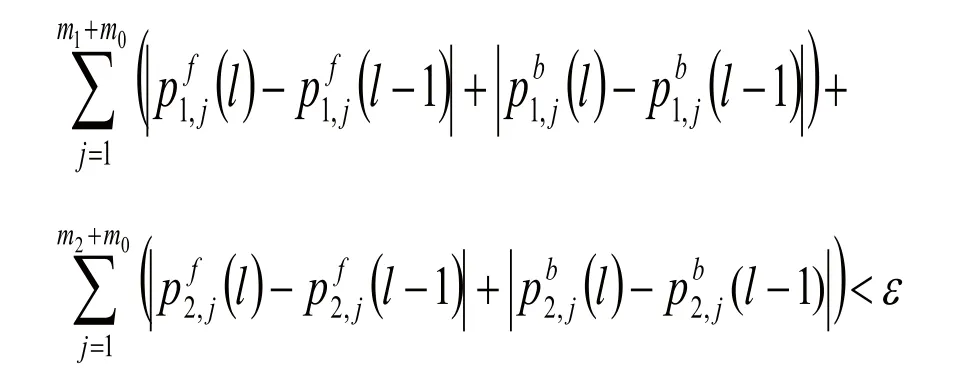
3 数值验证
迭代聚合算法的收敛性通过基于一个两部件系统的大量数值试验来说明,假设所有部件子系统和装配子系统都只包括两个阶段,每个阶段的基本存量水平设为3,订单到达率为0.9,以下数据是参考某公司内部资料得出的。
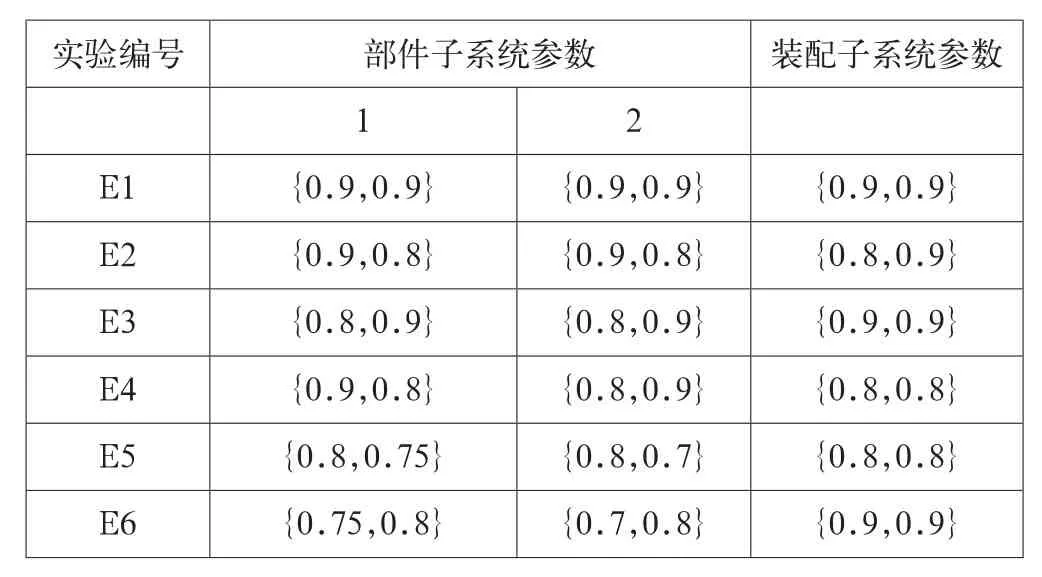
表1 数值试验参数
由图1可见算法的收敛速度之快,通常在10步迭代内就已收敛。
4 结语
供应链的稳定性对于企业的经济效益是直接联系的,供应链的不确定性对于企业的生存发展起着关键作用,如何提高供应链的健壮性是企业所需解决的问题。
本文通过将Bernoulli排队论运用到装配型两部件链系统中进行了建模,用迭代算法、前向聚合和后向聚合求出稳态概率进行了绩效分析,定量研究装配型供应链的健壮性分析,通过得出的稳态概率可以进一步研究供应链上下游供应商的不确定性对供应链稳定的影响,从而得出改善某一环节的稳定性来大大提高供应链整个网络的健壮性,提高效率降低成本。然而本文未讨论多部件链销售丢失情形的情况,也没有进一步将迭代算法用于不稳定环境下供应链网络设计问题的研究。
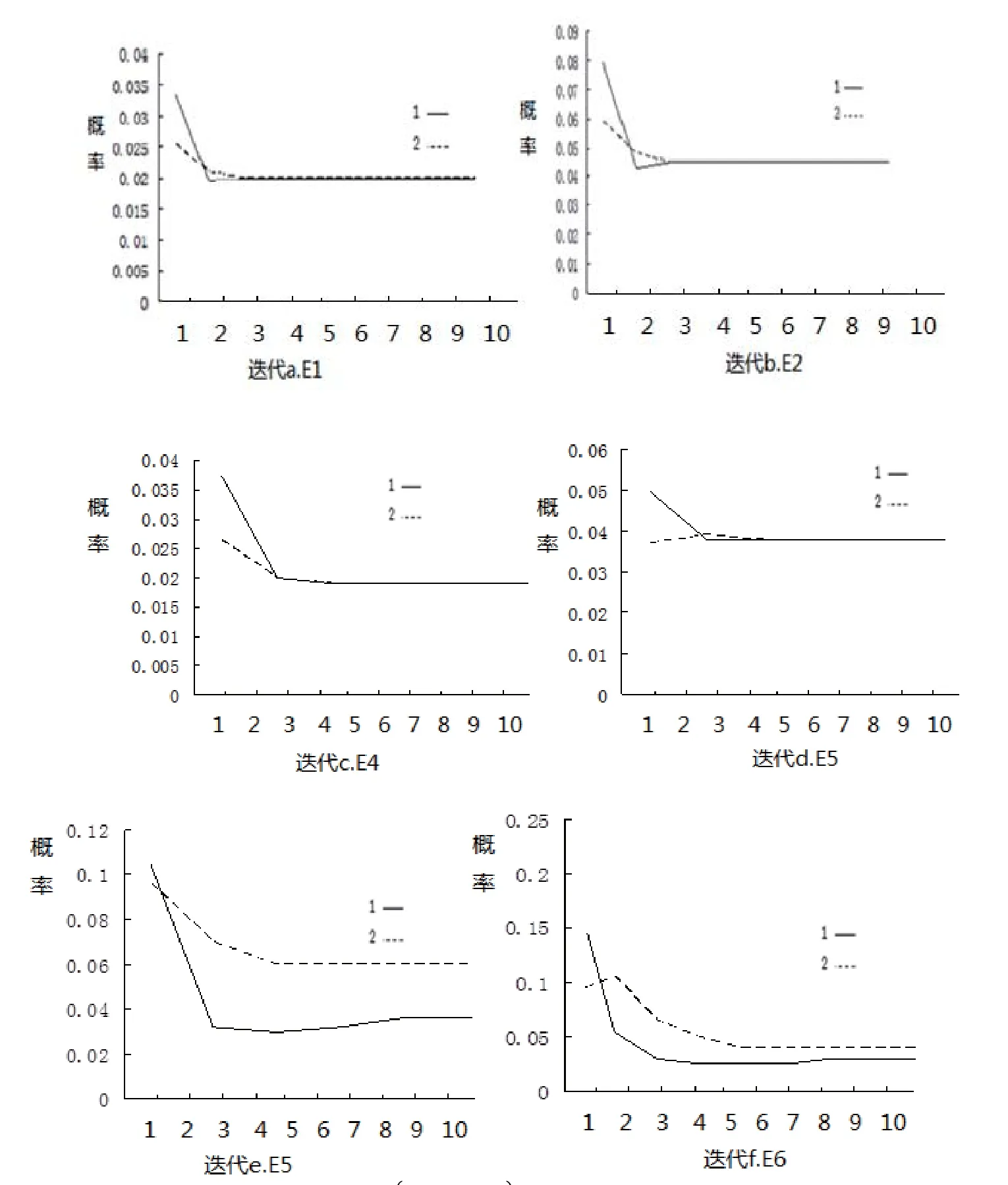
图1 概率收敛的说明
参考文献
[1]朱宇清,胡大伟.基于CPFR汽车装配型企业供应链管理模式研究[J].物流工程与管理,2012(01).
[2]陈靖,陈怀莉,倪炎榕.基于柔性组合策略的订单配置模型[J].工业工程与管理,2011(05).
[3]李双艳.装配型制造企业库存协同优化理论与方法研究[D].中南大学,2012.
[4]桂华明,马士华,关旭,张林兰.基于supply_hub的两个供应商单制造商批量协调问题研究[J].管理学报, 2012(08).
[5]洑建红.供应链健壮性评价方法[J].物流技术,2012 (21).
[6]吴书芳.汽车制造业核心型供应链风险管理研究[D].江南大学,2012.
中图分类号:F252.24
文献标识码:A
文章编号:2096-0298(2015)09(c)-083-04
