一类单控制方向已知的随机不确定二阶系统反演控制研究

晋玉强，李泽雪，雷军委

（海军航空工程学院，山东烟台， 264001）

0 引言

二阶系统具有丰富的动态特性，许多复杂的工程对象如导弹、飞机、火箭等航天飞行器在设计初期，均可以简化为二阶线性模型来设计。因此针对二阶线性系统的研究是非常有意义的。尤其是针对一组随机的二阶系统，或者针对随机的二阶系统全体的控制鲁棒性研究，是非常具有理论与应用价值的［1-5］。

在许多的工程实践中，由于外部环境变化、器件老化磨损等原因造成被控系统参数的变化，导致设计与实际存在一定误差，当对象的数学模型参数在小范围内变化时，可用一般的反馈控制、最优控制或补偿控制等方法来消除或减小参数变化对控制品质的有害影响。当控制对象的参数在大范围变化时，上面这些方法就不能圆满解决问题了［6-8］。

反演设计方法是一种反馈控制方法，它从系统的第一个状态子系统开始设计，基于Lyarpunov稳定性理论“一步一步”地反推控制律，直到完成整个控制律的设计。反演控制方法因其独特的构造性设计过程，可以有效解决模型参数未知这一问题，并且使被控系统获得较好的鲁棒性［9-11］。

本文针对简单的二阶系统，采用反演控制方法进行控制系统设计，通过与传统PID控制方法对比，从而检验反演控制是否具有良好的控制效果。最后，通过设置模型参数与给定区间完全随机选取，进行详细的随机仿真分析，通过全区间的随机遍历性的多次仿真结果，表明反演控制方法具有良好的普适稳定性和鲁棒性。

1 问题描述

具有单控制方向的二阶系统是所有二阶系统中比较简单的一种特殊情况。所谓控制方向是指模型的输入量u的系数，也称控制系数。其模型如下所示

模型的参数完全未知，且A为随机定常矩阵。反演自适应控制的目标为设计反演自适应控制器，使得系统状态x1跟踪期望值xd1。

2 PID控制律设计

图1所示为PID控制系统的结构图，该系统由PID控制器和被控对象两部分组成，PID控制器产生的控制信号对被控对象进行控制。其中PID控制器由比例 （P）、积分 （I）和微分 （D）三个环节组成。r（t）表示输入量，y（t）表示输出量，e（t）表示r（t）与y（t）的偏差。

图1 PID控制系统结构图Fig.1 Structure of PID control system

PID控制器是一种线性控制器，它根据给定期望值xd1与实际输出值x1构成控制偏差

PID的控制规律如式 （3）所示。

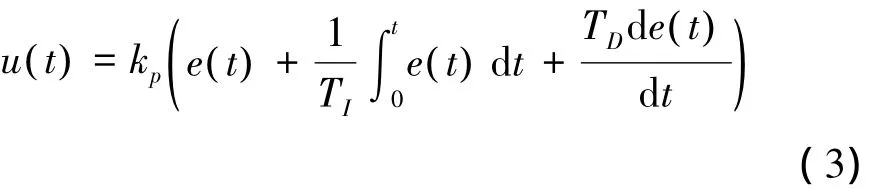
写成传递函数的形式

式中:kp为比例系数;TI为积分时间常数;TD为微分时间常数。

3 反演自适应控制律设计

针对被控系统的第一阶子系统

4 仿真分析

由于二阶线性被控系统模型参数未知，参数矩阵A的取值不能确定。参数矩阵A的不同取值也代表着不同的二阶线性被控系统，为了简化说明，并且不失一般性，本文选用期望xd1=1并对参数矩阵A在 （－10～10）的范围内随机赋值的方式进行仿真分析，观察控制效果。

4.1 PID控制仿真结果

对参数矩阵A在 （－10～10）范围内随机赋值，参数矩阵A的赋值情况如下:

a11=8.7;a12=－3.6;a21=－9.3;a22=7

针对上述赋值结果设计PID控制参数，选取PID控制参数kp=－10，ki=－5，kd=－1，得到仿真结果如图2。

图2 PID控制仿真结果图Fig.2 Simulation result of PID control

继续采用上述PID控制参数，将参数矩阵A重新随机赋值6次得到如图3～图8所示的仿真结果。

仿真结果表明，在被控系统参数取不同值时，PID控制不能有效地保证系统稳定。

4.2 反演控制仿真结果

由于k1，k3取值要足够大才能保证系统的稳定，选取反演控制参数。

k1=30，k2=1，k3=30，k4=1，k5=40，k6=40。依然采用PID仿真时参数矩阵A的赋值方法，得到如图9～图14所示的仿真结果。

图3 PID第一次仿真结果图Fig.3 The first simulation result of PID

图6 PID第四次仿真结果图Fig.6 The fourth simulation result of PID

图4 PID第二次仿真结果图Fig.4 The second simulation result of PID

图7 PID第五次仿真结果图Fig.7 The fifth simulation result of PID

图5 PID第三次仿真结果图Fig.5 The third simulation result of PID

图8 PID第六次仿真结果图Fig.8 The sixth simulation result of PID

图9 反演控制第一次仿真结果图Fig.9 The simulation result of backstepping control（the 1st）

图10 反演控制第二次仿真结果图Fig.10 The simulation result of backstepping control（the 2nd）

图11 反演控制第三次仿真结果图Fig.11 The simulation result of backstepping control（the 3rd）

图12 反演控制第四次仿真结果图Fig.12 The simulation result of backstepping control（the 4th）

图13 反演控制第五次仿真结果图Fig.13 The simulation result of backstepping control（the 5th）

图14 反演控制第六次仿真结果图Fig.14 The simulation result of backstepping control（the 6th）

仿真结果表明，反演控制可以在不同被控参数取值的情况下，都能保证系统的稳定，具有不错的控制效果。

4.3 对比与分析

通过上述仿真结果发现，由于PID控制参数是针对某一参数矩阵A设计的，当参数矩阵A发生变化时，原来设计的PID控制参数就有可能不能适应新的参数矩阵A，从而不能控制系统达到设定的期望值。反演控制参数设计时，针对于整个系统，并没有针对于某一特定的参数矩阵A设计，所以当参数矩阵A发生变化时，依然可以适应新的参数矩阵A，控制系统达到预期的控制效果。

5 结束语

在被控对象为已知单控制方向二阶线性系统时，采用传统的PID控制方法需要知道被控系统的标称数学模型，这样设计的PID控制系统可以较好地实现控制目标。但是在二阶模型参数未知的情况下，尤其是参数完全随机非均匀分布情况下，标称数学模型无法较好地定义，采用PID控制效果并不能保证所有情况均有理想的控制性能。然而采用反演法控制时，可以在并不精确地知道二阶系统模型参数的情况下，依然获得不错的控制效果，使系统具有较好的鲁棒性。在工程实践中，由于种种原因可能不能得到准确的被控模型参数，被控模型参数由于外部因素也可能发生变化，由此采用反演法设计的控制系统在模型参数完全随机分布的情况下，会有较好的应用前景。

值得补充说明的是，本文的模型参数完全随机分布，是指在某一给定区间内，符合某种概率函数分布规律来设置、选取模型参数。显然在无穷大的区间设置模型参数，讨论普遍适用的控制器设计与参数选取方法是没有意义的。

［1］胡云安，晋玉强，李海燕．非线性系统鲁棒自适应反演控制［M］．北京:电子工业出版社，2010，2（5）:35-39．

［2］X Ye，J Jiang．Adaptive nonlinear design without a priori knowledge of control directions ［J］．Automatic Control IEEE Transactions on，1998，43（11）:1617-1621．

［3］X Ye．Asymptotic regulation of time-varying uncertain nonlinear systems with unknown control directions ［J］．Automatica，1999，35（5）:929-935．

［4］X Ye．Semiglobal output feedback control of uncertain nonlinear systems with unknown high frequency gain sign ［J］．Automatic Control，IEEE Transcations on，2000，45（12）:2402-2405．

［5］X Ye．Adaptive nonlinear output-feedback control with unknown high-frequency gain sign ［J］．Automatic，Control，IEEE Transactions on，2001，46（1）:112-115．

［6］P Kokotovic．Constructive nonlinear control［C］//．Progress in the 90’S in Proceedings of IFAC 14nd World Congress．Beijing，1999，14（3）:23-25．

［7］A Saberi，EK，S Hussmann．Global stabilization of partially linear composite systems ［J］．Journal of Control Optimization，1990，28:1491-1503．

［8］Richard A，Hull D S，Zhihua Qu．Esign and evaluation of robust nonlinear missile autopilots from a performance perspective［C］//．In Proceeding of the American Control Conferences，Washington，1995，6（2）:34-38．

［9］Krstic M，Kanellakopoulos I，Kokotovic P．Nonlinear and Adaptive Control Design［M］．New York:Wiley-Interscience Publication，1995，4（3）:22-25．

［10］Swaroop D，Gerdes J C，Hedrick J K．Dynamic surface control of nonlinear systems［C］//．Proceedings of the American Control Conference，Albuquerque New Mexico，1997，2（5）:42-46．

［11］李俊，徐德明．非匹配不确定非线性系统的自适应反演滑模控制 ［J］．控制与决策，1999，14（1），46-50．