一种基于实时再处理技术的SINS初始对准算法

邓继权，马小艳，张吉先，薛 凯

（1.北京自动化控制设备研究所，北京 100074;2.北京空天技术研究所，北京 100074）

0 引言

初始对准是惯导系统进入导航的前提，也是惯导系统的关键技术之一。初始对准的两个重要指标是精确性和快速性，但是在自对准中这两者之间往往是相互矛盾的［1］。传统初始对准方法如果要在其他条件不变的情况下提高对准精度，只能通过延长初始对准时间来实现。而通常情况下，惯导系统初始对准时间都有严格限制，不可能无限延长，因此，如何在特定的初始对准时间下提高系统初始对准精度是个很大的难题。

可以将SINS中陀螺仪和加速度计的采样数据当作一组时间序列看待，通常意义下的导航解算是对该序列按时间先后顺序进行实时处理，而不必进行数据存储，就能够获得实时导航结果。如果导航计算机存储容量足够大，能够把IMU以及外部参考信息采样数据存储下来，那么既然可以按时间顺序正向处理，很容易联想到，也可以对它作逆向分析和处理。对存储的数据作正向和逆向的反复分析，有可能提高精度，或者在某项任务中能够减小实际用于分析的数据长度，即缩短任务时间［2-3］。文献［5］利用对准过程存储的数据进行多次Kalman滤波迭代计算以提高初始对准精度。本文提出一种优化的基于实时再处理技术的初始对准方法，在初始对准的不同阶段均利用相同的数据，进行多次正向、逆向处理，有利于实现惯导系统短时间高精度初始对准。

1 基于实时再处理技术的初始对准算法

1.1 初始对准算法分析

为了能够存储整个初始对准以及导航过程中的IMU数据并且实现实时再处理技术，整套惯导系统采用了两个独立的导航计算机以及大容量的存储器。其中导航计算机主板 （CPU1）用于实时的正向导航解算，在预定的对准结束时刻立即转入实时导航。导航计算机副板 （CPU2）实时存储对准以及导航过程中的IMU数据，并且在CPU1初始对准结束时刻利用其导航结果以及存储的数据进行双向导航、双向滤波实时再处理计算，由于计算机的运算速率远大于传感器的采样率，所以，经过一段时间延迟（T）之后，CPU2计算得到的导航结果也就是实时导航的结果［4-5］。其基本结构如图1所示，具体步骤如下:

1）系统通电，CPU1先进入粗对准阶段，粗对准结束后，进入Kalman滤波精对准阶段。CPU2将整个对准时间内 （设从t0时刻开始到te时刻结束）的陀螺仪、加速度计以及外部参考信息的采样数据存储下来。

2）CPU1卡尔曼滤波精对准结束后，对姿态角、陀螺漂移以及加速度计零偏等相关量进行修正。修正结束后，转入实时导航阶段。CPU2继续实时存储陀螺仪、加速度计以及外部参考信息的采样数据，同时以te时刻CPU1的速度、位置、姿态以及陀螺漂移、加速度计零偏等信息作为初值，进行基于逆向导航算法的逆向Kalman滤波估计，其中逆向陀螺漂移须将CPU1卡尔曼滤波精对准估计得到的值取反。

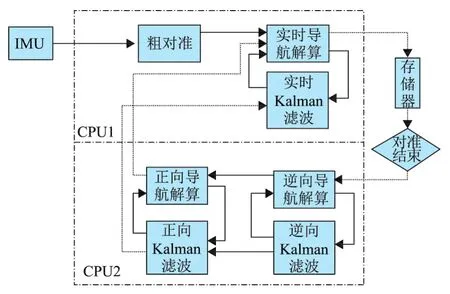
图1 基于实时再处理技术的初始对准原理图Fig.1 The initial alignment algorithm based on realtime-reprocessing

3）CPU2逆向Kalman滤波至t0时刻后，逆向Kalman滤波结束，继续以t0时刻数据作为初始值进行正向Kalman滤波估计。逆向滤波估计结束后，并不进行任何修正，直接将逆向滤波结束时刻的状态估计值conv_x^k以及估计均方误差阵conv_Pk作为正向滤波估计的初始状态估计值和初始均方误差阵，状态估计值中速度以及陀螺漂移对应项同样取反。初始速度、位置、姿态信息取逆向估计结束时刻的值。

4）CPU2正向滤波估计至te时刻后，CPU2正向Kalman滤波精对准计算结束，对姿态角、陀螺漂移以及加速度计零偏等相关量进行修正，修正结束后转入导航阶段。CPU2导航初始一段时间内所用的数据仍然是存储的数据，由于计算机运算速率远大于传感器的采样频率，经历一段时间延迟T之后，CPU2导航运算所用的数据将是实时采样的数据。因此，CPU2导航解算得到的结果也将是实时导航的结果，并且精度要高于CPU1导航解算得到的结果。用精度更高的CPU2导航结果对CPU1导航结果进行修正，提高了系统实时导航的定位精度。CPU2实时再处理对准运算结束，CPU1继续进行实时定位导航。

由上述分析可以看出，CPU2的导航运算并没有粗对准计算，CPU2通过实时再处理技术对整个初始对准过程中的数据都进行了再次处理，提高了数据的利用率。此外，CPU2逆向Kalman滤波结束后并不做任何修正，使得CPU2一次实时再处理Kalman滤波精对准计算的时间要长于CPU1初始对准时间，可以有效提高CPU2实时再处理Kalman滤波估计的稳定性。其中，延迟时间T主要取决于导航计算机副板 （CPU2）的运算能力。

1.2 卡尔曼滤波模型的建立

1.2.1 正向Kalman滤波计算

文中选取“北－天－东”地理坐标系为导航坐标系 （OnXnYnZn），原点与载体系原点重合，Xn轴指北，Yn轴指天，Zn轴指东。XnYnZn构成右手坐标系。载体坐标系（ObXbYbZb）原点位于载体重心，Xb轴沿载体纵轴向前，Yb轴垂直载体纵轴向上，Zb轴按右手坐标系。

（1）状态方程

由于捷联惯性导航系统的初始对准时间较短，因此陀螺漂移和加速度计零偏均可看成随机常数过程。另外，由于捷联惯性导航系统的高度通道是不稳定的，所以忽略垂直方向的速度以及高度，最终选取系统的状态变量XF=［δVNδVEφNφUφE δφ δλ εxεyεz∇x∇y∇z］T（由于后文将涉及正向及逆向两个状态的滤波，这里的上标F代表正向Kalman滤波，以作区别。），δVN、δVE分别为系统在导航坐标系下北向、东向速度误差;φN、φU、φE分别为导航系统的北向、天向、东向失准角;δφ、δλ分别为系统的纬度、经度误差;εbx、εby、εbz和∇b x、 ∇by、∇bz分别为载体系各轴向的陀螺漂移和加速度计零偏。

根据Kalman滤波状态方程

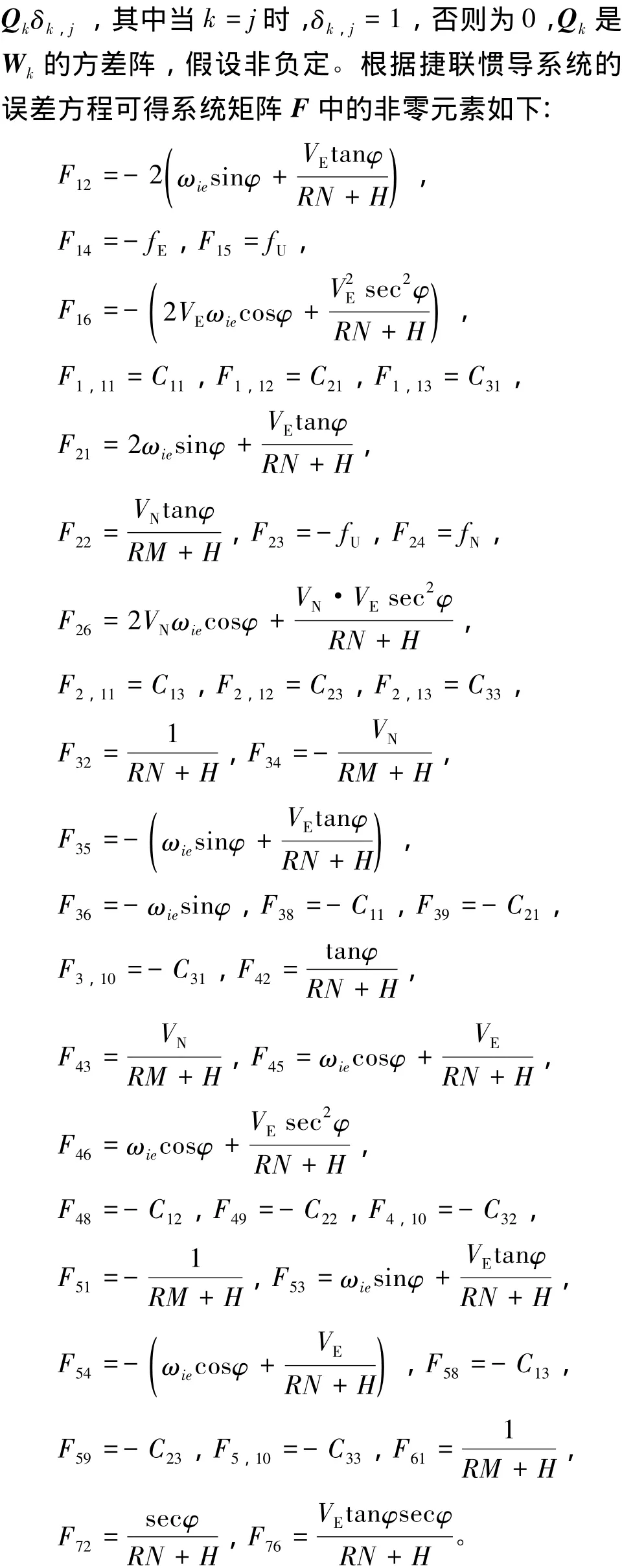
式中，Cij（i=1，2，3;j=1，2，3）为姿态转换矩阵Cbn中相应的元素。

（2）量测方程

惯导系统在Kalman滤波精对准过程中采用零速匹配方式，设tk时刻的量测值为Zk，则量测方程可表示为式 （3）。

（3）滤波计算

Kalman滤波是由 R．E．Kalman于 1960年首次提出。目前，Kalman滤波理论作为一种最重要的最优估计理论被广泛应用于各种领域，组合导航系统的设计是其成功应用中的一个最主要方面。文献［8］对Kalman滤波作了详细直观的推导，这里直接给出离散型正向Kalman滤波的基本方程:

状态一步预测

在开始滤波之前需选择合适的状态初始值XF0（一般选择零向量作为状态初始值）、估计均方误差初始值PF0以及系统噪声的初始方差阵Q0，并根据实际系统和应用环境确定适当的量测噪声方差阵Rk。参数设置完成之后，即可按照上述滤波方程递推计算系统的状态估计值。

1.2.2 逆向Kalman滤波计算

对正向捷联惯性导航算法稍作变化可以得到逆向捷联惯性导航算法［6］，由分析可以得到，只要将正向算法中的陀螺采样和地球自转角速率符号取反，并将正向结束时刻的位置、速度以及姿态信息作为逆向导航算法的初始信息，对采样数据作逆向处理，即可实现从终点至初始点的逆向导航解算。其中，逆向初始时刻速度须将正向结束时刻的速度值取反。因此，将正向卡尔曼滤波模型中的地球自转角速率和速度项取反即可得到逆向卡尔曼滤波模型。

记上标“B”表示逆向组合导航过程，则逆向组合导航的系统状态方程为

参照正向Kalman滤波计算，选择合适的反向状态初始值XB0、反向估计均方误差初始值PB0、系统噪声的初始方差阵Q0及测量噪声方差阵R0。直接可得逆向Kalman滤波计算过程如下:

状态一步预测

2 数学仿真与分析

为了能够有效的将陀螺漂移以及加速度计零偏估计出来，在仿真过程中，采用双位置Kalman滤波精对准方法。为了验证该技术的可行性，不妨假设导航计算机副板 （CPU2）的运算能力无限大，即延迟时间T等于零。具体仿真结果如图2～图4所示。对于实际系统可根据需要进行多次正、逆向迭代计算，迭代次数越多，延迟时间T越长。

具体仿真条件设置如下:

1）运载体初始纬度 φ=39.8°， 经度 λ=116.2°，高度h=80m，初始航向角ψ=－90°，俯仰角θ=0°，滚动角γ=0°。

图2 航向角误差Fig.2 Heading error

图3 水平陀螺漂移估计Fig.3 Kalman filter results of gyro-drift

2）设陀螺常值漂移为0.02（°）/h，加速度计常值零偏为100μg。

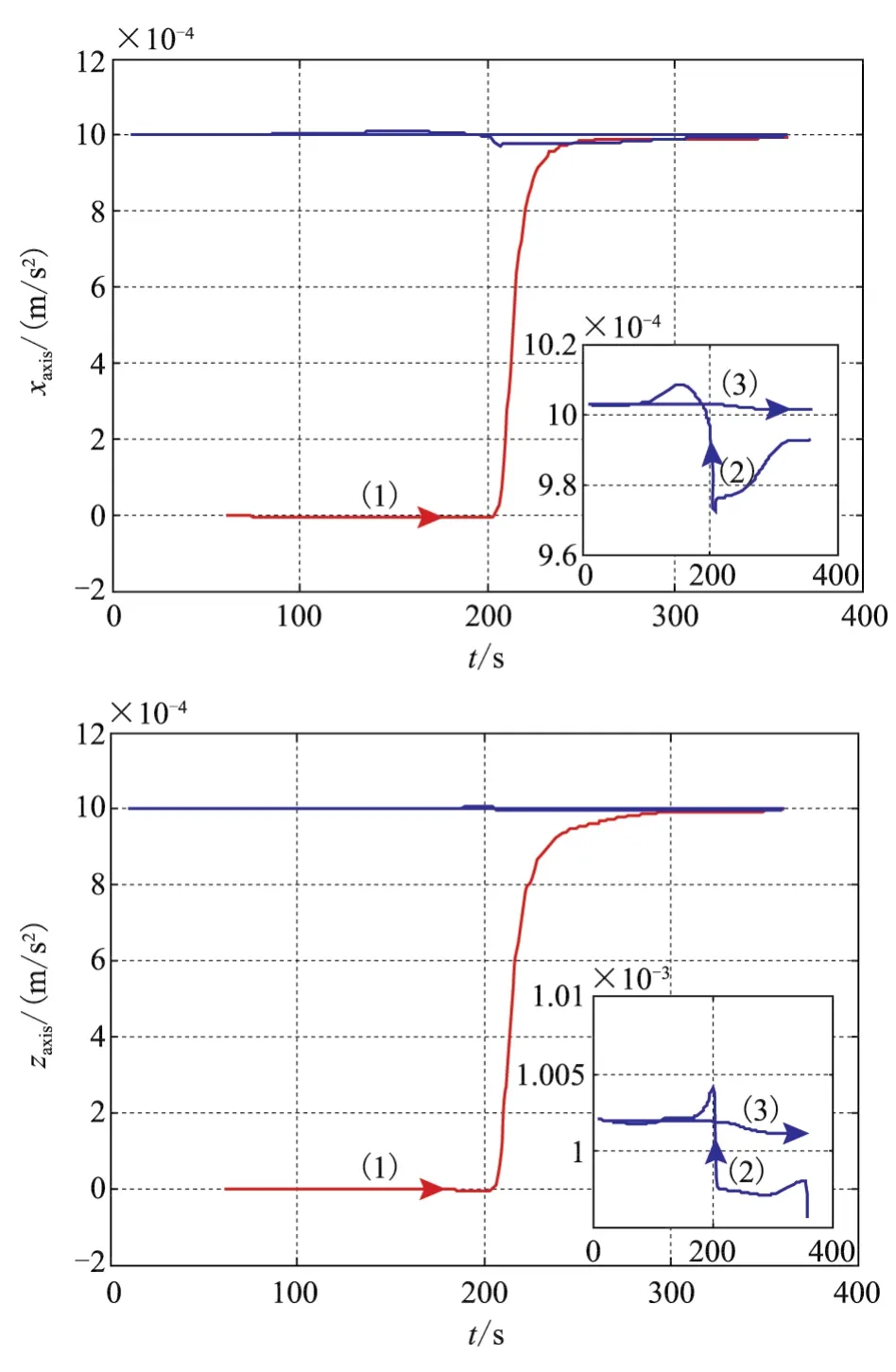
图4 水平加速度计零位估计Fig.4 Kalman filter results of accelerator-bias

3）设初始对准时间为6min，前10s为系统准备时间，粗对准时间设为50s，精对准阶段采用双位置卡尔曼滤波精对准，在200s时通过航向角转动90°引入第二位置，360s时对准结束，转位时间设为10s。

在图2～图4中，曲线 （1）表示CPU1正向Kalman滤波精对准估计结果，相当于传统Kalman滤波对准方法。曲线 （2）表示CPU2逆向Kalman滤波估计结果，曲线 （3）表示CPU2正向Kalman滤波估计结果。

为了更加直观地体现出CPU2实时再处理技术对系统初始对准精度的改善，表1给出了CPU1对准结束时刻与CPU2实时再处理对准结束时刻的姿态角误差以及陀螺漂移、加速度计零位估计结果比较。

表1 CPU1初始对准结果与CPU2实时再处理对准结果比较Tab.1 The comparison of CPU2 realtime-reprocessing result and CPU1 normal initial alignment result

从仿真结果可以看出，粗对准结束时刻，航向角误差约为5.67'，经过CPU1 Kalman精对准滤波之后，航向角误差收敛到2.21'左右。而CPU2通过实时再处理技术使航向角误差收敛到0.1'左右，使航向角更加接近于真实值。从滚动角和俯仰角也可以得到类似的结论，但是由于Kalman滤波水平失准角收敛速度较快，CPU2实时再处理后对滚动角和俯仰角精度的改善非常有限 （0.01'以内）。此外，由于CPU1 Kalman滤波时间较短，导致陀螺漂移、加速度计零位估计不够准确，而CPU2通过实时再处理技术在CPU1滤波的基础上，通过双向导航、双向滤波对陀螺漂移以及加速度计零位进行再次估计，提高了估计精度。

3 实验验证

为了进一步验证上述算法的有效性，应用此对准方法对该光纤陀螺惯导系统进行了车载实验验证。该惯导系统采用6min双位置初始对准，CPU2进行三次逆向、正向滤波实时再处理计算。在车载试验中接入GPS信息作为惯导系统纯惯性导航的基准。为了直观地体现基于实时再处理技术初始对准算法的有效性，将试验采集到的数据用常规对准方法进行仿真，比较两种情况下系统纯惯性导航1h的定位误差。

从车载试验结果可以得到，采用基于实时再处理技术的初始对准方法后，系统纯惯性导航1h的最大定位误差由3.93nmile减少到1.79nmile，有效地提高了系统纯惯性导航定位精度。车载试验结果进一步验证了文中提出的初始对准算法的有效性及可行性。

图5 水平速度误差Fig.5 Velocity error

图6 定位误差Fig.6 Position error

4 结论

本文提出了一种优化的基于实时再处理技术的捷联惯导系统初始对准方法，该方法基于双CPU捷联惯导系统，将双向导航、双向滤波相结合，实现了惯导系统的短时间高精度对准。与传统对准方法相比，该方法可以在较短的时间内取得同等的精度，或者在相同的对准时间内取得更高的对准精度。最后，通过车载试验进行了验证，具有一定的工程实用性。

［1］万德钧，房建成．惯性导航初始对准［M］．南京:东南大学出版社，1998．

［2］秦永元．惯性导航［M］．北京:科学出版社，2006．

［3］严恭敏．捷联惯导系统动基座初始对准及其他相关问题研究［D］．西北工业大学博士后研究工作报告，2008．

［4］Zhang Chuanbin，Tian Weifeng，Jin Zhihua．A novel method improving the alignment accuracy of a strapdown inertial navigation system on a stationary base［J］．Measurement Science And Technology，2004，15:756-769．

［5］I Clay Thompson，Jr，Kenneth S Morgan．Rapid self-alignment of a strapdown inertial system through real-time reprocessing［P］．US，US7739045，2006-5-31．

［6］Kenneth S Morgan，I Clay Thompson，Jr．High speed gyrocompass alignment via multiple Kalman filter based hypothesis testing［P］．US，US7512493，2006-5-31．

［7］Goshen-Meskin D，Bar-Itzhack I Y．Observability analysis of piece-wise constantsystem-partI:Theory［J］． IEEE Transactions on Aerospace and Electronics Systems，1992，28（4）:1056-1067．

［8］付梦印，邓志红，闫莉萍．Kalman滤波理论及其在导航系统中的应用（第二版）［M］．北京:科学出版社，2010．

［9］David H Tittertion，John L Weston．Strapdown inertial navigation technology（2ndEdition） ［M］．United Kingdom:The Institution of Electrical Engineers，2004．

［10］秦永元，张洪钺，汪叔华．卡尔曼滤波与组合导航原理［M］．西安:西北工业大学出版社，1998．