如何提高课尾小结的有效性

周峰

摘要：目前，很多课尾小结往往是老师主讲，草草了事，或者是虚假民主，求全求美的情景，使得小结毫无“生气”，学生毫无“灵气”，犹如最后的奄奄一息，下课前的最后哀声。如何提高课尾小结的有效性，个人认为应注意下三点：课尾的领跑点、助跑点、兴奋点。

关键词：课尾小结；领跑点；助跑点；兴奋点；有效性

中图分类号：G623.5文献标识码：A 文章编号：1992-7711（2015）10-060-1

郑毓信教授在《国际视角下的小学数学教育》一书中指出：“数学教学的基本目的，应是帮助学生通过数学学习学会用新的不同观点去看待世界，包括从更高的层面对已有生活经验和学习（探究）经验作出反思和必要的更新，以及在数学上得到新的发展。”这一主张说明教师应多引导学生学会反思，学会从从更高层面对已经历的学习过程做出新的反思或更新。

一、课尾小结的领跑点

课堂上老师要舍得花时间引导学生去小结。一个学生对数学学习思路清不清楚，与学生会不会主动参与课尾小结与反思有着很大的关系，因此，课堂中教师尽可能地保证时间让学生去观察总结反思，为发挥小结的作用提供保障。也许学生的思考与总结不够“完善”，你一言、我一语的发言不够全面，甚至一些学生说不到“点子”上而影响一堂课的“完美结局”，但这毕竟是属于学生自己的“成果”，是学生自主建构知识的结果，从发展学生的认知结构而言，显然更具有积极意义。课尾小结的领跑点应是学生而不是老师，小结应是学生的自我构建，而非教师或个别学生代劳。

二、课尾小结的助跑点

1.知识的梳理，助力学生知识体系的自我构建

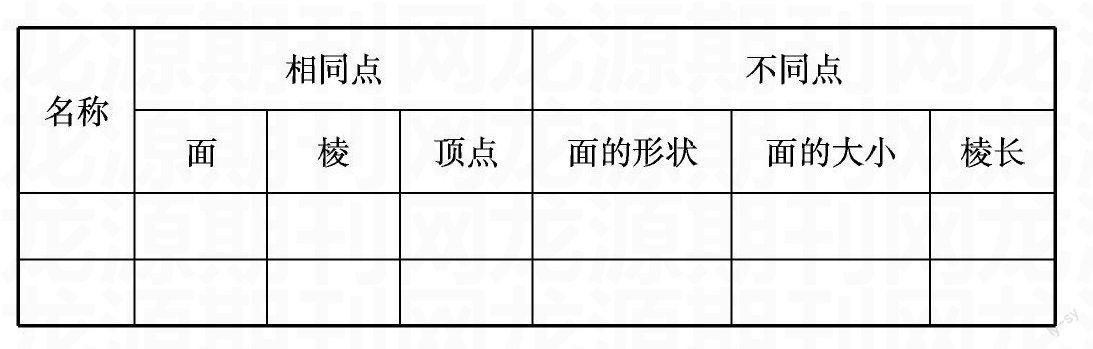
课尾小结应是对前面“学”的一种梳理，帮助学生从总体上把握知识，培养学生归纳总结、表达的能力，特别是尝试用自己的语言表述，经过学生的思考、发言、交流，这样对知识的掌握会有更深刻的理解，另外，还要注重与相关知识体系的构建，加强比较和区分，这样对所学知识就更容易“储存”，也更容易“提取”。如：学习了长方体和正方体的认识后，可以按面、棱、顶点的次序，归纳总结完成下表：

名称相同点

面棱顶点不同点

面的形状面的大小棱长

再譬如在学习了“最大公约数、最小公倍数”后，教师既要对此内容进行概括小结，还要联系“约数和倍数的意义、素数和合数”等进行连贯性归纳，使学生对此有更整体的认识和掌握。

2.过程的回顾，助力学生数学思想和方法的提炼

数学思想和方法不同于一般数学知识，它呈现的方式是隐蔽的，需要靠平时的点滴“渗透”，实践表明，长期坚持对学习历程的回顾与总结，对于学生领悟数学思想和方法都是十分有效的。

如：苏教版五年级上册《解决问题的策略 一一列举》课尾小结时，我们要让学生回顾刚才成功的经验是什么，怎样找就更容易找全了。反复的重温分类讨论、列举的过程，让学生不断地体验“分类”这种数学思想方法。

又如《平行四边形的面积》课尾小结时，我们让学生回顾平行四边形的面积公式推导过程，可以让学生画图演绎、也可以文字表述、还可以图文结合。最后小结交流时，让学生对照图或文自我介绍，反复让学生说，回顾和重温转化、演绎的过程，让学生不断地体验“转化和演绎”这两种数学思想方法。

3.悬念的延伸，助力学生探索未知兴趣的提升

在课尾提出一些启发性、趣味性或是暗示新的学习内容的一些问题，不仅可以使新旧知识有机地联系起来，形成连贯性，更能使学生带着问题、带着思考和探索未知的兴趣走出课堂，把课堂延伸至课外及下一堂课。

如《圆柱、圆锥的表面积和体积复习课》课尾小时，还可以提出：“圆柱的表面积和体积我们已会解决了，圆锥的体积也没问题了，但是（停顿一会儿）圆锥的表面积呢？有表面积吗？那又该如何解决呢？”

又如《乘法分配律的意义》课尾小结时，还可以加入：“前面学了乘法交换律和结合律，我们发现利用它们可以使有些计算变简便，今天我们也认识和理解了乘法分配律的意义，那它对于有些计算能否简便呢？能的话，又该如何正确使用呢？”

三、课尾小结的兴奋点

临近课堂尾声，学生已较疲劳，注意力和兴奋度也明显下降，那该如何激发学习的兴奋点，使学生身心得到放松，浓厚的学习兴趣得到保持呢？笔者觉得课尾小结应注意以下几个方面：

1.趣味性。课尾小结中注意寓教于乐，使小结与游戏、故事、口诀（或歌谣）等学生喜闻乐见的形式紧密结合，这样可以淡化课尾的疲劳感，激发学生的学习兴趣。

2.生活化。生活是数学的宝库，生活中随处都可以找到数学的原型，在小结时，教师应经常让学生联系实际生活学习数学，引导学生用数学的眼光找出生活中的数学问题，这样，不仅有利于培养学生用数学的眼光认识周围事物的习惯，而且有利于调动学生的学习热情。

3.差异化。人人学有价值的数学，不同的人在数学上得到不同的发展。每个班的学生都会有不同的差异，若只有统一的要求，势必会造成一部分学生觉得要求较低、乏味无趣或者一部分学生觉得要求较高、不知所云、难以企及。所以一般可以分为这三类：“学到了哪些知识”这种“陈述性”的小结作为必答题，“应该注意些什么”这类小结和“提炼出数学思想方法等”这类深层次的“反思性”的小结作为附加题或选答题，三类问题也可以让学生根据自己的情况选做。