基于L1/2正则项的磁共振图像稀疏重构
2015-07-07马杰葛岭岭苑焕朝张婷婷
马杰,葛岭岭,苑焕朝,张婷婷
(河北工业大学电子信息工程学院,天津 300401)
基于L1/2正则项的磁共振图像稀疏重构
马杰,葛岭岭,苑焕朝,张婷婷
(河北工业大学电子信息工程学院,天津 300401)
磁共振图像可以利用压缩感知从数量非常有限的观测数据集合中重构出,然而为了能够做到这一点,必须要解决定义在大量数据集合上的非光滑函数的最小化这一困难问题.通常L1范数能够产生稀疏解,但它往往与真实稀疏解(L0的解)差距甚大.针对该问题,研究一种基于变量分裂的图像重构模型,引入待重构图像的L1/2范数作为新正则项,采用交替增广拉格朗日乘子法进行求解.为考察方法的稳定性和重构效果,结合不同参数等评价标准与现有的图像重构模型进行比较.实验结果表明,L1/2范数作为正则子的图像重构模型相对于原有模型,图像重构结果稳定性好,可以获得更高的信噪比.
磁共振;压缩感知;L1范数;L1/2范数;变量分裂
压缩感知[1](CS)是Donoho和Candes等提出的一种新兴的信号获取与处理理论.如果图像在某个变换域可以稀疏表示,那么可以通过求解相关的优化问题,就可由随机采样的稀疏系数来进行重构,并在一定程度上保持原有图像的重构质量.核磁共振成像(简称NMRI),也称磁共振成像(MagneticResonanceImaging,简称MRI),是利用核磁共振原理,绘制物体内部的结构图像.傅里叶变换法是最基本的MRI重建方法之一,但由于该方法运算量大,重建速度慢,实际中很少采用这种方法.基于压缩感知的MRI重构算法利用MRI稀疏表示或局部光滑的先验知识,通过求解相应的优化问题来实现图像重构.目前已有多种算法解决此类优化问题,例如Trzasko等提出SL0算法[2](smooth L0norm),它利用图像小波变换域稀疏性,用光滑L0范数近似L0范数重构图像,有效解决了范数优化中的NP难问题,Bhaskar提出当0<p<1时基于Lp范数的迭代加权最小二乘(iterativelyreweightedleastsquare,IRLS)算法[3],实验证明了基于Lp范数优化算法在重构信号效果及可靠性方面优于L1及L0范数优化算法,Bioucas-Dias等提出TVMM(Total variation based majorization minimization)算法[4],该算法利用图像局部光滑特性,采用全变分正则化重构图像.文献[5]采用非线性共轭梯度下降算法求解加权范数最小化问题,在迭代过程中,根据所求得的图像稀疏表示来更新权值矩阵,增强MR图像的稀疏性,提高了图像的重建质量.四川大学的李青[6]提出了一种基于压缩感知的自适应正则化MRI重建算法,该方法结合了图像稀疏性和图像局部光滑性的先验知识,在非线性共轭梯度下降算法的基础上,同时自适应地改变局部正则化参数,实验证明该算法可以较好地恢复图像边缘.研究中发现,当采样数逐渐减少时,上述算法重构效果都不是很理想,重构的图像也不稳定.针对这一问题,徐宗本院士[7]等提出尝试引用L1/2范数作为新的正则项求解,通过仿真实验表明,所提出的基于变量分裂的图像重构新模型提高了待重构图像的稳定性,在采样数减少的情况下也能很好的重构出图像.
1 MRI图像重构模型及解法
1.1 图像重构的基本模型
磁共振成像技术是一种对人体无损伤的体外影像检查手段,可以获得组织和器官的解剖结构、生理功能和病变信息.磁共振扫描的速度是磁共振成像在许多应用中的一大瓶颈,缓慢的扫描速度导致运动伪影的产生,也给动态成像带来了困难.缩短原始数据采集时间,减少采样数据,不仅可以提高效率、减少病患的不适,还是实现心血管检查、功能信息获取等动态成像的关键所在.由于MRI信号可以通过TV模型、频域模型和字典模型等方法进行稀疏变换将信号转换为稀疏信号,故MRI图像本身具有稀疏性,因此MRI图像重构构成压缩传感理论应用的重要分支.利用压缩传感理论,可以极大减少对MRI图像Fourier域的采样数目.研究发现,目前的磁共振图像重建算法大多是基于的凸优化问题的求解,虽然基于的凸优化算法是极其有效的,但它们进行重建所需的观测值与理论最小值的差距甚大,特别是在采样数少的情况下,不能高效稳定的重构出原始图像,针对这一问题需要新的改进方法.
图像重构属于图像处理范畴中的逆问题,其模型表示如下

但是L0问题为NP组合难问题,对较大规模数据无法直接求解.针对这一问题,研究者们提出了一系列寻找次优解的贪婪算法:匹配追踪算法,正交匹配追踪算法[9]等.但是贪婪算法时间代价过高,无法保证收敛到全局最优.为使求解稀疏性问题变得可行,需要寻找合适的范数近似求解上述优化问题,当前一般性的作法是将L0范数最小化问题松弛到L1范数最小化问题[10],从而将一个组合优化问题松弛到一个凸优化问题来求解.即
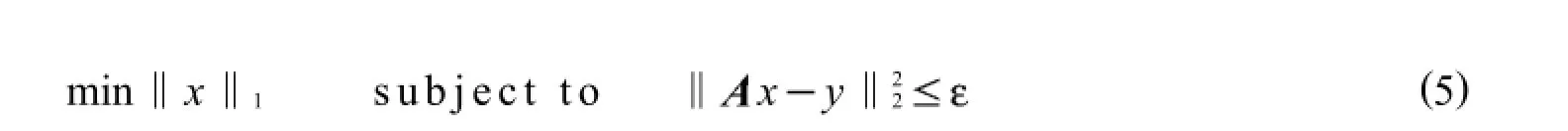
1.2 基于交替增广拉格朗日乘子法的算法
对于式(5)求解已经存在很多算法,其中基追踪BP[11]算法是最早提出的一种算方法,该算法在每次迭代时寻求最匹配的原子,文献[12]提出的凸集投影POCS算法在两个凸平面上进行交替投影来实现图像的重构.文献[13]提出一种简单的迭代收缩算法IST,只要确定步长值和阈值就可求解,但该算法收敛速度慢.文献[14,15]提出一种两步迭代收缩算法TwIST,该算法在每次迭代时,不像IST算法利用前一次的估计值,而是寻找新的估计值,新的估计值取决于前两次的估计值,但收敛速度也不够快.快速阈值收缩算法[16]FIST是对基于梯度的光滑凸优化问题的Nesterov优化算法的非光滑变形,虽然在时间上有所提高,但是还不能到达理想效果,文献[17]提出一种针对稀疏结构的稀疏重构算法SpaRSA,实验表明该算法的重构效果明显高于IST算法,但运行时间有待提高.
增广拉格朗日乘子法[18](ALM)相对与其他算法,重构时间
快而且可以达到更高的精度,ALM的优化模型如下


表1 ALM算法Tab.1ALM algorithm
ALM算法的流程图如表1所示.
迭代过程中,当目标函数的相对变化低于停止阈值时迭代停止,默认的停止阈值为0.01.
与ALM算法相比,在交替最小化方法[19]的基础上提出的交替增广拉格朗日乘子法(ADMM)[20],其最大的优越性在于将原问题分解为若干个更容易得到全局解的交替的极小化子问题,充分利用了目标函数的可分离性.利用ADMM方法,Afonso[21]等提出了一种基于变量分裂法的图像复原算法(SALSA算法)

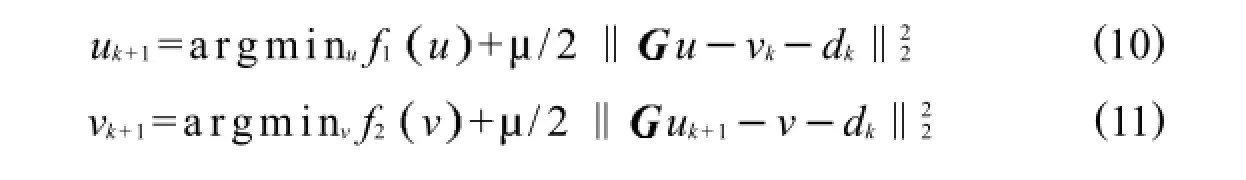
2 改进的MRI稀疏磁共振图像重构方法
2.1 L1/2正则化
研究中发现:L1求解框架不能保证获得满意的稀疏解,它往往与真实稀疏解(L0的解)差距甚大[7].并且当采样数逐渐减少时,L1求解框架重构效果不理想,对于含有重尾分布的误差数据往往不能取得较好的效果,重构的图像也不稳定.因此一个自然改进方法是使用Lq框架(0<q<1),但是Lq是非凸问题,理论分析与求解都非常困难.对于这一问题,徐宗本[6]等人根据空间理论得到启示.
1/p+1/q=1在对偶框架下,LP1p形成一个以L2为中心的局部凸空间体系.在p+q=1的对偶框架下,Lq0q1会形成一个以为中心的非局部凸空间体系,L1/2应该有特殊性.从图1单位球的形状可以看出,L1/2正则子所产生的解会比L1正则子产生的解更具有稀疏性.
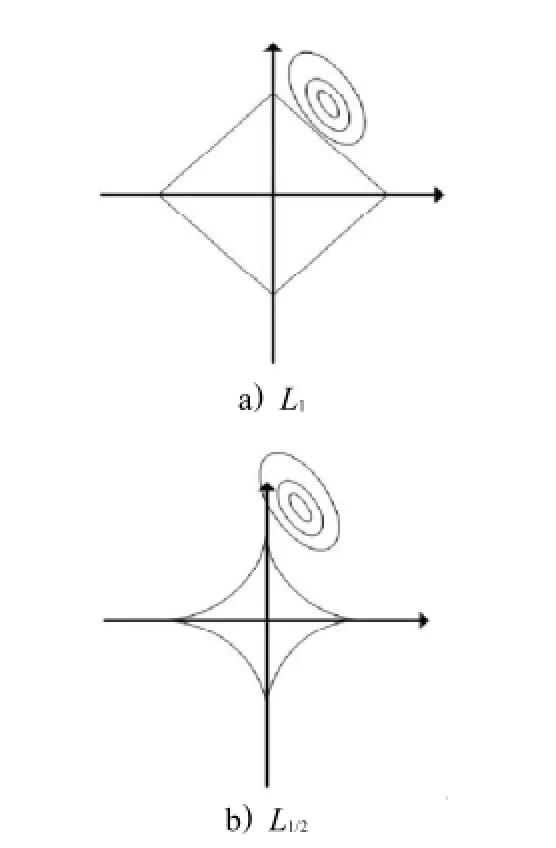
图1 不同正则子产生稀疏解得示意图Fig.1Different from L1/2regularizationand L1regularizations
根据徐宗本院士的基本思想,研究一种改进的图像重构模型,惩罚项中将L1换成L1/2,即

2.2 MRI稀疏磁共振图像重构的改进模型

根据推导过程,求解流程如表2所示.
本文的重构算法中将停止阈值设定为5×106.
如果式(16)和式(17)有准确解,根据Eckstein-Bertsekas定理[22]可保证此算法的收敛性.
定理1Eckstein-Bertsekas定理
式(8)的非约束优化形式为
表2 基于正则项的磁共振图像重构算法Tab.2Magnetic resonance image reconstruction algorithm based on1/2regularization

表2 基于正则项的磁共振图像重构算法Tab.2Magnetic resonance image reconstruction algorithm based on1/2regularization
No算法1 set k=0,choose>0,v0,d02 repeat 3xk+1=argminx1/2‖Ax y‖22+/2‖x vkdk‖22 4 dk+1=dkHzk+1b 5vk+1=argminv‖v‖1/21/2+/2‖xk+1v dk‖22 6 kk+1 7 until stopping criterion is satisfied

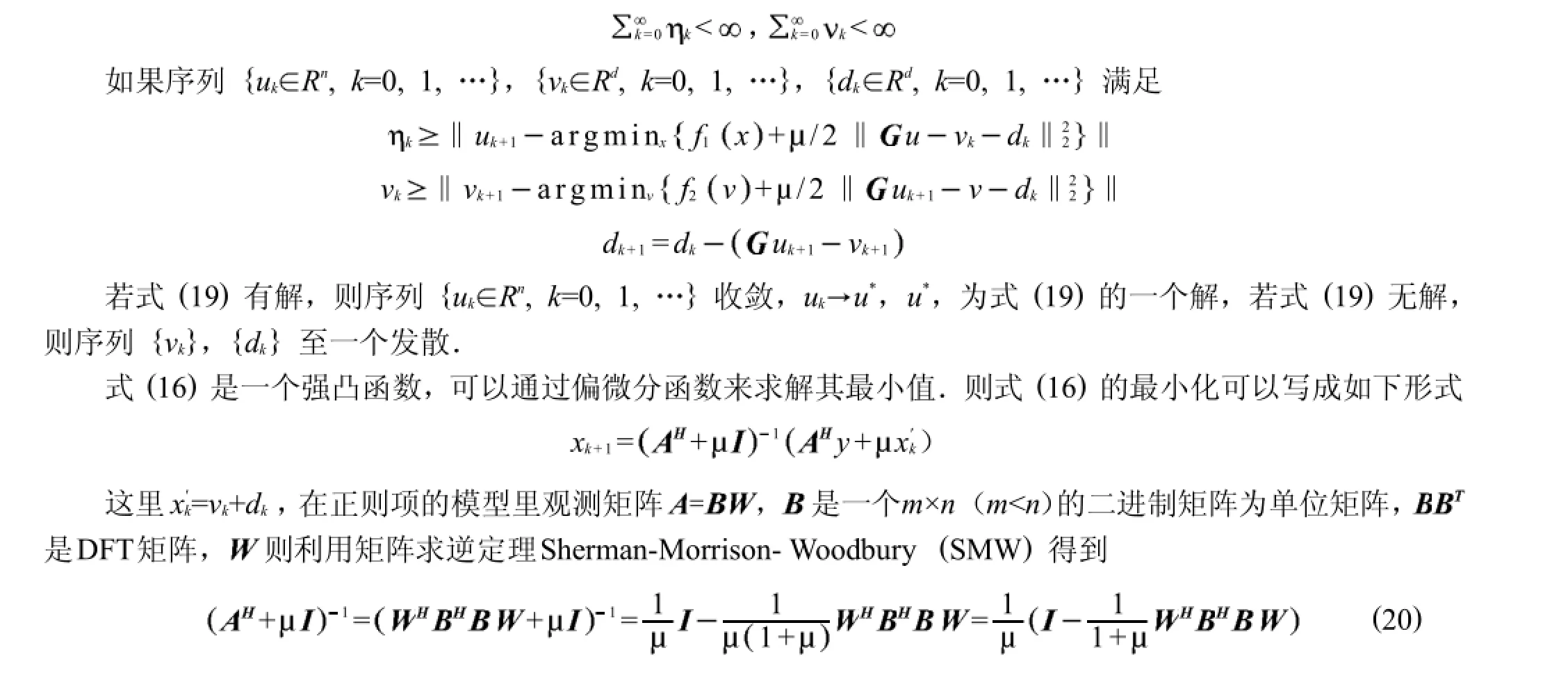

3 实验结果与分析
3.1 评价标准
为验证本文方法的有效性,采用Shepp-Logan脑部模型的磁共振图像进行验证,在实验中采样模式有好多种,例如非笛卡尔采样、径向采样、螺旋采样、变密度采样等,但非笛卡尔采样具有采样速度快、对流动不敏感等优点,它在脑功能成像、心脏冠状动脉成像等方面得到了人们的关注,故本文采用非笛卡尔辐射状采样,在脑部模型的Fourier频谱表示图上,均匀取L条射线,然后在每条射线上高斯采样.并且根据CSMRI理论要求可知,对k空间进行的欠采样要满足是随机的,即采样模式要满足变换点分布函数不相关性,除了本文采用的非笛卡尔采样外,其他几种采样模式通常都满足不相关欠采样的性质,因此,本方法在其他采样模式下依然适用.现利用CPU为2.0GHz,内存为2G的计算机,通过MATLAB进行编码.本文分别通过以下几个参数对改进的模型与L1范数的进行分析比较.
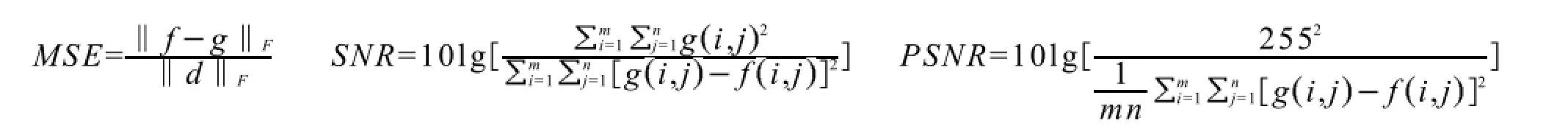
式中:g为原始图像;f为重构图像;d为含噪图像;m和n为图像的维数;MSE代表差错率.从上式可以看出重构出的图像与原始图像越接近,则‖fg‖F就越接近零,那么差错率就越小.SNR与PSNR分别代表信噪比和峰值信噪比,SNR与PSNR越大说明重构出来的图像越逼近原始图像.
3.2 不同模型的比较
将正则项分别是范数L1和L1/2范数的实验结果进行比较,L1范数的求解方法采用软阈值方法,实验结果如表3所示,运用两种方法,在不用分辨率与采样数的情况下,计算出原始图像和重构图像的相对误差,以及算法的迭代数和运行时间.从仿真结果表3中可以看出,当分辨率较低时,虽然改进模型在重构时间上较L1模型慢,但是准确度较高,随着分辨率的增加改进模型的重构速度明显高于原来的L1模型,当分辨率为256×256,采样数为52时,改进模型的重构时间是55.14s,L1模型的重构时间是184.97 s,改进模型的重构速度比原来L1模型的速度高出3倍.在采样数减少的情况下,改进的模型的准确度明显高于L1的模型,其相对误差至少高出一个百分点,改进的模型在采样射线为22时重构出的图像的差错率是9.02×10-7,L1的模型在采样射线为52时的差错率是2.38×10-6,两种模型的差错率相近.
图2给出在分辨率为32×32情况下,当采样数不同时改进模型和L1模型差错率的对比图,从图中可以看出采样数越少,改进的模型重构图像的效果较于L1模型重构的效果越好,当采样射线减少到22时,改进的模型重构图像的准确度比L1模型高出大约4个百分点,与采样数为52时重构图像的准确度相近.图3给出在分辨率为128×128情况下两种方法差错率的对比图,与图2进行比较可以看出,当分辨率增加时,L1模型重构的准确度有了一定程度的下降,改进模型基本没有太大的波动,说明改进模型重构图像的稳定性要高于原来的L1模型.
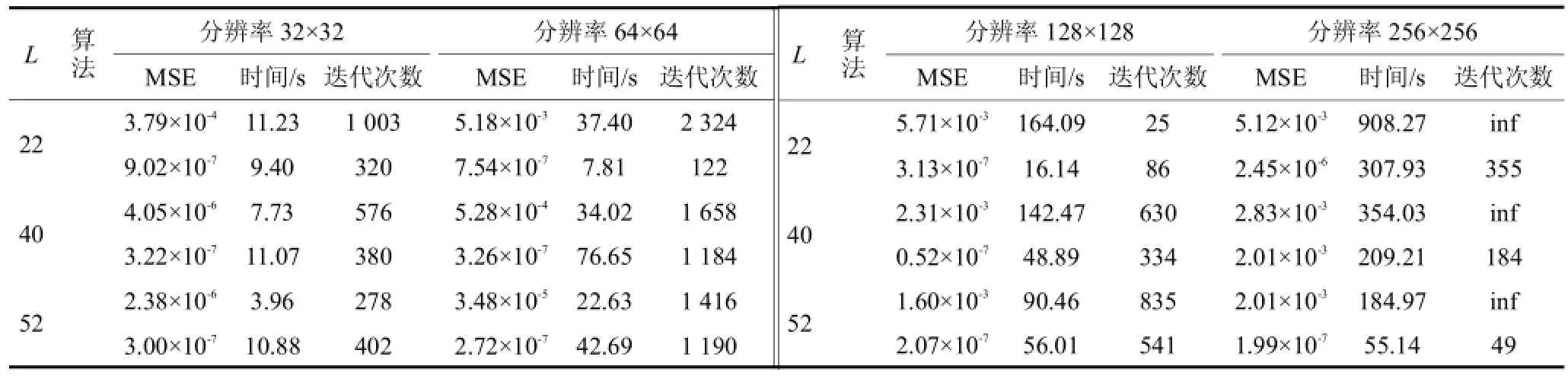
表3 不同正则化方法随不同采样数的图像恢复结果Tab.3Image restoration results from different regularizations with different sampling number

图3 两种方法在恢复差错率上的对比(128×128)Fig.3 Comparisonoftwomethodsintherecoveryerrorrate(128×128)
图4是两种算法恢复效果的PSNR和SNR,从图中可以看出改进的模型有很大的优势,在采样数为22时,改进模型的SNR是48 bB,L1模型是23 dB,比L1模型高出25 dB,改进模型的PSNR是119 dB,L1模型是100 dB,比L1模型高出19 dB.图5给出重构时间的对比图,可以看出改进模型在重构时间上有了很大的提高,尤其是采样数少的情况下,改进模型的重构时间是16.14 s,L1模型重构时间是164.09s.图5和图6分别是MRIscan图像的原始图像和分辨率为64×64,采样数为52的Fourier频谱图.图7和图8分别是L1模型和改进模型在采样数为52的情况下的重构结果,可以看出L1模型只是重构出图像的大致轮廓,差错率为3.48×10-5,而改进模型重构的差错率是2.72×10-7,重构效果高于原来的L1模型2个百分点.

图4 两种方法在PSNR与SNR上的对比(128×128)Fig.4Comparison of two methods in PSNR and SNR(128×128)

图5 两种方法在运行时间上的比较(128×128)Fig.5Comparison of two methods in PSNR and SNR(128×128)
图6 原始图像Fig.6The original image

图7 采样数为52的Fourier频谱图Fig.7The Fourier spectrum with the sampling number 52
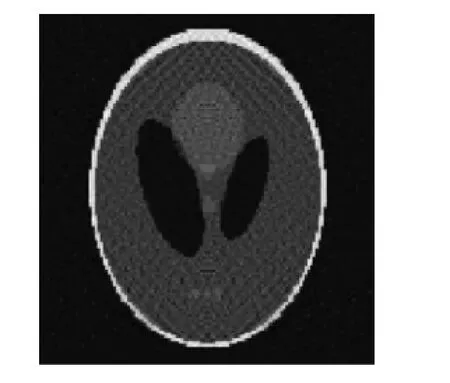
图8 模型重构结果Fig.8Model reconstruction result

图9 改进模型重构结果Fig.9Improved model reconstruction result
4 结论
本文研究了一种磁共振图像重构的新方法,可以稳定有效地从稀疏采样中重构原图像,该模型选取L1/2范数作为正则项,解决了L1范数作为正则项时重构图像不稳定和稀疏度较差的问题,为磁共振图像重构方法提供了新的思路.由实验结果可以看出,该模型可以有效对稀疏磁共振图像进行重构,重构效果明显高于原来的模型,恢复时间以及信噪比都有了很大的提高,并且差错率有了明显的下降.数据实验表明在采样数减少的情况下,本文的方法可以有效重构出图像,增强了图像重构的稳定性,提高了重构图像的信噪比并且降低了重构图像的差错率,达到高信噪比低差错率的理想效果.
[1]BLUMENSATHT.Compressedsensingwithnonlinearobservationsandrelatednonlinear optimizationproblem[J].IEEEtransactionsonInformation theory[J].2013,59(6):3466.
[2]PENGX,ZHANGM,ZHANGJ,etal.AnalternativerecoveryalgorithmbasedonSL0formultibandsignal[C]//Instrumenta-tionandMeasurement Technology Conference(I2MTC),2013 IEEE International.IEEE,2013:114-117.
[3]BHASKAR D RAO,KENNETH KREUTZ-DELGADO.An affine scaling methodology for best basis selection[J].IEEE Transactions on signal processing,1999,47(1):1.
[4]BIOUCAS-DIAS J M,FIGUEIREDO M A T,Oliveira J P.Total variation based image deconvolution:a majorization minimization approach C// Toulouse:IEEE Conference,2006,2:278-281.
[5]李红,杨晓梅,李青.基于加权压缩感知的MR图像重建方法[J].中国组织工程研究与临床康复,2012,16(26):4817-4821.
[6]李青,杨晓梅,李红.基于压缩感知的自适应正则化磁共振图像重建[J].计算机应用,2012,32(2):541-544.
[7]XU ZONGBE,CHANG XIANGYU,XU FENGMINe.L-1/2 Regularization:A thresholding representation theory and a fast solver[J].IEEE Transactions on neural net-works and learning systems,2012,23(7):1013-1027.
[8]CANDES EJ,ROMBERR J.Robust UncertaintyPrinciples:Exact signal reconstructionfrom highly iIncomplete frequencyinformation[J].IEEE Transaction on Information Theory,2006,52(2):489-509.
[9]TROPP J A,GILBERT A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):465-466.
[10]CANDES E J,WAKIN M.An Introduction to compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30.
[11]HE W,QU T.Audio lossless coding/decoding method using basis pursuit algorithm[C]//Acoustics,Speech and Signal Processing(ICASSP),2013 IEEE International Conference on.IEEE,2013:552-555.
[12]PIRES R G,PEREIRA L A M,MANSANO A F,et al.A hybrid image restoration algorithm based on projections onto convex sets and harmony search[C]//Circuits and Systems(ISCAS),2013 IEEE International Symposium on.IEEE,2013:2824-2827.
[13]MA Z.Sparse principal component analysis and iterative thresholding[J].The Annals of Statistics,2013,41(2):772-801.
[14]BIOUCAS-DIASJM,MARIOATFIUEIREDO.ANewTwIST:Two-stepiterativeshrinkage/thresholdingalgorithmsforimagerestoration[J].IEEE Transactions on Image processi processing,2007,16(12):2992-3994.
[15]BIOUCAS-DIAS J M,MARIO A T FIUEIREDO.Two-step algorithms for linear inverse problem with non-quadratic regularization proceeding of ICIP[J].IEEE International Conference on Image Processing,2007(1):I-105-I-108.
[16]MENG X,DUAN S F,MA S X.An adaptive regularized fast iterative shrinkage-thresholding algorithm for image reconstruction in compressed sensing[J].Advanced Materials Research,2013,710:593-597.
[17]WRIGHTS,NOWAKR,FIUEIREDOM.Sparsereconstructionbyseparableapproximation[J].IEEETransactiononSignalProcessing,2009,57:2479-2493.
[18]LIN Z C,CHEN M M,MA Y.The augmented lagrange multiplier method for exact recovery of a corrupted low-rank matrix[EB/OL].http:// arxiv.org/abs/1009.5055.2013.
[19]JAIN P,NETRAPALLI P,SANGHAVI S.Low-rank matrix completionusing alternating minimization[C]//Proceedings of theforty-fifth annual ACM symposium on Theory of computing.ACM,2013:665-674.
[20]STEPHEN BOYD,NEAL PARIKH.Distributed optimization and statistical learning via the alternating direction method of multipliers[R].Foundation and Trends in Machine Learning,2010,3(1):1-122.
[21]AFONSO M,BIOUCAS-DIAS J,FIUEIREDO M.An augmented lagrangian approach to the constrained optimization formulation of imaging inverse problems[J].IEEE Transactions on Image Processing,2011,20(3):681-695.
[22]AFONSOM,BIOUCAS-DIAS J,FIUEIREDOM.Fastimagerecoveryusingvariablesplittingandconstrainedoptimization[J].IEEE Transactions on Image Processing,2010,19(9):2345-2356.
[责任编辑 代俊秋]
Sparse MRI reconstruction based on L1/2regularization
MA Jie,GE Lingling,YUAN Huanchao,ZHANG Tingting
(School of Electronic Information Engineering,Hebei University of Technology,Tianjin 300401,China)
Magnetic resonance images can be reconstructed close to the original in which we use the compressed sensing from a very limited number of observation data set.However,to achieve this,we must solve a problem:the nonsmooth functions that definition in the data set to minimize.Usually the norm can produce a sparse solution,but it is different from the true sparse solution(solution).To solve the problem,a method is proposed based on variable splitting image reconstruction model.The method is introduced the norm as a new regular of the reconstructed images,which was solved by alternating theaugmentedLagrange multipliermethod.Finally,to verifythe stability andreconstructioneffect,selecting different parameters and evaluation standard are compared with existing models ofimage reconstruction.The experiments indicate that the improved model has excellent stability and gets a higher signal-to-noise ratio.
magnetic resonance imaging;compressed sensing;L1norm;L1/2norm;variable splitting
TP391.9
A
1007-2373(2015)04-0001-08
10.14081/j.cnki.hgdxb.2015.04.001
2014-12-22
国家自然科学基金(61203245);河北省自然科学基金(F2012202027)
马杰(1978-),男(回族),副教授.
数字出版日期:2015-06-30
数字出版网址:http://www.cnki.net/kcms/detail/13.1208.T.20150630.1615.001.html
